Восстановите порядок действий при решении задачи составление уравнения (6 видео)

Порядок выполнения действий, правила, примеры

Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.

В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.

Содержание

Порядок вычисления простых выражений
Что такое действия первой и второй ступени
Порядок вычислений в выражениях со скобками
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Решение задач составлением уравнения
Алгебра. 8 класс
🔍 Видео

Видео:Математика 6 класс (Урок№51 - Решение задач с помощью уравнений. Часть 1.)Скачать

Порядок вычисления простых выражений

В случае выражений без скобок порядок действий определяется однозначно:

Все действия выполняются слева направо.
В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Условие: вычислите, сколько будет 7 − 3 + 6 .

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7 − 3 + 6 = 4 + 6 = 10

Ответ: 7 − 3 + 6 = 10 .

Условие: в каком порядке нужно выполнять вычисления в выражении 6 : 2 · 8 : 3 ?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Условие: подсчитайте, сколько будет 17 − 5 · 6 : 3 − 2 + 4 : 2 .

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:

17 − 5 · 6 : 3 − 2 + 4 : 2 = 17 − 10 − 2 + 2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7

Ответ: 17 − 5 · 6 : 3 − 2 + 4 : 2 = 7 .

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

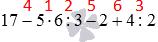
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Видео:Уравнение. Практическая часть - решение задачи. 1 часть. 5 класс.Скачать

Что такое действия первой и второй ступени

Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).

Видео:Математика 6 класс. Решение задач на составление уравненийСкачать

Порядок вычислений в выражениях со скобками

Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:

Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.

Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.

Условие: вычислите, сколько будет 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 .

Решение

В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7 :

7 − 2 · 3 = 7 − 6 = 1

Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 5 + 1 · 2 : 2

Начнем с умножения и деления, потом выполним вычитание и получим:

5 + 1 · 2 : 2 = 5 + 2 : 2 = 5 + 1 = 6

На этом вычисления можно закончить.

Ответ: 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 6 .

Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.

Условие: вычислите, сколько будет 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) .

Решение

У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · ( 2 + 3 ) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .

Ответ: 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) = 28 .

Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.

Допустим, нам надо найти, сколько будет ( 4 + ( 4 + ( 4 − 6 : 2 ) ) − 1 ) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6 : 2 = 4 − 3 = 1 , исходное выражение можно записать как ( 4 + ( 4 + 1 ) − 1 ) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению ( 4 + 5 − 1 ) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .

Видео:8 класс. ОВР. Окислительно-восстановительные реакции.Скачать

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.

Разберем пример такого вычисления.

Условие: найдите, сколько будет ( 3 + 1 ) · 2 + 6 2 : 3 − 7 .

Решение

У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид ( 3 + 1 ) · 2 + 36 : 3 − 7 .

Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.

( 3 + 1 ) · 2 + 36 : 3 − 7 = 4 · 2 + 36 : 3 − 7 = 8 + 12 − 7 = 13

Ответ: ( 3 + 1 ) · 2 + 6 2 : 3 − 7 = 13 .

В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.

Видео:Алгебра 8. Урок 12 - Задачи на составление дробно-рациональных уравнений (Часть 1)Скачать

Решение задач составлением уравнения

Разделы: Математика

«Умственную самодеятельность, сообразительность и смекалку нельзя ни «вдолбить», ни «вложить» ни в чью голову. Результаты надёжны лишь тогда, когда введение в область математических знаний осуществляется в лёгкой и приятной форме, на предметах и примерах обыденной и повседневной обстановки, подобранных с надлежащим остроумием и занимательностью».

Е.И. Игнатьев «В царстве смекалки»

Цель обучающая: Научить анализировать условие задачи, выбирать рациональные способы решения, составлять уравнение, решать его, проверять правильность решения.

Цель воспитательная: Развитие абстрактного и логического мышления.

I. Актуализация опорных знаний.

1) Что называется уравнением? Что называется корнем уравнения? Что значит решить уравнение?

2) Решите уравнение .

Решение: а) ; ; x= ;

б) НОЗ=6; ; ; ; ;

3) Составьте буквенное выражение.

Наташа купила блокнот за m рублей, книгу на 20 рублей дороже блокнота и ручку в 2.5 раза дешевле книги. Сколько рублей стоит ручка?

Решение: (m+20) рублей цена книги, рублей цена ручки.

4) Из двух сёл, расстояние между которыми 10 км навстречу друг другу вышли мальчик и девочка и встретились через 2 часа. Скорость мальчика 3 км/час. Найдите скорость девочки.

Решение: а) 3*2=6(км) прошел мальчик, 10-6=4(км) прошла девочка, 4:2=2(км/ч) скорость девочки

б) 10:2=5(км/ч) скорость сближения, 5-3=2(км/ч) скорость девочки.

II. Сообщение темы и цели урока.

III. Решение задач составлением уравнения.

1) Андрей старше Олега на 4 года, а Олег старше Бориса в 1,5 раза. Вместе им 36 лет. Сколько лет каждому из них?

Первый ряд решает задачу, взяв за неизвестную величину возраст Андрея, второй ряд — возраст Олега, третий ряд-возраст Бориса. А затем каждый ряд объясняет своё решение у доски.

Условие задачи	Решение уравнения	Проверка
Х лет Андрею, лет Борису,		16+12+8=36
Х лет Олегу лет Борису		12+16+8=36
Х лет Борису (1,5х+4) лет Андрею		8+12+16=36

Если в задаче несколько неизвестных величин, лучше обозначить буквой наименьшую из них.

2) Два пешехода вышли одновременно навстречу друг другу из двух посёлков и встретились через 3ч. Расстояние между посёлками 30 км. Найдите скорость каждого пешехода, если у одного она на 2 км/ч меньше, чем у другого.

а) Ученики решают задачу составлением уравнения.

Х км/ч – скорость 1-го пешехода

(х+2) км/ч – скорость 2-го пешехода

3х км прошел 1-й пешеход

3(х+2) км прошел 2-й пешеход

3х+3(х+2)=30	4
3х+3х+6=30	+6
6х+6=30	+12
6х=24	+18
Х=4	=30

б) Затем решают арифметическим способом.

10-2=8(км/ч)-две скорости 1-го пешехода.

8:2=4(км/ч)-скорость 1-го пешехода.

4+2=6(км/ч)-скорость 2-го пешехода.

Вывод. Арифметическое решение задачи более рациональное

3)Для распечатки 340 страниц были использованы две копировальные машины. Первая машина работала 10 минут, а вторая 15 минут. Сколько страниц в минуту печатает каждая машина, если первая печатает на 4 страницы больше, чем вторая?

Снова дети решают задачу алгебраически и арифметически.

А) х страниц за 1 минуту печатает 2-я машина,

(х+4) страниц за 1 минуту напечатает 1-я машина,

15х страниц напечатает 2 машина,

10(х+4) страниц напечатает 2 машина,

15х+10(х+4=340	12
15х+10х+40=340	+16
25х+40=340	+180
25х=300	+160
Х=12	=340

б) 10*4=40(стр) на столько страниц больше напечатает 1-я машина за 10 минут

340-40=300(стр) напечатали бы обе машины вместе, если бы у них были одинаковые скорости.

10+15=25(мин) работали обе машины.

300:25=12(стр) за 1-у минуту печатает 2-я машина.

12+4=16 (стр) за 1-у минуту печатает 1-я машина.

При решении задач с помощью уравнения поступают следующим образом:

Внимательно читают условие задачи.
Обозначают неизвестную величину буквой.
Переводят условие задачи на алгебраический язык.
Составляют уравнение.
Решают уравнение.
Проверяют правильность решения

V. Домашнее задание.

Решить задачу алгебраически и арифметически.

Охотничья собака спугнула зайца, который сидел под кустом в 150м от неё. Через сколько минут собака догонит зайца, если она пробегает за 6 минут 3,6км, а заяц только 3км?

Л.В. Кузнецова, Е.А. Бунимович, Б.П. Пигарев, С.Б. Суворова «Алгебра» сборник заданий для проведения письменного экзамена по алгебре за курс основной школы. Москва. «Дрофа». 2001г; стр 43, работа №31, вариант 1(5); стр 50, работа №38, вариант 2(7); стр 65, работа №48, вариант 1(6).
Составители Т.А. Братусь, Н.А. Жарковская, Е.А Рисс, Т.Е Савелова «Детский математический календарь 2001-2002». Санкт — Питербург стр10.
Н.Т. Кострикина «Задачи повышенной трудности в курсе алгебры 7-9 классов». Москва. «Просвещение» 1991 стр5-19.

Видео:Решение задач с помощью уравнений. Видеоурок 29. Математика 6 классСкачать

Алгебра. 8 класс

Впишите верный ответ.

Одна труба наполняет бассейн на 2 часа быстрее, чем вторая труба. За сколько часов бассейн наполнится через первую трубу, если известно, что через обе трубы бассейн наполняется за 2 часа 24 минуты?

Укажите правильный ответ.

Моторная лодка прошла 36 км против течения и 22 км по течению, затратив на весь путь 3 часа. Найдите скорость течения реки, если собственная скорость лодки 20 км/ч.

Укажите все правильные ответы.

Выберите возможные уравнения для решения задачи.
Числитель обыкновенной дроби меньше её знаменателя на 1. Если к числителю прибавить 2, а к знаменателю – 5, то она уменьшится на 0,2. Найдите эту дробь.