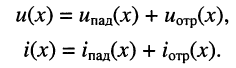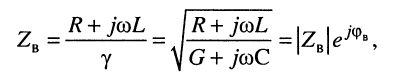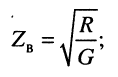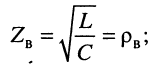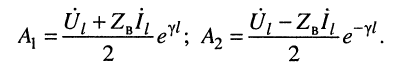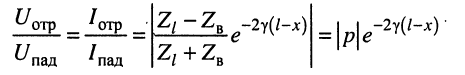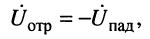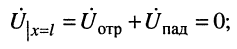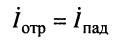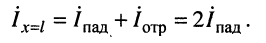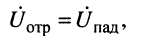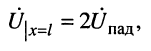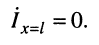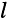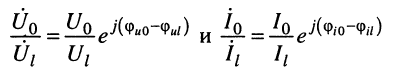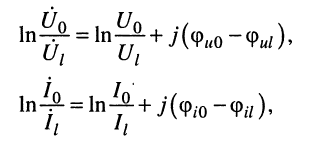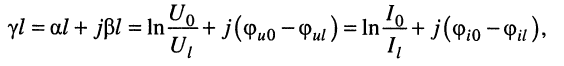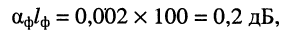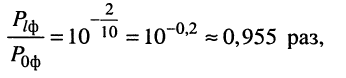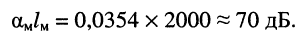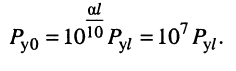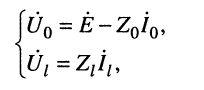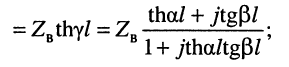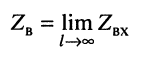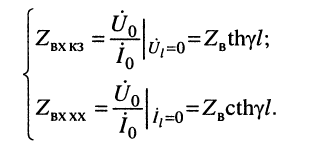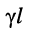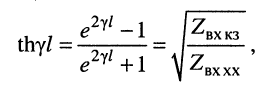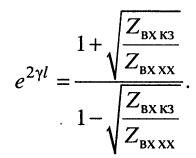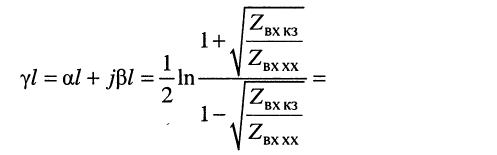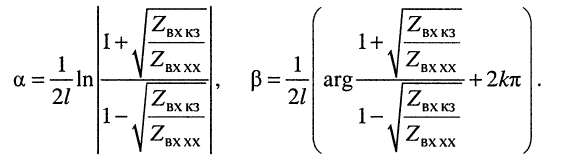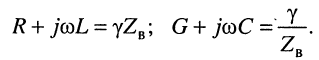Однородные и неоднородные волновые уравнения для векторов ЭМП. Уравнения Даламбера. Решение однородных уравнений Даламбера. Сферическая волна. Волновой фронт. Волновые уравнения Гельмгольца.
Плоские волны как частные решения волновых уравнений. Плоская волна как предельный случай сферической волны. Решения волновых уравнений для гармонических полей в виде плоских и сферических волн.
Плоские ЭМВ в однородной изотропной среде. Отличие понятий «волна» и «колебание». Свойства плоской волны, структура и ориентация векторов ЭМП. Коэффициенты фазы и ослабления. Длина волны. Фазовая скорость, скорость распространения энергии, групповая скорость.
Характеристическое и волновое сопротивления. Ослабление ЭМВ, глубина проникновения ЭМП в вещество.
Указания к теме
Решением волновых уравнений являются функции координат и времени, которые описывают ЭМВ, распространяющиеся в свободном пространстве, направляющих системах и других устройствах. Необходимо получить четкое представление о таких понятиях, как фазовая поверхность (волновой фронт) и ее форма, однородная и неоднородная волна, затухающая волна.
Следует выучить определения длины волны, коэффициентов затухания и фазы, групповой и фазовой скоростей, волнового и характеристического сопротивлений, глубины проникновения ЭМВ в вещество.
Основные сведения
Для анализа распространяющихся ЭМВ из системы уравнений Максвелла в дифференциальной форме целесообразно вывести уравнения, которые зависят либо только от 
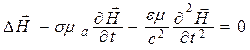
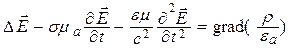
Как показали расчеты и эксперименты, константа с ( 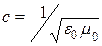
Уравнения (5.1) и (5.2) называют волновыми уравнениями Ж. Д’Аламбера [5, 12]. Если правая часть равна нулю, то уравнение называют однородным, а если нет – неоднородным. При отсутствии электрических зарядов (r = 0) уравнения (5.1) и (5.2) практически совпадают, что подтверждает равноправие векторов 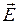
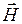
Несмотря на кажущуюся независимость уравнений (5.1) и (5.2), следует помнить о том, что у переменного ЭМП векторы 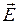
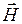
Волновые уравнения в комплексной форме имеют вид
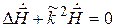
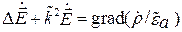
где 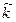
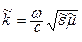
Уравнения (5.3) называют волновыми уравнениями Г. Гельмгольца. При отсутствии потерь проводимости (s = 0) исчезают вторые слагаемые в уравнениях (5.1) и (5.2), а также в (5.3)–(5.4) возможно упрощение:
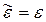
Рассмотренные уравнения называются волновыми потому, что их решениями являются волны и, в частности, ЭМВ.
Фазовым фронтом волны называют поверхность, проходящую через точки с одинаковыми фазами, по форме этой поверхности определяется название волны (сфера – сферическая ЭМВ, плоскость – плоская и т. д.) [1–3].
Решение однородного волнового уравнения для плоских волн
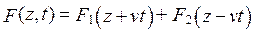
Каждое из слагаемых выражения (5.5) описывает возмущения F1 и F2, исходящие из точки z0 в момент t = 0 и к моменту времени t приходящие в точку z = z0 – vt для F1 и в точку z = z0 + vt для F2 со скоростью v [1].
Для сферических волн решение волнового уравнения имеет вид:
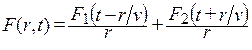
Первое слагаемое выражения (5.6) представляет собой сферическую волну, расходящуюся от источника. Второе слагаемое часто отбрасывают, поскольку волна, движущаяся внутрь источника, обычно не рассматривается [1].
В отличие от выражения (5.5) амплитуда сферической волны (5.6) уменьшается при удалении от источника как 1/r (мощность – как 1/r 2 ), что связано с тем, что мощность изотропного источника распределяется по расходящимся сферам (4.10).
Таким образом, даже при отсутствии потерь в пространстве плотность потока мощности сферической волны уменьшается с расстоянием как 1/r 2 .
На большом расстоянии от источника ЭМВ (в дальней зоне антенны) сферический волновой фронт в области приемной антенны можно аппроксимировать плоскостью, подобно тому, как земную поверхность считают плоской при малых высотах и на дистанциях, много меньших расстояния прямой видимости.
Плоская ЭМВ – идеализированная волна, имеющая плоский фазовый фронт (z = const), у которой существуют две взаимно перпендикулярные составляющие 
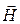
В дальнейшем будем считать, что направление распространения ЭМВ совпадает с осью z. Уравнения Максвелла в комплексной форме для составляющих векторов плоской волны в ДСК имеют вид
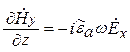
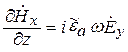
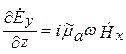
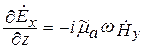
Из формул (5.7) следует, что 
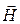
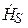
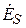
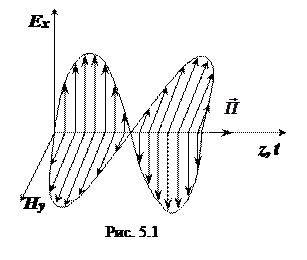
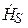
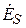
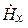
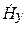
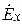
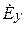
Вектор Пойнтинга в данном случае имеет только продольную составляющую 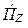
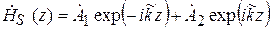
Первое слагаемое выражения (5.8) соответствует прямой волне, второе слагаемое – обратная волна, 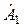
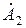

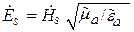
Запишем связь волнового числа ( 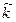
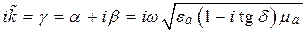
Уравнение плоской волны с учетом (5.10) можно записать в виде
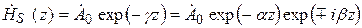
Для мгновенных значений из выражения (5.11) получаем
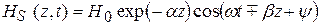
Направление распространения ЭМВ можно определить из анализа зависимости полной фазы (5.12) 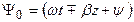
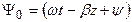
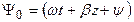
Из анализа формул (5.10)–(5.12) очевидно, что a– это коэффициент затухания, а b – коэффициент фазы.
Подставляя формулу (5.12) в (5.1), после решения уравнений относительно a и b получаем
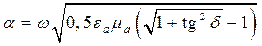
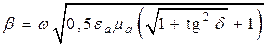
Множитель 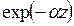
Ослаблением (A) ЭМВ по полю называют величину (AP = A 2 – ослабление ЭМВ по мощности)
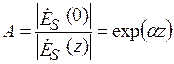
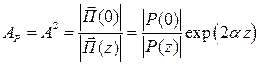
На практике часто используют ослабление в децибелах (дБ):
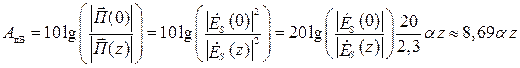
С ослаблением непосредственно связана глубина проникновения ЭМП в вещество (D° ), называемая также толщиной поверхностного слоя (скин-слоя, но это понятие логичнее использовать для металлов):
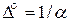
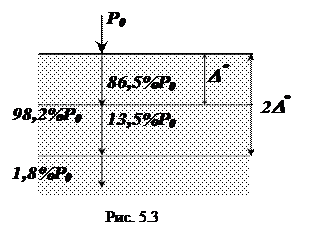
Таким образом, зная коэффициент затухания, можно определить область преимущественной концентрации энергии ЭМВ в веществе.
В случае диэлектриков толщина поверхностного слоя значительна, в то время как для проводников на ВЧ и ОВЧ она составляет доли миллиметра [1].
Параметры ЭМВ. Длиной волны l называется расстояние между двумя фронтами ЭМВ, различающимися по фазе на 2p (360°):
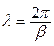
Фазовой скоростью vф называется скорость перемещения фазового (волнового) фронта ЭМВ. При анализе выражения (5.12) ранее были определены направление движения и скорость фронта ЭМВ
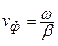
Фазовая скорость может изменяться в любых пределах (может быть больше с!), поскольку не является скоростью переноса энергии [1].
Групповой скоростью vгр называют скорость движения фронта (например, максимума) огибающеймодулированного сигнала.
Информационный сигнал не является монохроматическим, он занимает полосу частот. Каждая спектральная составляющая может иметь свою скорость распространения, что в диспергирующих средах приводит к искажениям сигнала.
Понятие «групповая скорость» вводится для сред с малыми потерями, поэтому при Dw vф ( 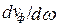
При Dw/w0 ® 0 период огибающей стремится в бесконечность, понятие «группа волн» распространяется на весь сигнал, и в итогеvгр ® vЭ.
Групповая скорость узкополосного сигнала – это скорость передачи энергии, она не может быть выше скорости света.
Характеристическое сопротивление (Zс) [41] ЭМВ равно отношению амплитуд поперечных составляющих электрического и магнитного полей
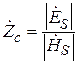

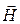

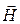

Определим характеристическое сопротивление плоской волны. Пусть 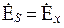
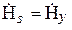
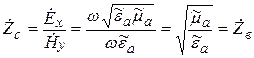
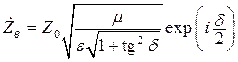
Получается, что характеристическое сопротивление [41]зависит только от параметров среды. Zв называют волновым сопротивлением среды. Следует отметить, что стандартом [41] рекомендуется термин «характеристическое сопротивление». Для ЭМВ, распространяющейся в некоторой среде, Zc = Zв.
Волновое сопротивление вакуума Z0 (s = 0, e = m = 1) :
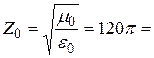
Тогда выражение (5.22) можно записать в виде
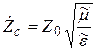
Список рекомендуемой литературы:[1, гл. 6–7, с. 30–38; 2, с. 50–56; 3, гл. 6–7, с. 27–34; 4, с. 26–33; 5, с. 26–30; 6, с. 116–123, 128–142, 198–205; 7, с. 67–82, 250–259; 8, с. 62–68; 9, с. 69–74; 10, с. 68–73; 11, с. 67–69, 130–139; 12, с. 182–194; 13, с. 140–149, 174–177, 187–190; 15, с. 302–307].
Контрольные вопросы и задания
1. Почему рассматриваемые в этой теме уравнения называются волновыми?
2. Чем волна отличается от колебания?
3. Чем отличаются волновые уравнения Д’Аламбера и Гельмгольца?
4. Следует ли из волновых уравнений независимость электрической и магнитной составляющих ЭМП?
5. Можно ли считать свет ЭМ волной?
6. Какие упрощения возможны в волновых уравнениях для сред без потерь?
7. Можно ли по виду электрической или магнитной составляющей плоской ЭМВ определить расположение другой составляющей ЭМП и направление распространения ЭМВ?
8. При каких условиях волновые уравнения для векторов 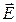
9. Каково простейшее решение системы уравнений Максвелла?
10. Дайте определение волнового фронта.
11. Почему плотность потока энергии сферической волны уменьшается при удалении от источника даже в пространстве без потерь?
12. Какие упрощения в анализе ЭМП дает понятие «плоская волна»? В каких практических случаях допустимо ЭМВ считать плоской?
13. Чем отличаются однородные и неоднородные плоские волны?
14. Дайте определение коэффициентам затухания и фазы плоской ЭМВ.
15. Чем отличается волновое число k от g ?
16. Какова пространственная структура плоской ЭМВ?
17. Как определить направление распространения ЭМВ?
18. Как с помощью понятия толщины поверхностного слоя можно оценить область преимущественной концентрации ЭМП?
19. Дайте определение основным характеристикам ЭМВ.
20. Чем групповая скорость отличается от фазовой?
21. Может ли фазовая скорость иметь бесконечное значение?
22. Чем волновое сопротивление отличается от характеристического?
23. Является ли групповая скорость скоростью передачи энергии?
24. Что такое дисперсия? Приведите примеры дисперсионных сред.
25. Укажите условие неискаженной передачи сигнала.
26. Чем нормальная дисперсия отличается от аномальной?
- Физика волновых процессов
- Плоские электромагнитные волны в поглощающей среде. Скорость волны. Глубина проникновения. Поверхностный импеданс металлов. Скин-слой. Поток мощности.
- В однородной среде луч – прямая линия. При переходе границы раздела между двумя различными средами луч меняет направление. Соединим лучом точку р1(0,у1) в среде с показателем преломления n1 с точкой р2(а,у2) в среде с показателем преломления n2. Луч пересекает границу раздела в точке (х,0). Полное время распространения света от р1 до р2 равно t = . Используя условие стационарности , получаем: . Учитывая, что , , где q – угол между направлением луча и нормалью к границе раздела, имеем: n1sinq1 = n2sinq2 – закон преломления.
- Волновые параметры длинной линии
- Соотношения между комплексными амплитудами падающих и отражённых волн
- Волновое сопротивление
- Коэффициент отражения
- Уравнения передачи согласованно нагруженной длинной линии
- Постоянная передачи и частотные характеристики длинной линии
- Частотные характеристики (АЧХ и ФЧХ) согласованно нагруженной длинной линии
- Входное сопротивление длинной линии
- Определение параметров линии методом холостого хода и короткого замыкания
- 🎥 Видео
Видео:2-0. Метод комплексных амплитудСкачать
Физика волновых процессов
ФИЗИКА ВОЛНОВЫХ ПРОЦЕССОВ
1. Волновое уравнение. Гармонические волны. Уравнение Гельмгольца. Фазовый фронт, фазовая скорость, длина волны. Стоячие волны. Неоднородные плоские волны. Цилиндрические и сферические волны.
2. Плоские электромагнитные волны в поглощающей среде. Глубина проникновения. Поток мощности. Скорость волны. Поверхностный импеданс металлов. Скин-слой.
3. Дисперсия волн. Волновой пакет. Фазовая и групповая скорости. Нормальная и аномальная дисперсии. Дисперсионное уравнение.
4. Прохождение плоской волны через границу раздела двух сред. Коэффициенты Френеля. Явление полного внутреннего отражения. Угол Брюстера. Приближенные граничные условия Леонтовича.
5. Плоские электромагнитные волны в анизотропных средах. Продольное и поперечное распространение в намагниченной плазме. Обыкновенная и необыкновенная волны. Эффекты Фарадея и Коттона-Мутона.
6. Излучение волн. Ближняя и дальняя зоны. Диаграмма направленности линейного излучателя. Понятие области мнимых углов. Излучение волн плоским раскрывом.
7. Электромагнитные волны в направляющих системах. ТЕ, ТМ и ТЕМ волны. Критическая частота. Длина волны в направляющей системе. Волновое сопротивление линии передачи.
8. Приближение геометрической оптики. Уравнение эйконала. Световые лучи. Область применимости лучевого приближения. Принцип Ферма. Рефракция.
Волновое уравнение. Гармонические волны. Уравнение Гельмгольца. Фазовый фронт, фазовая скорость, длина волны. Стоячие волны. Неоднородные плоские волны. Цилиндрические и сферические волны.
Зададим некоторое возмущение, распространяющееся в пространстве, в виде U=U(at–bs), где t – текущее время; s – пространственная координата, вдоль которой распространяется возмущение, и продифференцируем 2 раза по t и 2 раза по s:


сравнивая (1) и (2) и учитывая, что 

Перейдя к характеристическим переменным 


Здесь предполагается, что U изменяется только в одном направлении s, задаваемом единичным вектором m, тогда s = (mr) (r – радиус-вектор точки наблюдения). В некоторый момент времени t=to U() = const, если s = const. Т. к. (mr) = const – уравнение плоскости, то 
Если 

(приведенное волновое уравнение или уравнение Гельмгольца). Это уравнение описывает распространение гармонических свободных волн. Величина 





Если волна распространяется в направлении единичного вектора m, можем ввести вектор k = km (волновой вектор), тогда ks = (kr), и поверхность равных фаз ks = const определяется уравнением плоскости (kr) = const, нормальной к направлению распространения волны. Если k – вещественный вектор, то А=const всюду. Такая волна называется однородной плоской волной.
Функция F удовлетворяет однородному уравнению Гельмгольца и в том случае, если
k=k+ik но при условии, что |k|2 = k2 – вещественно, т. е. (kk) = 0, а |k|2–|k|2 = k2. В этом случае решение 
Для произвольной зависимости от координат однородное волновое уравнение имеет следующий вид 

В цилиндрических координатах 






В сферических координатах 




1. , , Сухоруков волн. — М.: Наука, 1979.
2. Вайнштейн волны. — М.: Радио и связь, 1988.
Видео:Билет №34 "Электромагнитные волны"Скачать

Плоские электромагнитные волны в поглощающей среде. Скорость волны. Глубина проникновения. Поверхностный импеданс металлов. Скин-слой. Поток мощности.
В средах с потерями (s ¹ 0) имеем: [ÑH] = iweE+sE = iw (e — is /w)E = iw




mотн= 4p10-7[Гн/м] ). Пусть в такой среде вдоль оси z распространяется плоская гармоническая волна, удовлетворяющая уравнениям: 







Здесь: a – коэффициент затухания, b – коэффициент фазы, Zo – волновое сопротивление среды

Таким образом, в поглощающей среде амплитуда уходящей волны убывает по экспоненциальному закону,
уменьшаясь в e раз на расстоянии d=1/a, которое называется глубина проникновения (скин-слой), длина волны l=2p/b и фазовая скорость vф=w /b уменьшаются по сравнению с непоглощающей средой, в среде с электрическими потерями Ну отстает по фазе от Еx на величину d /2 (в среде с магнитными потерями, когда комплексной величиной является m , Ну опережает Еx), поверхность равных фаз совпадает с поверхностью равных амплитуд. Для сред с tg d >>1 (металлы) 



В среде с потерями поток мощности через единицу поверхности П=[EH*] становится комплексным.
Мгновенное значение Пz равно
Пz=











 |
Компоненты поля в первой и во второй средах имеют вид:
2. Параллельно поляризованная волна
Поле падающей волны:
компоненты поля отраженной волны:
компоненты поля преломленной волны:

На границе раздела (у=0) для любых z должно выполняться
Нпадexp(-ik1zsinq) + Нотрexp(-ik1zsinq¢) = Нпрexp(-ik2zsiny),
Откуда следуют законы Снелиуса: sinq = sinq¢ и k1sinq = k2siny.
Учитывая Еt1= (НпадZ01+ НотрZ01)cosq и Еt2= НпрZ02cosy, запишем граничные условия для параллельно поляризованной волны в виде:



где Rêê и Têê – коэффициенты Френеля для параллельно поляризованной волны. (Rêê – коэффициент отражения, Têê – коэффициент прохождения). R2êê + T2êê= 1.


Компоненты поля в первой и во второй средах имеют вид:
Для диэлектриков m1= m2= m0, и коэффициенты Френеля можно записать в виде:

где 
Анализ этих выражений показывает, что для параллельно поляризованной волны существует угол падения qБ = p/2 – y, при котором R||=0. Этот угол, определяемый из соотношения tgqБ=
Из закона Снелиуса sin y = 


При падении волны из свободного пространства на границу раздела с хорошо проводящей средой, у которой tgd>>1, siny Þ 1, т. е. тангенциальные компоненты поля на поверхности проводника непрерывно переходят в поперечные компоненты поля уходящей вглубь проводника волны. Соотношение между ними можно записать в виде Еt=Zos[Htyo], где Zos – поверхностный импеданс проводящей среды, yo – орт нормали к границе раздела. Это импедансное граничное условие называют приближенным граничным условием Леонтовича.
1. , Зернов поля и волны. — М.: Сов. радио, 1971.
2. , Никольская и распространение радиоволн. М. Наука, 1989
Волны в анизотропных средах
Для изотропных сред, свойства которых не зависят от направления, B = mH и D = eE, где e и m — скалярные величины, следовательно: Bx= mHx, By=mHy, Bz=mHz, Dx= eEx, Dy=eEy, Dy=eEy. Существуют анизотропные среды, которые в разных направлениях имеют различные свойства, т. е. связь между проекциями векторов B и H или D и E описывается соотношениями
Bx= mxxHx+ mxyHy + mxzHz, By= myxHx+ myyHy + myzHz, Bz= mzxHx+ mzyHy + mzzHz, .
Dx= exxEx+ exyEy + exzEz, Dy= eyxEx+ eyyEy + eyzEz, Dz= ezxEx+ ezyEy + ezzEz, .
Формально эту связь принято представлять в виде 



В природе неизвестны вещества, у которых одновременно e и m имеют тензорный характер, поэтому в дальнейшем будем рассматривать вещества, обладающие или диэлектрической или магнитной анизотропией.
Типичными представителями анизотропных сред являются намагниченные плазма и феррит.
Плазма — электрически нейтральный газ, в котором значительная часть атомов или молекул ионизирована
Под действием электрического поля на каждый электрон действует сила Fk= –Eeo (кулоновское взаимодействие). Если движущийся со скоростью v электрон находится в постоянном магнитном поле Н=, на него действует сила Лоренца Fл = –eomo[vH=], вследствие чего электрон получает также вращательное движение. В этом случае уравнение движения электрона имеет вид: 





Продольное распространение плоской волны в намагниченной плазме
При продольном распространении (вдоль H=) 






ik


(k2–w2exmo)E0y= iw2bmoE0x, (k2–w2exmo) = ±w2bmo или k1,2 = w

Таким образом, получили два решения, следовательно в намагниченной плазме одновременно распространяются две волны с волновыми числами k1=w 




Ey1=E01sin(wt–k1z) поляризации левого Ex2=E02sin(wt–k2z) при ex=b, k2 Þ 0, поэтому ее



Hy1= –


Необыкновенная волна при w Þ wm исчезает вследствие резонансного поглощения (явление гиромагнитного резонанса). Полное поле можно представить в виде: Еx=Ex1+Ex2=2Eocos[0.5(k1–k2)z]cos[wt–0.5(k1–k2)z], Еy=Ey1+Ey2=2Eosin[0.5(k1–k2)z]cos[wt–0.5(k1–k2)z], в каждый момент времени Еx и Еy синфазны, угол наклона вектора Е относительно оси x: q = arctg(Ex/Ey) = 0.5(k1–k2)z, т. е. поле имеет линейную поляризацию, но плоскость поляризации медленно вращается при распространении волны. Это явление называется эффект Фарадея. Угол, на который поворачивается плоскость поляризации при прохождении волной единицы длины q! = 0.5(k1–k2), называется постоянная Фарадея. Среды, в которых наблюдается эффект Фарадея, называются гиротропными (вращающими). Этот эффект невзаимный, т. к. при изменении направления Н= меняет знак b. Поскольку Z01 ¹Z02, поле Н имеет эллиптическую поляризацию.
Поперечное распространение в намагниченной плазме
При поперечном распространении (вдоль оси х) 








kE0z = wmoH0y волна «не чувствует» постоянного магнитного поля и называется обыкновенной. Волновое сопротивление обыкновенной волны Zоб=


kH0z = w(ibE0x+ exE0y) E0x находится в квадратуре с E0y, т. е. вектор Ен вращается в плоскости x0y.







Аналогичные явления имеют место и при распространении волн в намагниченном феррите – веществе, обладающем магнитными свойствами ферромагнетиков (mотн=5¸10000) и электрическими свойствами диэлектриков (eотн=5¸20). В магнитном поле магнитная ось атома прецессирует вокруг направления поля Н=, вследствие чего магнитная проницаемость феррита становится тензором



Литература. , Зернов поля и волны. — М.: Сов. радио, 1971.
Излучение волн. Ближняя и дальняя зоны. Диаграмма направленности линейного излучателя. Понятие области мнимых углов. Излучение волн плоским раскрывом.
Излучение – процесс преобразования энергии источника в энергию свободных волн. Математически задача сводится к решению неоднородного волнового уравнения. В случае электромагнитных волн удобнее использовать векторные потенциалы: Ñ2Ae+ k2Ae = –j ст e, Ñ2Am+ k2Am = –j ст m, где Ae и Am– электрический и магнитный векторные потенциалы, j ст e и j ст m– объемные плотности электрических и магнитных сторонних токов, заданных в объеме Va. Используя метод функции Грина, запишем решение в виде:

где 



В зависимости от расстояния до точки наблюдения используются разные приближения:
а) при r >> r¢, дальняя зона (зона Фраунгофера) в показателе экспоненты используется первое приближение: r @ rо– r¢cosa. Минимальное значение rмин, (граница дальней зоны) начиная с которого можно пользоваться этим приближением, определяется из условия (r¢2sin2a)/2ro
выражение (1) имеет вид

При вычислении Е и Н по формулам (2) отбрасываются слагаемые, пропорциональные r–2 и r–3. Тогда Еq= – ik(ZоАqе+Аjм), Еj=–ik(ZоАjе+Аqм), Еr=0; Нj= Еq ¤ Zо, Нq= –Еj ¤ Zо, Нr=0; где Zо– волновое сопротивление среды;
Аq=Аxcosq cosj+Аycosq sinj +Аzsinq , Аj= –Аxsinj +Аycosj, Аr=Аxsinq cosj+Аysinq sinj + Аzcosq.
В общем случае поле в дальней зоне можно представить в виде: Е= Ео

При r l быстрее изменяется fc(q), поэтому рассмотрим зависимость множителя системы от скорости волны тока, определяемой значением b. Введем величину y=kcosq, имеющую смысл пространственной частоты (–¥ k, называется областью мнимых углов, т. к. при этом cosq>1. Видно, что уменьшение скорости волны тока приводит к смещению максимума ДН от нормали к оси излучателя. Если скорость волны тока меньше скорости света (b>k), большая часть энергии “излучается” в область мнимых углов, т. е. отсутствует в дальней зоне и находится вблизи излучателя.
Для синфазного излучателя Dq0,5=51оl / L, УБЛ=0.21.
Излучение волн плоским раскрывом (апертурой)
Пусть на прямоугольной площадке, расположенной в плоскости x,y задано распределение поверхностных токов Je, m(x¢, y¢). В дальней зоне 

Ej= –ik(ZoAeycosj– Amx cosqcosj)= 
является поверхность с заданным на ней распределением электромагнитного поля, например раскрыв рупорной антенны, то согласно принципу эквивалентных токов Je=[Hn], Jm= – [En]. В этом случае Jmx= Eаy, Jey= – Hаx= – Eаy/Zф (здесь Zф= Eаy/Hаx – сопротивление фронта волны, возбуждающей раскрыв) и выражения для полей имеют вид:
Таким образом, излученное поле является суперпозицией сферических волн, имеет в общем случае эллиптическую поляризацию и диаграмма направленности излучателя может быть представлена в виде произведения множителя элемента на множитель системы: f(q, j) = fэ (q, j)fc(q, j), где fэ (q) = 





1. , , Грудинская и распространение радиоволн. — М.:Сов. радио,1979.
Электромагнитные волны в направляющих системах. ТЕ, ТМ и ТЕМ волны. Критическая частота. Длина волны в направляющей системе. Волновое сопротивление линии передачи.
Плоские однородные волны – простейший тип волнового процесса. При наличии границ возникают неоднородные плоские волны, распространяющиеся вдоль этих границ, т. е. возникают плоские направляемые волны. Это делает возможным передачу энергии на большие расстояния с минимальными потерями. Варианты конструктивного исполнения направляющих систем (линий передачи) приведены на рисунке.
Будем считать эти системы продольно однородными (их свойства сохраняются в одном прямолинейном направлении, например, вдоль оси z). Свободные плоские гармонические волны, способные распространяться в направляющей системе, определяются из однородных уравнений Гельмгольца: Ñ2Е + k2E = 0, Ñ2H + k2H = 0. В отличие от плоской волны в неограниченном пространстве, в направляющих системах могут существовать неоднородные плоские волны, имеющие продольную составляющую поля Еz или Нz. Связь между продольными и поперечными составляющими поля определим, используя метод разделения переменных, т. е. полагая Е = Е^(x,y)×exp(±igz), H = H^(x,y)×exp(±igz). Здесь g – продольное волновое число, определяющее скорость распространения волны вдоль z. Для поперечных компонент поля имеем Ñ2Е^+ (k2– g2) E^= 0, Ñ2Н^+ (k2– g2) Н^= 0, где (k2– g2) = c2 – поперечное волновое число, k2 = w2em, e и m – параметры среды, заполняющей линию передачи. Используя координатную запись однородных уравнений Максвелла относительно комплексных амплитуд Е и Н, имеем:



rot E = –iwmH 


в векторной форме имеем:

поперечные – ТЕМ или Т волны (отсутствуют продольные составляющие поля),
электрические – ТМ или Е волны (имеется продольная составляющая электрического поля),
магнитные – ТЕ или Н волны (имеется продольная составляющая магнитного поля),
гибридные – ЕН волны (имеется продольные составляющие электрического и магнитного поля).
Критическая частота: для волн Е и Н типа из c2 = (k2– g2) следует, что 
exp(–igz), т. е. амплитуда волны, распространяющейся вдоль z остается постоянной и меняется только фаза. Если c > k, то g – мнимая величина, следовательно, постоянной остается фаза и по экспоненте убывает амплитуда. При g= 0 имеем: c = k = 2pfкр 



Для ТЕМ волн (Еz =0 и Нz = 0) c2= 0, следовательно, g = k и fкр= 0, т. е. передача энергии возможна на всех частотах, включая нулевую (постоянный ток).
Волновое сопротивление линий передачи определяется исходя из следующих соображений:
используя систему уравнений, связывающих продольные и поперечные составляющие поля, получаем
для Е(ТМ) волн (Нz=0): 




Для Н(ТЕ) волн (Еz=0): 










изменение n на длине волны должно быть > Ñ2A – это условие связано с кривизной поверхности равных амплитуд rА и может быть записано в виде 2pnrA/l >>l/2pnA2, т. е. радиус кривизны ПРА, отнесенный к l, должен быть >> l. Чтобы пренебречь дифракционными явлениями размер фронта волны D должен быть >> l/n. Эти условия не выполняются в точках, где пересекаются лучи (фокус оптических систем); в средах с резкими неоднородностями; в мутных средах; при прохождении поверхностей с поглощающими экранами и т. д.
В неоднородной среде луч, соединяющий две точки р1 и р2, является кривой линией. Для каждой точки луча имеем: dL= (grad L×dr)=| grad L||dr|=k0n(r)dl, где dr направлен по лучу, dl – элемент длины пути. Изменение фазы вдоль луча равно 



В однородной среде луч – прямая линия. При переходе границы раздела между двумя различными средами луч меняет направление. Соединим лучом точку р1(0,у1) в среде с показателем преломления n1 с точкой р2(а,у2) в среде с показателем преломления n2. Луч пересекает границу раздела в точке (х,0). Полное время распространения света от р1 до р2 равно t =  . Используя условие стационарности
. Используя условие стационарности  , получаем:
, получаем:  . Учитывая, что
. Учитывая, что  ,
,  , где q – угол между направлением луча и нормалью к границе раздела, имеем: n1sinq1 = n2sinq2 – закон преломления.
, где q – угол между направлением луча и нормалью к границе раздела, имеем: n1sinq1 = n2sinq2 – закон преломления.



Для нормального состояния атмосферы 


В зависимости от состояния атмосферы различают следующие типы рефракции:
а) 
г) 
д) 
Видео:Билет №47 "Метод комплексных амплитуд"Скачать

Волновые параметры длинной линии
Содержание:
Волновые параметры длинной линии:
Полученные в предыдущей лекции уравнения передачи длинной линии (23.8) описывают комплексные амплитуды напряжения
Тогда для мгновенных значений напряжений и токов в линии получаем:
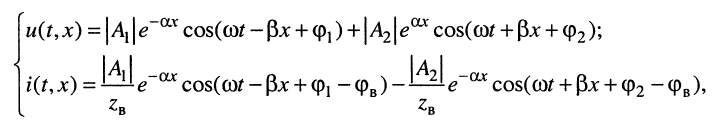
где 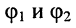
Решения (24.1) подтверждают, что напряжения и токи в длинной.линии являются функциями как времени 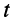
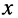
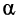
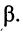
напряжений и токов, которые назовём падающими волнами напряжения и тока (смысл такого названия будет ясен из дальнейшего):
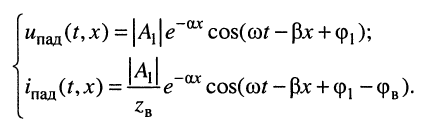
Из этих выражений следует:
- при любом фиксированном
т. е. в любом сечении линии, и напряжение
и ток
являются гармоническими колебаниями;
- амплитуды колебаний убывают по мере удаления от начала к концу линии по экспоненциальному закону
- в любом сечении линии отношение амплитуды напряжения
к амплитуде тока
равно модулю волнового сопротивления
а разность фаз между ними равна аргументу
волнового сопротивления линии;
- колебание напряжения
или тока
в сечении
отстаёт по фазе от колебания и
или
поскольку коэффициент фазы является величиной положительной:
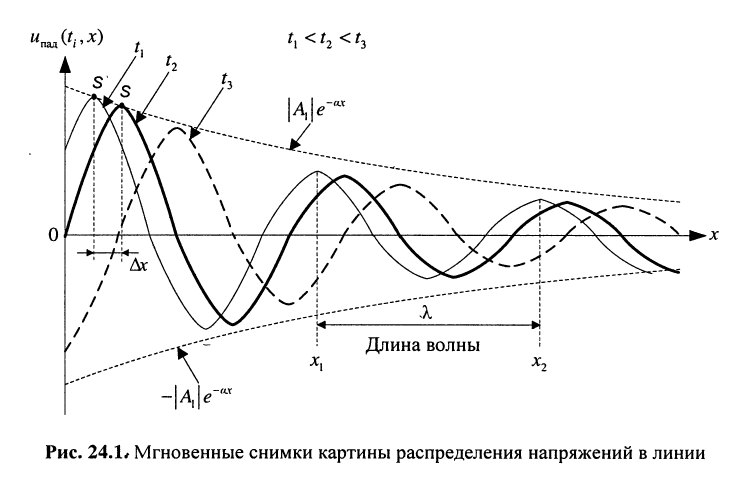
Сказанное демонстрируется на рис. 24.1, где представлено графическое распределение мгновенных значений напряжений 
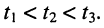
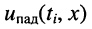
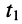
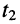
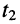
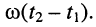
Определение:
Совокупность волн напряжения 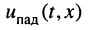
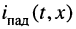
Найдём длину 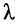
Под длиной волны понимают расстояние между смежными сечениями линии, фаза колебаний волны на которых отличается на 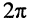
откуда имеем равенство
из которого получаем формулу для вычисления длины волны:
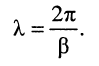
Определение:
Скоростью распространения, или фазовой скоростью, называют скорость 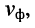
Нуль напряжения достигается в точках, где функция косинуса равна нулю, поэтому условие состояния равной фазы можно записать в виде равенства:
при этом аргумент имеет значения:
Продифференцировав обе части полученного равенства по переменной t, найдём скорость распространения нуля
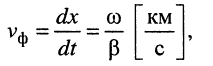
т. е. скорость распространения состояния равной фазы.
Фазовая скорость показывает, какое расстояние 
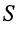
Рассмотрим, чему будет равен коэффициент фазы в наиболее характерной для практики области частот, когда 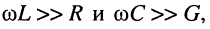
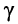
Разложение в ряды полученных в правой части биномиальных сомножителей и удержание в разложениях лишь по два слагаемых даёт:
Раскрывая скобки и пренебрегая в произведении величиной второго порядка малости, получаем приближённое выражение для коэффициента распространения:
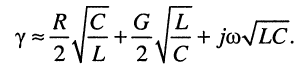
В линиях с хорошим диэлектриком проводимость чрезвычайно мала, поэтому второе вещественное слагаемое в выражении (24.5) оказывается очень малым по сравнению с первым, что позволяет записать формулы для коэффициентов затухания и фазы с хорошей степенью приближения:
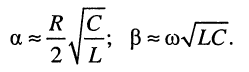
Тогда в указанной выше области частот фазовая скорость (24.4) согласно (24.6) оказывается равной
Подставляя сюда формулы значений первичных параметров длинной линии L и С (табл. 23.1), получаем:
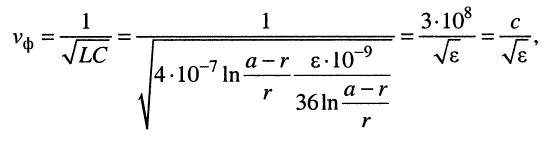
где с — скорость света.
Из (24.7) ясно, что для воздушных линий 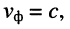
Интересно, что в области низких частот значение фазовой скорости убывает с уменьшением частоты. Это объясняется меньшим проявлением скин-эффекта: волна больше проникает в проводник, и колеблющиеся частицы внутри проводника возбуждают вторичные волны. Поскольку частицы обладают некоторой инерцией, образуемые ими вторичные волны запаздывают по фазе относительно вынуждающей колебания волны, поэтому происходит запаздывание фазы результирующей волны и, как следствие, уменьшение фазовой скорости.
Обратимся теперь ко вторым слагаемым уравнений (24.1), которые назовём отражёнными волнами напряжения и тока:
Проведя анализ этих слагаемых подобно тому, как это сделано для падающих волн, нетрудно убедиться, что они описывают затухающую волну такого же характера, как и падающая, но распространяющуюся в обратном направлении: от конца к началу линии.
Определение:
Волна напряжения 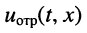
Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Соотношения между комплексными амплитудами падающих и отражённых волн
Из анализа, выполненного в разд. 24.1, следует:
- фазовая скорость отражённой волны совпадает с точностью до знака с фазовой скоростью падающей волны
- амплитуда напряжения (тока) отражённой волны максимальна в конце амплитуда напряжения (тока) падающей волны минимальна в конце линии;
- напряжение
(ток) в любой точке длинной линии
х является суммой напряжений (токов) падающей и отражённой волн:
Переходя к комплексным амплитудам напряжений и токов падающей и отражённой волн, входящих в уравнения передачи длинной линии (23.8), последние суммы для любого сечения линии можно записать в виде:
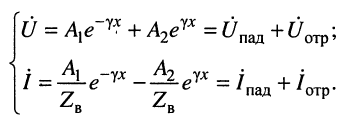
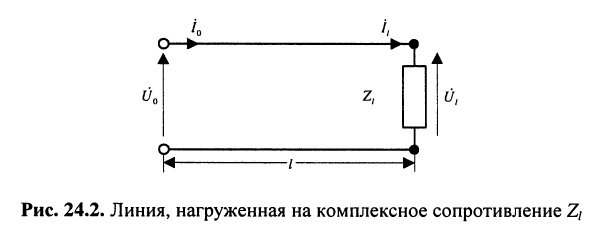
Практический интерес представляют соотношения между комплексными амплитудами падающих и отражённых волн в линии, имеющей длину 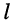
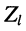
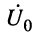
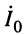
Волновое сопротивление
Прежде всего отметим, что при любом jc, т. е. в любой точке линии согласно (24.9) справедливы равенства:
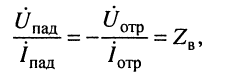
которое говорит о том, что в любом сечении линии .отношение комплексных амплитуд напряжения и тока падающей (отражённой) волны равно волновому сопротивлению линии
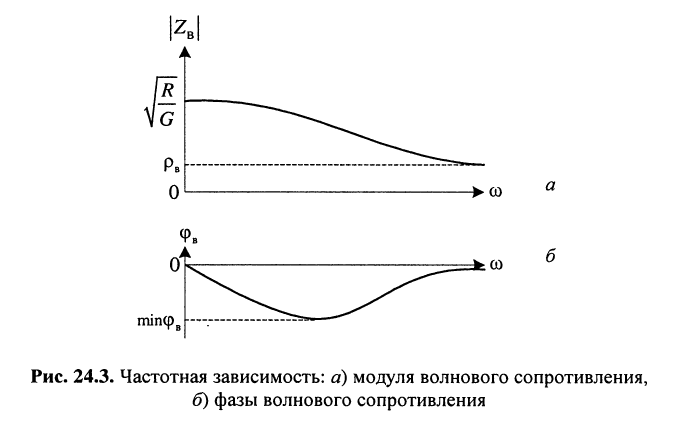
Свойства волнового сопротивления можно определить из выражений (24.10) и (23.6):
из которых следует:
модуль волнового сопротивления 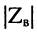
фаза (угол) 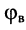
на частоте 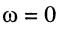
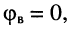
при стремлении частоты к бесконечности 
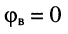
модуль волнового сопротивления 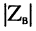
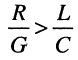
изменение фазы от нулевого значения при 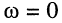

Коэффициент отражения
Что касается соотношения между комплексными амплитудами напряжения (тока) падающей и отражённой волн, то оно оказывается различным в различных сечениях линии. Установить эти соотношения можно из системы (23.8), положив 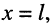
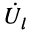
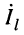
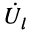
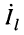
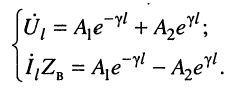
Из системы (24.11) согласно правилу Крамера получаем значения постоянных 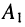
Подстановка найденных значений 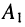
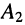
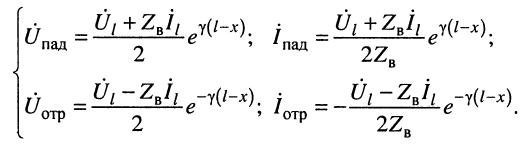
Система уравнений (24.12) позволяет записать отношение комплексных амплитуд напряжений и токов отражённой и падающей волн в сечении линии, расположенном на расстоянии 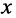
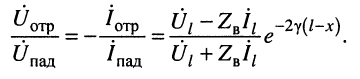
Но при выбранных направлениях отсчётов (рис. 24.2) напряжения 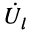
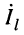
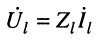
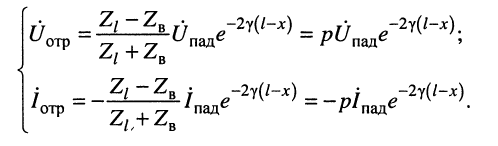
Определение:
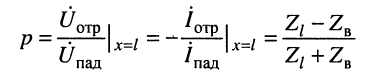
комплексной амплитуды напряжения отражённой волны к комплексной амплитуде напряжения падающей волны называется коэффициентом отражения.
Анализ соотношений (24.14) и (24.15) приводит к следующим выводам:
1. Коэффициент отражения является комплексной величиной и полностью зависит от волнового сопротивления линии 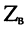
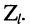
2. Коэффициент отражения по току отличается от коэффициента отражения по напряжению только знаком.
3. При 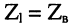
4. Отношение амплитуд отражённой и падающей волн (см. (24.14) и (24.15))
убывает с удалением от конца линии к её началу
5. В режиме короткого замыкания, когда 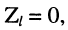
р = 1. Это означает, что напряжения отражённой и падающей волн в конце линии находятся в противофазе:
а результирующее напряжение равно нулю
при этом токи падающей и отражённой волн оказываются в фазе
и результирующий ток равен удвоенному току падающей волны
6. В режиме холостого хода, когда 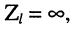
и результирующее напряжение равно удвоенному напряжению падающей волны
а ток равен нулю
Уравнения передачи согласованно нагруженной длинной линии
Ранее (см. разд. 23.3) были получены уравнения передачи длинной линии (23.8), которые представляют собой общее решение телеграфных уравнений и описывают закон распределения напряжений и токов по всей линии. Для решения же большинства практических задач достаточно знать соотношения лишь между напряжениями и токами на внешних зажимах линии и вовсе не интересоваться законом распределения напряжений и токов по длине линии. Иначе говоря, на практике вполне достаточно рассматривать линию как согласованно нагруженный четырёхполюсник, полностью описываемый соответствующими уравнениями передачи.
Поставим задачу найти уравнения передачи согласованно нагруженной линии, которые связывают комплексные амплитуды напряжений и токов на её внешних зажимах.
Воспользуемся уравнениями (24.12) для комплексных амплитуд напряжений и токов падающей и отражённой волн и подставим их в систему (24.9):
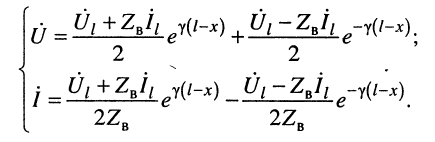
Если в систему (24.9) подставить выражения (24.14), получим
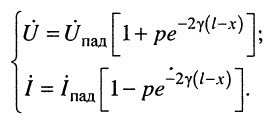
Системы (24.16) и (24.17) представляют собой системы уравнений передачи длинной линии. Обычно комплексные амплитуды напряжения и тока на входных зажимах линии (х = 0) обозначают через 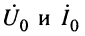
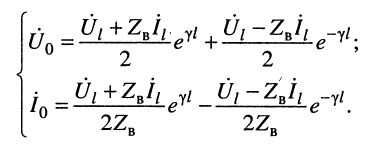
В большинстве случаев уравнения (24.8) записывают в более компактном виде:
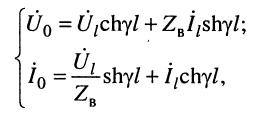
где
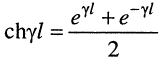
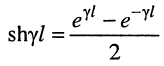
Для режима согласованной нагрузки, когда 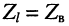
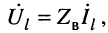
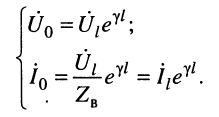
Именно в такой режим и стремятся поставить линию связи, поскольку отражённые волны вызывают ряд нежелательных явлений, о чём речь пойдёт далее.
Постоянная передачи и частотные характеристики длинной линии
Постоянная передачи длинной линии:
Определение
Безразмерная комплексная величина, равная произведению коэффициента распространения 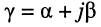
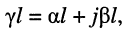
называется постоянной передачи линии.
Вещественная часть постоянной передачи 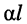
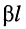
Постоянная передачи и входящие в неё параметры характеризуют линию как таковую и не зависят от свойств генератора и нагрузки, между которыми линия может быть включена.
Поскольку режим согласованной нагрузки для линии является типовым, найдём указанные ранее параметры только для этого режима.
В таком случае постоянную передачи можно получить, прологарифмировав уравнения (24.20):
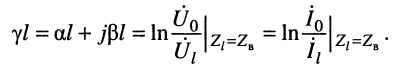
Подставляя отношения комплексных амплитуд
под знак логарифма, получаем:
на основании чего можно записать два равноправных выражения для коэффициента распространения
собственное затухание линии
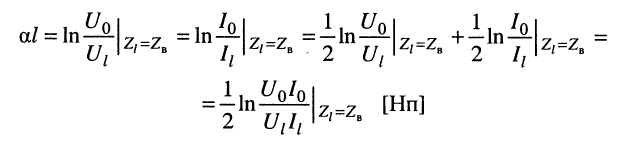
и её собственную фазу
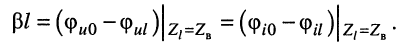
Из выражений (24.23) и (24.24) следует, что для согласованно нагруженной линии:
собственное затухание линии 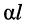
собственная фаза линии равна разности начальных фаз колебаний напряжений (токов) на входе и выходе.
Собственное затухание линии часто оценивается в децибелах:
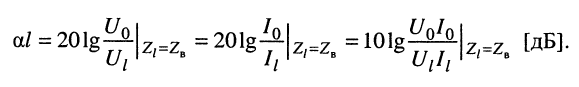
В этом случае нетрудно переформулировать зависимость собственного затухания, выраженного в децибелах, через десятичные логарифмы отношений амплитуд напряжений (токов) или полных мощностей.
Пример 24.1.
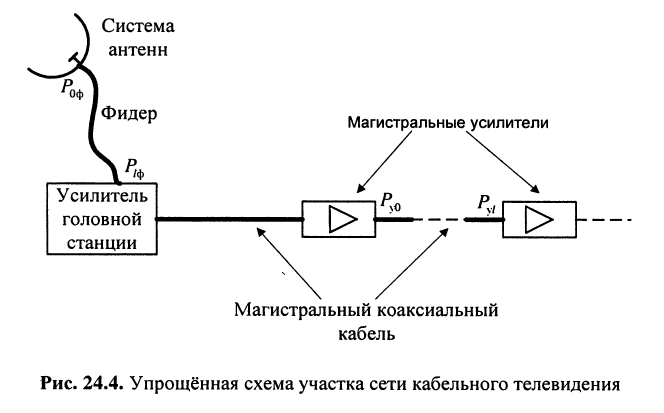
Оценим потери мощности телевизионного сигнала при распространении его в фидере’ от системы антенн до усилителя головной станции и в коаксиальном кабеле сети кабельного телевидения на отрезках магистральной линии между магистральными усилителями (рис. 24.4).
Решение. Затухание фидера зависит от его конструкции, длины 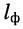
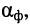
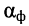
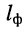
а отношение мощности сигнала на выходе фидера 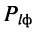
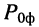
т. е. потери мощности в фидере невелики.
Фидер — линия для передачи электрических колебаний высокой частоты от радиопередатчика к антенне и от антенны к радиоприёмнику.
В то же время типовой магистральный коаксиальный кабель QR 540 JCA имеет полосу пропускания 5—1000 МГц и коэффициент затухания 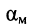
Расстояние 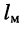
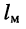
Последнее означает, что полная мощность на входе последующего усилителя 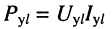
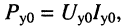
Частотные характеристики (АЧХ и ФЧХ) согласованно нагруженной длинной линии
Исходя из уравнений передачи согласованно нагруженной линии (24.20) запишем её комплексную частотную характеристику через постоянную передачи линии:
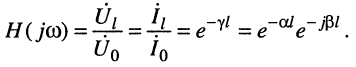
Отсюда нетрудно получить постоянную передачи через КЧХ линии:
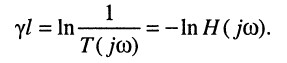
Амплитудно-частотная и фазочастотная характеристики определяются из (24.26):
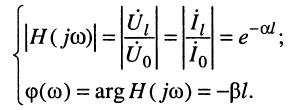
Для несогласованной нагруженной линии КЧХ можно найти из её уравнений передачи (24.18), подставив в них равенства:
где 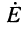
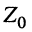
Входное сопротивление длинной линии
Определение:
Входным сопротивлением линии 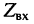
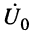
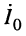
Формулу входного сопротивления для линии с произвольной нагрузкой можно получить из уравнений (24.17), если положить расстояние 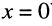
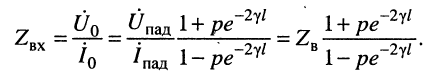
Анализ формулы (24.29) показывает:
при согласованной нагрузке входное сопротивление равно волновому, поскольку в данном случае 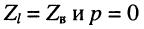
если постоянная передачи линии стремится к бесконечности 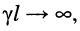
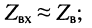
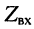
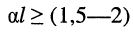
в режиме КЗ 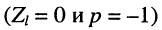
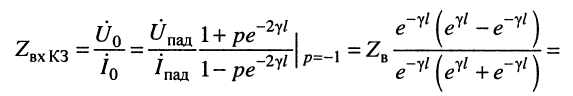
в режиме XX 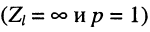
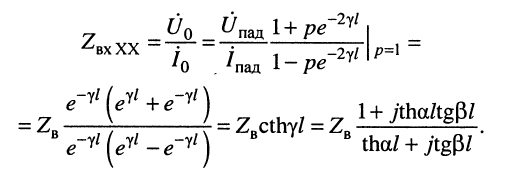
волновое сопротивление линии представляет собой предел, к которому стремится входное сопротивление при безграничном увеличении длины линии:
Этот факт объясняется тем, что при большом затухании линии значительная часть мощности, подводимой к её входу, рассеивается в самой линии и лишь небольшой остаток мощности поступает в нагрузку (см. пример 24.1). По этой причине энергетические соотношения на входе линии пренебрежимо мало зависят от энергетических соотношений на её выходе и, в частности, от сопротивления нагрузки линии.
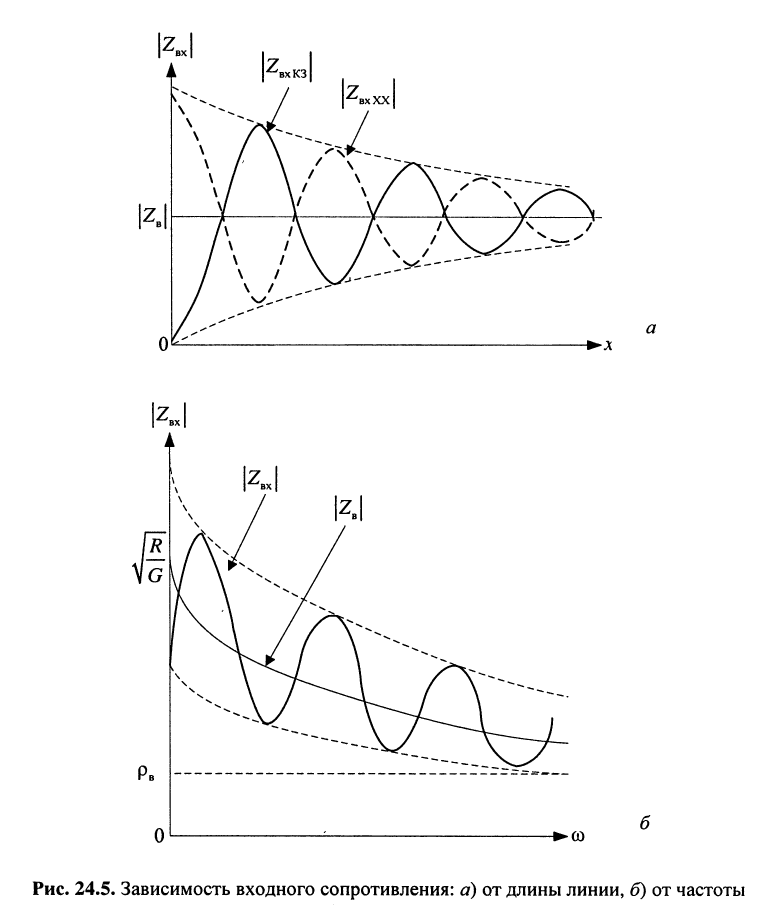
С увеличением длины линии увеличивается и её затухание, а потому уменьшается амплитуда отражённой волны на входе линии, что, в свою очередь, приводит к уменьшению отклонения входного сопротивления линии от её волнового сопротивления как по модулю, так и по фазе. В пределе входное сопротивление линии стремится к волновому сопротивлению. На рис. 24.5, а показаны зависимости модулей входных сопротивлений в режимах XX и КЗ. Колебательный характер волнового сопротивления при несогласованной нагрузке объясняется наличием падающих и отражённых волн.
Входное сопротивление зависит не только от длины линии, но и от частоты (рис. 24.5, б). С ростом частоты увеличиваются как собственное затухание 
Допустимые отклонения входного сопротивления линии от её волнового сопротивления строго нормированы, и при эксплуатации длинных линий необходимо придерживаться указываемых для линии обычно весьма жёстких норм.
Определение параметров линии методом холостого хода и короткого замыкания
Определение первичных и вторичных параметров линии наиболее просто осуществлять с помощью измерений входного сопротивления линии при двух граничных сопротивлениях нагрузки: холостом ходе и коротком замыкании.
Из уравнений (24.19) в режимах 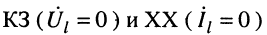
Совместное решение этих уравнений позволяет найти значения волновых параметров линии: волнового сопротивления и постоянной передачи.
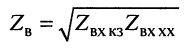
равно среднему геометрическому из входных сопротивлений короткозамкнутой и разомкнутой линии. Это выражение можно рассматривать как ещё одно определение волнового сопротивления длинной линии.
Гиперболический тангенс постоянной передачи
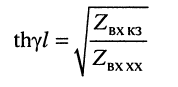
равен среднему геометрическому из сопротивления 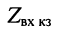
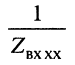
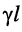
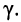
Логарифмируя обе части последнего равенства, получаем постоянную передачи:
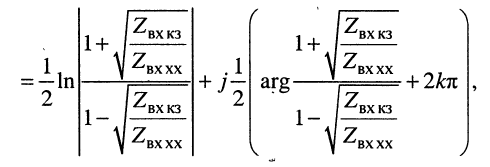
откуда легко находятся коэффициенты затухания и фазы:
Коэффициент 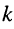
Во всех формулах необходимо брать только арифметические корни.
Зная волновые параметры линии, нетрудно вычислить её первичные параметры путём приравнивания вещественных и мнимых частей равенств:
Метод холостого хода и короткого замыкания целесообразно применять в том случае, когда затухание линии не превышает
1 Нп (8,69 дБ), что характерно для большинства длинных линий.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Колебания в линиях без потерь
- ЭДС и напряжение в электрической цепи
- Закон Ома для участка цепи
- Электрическое сопротивление
- Частотные методы анализа и расчёта электрических цепей
- Операторные передаточные функции
- Свободные колебания в пассивных электрических цепях
- Цепи с распределёнными параметрами
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎥 Видео
4.2 Решение волновых уравнений Гельмгольца в виде плоских бегущих волнСкачать

Билеты №32, 33 "Уравнения Максвелла"Скачать

Билеты №1 и №2 "Монохроматические волны"Скачать

Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Лекция №2 "Волновая оптика"Скачать

Установившийся синусоидальный режим. Метод комплексных амплитуд.Скачать

Урок 454. Понятие о волновой функцииСкачать

Якута А. А. - Механика - Волновое уравнение. Механические волны. Скорость распространения волнСкачать

Метод Фурье для волнового уравненияСкачать

Общая физика | Л23: Элементы теории волн. Волновое уравнение. Поперечные и продольные колебанияСкачать

*** Лекция. Волновое уравнение электромагнитной волны ******Скачать

5. Решение волнового уравнения на отрезке методом ФурьеСкачать

4.1. Общее решение волнового уравненияСкачать

Урок 370. Механические волны. Математическое описание бегущей волныСкачать

Амплитуда, период, частота и длина волны периодических волнСкачать

4.1 Однородные волновые уравнения ГельмгольцаСкачать





 – фазовая скорость (скорость перемещения фазового фронта). Если b(w), то vф(w), причем может быть vф > c. Означает ли это, что можно передать информацию со скоростью, превышающей скорость света с ?
– фазовая скорость (скорость перемещения фазового фронта). Если b(w), то vф(w), причем может быть vф > c. Означает ли это, что можно передать информацию со скоростью, превышающей скорость света с ? . Каждой составляющей спектра соответствует плоская гармоническая волна, следовательно в точке z > 0 имеем:
. Каждой составляющей спектра соответствует плоская гармоническая волна, следовательно в точке z > 0 имеем:  . Если b=b(w), можем перейти к пространственному спектру, т. е. dw®db, тогда
. Если b=b(w), можем перейти к пространственному спектру, т. е. dw®db, тогда  . Выделим вблизи максимума огибающей спектра с частотой wо участок спектра 2Dw = w1 — w2. Пусть Dw vф (vф
. Выделим вблизи максимума огибающей спектра с частотой wо участок спектра 2Dw = w1 — w2. Пусть Dw vф (vф совпадают по направлению – дисперсия положительная, Если
совпадают по направлению – дисперсия положительная, Если  ). Чтобы гармоническая волна сохраняла форму при любой частоте, необходимо, чтобы в числе решений было решение вида: p = eiw t ± i (kr). Пусть Â переводит р в некоторую функцию q: Â( p) = q. Если qº0, то p – свободная волна в данной среде. Продифференцируем по t, учитывая линейность и однородность Â:
). Чтобы гармоническая волна сохраняла форму при любой частоте, необходимо, чтобы в числе решений было решение вида: p = eiw t ± i (kr). Пусть Â переводит р в некоторую функцию q: Â( p) = q. Если qº0, то p – свободная волна в данной среде. Продифференцируем по t, учитывая линейность и однородность Â:  , т. е.
, т. е.  , где комплексная амплитуда
, где комплексная амплитуда  не зависит от t, но может зависеть от w. Подставив p и q в уравнение Â( p) = q, получим уравнение, не зависящее от t, и содержащее w как параметр. Если продифференцировать по координатам, получим: Ñq=ÑÂ(p)=Â(±ikp)= ±ikÂ(p)= ±ikq, т. е. Ñq=±ikq, следовательно, можно представить q в виде: q=f(w,k)eiw t ± i(kr), где f(w,k) кроме w и k может зависеть только от коэффициентов оператора. При произвольных w и k p = eiw t ± i (kr) не свободная волна, т. к. не является решением уравнения Â( p) = 0. Чтобы определить, какие свободные волны могут распространяться (имеют право на существование) в данной среде, необходимо выбрать такие w и k, чтобы
не зависит от t, но может зависеть от w. Подставив p и q в уравнение Â( p) = q, получим уравнение, не зависящее от t, и содержащее w как параметр. Если продифференцировать по координатам, получим: Ñq=ÑÂ(p)=Â(±ikp)= ±ikÂ(p)= ±ikq, т. е. Ñq=±ikq, следовательно, можно представить q в виде: q=f(w,k)eiw t ± i(kr), где f(w,k) кроме w и k может зависеть только от коэффициентов оператора. При произвольных w и k p = eiw t ± i (kr) не свободная волна, т. к. не является решением уравнения Â( p) = 0. Чтобы определить, какие свободные волны могут распространяться (имеют право на существование) в данной среде, необходимо выбрать такие w и k, чтобы  . Это уравнение называют дисперсионным уравнением. Каждому значению w соответствует решение этого уравнения относительно k, и каждому k – относительно w. Для изотропной среды это уравнение содержит только |k| и его можно привести к виду
. Это уравнение называют дисперсионным уравнением. Каждому значению w соответствует решение этого уравнения относительно k, и каждому k – относительно w. Для изотропной среды это уравнение содержит только |k| и его можно привести к виду  – дисперсионное уравнение для данной среды.
– дисперсионное уравнение для данной среды. . Ищем волну в виде: j = еiw t – i k x – k z. Получаем дисперсионное уравнение:
. Ищем волну в виде: j = еiw t – i k x – k z. Получаем дисперсионное уравнение:  . Отсюда vф= g /w, т. е. vф зависит от w, следовательно, существует нормальная дисперсия (vф
. Отсюда vф= g /w, т. е. vф зависит от w, следовательно, существует нормальная дисперсия (vф , где G – коэффициент изгибной жесткости. Ищем решение в виде: еiw t – i k x, получаем дисперсионное уравнение
, где G – коэффициент изгибной жесткости. Ищем решение в виде: еiw t – i k x, получаем дисперсионное уравнение  , откуда
, откуда  , т. е. имеется аномальная дисперсия (vф
, т. е. имеется аномальная дисперсия (vф q – угол падения, q¢– угол отражения,
q – угол падения, q¢– угол отражения, exp[-ik1(-ycosq+zsinq)],
exp[-ik1(-ycosq+zsinq)], exp[-k1(ycosq¢+zsinq¢)].
exp[-k1(ycosq¢+zsinq¢)]. exp[-ik2(ycosy+zsiny)].
exp[-ik2(ycosy+zsiny)]. откуда
откуда  ,
,  ,
, ,
,  ,
,
















 . Используя условие стационарности
. Используя условие стационарности  , получаем:
, получаем:  . Учитывая, что
. Учитывая, что  ,
,  , где q – угол между направлением луча и нормалью к границе раздела, имеем: n1sinq1 = n2sinq2 – закон преломления.
, где q – угол между направлением луча и нормалью к границе раздела, имеем: n1sinq1 = n2sinq2 – закон преломления.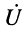
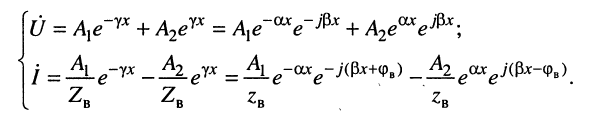
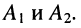
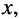 т. е. в любом сечении линии, и напряжение
т. е. в любом сечении линии, и напряжение 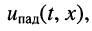 и ток
и ток 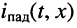 являются гармоническими колебаниями;
являются гармоническими колебаниями;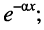
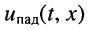 к амплитуде тока
к амплитуде тока 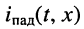 равно модулю волнового сопротивления
равно модулю волнового сопротивления 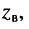 а разность фаз между ними равна аргументу
а разность фаз между ними равна аргументу 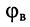 волнового сопротивления линии;
волнового сопротивления линии;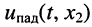 или тока
или тока 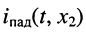 в сечении
в сечении 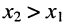 отстаёт по фазе от колебания и
отстаёт по фазе от колебания и 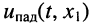 или
или 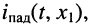 поскольку коэффициент фазы является величиной положительной:
поскольку коэффициент фазы является величиной положительной: 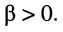
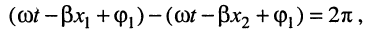
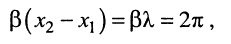
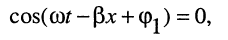
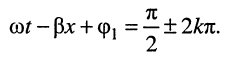
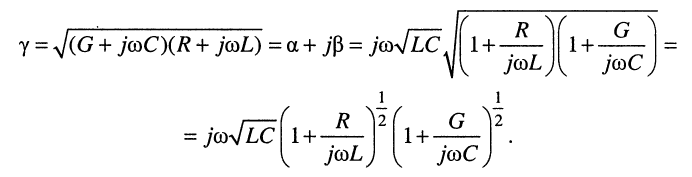
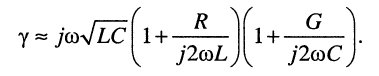
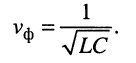
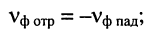
 (ток) в любой точке длинной линии
(ток) в любой точке длинной линии  х является суммой напряжений (токов) падающей и отражённой волн:
х является суммой напряжений (токов) падающей и отражённой волн: