Волновое число как найти из уравнения (7 видео)

Волновое число: физический смысл, размерность, формулы, примеры расчета

Вы хотите знать, в чем разница между волновым числом и угловым волновым числом и как их рассчитать? Тогда эта статья как раз для вас. Мы подробно объясним эту тему и покажем на примере, как можно рассчитать эти величины.

Если вы рассматриваете электромагнитную волну с определенной длиной волны, то волновое число является обратным этой длине волны — оно ведет себя противоположным образом. Например, если длина волны увеличивается, волновое число уменьшается. Если, с другой стороны, длина волны уменьшается, то волновое число увеличивается.

Содержание

Волновое число в спектроскопии
Единица измерения волнового числа
Разница между волновым числом и угловым волновым числом
Пример расчета волнового числа
Пример расчета углового волнового числа
Преобразование длины волны в волновой число
Волновое число как найти из уравнения
Волновое уравнение Wave equation
Волновое число как найти из уравнения
📸 Видео

Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Волновое число в спектроскопии

Волновое число k определяется в спектроскопии как обратная величина длины волны λ, то есть ξ = 1 / λ (называется еще пространственной частотой). Однако его также можно выразить через частоту f и скорость света в вакууме c, тогда ξ = f / c или также через число n длин волн, укладывающихся в определенную длину l, то есть ξ = n / l .

В целом, для волнового числа применимо следующее соотношение: ξ = 1 / λ = f / c = n / l .

Важно: Волновое число ξ не следует путать с частотой f. Частота имеет единицу измерения Гц = 1 / с = с -1 и определяется через обратную величину периода T: f = 1 / T . Она показывает, как часто электромагнитная волна колеблется в секунду.

Видео:Билет №36 "Волновод"Скачать

Единица измерения волнового числа

Обычно волновое число выражается в в следующих единицах измерения (в СИ): 1 / м = м -1 , что соответствует числу колебаний на метр. Однако единица может быть также преобразована, например, в единицы 1 / см = см -1 или 1 / мм = мм -1 .

Между этими единицами измерения существует следующая взаимосвязь: 1 м -1 = 0,01 см -1 = 0,001 мм -1 , соответственно 1 мм -1 = 100 см -1 = 1000 м -1 .

Видео:Билет №34 "Электромагнитные волны"Скачать

Разница между волновым числом и угловым волновым числом

Угловое волновое число часто ошибочно называют просто волновым числом. Однако, угловое волновое число k является величиной волнового вектора k и связано с волновым числом ξ следующим образом: k = | k | = 2*π*ξ = ω / c = 2*π / λ . В этой формуле где ω представляет собой так называемую угловую частоту. Волновой вектор — это вектор, перпендикулярный волновому фронту волны. Эта формула показывает, что волновое число ξ также может быть вычислено из углового волнового числа k: ξ = k / 2*π .

Важно: Угловую частоту и частоту также нельзя путать друг с другом. Угловая частота ω связана с частотой f следующим образом: ω = 2*π*f .

Физический смысл волнового числа.

Волновое число численно равно числу периодов волны, укладывающихся в отрезок 2π метров. Это пространственный аналог круговой частоты ω (рад·с -1 ). Характеристика периодического процесса в пространстве.

Видео:Получение уравнения плоской бегущей волны.Скачать

Пример расчета волнового числа

Если мы наблюдаем электромагнитную волну с длиной волны λ = 500 нм и хотим вычислить по ней волновое число ξ, то поступаем следующим образом. Чтобы получить размерность м -1 сначала переведите длину волны в метры. То есть 500 нм = 500 * 10 -9 м = 5*10 -7 м.

Используя представленную выше формулу, вы можете определить соответствующее волновое число: ξ = 1 / λ = 1 / 5*10 -7 = 2*10 6 м -1 .

На одном метре волна колеблется 2 миллиона раз. Если преобразовать единицу измерения, то можно сказать, что волна колеблется 2000 раз на одном миллиметре: 2 * 10 6 м -1 = 0,001 * 2 * 10 6 мм -1 = 2000 мм -1 .

Видео:Урок 455. Уравнение ШрёдингераСкачать

Пример расчета углового волнового числа

Если использовать ту же длину волны λ = 500 нм =5 *10 -7 м, как в предыдущем примере, и подставьте это значение в формулу для расчета углового волнового числа, то это приведет к следующим результатам: k = 2 * π / λ = 2 * π / 5 *10 -7 м = 1,2566 * 10 7 м -1 .

Легко видеть, что угловое волновое число k отличается от волнового числа ξ из предыдущего примера:

ξ = 2*10 6 м -1 ↔ k = 1,2566 * 10 7 м -1

Видео:Лекция 2 ВолныСкачать

Преобразование длины волны в волновой число

В следующей таблице показаны два направления преобразования из длины волны в волновое число и наоборот. Кроме того, в последней колонке перечислены некоторые области применения спектроскопии:

Видео:Волновое движение. Механические волны. 9 класс.Скачать

Волновое число как найти из уравнения

Волновое уравнение
_{Wave equation}

Волновое уравнение − линейное дифференциальное уравнение в частных производных, описывающее малые колебания струны, колебательные процессы в сплошных средах и в электродинамике.
В общем случае волна, распространяющаяся в пространстве, описывается уравнением

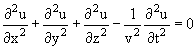(1)

где u = u(x,y,z,t) − возмущение в точке x,y,z в момент времени t, v − скорость распространения волны. Уравнение (1) инвариантно относительно замены Монохроматическая волна − распространение колебаний с определённой частотой ω. В случае одномерного распространения волны вдоль оси x формула монохроматической волны имеет вид

u(x,t) = Asin(ωt − xv).

Длина волны λ − путь, пройденный возмущением (состоянием с определённой фазой) за время равное периоду колебаний T

Частота ω и период колебаний T связаны соотношением

Эквивалентные формулы для монохроматической волны, распространяющейся вдоль оси x

u(x,t) = Asin(ωt − kx) = Asinω(t − x/v) = Asin2π(t/T − x/λ).

u(r,t) = (A/r)sin(ωt − kr).

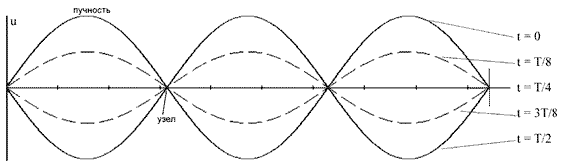
Стоячая волна. При наложении монохроматических волн одинаковой частоты образуется устойчивая картина результирующих колебаний с характерными максимумами и минимумами.

Стоячая волна образуется в системах с двумя жёстко закреплёнными точками. При отражении фаза волны меняется на π и происходит интерференция падающей и отраженной волн.

Падающая волна	u₁ = Asin(ωt + kx)
Отражённая волна	u₂ = Asin(ωt − kx + π)
Стоячая волна	u₁ + u₂ = A(x)cosωt	(2)

Соотношение (2) можно получить, используя формулу

sinα − sinβ = 2sin[(α − β)/2] cos[(α + β)/2]

и положив 2Asin(2πx/λ) = A(x), A(x) − амплитуда стоячей волны.

Видео:Волны. Основные понятия. Решение задач.Задача 1Скачать

Волновое число как найти из уравнения

Уравнения плоской и сферической волн

Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t.

(5.2.1)

Эта функция должна быть периодической как относительно времени, так и координат (волна – это распространяющееся колебание, следовательно периодически повторяющееся движение). Кроме того, точки, отстоящие друг от друга на расстоянии l, колеблются одинаковым образом.

Уравнение плоской волны

Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер.

Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t: . Пусть колебание точек, лежащих в плоскости , имеет вид (при начальной фазе )

(5.2.2)

Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время .

Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости , т.е.

(5.2.3)

– это уравнение плоской волны.

Таким образом, x есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания . Это будет, если энергия волны не поглощается средой.

Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z.

В общем виде уравнение плоской волны записывается так:

, или

(5.2.4)

Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны.

Уравнение (5.2.3) описывает волну, распространяющуюся в сторону увеличения x. Волна, распространяющаяся в противоположном направлении, имеет вид:

Уравнение волны можно записать и в другом виде.

Введем волновое число , или в векторной форме:

(5.2.5)

где – волновой вектор, – нормаль к волновой поверхности.

Так как , то . Отсюда . Тогда уравнение плоской волны запишется так:

(5.2.6)

Уравнение сферической волны

В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической.

Предположим, что фаза колебаний источника равна wt (т.е. ). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону . Следовательно, уравнение сферической волны:

, или

(5.2.7)

где А равна амплитуде на расстоянии от источника равном единице.

Уравнение (5.2.7) неприменимо для малых r, т.к. при , амплитуда стремится к бесконечности. То, что амплитуда колебаний , следует из рассмотрения энергии, переносимой волной.