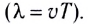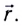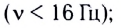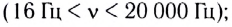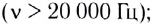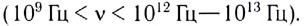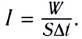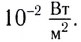Бегущие волны – это волны, которые переносят энергию в пространстве. Количественно транспортирование энергии этой волной назначает вектор плотности потока энергии, называемый вектором Умова-Пойтинга. Его направление совпадает с направлением распространения энергии. Модуль вектора равняется энергии, которую может переносить волна за время, равное 1 с , через площадку, располагаемую перпендикулярно к направлению ее движения с площадью, равняющуюся 1 .
- Уравнение плоской бегущей волны
- Что называют электромагнитной волной. Волновое число
- Уравнение сферической бегущей волны
- Волновое движение в физике — формулы и определение с примерами
- Уравнение бегущей волны
- Физический смысл волнового числа
- Фронт волны и волновая поверхность
- Стоячие волны
- Интерференция волн
- Условие максимума и минимума при интерференции двух волн
- Распространение волн. Принцип Гюйгенса – Френеля
- Дифракция механических волн
- Условие возникновения стоячей волны в струне
- Визуализация звуковых волн
- Распространение колебаний в упругих средах. Продольные и поперечные волны
- Звуковые волны. Скорость звука. Ультразвук
- Презентация по физике «Волны. Уравнение бегущей волны»
- Описание презентации по отдельным слайдам:
- Дистанционное обучение как современный формат преподавания
- Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Физика: теория и методика преподавания в образовательной организации
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 💡 Видео
Видео:Физика. 11 класс. Упругие механические волны. Уравнение бегущей и стоячей волны /16.11.2020/Скачать

Уравнение плоской бегущей волны
Для получения уравнения бегущей волны рассматривается плоская гармоническая. Считается, что она распространяется по О х . Поверхности волны перпендикулярны О х , все точки волновой поверхности совершают колебания одинаково, смещение ξ = ξ ( x , t ) будет функцией с координатой x и временем t . Запись уравнение колебаний частиц, находящихся на плоскости х , примет вид:
ξ ( x , t ) = A cos ω t — x υ ( 1 ) .
Отсюда ξ ( x , t ) является периодической по времени и по координате х . уравнение ( 1 ) называют уравнением бегущей волны. Если плоская волна задается при помощи выражения ( 1 ) , то ее перемещение идет по О х . При обратном ее направлении по О х уравнение запишется как:
ξ ( x , t ) = A cos ω t + x υ ( 2 ) .
Если волна движется по О х без поглощения энергии, то это характеризуется уравнением:
ξ ( x , t ) = A cos ω t — x υ + φ 0 ( 3 ) .
Значение A = c o n s t относят к амплитуде, ω – к циклической частоте волны, φ 0 — к начальной фазе колебаний, определяемой выбором началом отсчета x и t , ω t — x υ + φ 0 – к фазе плоской волны.
Видео:Урок 370. Механические волны. Математическое описание бегущей волныСкачать

Что называют электромагнитной волной. Волновое число
Электромагнитные волны – это распространяющиеся в пространстве изменения состояния электромагнитного поля. Они характеризуются волновым числом k .
Запись выражения ( 1 ) примет совершенно другой вид при известном волновом числе.
Если перейти к комплексным числам, применив формулу Эйлера, уравнение плоской волны зафиксируем.
Выражение ( 6 ) имеет физический смысл только в действительной части, но R e возможно опустить в записи уравнения волны.
Перейдем к рассмотрению волнового процесса, где не происходит изменение фазы.
Далее найдем дифференциал от выражения ( 7 ) .
При условии, что υ волны зависит от частоты колебаний, то такая волна подвержена дисперсии.
Видео:Физика 11 класс (Урок№2 - Механические волны.)Скачать

Уравнение сферической бегущей волны
Сферическая волна – это волна, волновая поверхность которой является концентрической сферой. Такое уравнение примет вид:
ξ ( r , t ) = A 0 r cos ω t — k r + φ 0 ( 11 ) ,
где r является расстоянием от центра волны до точки рассмотрения. Если имеем дело со сферической волной, то ее амплитуда колебаний не будет постоянной даже при условии, что энергия не поглощается средой. Ее убывание происходит обратно пропорционально расстоянию. Выполнение уравнения ( 8 ) возможно тогда, когда источник волн считается точечным.
Уравнение бегущей волны в любом виде подчинено волновому уравнению.
Дана плоская электромагнитная волна в вакууме, которая распространяется по О х . Амплитуда напряженности электрического поля равняется E m . Определить амплитуду напряженности магнитного поля заданной волны.
За основу необходимо принять выражение для амплитуд электромагнитной волны:
ε ε 0 E = μ μ 0 H ( 1 . 1 ) .
Запись уравнения колебаний модуля E → в электромагнитной волне при условии, что она является плоской и идет по О х , фиксируем:
E = E m cos ω t — k x ( 1 . 2 ) .
Для записи уравнения колебаний H → в электромагнитной волне, в случае если она считается плоской и распространяется по О х :
H = H m cos ω t — k x ( 1 . 3 ) .
Из условия имеем, что волна производит рассеивание в вакууме, то ε = 1 , μ = 1 . Применяя ( 1 . 1 ) , ( 1 . 2 ) , ( 1 . 3 ) :
ε 0 E m = μ 0 H m → H m = ε 0 μ 0 E m .
Ответ: H m = ε 0 μ 0 E m .
Распространение электромагнитной плоской волны идет в вакууме по О х . Ее падение производится перпендикулярно поверхности тела, которое способно полностью поглощать волну. Значение амплитуды напряженности магнитного поля равняется
H m . Определить давление волны на тело.
Необходимо учитывать, что тело, которое поглощает падающую на него энергию, оказывается под давлением, равным среднему значению объемной плотности энергии в электромагнитной волне.
Следует применять соотношение амплитуд электромагнитной волны, которое записывается:
ε ε 0 E = μ μ 0 H .
Для того, чтобы зафиксировать уравнение колебаний E при распространении волны по О х , получим:
E = E m cos ω t — k x .
Теперь перейдем к уравнению колебаний H , если рассеивание плоской волны идет соответственно направлению О х . Запишем:
H = H m cos ω t — k x .
Следует, что значение объемной плотности электрической энергии примет вид:
ω E = ε ε 0 E 2 2 .
Формула плотности магнитного поля:
ω H = μ μ 0 H 2 2 .
Причем ω E = ω H . Запись примет вид:
ω = ω E + ω H = 2 ω H = μ μ 0 H 2 = μ μ 0 H m 2 cos 2 ω t — k x .
После усреднения плотности, имеем:
» open=» ω = » open=» μ μ 0 H m 2 cos 2 ω t — k x .
При » open=» cos 2 ω t — k x = 1 2 получаем:
p = » open=» ω = μ μ 0 H m 2 2 .
Ответ: p = » open=» ω = μ μ 0 H m 2 2 .
Видео:Что такое волна (или волна в физике)Скачать

Волновое движение в физике — формулы и определение с примерами
Содержание:
Волновое движение:
Процесс распространения колебаний в упругой среде называют механической волной. Для механических волн нужна среда, обладающая способностью запасать кинетическую и потенциальную энергию, она должна обладать инертными и упругими свойствами.
Различают поперечные и продольные волны. Продольные волны могут распространяться в любых средах: твердых, жидких и газообразных; поперечные – только в твердых средах.
Как в поперечных, так и в продольных волнах переноса вещества в направлении распространения волны не происходит. Волны переносят энергию колебаний.
Изучив страницу, вы сможете:
- исследовать образование стоячих звуковых волн в воздухе;
- объяснять механизм образования стоячих волн, определять узлы и пучности, используя графический метод;
- исследовать интерференцию от двух источников на поверхности воды;
- объяснять принцип Гюйгенса и условия наблюдения дифракционной картины механических волн.
Видео:Упругие механические волны. 1 часть. 11 класс.Скачать

Уравнение бегущей волны
Колебательное движение тела в упругой среде является источником механической волны.
Волну, переносящую энергию, называют бегущей волной.
В однородной среде скорость распространения волны остается величиной постоянной. Смещение y (x, t) от положения равновесия частиц среды при распространении волны зависит от координаты x на оси 0х, вдоль которой распространяется волна, и от времени t по закону:
где
Введем волновое число 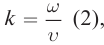
Смещение точек упругой среды в волне, бегущей в противоположном направлении выбранной оси 0х, можно определить по формуле:
Вспомните! Основные характеристики волн. Волны, созданные источником, совершающим гармонические колебания, характеризуются амплитудой колебания частиц среды A, частотой 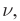
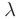
Длиной волны 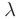
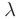
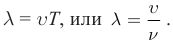
Видео:Механические модели волн. 1.Скачать

Физический смысл волнового числа
Запишем формулу (2), выразив циклическую частоту через период 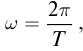
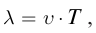
Бегущая волна обладает двойной периодичностью – во времени и в пространстве. Временной период равен периоду колебаний T частиц среды, пространственный период равен длине волны 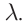
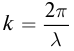
Видео:5.6 Механические волны. Виды волнСкачать
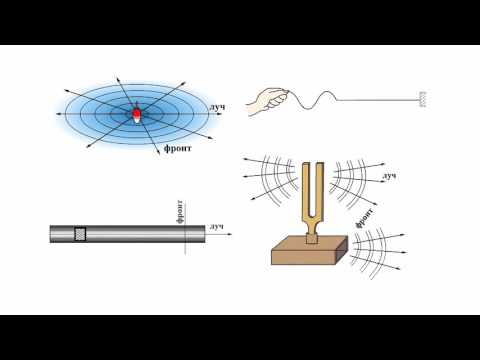
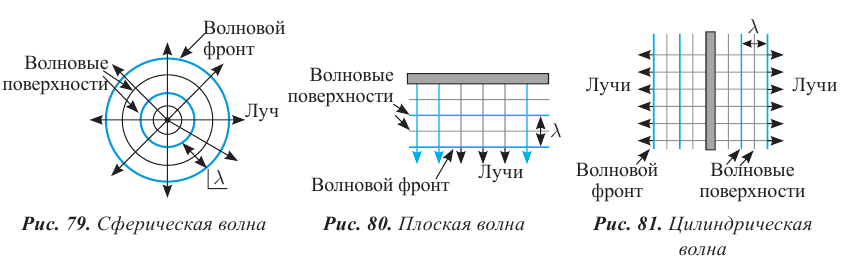
Фронт волны и волновая поверхность
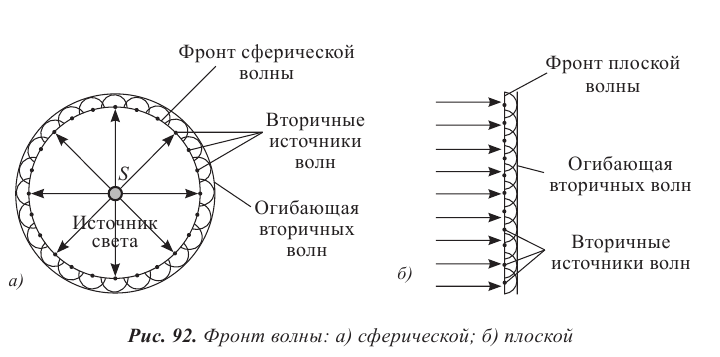
Волна за время, равное периоду колебаний, достигает точек пространства, расположенных от источника на расстоянии длины волны. Совокупность этих точек представляет собой фронт волны, который отделяет колеблющиеся точки среды от точек, не вовлеченных в колебательное движение. Фронт волны от точечного источника представляет собой сферу, от плоской пластины – плоскость, от струны – форму цилиндра (рис. 79–81).
Фронт волны – это геометрическое место точек пространства, до которых дошли колебания в данный момент времени t.
Направление распространения волны указывает луч, который перпендикулярен фронту волны.
В волне можно рассмотреть множество поверхностей, все точки которых совершают колебания синфазно, их называют волновыми поверхностями. При множестве волновых поверхностей, фронт волны только один.
Геометрическое место точек пространства, которые совершают колебания в одинаковой фазе в данный момент времени, называют волновой поверхностью.
Видео:Волновое движение. Механические волны. 9 класс.Скачать

Стоячие волны
Уравнение стоячей волны При отражении от более плотной среды волна, изменив свое направление на обратное, меняет фазу на 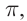
Получим уравнение стоячей волны путем сложения уравнений бегущих волн:
Заменив волновое число его значением 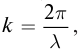
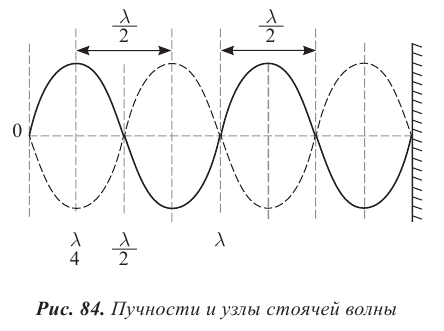
Координаты точек пучностей и узлов определяются из условий наибольшего и наименьшего значений амплитуды. При 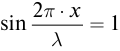
При 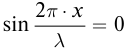
Расстояния между двумя соседними пучностями или двумя соседними узлами равны:
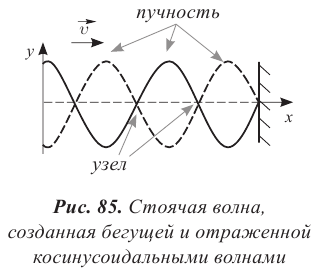
В стоячей волне нет потока энергии. Колебательная энергия, заключенная в отрезке струны между двумя соседними узлами, не переносится в другие части струны. В каждом таком отрезке происходит дважды за период превращение кинетической энергии в потенциальную и обратно как в обычной колебательной системе. Отсутствие переноса энергии является отличительной особенностью стоячей волны.
Пример:
Уравнение бегущей волны, изображенной на рисунке (рис. 85): 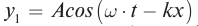
А. Получите уравнение стоячей волны как сумму падающей и отраженной волн.
В. Полученное выражение запишите, заменив волновое число и циклическую частоту через длину волны и период.
С. Определите положение узлов и пучностей.
Дано:
Решение: А. Уравнение стоячей волны определятся сложением уравнений бегущих волн:
В.
С. При 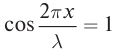
С. Расстояние от узлов определим из условия 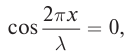
Ответ:
Интерференция волн
Если в некоторой среде несколько источников возбуждают механические волны, то они распространяются независимо друг от друга. Все точки среды принимают участие в колебаниях, вызванных каждой волной в отдельности. Наложение волн, в результате которой появляется устойчивая картина чередующихся максимумов и минимумов колебаний частиц среды, называют интерференцией.
Интерферировать могут только волны, имеющие одинаковую частоту и постоянный сдвиг фаз. Такие волны называют когерентными, их создают источники, колеблющиеся с одинаковой частотой и постоянным значением сдвига фаз.
Интерференция волн – взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга.
Интерференция бывает стационарной и нестационарной. Стационарную интерференционную картину могут давать только когерентные волны: например, две сферические волны на поверхности воды, распространяющиеся от двух когерентных точечных источников (рис. 87).
Запомните! Волны называют когерентными, если их источники совершают колебания одной частоты с постоянным сдвигом фаз.
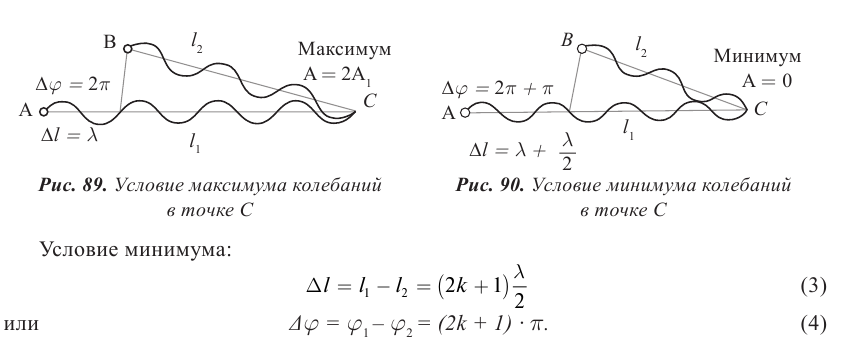
Условие максимума и минимума при интерференции двух волн
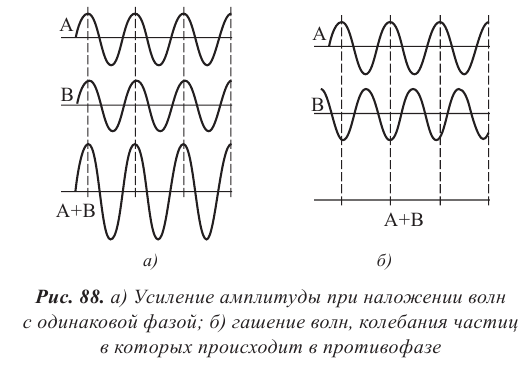
Амплитуда колебаний при наложении волн определяется в соответствии с принципом суперпозиции (рис. 88). Если в некоторой точке среды накладываются гребни когерентных волн, то происходит усиление колебаний, амплитуда принимает значение, равное сумме амплитуд. Если накладывается гребень одной волны с впадиной другой волны, то при равенстве амплитуд отдельно взятых волн данная точка пространства не совершает колебания. Если амплитуды отличаются, то колебания в этой точке совершаются с амплитудой равной разности амплитуд распространяющихся волн.
Для определения результата интерференции волн, распространяющихся от двух источников А и В, находящихся на расстоянии 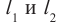
где 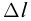
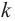
так как волна за период пробегает расстояние равное длине волны 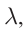
Минимум колебаний в рассматриваемой точке среды наблюдается в том случае, если от двух когерентных источников распространяются волны со сдвигом фаз, равным нечетному числу p, а разность хода лучей кратна нечетному числу полуволн. В этом случае колебания происходят в противофазе (рис. 90).
Возьмите на заметку:
Интерференция волн приводит к перераспределению энергии колебаний между частицами среды. Это не противоречит закону сохранения энергии, так как в среднем, для большой области пространства, энергия результирующей волны равна сумме энергий интерферирующих волн.
Распространение волн. Принцип Гюйгенса – Френеля
На основе принципа Х. Гюйгенса: каждая точка среды, до которой дошло возмущение, является источником вторичных волн, невозможно объяснить, почему источники вторичных волн создают фронт только по направлению распространения волны. Для объяснения явлений распространения волны французский физик О. Френель в 1815 г. дополнил принцип Х. Гюйгенса представлениями о когерентности и интерференции вторичных волн. При наложении вторичных когерентных волн происходит интерференция, в результате которой амплитуда колебаний в различных точках пространства становится разной: по направлению распространения волны усиливается, в обратном направлении – уменьшается. Огибающая фронты вторичных волн является фронтом результирующей волны (рис. 92).
Дифракция механических волн
Вторичные волны, созданные точками среды, которые находятся на краю отверстия или препятствия, искривляются и волна огибает препятствие (рис. 93 а–г).
Дифракция – это явление огибания волнами препятствий.
Все волны способны огибать препятствия, если длина волны соизмерима с размерами препятствия. Дифракция становится заметной, если размеры препятствия меньше длины волны.
Физика в нашей жизни:
Струнные музыкальные инструменты
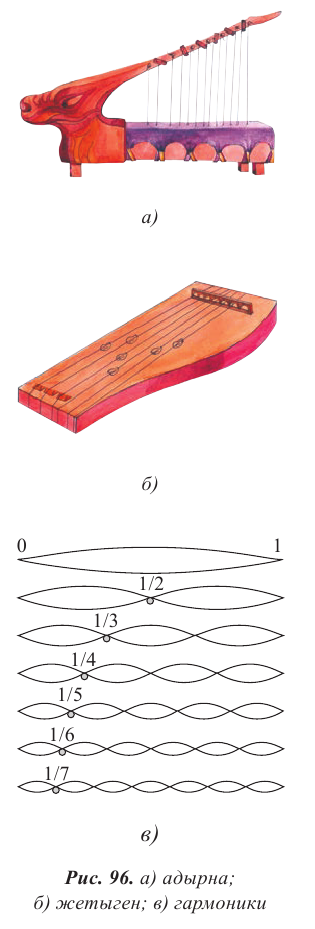
Интересно знать! Адырна (рис. 96 а) – один из древнейших казахских струнных инструментов. В его форме отобразилась воинственность кочевников-казахов: он напоминает изогнутый лук воина. Деревянный корпус инструмента легкий, так как он пустотелый. Струны изготавливают из кусков специально выделанной кожи или сплетенных из верблюжьей шерсти нитей. Музыкант играет, перебирая струны. Их в инструменте 13. Жетыген (рис. 96 б) – семиструнный музыкальный инструмент. Он имеет прямоугольную форму, изготовлен из дерева, струны – из конского волоса. Легенда о жетыгене раскрывает причину использования именно семи струн. Старик, потерявший семерых сыновей, вылил свое горе, исполняя кюи о них. Вспоминая каждого из сыновей, он натягивал новую струну на музыкальном инструменте.
Условие возникновения стоячей волны в струне
Стоячая волна в струне возникает только в том случае, если длина 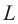
Набору значений 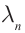
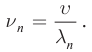
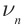
В отличие от груза на пружине или маятника, у которых имеется единственная собственная частота, струна обладает бесконечным числом собственных резонансных частот. На рисунке 96 в изображены несколько типов стоячих волн в струне. Стоячие волны различных типов могут одновременно присутствовать в колебаниях струны.
Визуализация звуковых волн
Существует несколько способов демонстрации стоячей волны, один из них – фигуры Хладни (рис. 97). Немецкий физик Эрнст Хладни получал узор, посыпая пластинку песком и проводя по краю смычком. Движения смычка заставляли пластинку колебаться на некоторой резонансной частоте. Песок скапливался и лежал неподвижно в узлах, а на участках, где отраженная волна усиливала бегущую, песок смещался.
Интересно знать! В Шотландии есть рослинская капелла св. Матвея, на одной из арок которой есть 213 резных каменных кубов, с вырезанным на них геометрическим рисунком. Многие исследователи пытались понять, что зашифровано в рисунках на кубах. Отставной генерал ВВС Томас Митчел со своим сыном, пианистом Стюартом Митчелом предложили оригинальный способ расшифровки послания. Они сопоставили геометрические рисунки с фигурами Хладни и пришли к выводу, что на кубах записаны ноты. Собрав ноты воедино и творчески обработав их, они представили миру произведение «Рослинский Мотет».
Итоги:
Глоссарий
Волновая поверхность – геометрическое место точек, имеющих одинаковую фазу колебаний.
Дифракция – явление огибания волнами препятствий.
Интерференция волн – взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга.
Когерентные волны – волны, имеющие одинаковую частоту и постоянный сдвиг фаз.
Механическая волна – процесс распространения колебаний в упругой среде.
Фронт волны – геометрическое место точек пространства, до которых дошли колебания в данный момент времени t.
Видео:Получение уравнения плоской бегущей волны.Скачать

Распространение колебаний в упругих средах. Продольные и поперечные волны
Опыт показывает, что колебания, возбужденные в какой-либо точке упругой среды, с течением времени передаются в ее другие точки. В качестве примера достаточно вспомнить, что измерение пульса осуществляется на запястье, хотя сердце расположено внутри грудной клетки. Такие явления связаны с распространением механических волн.
Механической волной называется процесс распространения колебаний в упругой среде, который сопровождается передачей энергии от одной точки среды к другой.
Механические волны не могут распространяться в вакууме.
Источником механических волн является колеблющееся тело. Если источник колеблется синусоидально, то и волна в упругой среде будет иметь форму синусоиды. Колебания, вызванные в каком-либо месте упругой среды, распространяются в ней с определенной скоростью, зависящей от плотности и упругих свойств среды.
Подчеркнем, что при распространении волны отсутствует перенос вещества, т. е. частицы колеблются вблизи положений равновесия. Среднее смещение частиц за большой промежуток времени равно нулю.
Рассмотрим основные характеристики волны.
Волновой фронт — это воображаемая поверхность, до которой дошло волновое возмущение в данный момент времени.
Линия, проведенная перпендикулярно волновому фронту в направлении распространения волны, называется лучом. Луч указывает направление распространения волны.
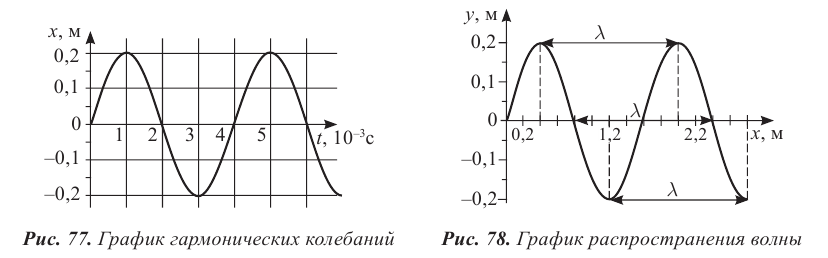
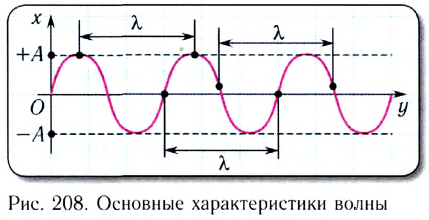
Основными характеристиками волны являются (рис. 208):
- амплитуда (A) — модуль максимального смещения точек среды из положений равновесия при колебаниях;
- период (T) — время полного колебания (период колебаний точек среды равен периоду колебаний источника волны);
- частота
— число полных колебаний в данной точке в единицу времени. Частота волн определяется частотой источника;
- скорость
— скорость перемещения гребня волны (это не скорость частиц!):
- длина волны
— наименьшее расстояние между двумя точками, колебания в которых происходят в одинаковой фазе, т. е. это расстояние, на которое волна распространяется за промежуток времени, равный периоду колебаний источника
Рассмотрим колебания источника волны, происходящие с циклической частотой 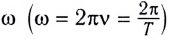
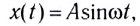
где x(t) — смещение источника от положения равновесия.
В некоторую точку среды колебания придут не мгновенно, а через промежуток времени, определяемый скоростью волны и расстоянием от источника до точки наблюдения. Если скорость волны в данной среде равна v, то зависимость от времени t координаты (смещения) х колеблющейся точки, находящейся на расстоянии r от источника, описывается функцией 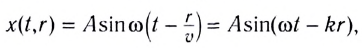
где k — волновое число 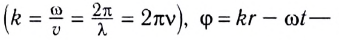
Выражение х(t, r) называется уравнением плоской волны, распространяющейся (бегущей) вдоль направления радиус-вектора
Бегущую волну можно наблюдать, проведя следующий опыт: если один конец резинового шнура, лежащего на гладком горизонтальном столе, закрепить и, слегка натянув шнур рукой, привести его второй конец в колебательное движение в направлении, перпендикулярном шнуру, то по нему побежит волна, описываемая уравнением плоской волны.
Рассмотрим классификацию бегущих волн по направлению колебаний частиц среды, в которой они распространяются.
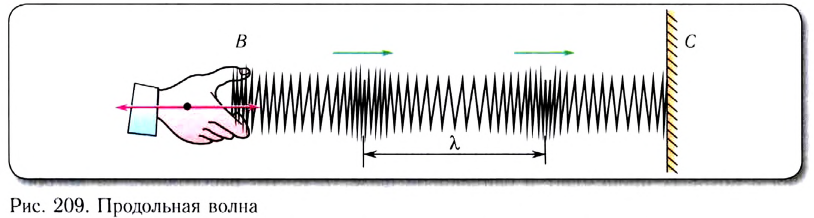
Волна называется продольной, если колебания частиц среды происходят вдоль направления распространения волн. Продольную волну легко получить с помощью длинной пружины, которая лежит на гладкой горизонтальной поверхности и один конец ее закреплен. Легким ударом по свободному концу В пружины мы вызовем появление волны (рис. 209).
При этом каждый виток пружины будет колебаться вдоль направления распространения волны ВС. Примерами продольных волн являются звуковые волны в воздухе и жидкости.
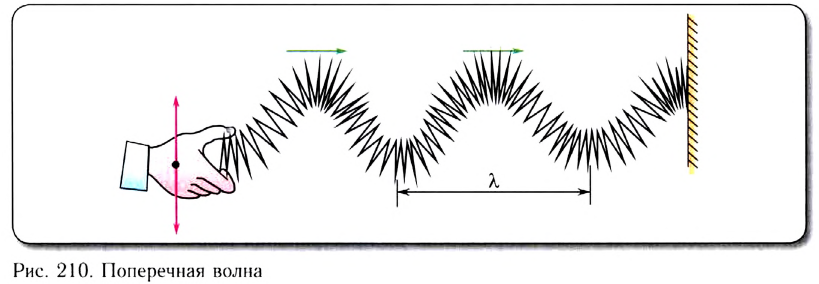
Волна называется поперечной, если частицы среды колеблются в плоскости, перпендикулярной направлению распространения волны. С помощью длинной пружины можно продемонстрировать распространение поперечных волн, если совершать колебания незакрепленного конца перпендикулярно пружине (рис. 210).
Поперечные волны вызывают звучание струн музыкальных инструментов при их возбуждении.
Продольные колебания симметричны относительно линии распространения ВС, и их действие на любой регистрирующий прибор не изменяется, если прибор будет поворачиваться вокруг направления распространения.
Действие поперечных волн на регистрирующий прибор зависит от того, в какой плоскости, проходящей через линию распространения, происходит колебание. Эта особенность поперечных волн носит название поляризации. Если колебания происходят в одной плоскости, то волну называют плоско или линейно поляризованной. Если конец вектора колебаний, например вектора смещения, скорости, напряженности электрического поля, описывает эллипс или окружность, то волну называют эллиптически или циркулярно-поляризованной.
До сих пор мы рассматривали волны, распространяющиеся в какой-либо среде. Волны, которые распространяются на границе раздела двух сред, называются поверхностными волнами. Примером данного типа волн служат волны на поверхности воды.
Звуковые волны. Скорость звука. Ультразвук
Звуком называются колебания среды, воспринимаемые органами слуха.
Раздел физики, в котором изучаются звуковые явления, называется акустикой.
Звуковая волна — упругая продольная волна, представляющая собой зоны сжатия и разрежения упругой среды (например, воздуха), распространяющиеся в пространстве с течением времени. Таким образом, в процессе распространения звуковой волны меняются такие характеристики среды, как давление и плотность.
Звуковые волны классифицируются по частоте следующим образом:
- инфразвук
- слышимый человеком звук
- ультразвук
- гиперзвук
Многие животные могут воспринимать ультразвуковые частоты. Например, собаки могут слышать звуки до 50 000 Гц, а летучие мыши — до 100 000 Гц. Инфразвук, распространяясь в воде на сотни километров, помогает китам и многим другим морским животным ориентироваться в толще воды.
Звуковые волны приносят человеку жизненно важную информацию — с их помощью мы общаемся, наслаждаемся мелодиями, узнаем по голосу знакомых людей. Мир окружающих нас звуков разнообразен и сложен, однако мы достаточно легко ориентируемся в нем и безошибочно можем отличить пение птиц от шума городской улицы.
Одной из важнейших характеристик звуковых волн является спектр. Спектром называется набор различных частот, образующих данный звуковой сигнал. Спектр может быть сплошным или дискретным.
В сплошном спектре присутствуют волны, частоты которых заполняют весь заданный спектральный диапазон.
В
дискретном спектре — конечное число волн с определенными частотами и амплитудами, которые образуют рассматриваемый сигнал.
По типу спектра звуки разделяются на шумы и музыкальные тона.
Шум — совокупность множества разнообразных кратковременных звуков (хруст, шелест, шорох, стук и т.п.) — представляет собой наложение большого числа колебаний с близкими амплитудами, но различными частотами (имеет сплошной спектр).
Музыкальный тон создается периодическими колебаниями звучащего тела (камертон, струна) и представляет собой гармоническое колебание одной частоты. На основе музыкальных тонов создана музыкальная азбука — ноты (до, ре, ми, фа, соль, ля, си), которые позволяют воспроизводить одну и ту же мелодию па различных музыкальных инструментах.
Музыкальный звук (созвучие) — результат наложения нескольких одновременно звучащих музыкальных тонов, из которых можно выделить
основной тон, соответствующий наименьшей частоте. Основной тон называется также первой гармоникой. Все остальные тоны называются обертонами. Обертоны называются гармоническими, если частоты обертонов кратны частоте основного тона. Таким образом, музыкальный звук имеет дискретный спектр.
Любой звук, помимо частоты, характеризуется интенсивностью.
Интенсивность I — это энергия 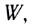
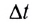
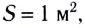
Другими словами, интенсивность любой волны — мощность, переносимая волной через единичную площадку, расположенную перпендикулярно к направлению распространения волны.
Единицей интенсивности в СИ является ватт на метр в квадрате 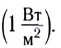
Чтобы вызвать звуковые ощущения, волна должна обладать некоторой минимальной интенсивностью, называемой порогом слышимости.
С возрастом порог слышимости человека возрастает.
Интенсивность звуковых волн, при которой возникает ощущение боли, называют порогом болевого ощущения или болевым порогом. Интенсивность звука, улавливаемого ухом человека, лежит в широких пределах: от 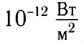
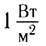
Реактивный самолет может создать звук интенсивностью 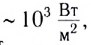
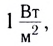
Уровни интенсивности звука L определяют обычно, используя шкалу, единицей которой является бел (Б) или, что гораздо чаще, децибел (дБ) (одна десятая бела). 1 Б самый слабый звук, который воспринимает наше ухо. Единица названа в честь изобретателя телефона А. Г. Белла. Измерение уровня интенсивности в децибелах проще, поэтому принято в физике и технике.
Уровень интенсивности L любого звука в децибелах вычисляется через интенсивность звука по формуле
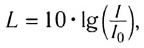
где I — интенсивность данного звука, 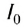
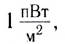
Так, поезд метро создает уровень интенсивности звука 100 дБ, мощные усилители — 120 дБ, а реактивный самолет — 150 дБ. Тем, кто при работе подвергается воздействию шума свыше 100 дБ, следует пользоваться наушниками.
Физическим характеристикам звука соответствуют определенные (субъективные) характеристики, связанные с восприятием его конкретным человеком. Это связано с тем, что восприятие звука — процесс не только
физический, но и физиологический. Действительно, человеческое ухо воспринимает звуковые колебания определенных частот и интенсивностей (это объективные, не зависящие от человека характеристики звука) по-разному, в зависимости от «характеристик приемника» (здесь влияют субъективные индивидуальные черты каждого человека).
Основными физиологическими характеристиками звука являются громкость, высота и тембр.
Громкость (степень слышимости звука) определяется как интенсивностью звука (амплитудой колебаний в звуковой волне), так и различной чувствительностью человеческого уха на разных частотах, т. е. его способностью улавливать звуки различных частот. Наибольшей чувствительностью человеческое ухо обладает в диапазоне частот от 1000 Гц до
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Волны. Основные понятия. Решение задач.Задача 1Скачать

Презентация по физике «Волны. Уравнение бегущей волны»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 2 500 дидактических материалов для школьного и домашнего обучения
Описание презентации по отдельным слайдам:
Тема урока:
МЕХАНИЧЕСКИЕ ВОЛНЫ.
Уравнение бегущей волны.
Волна- это процесс распространения колебаний в пространстве с течением времени.
Условия возникновения волны:
Механические волны могут распространяться только в какой- нибудь среде (веществе): в газе, в жидкости, в твердом теле. В вакууме механическая волна возникнуть не может.
Источником волн являются колеблющиеся тела, которые создают в окружающем пространстве деформацию среды.
Для возникновения механической волны необходимо:
1. Наличие упругой среды
2. Наличие источника колебаний – деформации среды
Волны бывают:
Поперечные – в которых колебания происходят перпендикулярно направлению движения волны.
Возникают только в твердых телах.
Распространение поперечных волн проиллюстрировано на рисунке:
Волны бывают:
2. Продольные
— в которых колебания происходят вдоль направления распространения волн.
Возникают в любой среде (жидкости, в газах, в тв. телах).
Типы волн
продольная
поперечная
Направление колебания
совпадает или противоположно
направлению распространения
волны
Направление колебания
перпендикулярно
направлению
распространения волны
Механические волны- это
процесс распространения колебаний в упругой среде;
при этом происходит перенос энергии от частицы к частице;
переноса вещества нет;
для создания механической волны необходима упругая среда: жидкость, твердое тело или газ.
ГДЕ КАКАЯ ВОЛНА?
ЭТО ИНТЕРЕСНО !
Волны на поверхности жидкости не являются ни продольными, ни поперечными. Если бросить на поверхность воды небольшой мяч, то можно увидеть, что он движется, покачиваясь на волнах, по круговой траектории. Таким образом, волна на поверхности жидкости представляет собой результат сложения продольного и поперечного движения частиц воды.
Сферическая волна
Волны на поверхности жидкости
Каждая волна распространяется с какой-то скоростью. Под скоростью волны понимают скорость распространения возмущения. Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую ее скорость изменяется.
Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.
Длина волны.
Длина поперечной и продольной волны.
Величины, характеризующие волну:
Характеристики волны:
Cкорость распространения волны – это..
[ ] = 1м/с
Период колебаний – это..
[ T ] = 1c
Частота колебаний
[ ] = 1 Гц
Энергия волны
Бегущая волна — волна, где происходит перенос энергии без переноса вещества.
Уравнение гарманической бегущей волны
Фотография механической волны
Узлы волны
Гребни волны
Ответьте на вопросы:
Что такое волна?
Условия возникновения волн?
Охарактеризуйте особенности колебаний точки в поперечной волне.
Какие типы волн вы знаете?
Может ли в воде распространяться поперечная волна?
На какое расстояние распространяется волна за время t = T/4?
Что называется длиной волны
Как связать скорость и длину волны?
Для чего служит уравнения бегущей волны?
СПАСИБО ЗА УРОК!
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 860 человек из 78 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Сейчас обучается 47 человек из 21 региона
Курс профессиональной переподготовки
Физика: теория и методика преподавания в образовательной организации
- Сейчас обучается 364 человека из 72 регионов
«Мотивация здорового образа жизни. Организация секций»
Свидетельство и скидка на обучение каждому участнику
- Для всех учеников 1-11 классов
и дошкольников - Интересные задания
по 16 предметам
«Как закрыть гештальт: практики и упражнения»
Свидетельство и скидка на обучение каждому участнику
Видео:🌊 Продольные и поперечные волны ⚛ ФизикаСкачать
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 845 227 материалов в базе
Ищем педагогов в команду «Инфоурок»
Другие материалы
- 31.03.2017
- 931
- 8
- 31.03.2017
- 590
- 2
- 31.03.2017
- 1553
- 71
- 31.03.2017
- 609
- 1
- 31.03.2017
- 1456
- 36
- 31.03.2017
- 471
- 0
- 31.03.2017
- 926
- 1
«Учись, играя: эффективное обучение иностранным языкам дошкольников»
Свидетельство и скидка на обучение
каждому участнику
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 31.03.2017 2823
- PPTX 3.4 мбайт
- 207 скачиваний
- Рейтинг: 5 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Богдашкина Елена Геннадьевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 6 месяцев
- Подписчики: 0
- Всего просмотров: 52367
- Всего материалов: 53
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Распространение волн в упругих средах. Звуковые волны | Физика 11 класс #18 | ИнфоурокСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу
Время чтения: 1 минута
Вузы РФ не будут повышать стоимость обучения на первом курсе
Время чтения: 1 минута
С 1 сентября в российских школах будут исполнять гимн России
Время чтения: 1 минута
Онлайн-семинар о здоровом образе жизни и организации секций
Время чтения: 2 минуты
Около 20% детей до 15 лет не воспринимают прочитанную информацию
Время чтения: 1 минута
Российские школьники начнут изучать историю с первого класса
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
💡 Видео
Урок 95 (осн). Механические волны. ЗвукСкачать

Лекция 2 ВолныСкачать

Физика 11 класс (Урок№10 - Электромагнитные волны.)Скачать

Механические волны. Физика 11 классСкачать

Стоячие волны. 11 класс.Скачать

Урок №45. Электромагнитные волны. Радиоволны.Скачать

Волновые свойства частиц. Волны де Бройля. 11 класс.Скачать

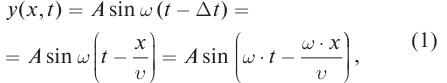
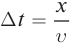


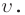
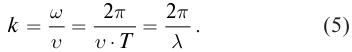
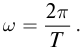
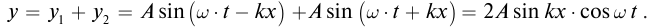
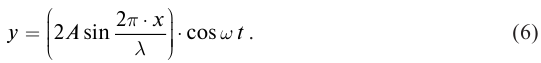
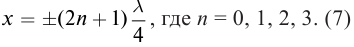


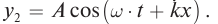
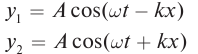
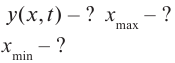
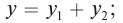
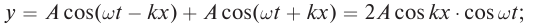
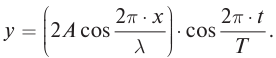
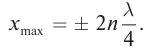
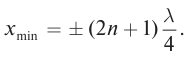
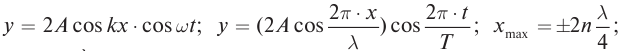
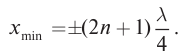

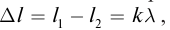

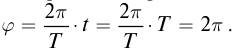

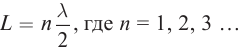


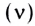 — число полных колебаний в данной точке в единицу времени. Частота волн определяется частотой источника;
— число полных колебаний в данной точке в единицу времени. Частота волн определяется частотой источника;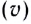 — скорость перемещения гребня волны (это не скорость частиц!):
— скорость перемещения гребня волны (это не скорость частиц!):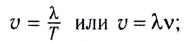
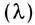 — наименьшее расстояние между двумя точками, колебания в которых происходят в одинаковой фазе, т. е. это расстояние, на которое волна распространяется за промежуток времени, равный периоду колебаний источника
— наименьшее расстояние между двумя точками, колебания в которых происходят в одинаковой фазе, т. е. это расстояние, на которое волна распространяется за промежуток времени, равный периоду колебаний источника