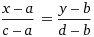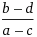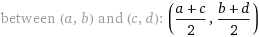Математика с WolframAlpha ® . Объяснения с примерами.
Прямая на плоскости в Wolfram|Alpha
Прямую на плоскости можно задать:
- двумя точками;
- точкой и направлением (угловым коэффициентом);
- отрезками на осях (точками пересечения с осями координат).
Соответственно, аналитическая геометрия рассматривает основные задачи на прямую на плоскости, связанные с этими способами.
Первая из этих основных задач: найти уравнение прямой, проходящей через две данные точки и построить эту прямую.
Традиционный способ решения задач аналитической геометрии состоит в использовании известных уравнений. Так, на плоскости уравнение прямой, проходящей через две данные точки c координатами (a, b) и (c, d) имеет вид:
Основные характеристики такой прямой можно вычислить по координатам данных точек. Например, точка пересечения с осью абсцисс (Ох), точка пересечения с осью ординат (Оу) и угловой коэффициент прямой (наклон прямой) вычисляются по формулам, соответственно:

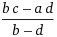
Расстояние между данными точками (a, b) и (c, d) вычисляется по формуле:
Координаты середины отрезка, соединяющего точки (a, b) и (c, d):
Wolfram|Alpha строит изображение прямой, проходящей через две данные точки, выводит уравнение этой прямой, а также все ее основные свойства по запросу
Отдельные свойства прямой, проходящей через две данные точки, можно получить по запросам:
Вторая задача — на уравнение прямой с угловым коэффициентом
Wolfram|Alpha «умеет» строить прямую по ее уравнению с угловым коэффициентом. Для этого нужно лишь задать параметры уравнения:
Третья задача — на уравнение прямой в отрезках на осях координат
Для построения прямой по ее уравнению в отрезках на осях координат Wolfram|Alpha использует такой запрос
Wolfram|Alpha может построить одновременно несколько прямых. Вот пара примеров:
Видео:Уравнение прямой по двум точкамСкачать

Вывести уравнение прямой по координатам двух точек
По введенным пользователем координатам двух точек вывести уравнение прямой, проходящей через эти точки.
Общее уравнение прямой имеет вид y = kx + b . Для какой-то конкретной прямой в уравнении коэффициенты k и b заменяются на числа, например, y = 4x — 2 . Задача сводится именно к нахождению этих коэффициентов.
Так как координаты точки это значения x и y , то мы имеем два уравнения. Пусть, например, координаты точки А(3;2), а координаты B(-1;-1). Получаем уравнения:
2 = k*3 + b,
-1 = k*(-1) + b.
Решая полученную систему уравнений находим значения k и b :
b = 2 — 3k
-1 = -k + 2 — 3k
4k = 3
k = 3/4 = 0.75
b = 2 — 3 * 0.75 = 2 — 2.25 = -0.25
Таким образом, получается уравнение конкретной прямой, проходящей через указанные точки: y = 0.75x — 0.25.
Алгоритм решения данной задаче на языке программирования будет таков:
- Получить значения координат первой точки и присвоить их переменным, например x1 и y1 .
- Получить значения координат ( x2, y2 ) второй точки.
- Вычислить значение k по формуле k = (y1 — y2) / (x1 — x2) .
- Вычислить значение b по формуле b = y2 — k * x2 .
- Вывести на экран полученное уравнение.
Видео:9 класс, 7 урок, Уравнение прямойСкачать

Уравнение прямой, проходящей через две точки онлайн
С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через две точки. Дается подробное решение с пояснениями. Для построения уравнения прямой задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точек в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Составляем уравнение прямой по точкамСкачать

Уравнение прямой, проходящей через две точки − примеры и решения
Пример 1. Построить прямую, проходящую через точки A(2, 1, 1), B(3, 1, -2).
 | (1) |
Подставив координаты точек A и B в уравнение (1), получим:
 |
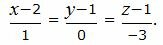 |
(Здесь 0 в знаменателе не означает деление на 0).
Составим параметрическое уравнение прямой:
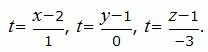 |
Выразим переменные x, y, z через параметр t :
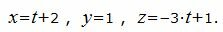 |
Каноническое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2) имеет следующий вид:
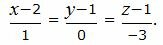 |
Параметрическое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2) имеет следующий вид:
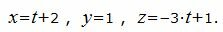 |
Пример 2. Построить прямую, проходящую через точки A(1, 1/5, 1) и B(−2, 1/2, −2).
 | (2) |
Подставив координаты точек A и B в уравнение (2), получим:
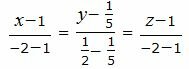 |
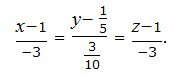 |
Составим параметрическое уравнение прямой:
 |
Выразим переменные x, y, z через параметр t :
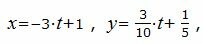 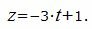 |
Каноническое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:
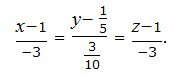 |
Параметрическое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:
🔥 Видео
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Видеоурок "Общее уравнение прямой"Скачать

УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Уравнение прямой. Урок 6. Геометрия 9 классСкачать

§51 Уравнение прямой в пространстве, проходящей через две точкиСкачать

Видеоурок "Уравнение прямой, проходящей через две точки"Скачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

11. Прямая в пространстве и ее уравненияСкачать

Математика это не ИсламСкачать

№972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2)Скачать

Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Видеоурок "Канонические уравнения прямой"Скачать

Уравнение прямой.Скачать