Вольфрам альфа приведение уравнения к каноническому виду (5 видео)

Квадратичная форма

$ mathbb A_ $ означает одно из множеств: $ mathbb Q_ $ рациональных, или $ mathbb R_ $ вещественных, или $ mathbb C_ $ комплексных чисел.

Содержание

Определение
Метод Лагранжа приведения квадратичной формы к каноническому виду
Матричная форма записи квадратичной формы
Метод Лагранжа и метод Гаусса
Формула Якоби
Закон инерции для квадратичных форм
Ранг квадратичной формы
Закон инерции
Конгруэнтность квадратичных форм
Знакоопределенность
Геометрия замен переменных
WolframAlpha по-русски
Приведение матрицы к ступенчатому виду: пошаговое решение в Wolfram|Alpha
Приведение к каноническому виду линейных уравнений с частными производными второго порядка
📸 Видео

Видео:53. Приведение общего уравнения кривой к каноническому видуСкачать

Определение

Квадратичной формой над множеством $ mathbb A_ $ называют однородный полином второй степени с коэффициентами из $ mathbb A_ $; если переменные обозначить $ x_1,dots,x_ $, то общий вид квадратичной формы от этих переменных: $$ f(x_1,dots,x_ )= sum_ f_x_jx_k= $$ $$begin displaystyle= f_x_1^2&+f_x_1x_2&+ dots & +f_x_1x_n+ \ &+f_x_2^2 &+ dots & +f_x_2x_n+ \ &+dots & & +dots + \ & & +f_x_jx_k & + dots+ \ & & &+f_x_n^2. end $$

Пример. Функции

$$x_1^2-x_1x_2+x_3^2 , , quad sqrt, x_2^2 — pi, x_3^2 , , quad -x_1x_2 , , quad mathbf i , x_1^2$$ являются квадратичными формами. Функции $$x_1^2-3, x_1+1 , , quad 5, x_1^2x_2^2 , , quad frac , , quad sqrt $$ не являются квадратичными формами.

Заметим, что в выражении для квадратичной формы присутствуют как квадраты переменных $ x_1^2,dots,x_n^2 $ так и их смешанные произведения $ x_j x_k $. Говорят, что квадратичная форма $ f(x_1,dots,x_ ) $ имеет канонический вид если $$f(x_1,dots,x_ )equiv f_x_1^2+f_x_2^2+dots+f_x_n^2 quad npu quad left<f_right>_^n subset mathbb A , $$ т.е. все коэффициенты при смешанных произведениях переменных равны нулю; в этом случае говорят также, что форма является «суммой квадратов» 1) .

Оказывается, что в любой квадратичной форме можно так сгруппировать входящие в нее одночлены, что в результате получится ее (эквивалентное) представление в виде суммы квадратов.

Пример.

$$ 2, x_1^2+4, x_1x_2 +x_2^2 equiv 2, (x_1+x_2)^2-x_2^2 equiv -2,x_1^2 + (2,x_1+x_2)^2 ; $$ $$ x_1^2+2 mathbf i x_1x_2 — x_2^2 equiv (x_1+ mathbf i x_2)^2 ; $$ $$-x_1^2+6,x_1x_2+6,x_1x_3+2,x_2^2+4,x_2x_3+2,x_3^2equiv $$ $$ equiv (x_1+x_2+x_3)^2-2,(x_1-x_2-x_3)^2+3,(x_2+x_3)^2 equiv $$ $$equiv -(x_1+3,x_2+3,x_3)^2+11,(x_2+x_3)^2 ; $$ $$ x_1x_2 equiv frac (x_1+x_2)^2- frac (x_1-x_2)^2 . $$

А в общем случае: $$ f(x_1,dots,x_ )equiv $$ $$ begin equiv a_1(c_x_1+c_x_2+dots+c_x_n)^2 +\ +a_2(c_x_1+c_x_2+dots+c_x_n)^2+ \ +dots+ \ +a_n(c_x_1+c_x_2+dots+c_x_n)^2 end $$ при $ _^n,<c_>_^n $ — константах. Такое представление оказывается достаточно удобным для анализа квадратичной формы — например, в случае вещественных форм, при проверке выполнимости неравенства вида $ f(x_1,dots,x_ ) ge 0 $. Приведенные выше примеры показывают неоднозначность представления в виде суммы квадратов: вид квадратов и даже их количество для одной и той же формы могут быть различными. С целью обеспечения частичной унификации установим некоторое дополнительное ограничение, а именно, потребуем, чтобы линейные однородные формы $$ c_x_1+c_x_2+dots+c_x_n, c_x_1+c_x_2+dots+c_x_n,dots, c_x_1+c_x_2+dots+c_x_n $$ были линейно независимыми. При таком ограничении любое представление квадратичной формы в виде суммы квадратов называется каноническим видом квадратичной формы.

Задача. Для произвольной квадратичной формы $ f(x_1,dots,x_ ) $ построить (хотя бы один) ее канонический вид.

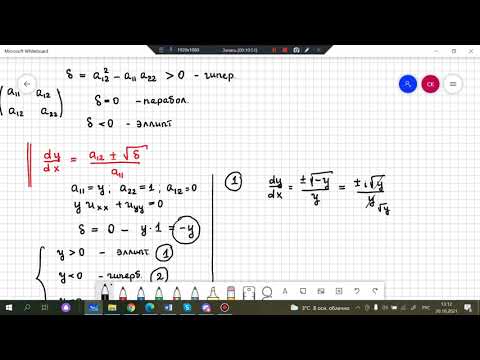
$$ x^2 -2,xy+3,y^2+x-4,y-15=0 $$ определить к какому типу (эллипс, гипербола, парабола,…) она относится.

Видео:§31.1 Приведение уравнения кривой к каноническому виду Скачать

Метод Лагранжа приведения квадратичной формы к каноническому виду

Существует универсальный алгоритм, приводящий произвольную квадратичную форму к каноническому виду.

1. Пусть $ f_ne 0 $. Выделим в $ f(x_1,dots, x_n)_ $ все слагаемые, содержащие $ x_ $: $$ f_x_1^2+f_x_1x_2+ dots +f_x_1x_n+ sum_ f_x_jx_k = $$ $$ = f_left(x_1^2+frac<f_><f_>x_1x_2+dots+ frac<f_><f_>x_1x_n right)+dots= $$ $$ =f_left[ left(x_1+frac<f_><2f_>x_2+dots+ frac<f_><2f_>x_n right)^2-left(frac<f_><2f_>x_2+dots+ frac<f_><2f_>x_n right)^2 right]+dots= $$ $$ =f_ left(x_1+frac<f_><2f_>x_2+dots+ frac<f_><2f_>x_n right)^2 — f_left(frac<f_><2f_>x_2+dots+ frac<f_><2f_>x_n right)^2 +dots $$ В последнем представлении первое слагаемое представляет собой квадрат линейной формы по переменным $ x_,x_2,dots,x_n $; все оставшиеся слагаемые не зависят от $ x_ $, т.е. составляют квадратичную форму от переменных $ x_,dots,x_n $. Таким образом, исходная задача для формы $ n_ $ переменных оказывается сведенной к случаю формы $ (n-1)_ $-й переменной; последняя преобразуется по аналогичному принципу.

2. Если $ f_=0 $, но $ exists k: f_ne 0 $, т.е. при хотя бы одном квадрате переменной коэффициент отличен от нуля. Алгоритм модифицируется таким образом, что выделение полного квадрата начинается с переменной $ x_ $ вместо $ x_ $ — первая ничем не лучше (и не хуже) $ k_ $-й!

3. Совсем исключительный случай: квадраты переменных вообще отсутствуют, т.е. $ f_=dots=f_=0 $. Выбираем один из ненулевых коэффициентов при смешанных произведениях переменных: пусть $ f_ne 0 $. Представляем $ x_k=(x_j+x_k)-x_j $ и заменяем все вхождения переменной $ x_ $ на $ X_k-x_j $ при вспомогательной переменной $ X_k=x_j+x_k $. В новой квадратичной форме уже присутствует квадрат переменной $ x_ $ с ненулевым коэффициентом. Тем самым этот случай сводится к предыдущему. После приведения новой формы к сумме квадратов возвращаемся к «старой» переменной $ x_ $.

Пример. Привести форму

$$ f=4,x_1^2+2,x_2^2+x_3^2+x_4^2-4,x_1x_2-4,x_1x_3+4,x_1x_4+4,x_2x_3-4,x_3x_4 $$ к каноническому виду.

Решение. $$ begin f&=&4left(x_1^2-x_1x_2-x_1x_3+x_1x_4right)+2x_2^2+x_3^2+x_4^2+4x_2x_3-4x_3x_4=\ &=&4bigg[ left(x_1-frac, x_2-frac,x_3+ frac,x_4, right)^2- left(-frac, x_2-frac, x_3+frac, x_4right)^2 bigg] + \ &+&2,x_2^2+x_3^2+x_4^2+4,x_2x_3-4,x_3x_4= \ &=&4,left(x_1-frac, x_2-frac,x_3+ frac,x_4, right)^2+\ & & + Big[left(x_2+x_3+x_4, right)^2- left(x_3+x_4 right)^2Big]-2,x_3x_4 = \ &=&4,left(x_1-frac, x_2-frac,x_3+ frac,x_4, right)^2+ left(x_2+x_3+x_4, right)^2- \ &&-x_3^2-4,x_3x_4-x_4^2= \ && 4,left(x_1-frac, x_2-frac,x_3+ frac,x_4, right)^2+ left(x_2+x_3+x_4, right)^2- \ &&-Big[ left(x_3+ 2, x_4, right)^2-4, x_4^2Big] -x_4^2 = \ &=&4,left(x_1-frac, x_2-frac,x_3+ frac,x_4, right)^2+ left(x_2+x_3+x_4, right)^2-left(x_3+ 2, x_4, right)^2+3,x_4^2 end $$

Ответ. $ fequiv 4,left(x_1-frac, x_2-frac,x_3+ frac,x_4, right)^2+ left(x_2+x_3+x_4, right)^2-left(x_3+ 2, x_4, right)^2+3,x_4^2 $.

Пример. Привести форму

$$ f=x_1^2+x_2^2-4,x_3^2+2,x_1x_2+6,x_1x_3+4,x_2x_3 $$ к каноническому виду.

Решение. $$ fequiv (x_1+x_2+3,x_3)^2-(x_2+3,x_3)^2+x_2^2-4,x_3^2+4,x_2x_3 equiv $$ $$ equiv (x_1+x_2+3,x_3)^2-2,x_2x_3 -13,x_3^2 equiv $$ В соответствии с алгоритмом, на следующем шаге нужно выделять слагаемые, содержащие переменную $ x_ $, но коэффициент при $ x_2^2 $ в правой части формулы обратился в нуль. Поэтому — в соответствии с пунктом 2 метода — приходится выделять квадрат на основе переменной $ x_ $: $$ (x_1+x_2+3,x_3)^2-13, left(x_3-fracx_2right)^2+13cdot fracx_2^2 . $$

Ответ. $ (x_1+x_2+3,x_3)^2-13, left(x_3-fracx_2right)^2+ fracx_2^2 $.

Пример. Привести форму

$$ f=x_1x_2-3,x_1x_3+2,x_2x_3 $$ к каноническому виду.

Решение. Коэффициенты при квадратах переменных все равны нулю. Действуем в соответствии с пунктом 3 метода Лагранжа. Поскольку коэффициент при $ x_1x_2 $ отличен от нуля, делаем замену переменной $ x_2=X_2-x_1 $ при $ X_2=x_1+x_2 $: $$ fequiv -x_1^2+x_1X_2-5,x_1x_3+2,X_2x_3 . $$ Дальнейший ход решения — в соответствии с пунктом 1 метода Лагранжа: $$ -left(x_1-fracX_2+fracx_3right)^2+left(-fracX_2+fracx_3right)^2+2,X_2x_3 equiv $$ $$ equiv -left(x_1-fracX_2+fracx_3right)^2+fracX_2^2-fracX_2x_3+fracx_3^2 equiv $$ $$ equiv -left(x_1-fracX_2+fracx_3right)^2+fracleft(X_2-x_3 right)^2+6,x_3^2 $$ Получили сумму квадратов форм от переменных $ x_1,X_2,x_3 $. Возвращаемся к переменной $ x_ $:

Ответ. $ -(fracx_1-fracx_2+fracx_3)^2+frac(x_1+x_2-x_3)^2+6,x_3^2 $.

Видео:УМФ, 20.10.2021, приведение уравнений к каноническому видуСкачать

Матричная форма записи квадратичной формы

Задача. Установить правило формирования коэффициентов канонического вида квадратичной формы, получающегося применением метода Лагранжа.

Прежде всего, соберем все переменные в один вектор, а вернее — в два вектора: $$ _ mbox X= left(begin x_1 \ vdots \ x_n end right) quad mbox X^ = (x_1,dots,x_n) ; $$ здесь $ ^ $ означает транспонирование. Не очень принципиально, что обозначать через $ X_ $ — столбец или строку; и хотя сокращение $ f(x_1,dots,x_n)=f(X) $ кажется не вполне корректным с точки зрения только что введенного обозначения, тем не менее не будем навешивать в правую часть дополнительные значки…

Если определить верхнетреугольную матрицу $ mathbf F $ равенством: $$ = left( begin f_&f_&dots &f_ \ &f_& dots & f_ \ mathbb O & &ddots & vdots \ & & & f_ end right), $$ то квадратичную форму можно записать в виде произведения трех матриц $$ _ mbox times mbox times mbox $$ $$ f(X)=X^ X .$$ Более того, можно написать бесконечно много подобных представлений для одной и той же квадратичной формы $ f_ $, подбирая разные матрицы

Пример. $ f=x_1^2+x_2^2-4,x_3^2+2,x_1x_2+6,x_1x_3+4,x_2x_3 equiv $

$$ equiv (x_1,x_2,x_3) left( begin 1 & 2 & 6 \ 0 & 1 & 4 \ 0 & 0 & -4 end right) left( begin x_1 \ x_2 \ x_3 end right) equiv (x_1,x_2,x_3) left( begin 1 & 0 & 3 \ 2 & 1 & 4 \ 3 & 0 & -4 end right) left( begin x_1 \ x_2 \ x_3 end right)equiv $$ $$ equiv (x_1,x_2,x_3) left( begin 1 & 1 & 3 \ 1 & 1 & 2 \ 3 & 2 & -4 end right) left( begin x_1 \ x_2 \ x_3 end right)equiv dots $$

Пример. Для приведенной выше квадратичной формы

$$ f=x_1^2+x_2^2-4,x_3^2+2,x_1x_2+6,x_1x_3+4,x_2x_3 $$ ее правильной записью будет именно последняя:

$$ fequiv (x_1,x_2,x_3) left( begin 1 & 1 & 3 \ 1 & 1 & 2 \ 3 & 2 & -4 end right) left( begin x_1 \ x_2 \ x_3 end right) $$ Правило формирования матрицы довольно просты: на диагонали ставятся коэффициенты при квадратах, а внедиагональные элементы получаются располовиниванием коэффициентов при смешанных произведениях переменных.

$ x_ $	$ x_ $	$ x_ $
$ x_ $	$ f_ $	$ fracf_ $	$ fracf_ $
$ x_ $	$ fracf_ $	$ f_ $	$ fracf_ $
$ x_ $	$ fracf_ $	$ fracf_ $	$ f_ $

Пример. Для

$$ f(x_1,x_2)=a_x_1^2+2, a_x_1x_2+a_x_2^2 $$ имеем: $$ = left( begin a_ & a_ \ a_ & a_ end right) ; (f)=a_a_-a_^2 ; $$ последнее выражение вполне напоминает дискриминант квадратного трехчлена $ a_x^2+2, a_x+a_ $ и это обстоятельство оправдывает использование слова дискриминант для нового объекта…

Рассмотрим замены переменных в квадратичной форме, т.е. переход от переменных $ x_,dots,x_ $ к новым переменным $ y_,dots,y_ $. Ограничимся только линейными заменами вида $$ left< begin x_1&=&c_y_1+c_y_2+dots+c_y_n, \ x_2&=&c_y_1+c_y_2+dots+c_y_n, \ dots & & dots \ x_n&=&c_y_1+c_y_2+dots+c_y_n. end right. $$ Результатом такой замены переменных будет новая квадратичная форма относительно новых переменных. Установим по какому закону формируются ее коэффициенты. С этой целью введем в рассмотрение матрицу замены переменных $$ C= left( begin c_ & c_ & dots & c_ \ c_ & c_ & dots & c_ \ dots & & & dots \ c_ & c_ & dots & c_ \ end right) ; $$ которая позволяет переписать саму замену переменных в матричном виде $$ left(begin x_1 \ x_2 \ vdots \ x_n end right)= left( begin c_ & c_ & dots & c_ \ c_ & c_ & dots & c_ \ dots & & & dots \ c_ & c_ & dots & c_ \ end right) left(begin y_1 \ y_2 \ vdots \ y_n end right) qquad iff qquad X=CY . $$ Тогда формальная подстановка последнего варианта в правильную запись квадратичной формы приведет к следующей цепочке $$ f(X)=X^X= (CY)^ (CY)=Y^ C^C Y=tilde f (Y) , $$ (здесь использовались некоторые свойства операции транспонирования ) и, если обозначить матрицу $$ mathbf B =C^C , $$ то мы получаем правило формирования матрицы квадратичной формы, получившейся в результате замены переменных, с помощью операции произведения матриц. Обратим внимание на еще один факт — матрица $ mathbf B $ является симметричной: $$ mathbf B^ =(C^C)^= C^^left(C^ right)^ = C^C= mathbf B , $$ т.е. выбор в качестве матричной записи квадратичной формы именно того варианта, что основан на симметричной матрице, позволяет сохранить это свойство при любой линейной замене переменных.

Задача о нахождении канонического вида квадратичной формы $ X^X $ может быть также переформулирована в терминах замены переменных: требуется найти такую матрицу $ C_ $, чтобы матрица $ mathbf B= C^C $ оказалась диагональной: $$ mathbf B= left( begin a_ & & & \ & a_ & & \ & & ddots & \ & & & a_ end right) ; $$ при этом дополнительным условием ставится невырожденность (неособенность) матрицы $ C_ $: $$ det C ne 0 . $$

Теорема. Для любой квадратичной формы над $ mathbb A $ существует невырожденная линейная замена переменных $ X=CY $ такая, что преобразованная квадратичная форма $ widetilde f(Y) $ имеет канонический вид.

Вернемся к примерам предыдущего пункта, перепишем их на матричном языке.

Пример. Для формы

$$ f(x_1,x_2,x_3,x_4)= $$ $$=4,x_1^2+2,x_2^2+x_3^2+x_4^2-4,x_1x_2-4,x_1x_3+4,x_1x_4+4,x_2x_3-4,x_3x_4 $$ замена переменных осуществляется формулами

$$ begin y_1=& x_1 &-frac, x_2&-frac,x_3&+ frac,x_4, \ y_2=& & x_2&+x_3&+x_4, \ y_3=& & & x_3 &+ 2, x_4,\ y_4=& &&& x_4, end $$ т.е. матрица замены переменных $$ C= left( begin 1 & -frac & -frac & frac \ 0 & 1 & 1 & 1 \ 0 & 0 & 1 & 2 \ 0 & 0 & 0 & 1 end right) $$ имеет верхнетреугольный вид. Канонический вид в новых переменных записывается $$ f(x_1,x_2,x_3,x_4) equiv 4,y_1^2+y_2^2-y_3^2+3,y_4^2 . $$

Для формы $$ f(x_1,x_2,x_3)=x_1^2+x_2^2-4,x_3^2+2,x_1x_2+6,x_1x_3+4,x_2x_3 $$ замена переменных уже не имеет треугольного вида: $$ begin y_1=& x_1 &+ x_2&+3,x_3 \ y_2=& & -fracx_2&+x_3 \ y_3=& & fracx_2 & end qquad iff qquad C= left( begin 1 & 1 & 3 \ 0 & -frac & 1 \ 0 & frac & 0 end right) . $$ Для формы $$ f(x_1,x_2,x_3)=x_1x_2-3,x_1x_3+2,x_2x_3 $$ получили: $$ begin y_1=& fracx_1 &-fracx_2&+fracx_3 \ y_2=& x_1&+x_2&-x_3 \ y_3=& & & x_3 end qquad iff qquad C= left( begin frac & -frac & frac \ 1 & 1 & -1 \ 0 & 1 & 1 end right) , $$ т.е. замена переменных также не имеет треугольного вида. ♦

Поставленную в начале пункта задачу об установлении структуры канонического вида квадратичной формы попытаемся решить сначала для случая когда замену переменных можно подобрать именно в треугольном виде.

Видео:Семинар 6. Приведение уравнения кривой II порядка к каноническому видуСкачать

Метод Лагранжа и метод Гаусса

Пример. Рассмотрим матрицу квадратичной формы

из предыдущих пунктов, и, временно выходя из круга поставленных в настоящем разделе задач, попробуем применить к ней метод Гаусса приведения к треугольному виду: $$ left( begin 4 & -2 & -2 & 2 \ -2 & 2 & 2 & 0 \ -2 & 2 & 1 & -2 \ 2 & 0 & -2 & 1 end right) rightarrow left( begin 4 & -2 & -2 & 2 \ 0 & 1 & 1 & 1 \ 0 & 1 & 0 & -1 \ 0 & 1 & -1 & 0 end right) rightarrow $$ $$ rightarrow left( begin 4 & -2 & -2 & 2 \ 0 & 1 & 1 & 1 \ 0 & 0 & -1 & -2 \ 0 & 0 & -2 & -1 end right) rightarrow left( begin 4 & -2 & -2 & 2 \ 0 & 1 & 1 & 1 \ 0 & 0 & -1 & -2 \ 0 & 0 & 0 & 3 end right) . $$ Обратим внимание на два обстоятельства: диагональные элементы последней матрицы совпадают с коэффициентами канонического вида квадратичной формы, а коэффициенты замены переменных, приводящей к этому каноническому виду, совпадают с элементами строк этой матрицы, если их разделить на соответствующие диагональные элементы. Возникает подозрение , что метод Лагранжа является «замаскированной» версией метода Гаусса. ♦

Для того, чтобы выяснить аналитический смысл преобразований по методу Лагранжа найдем правило формирования коэффициентов в первом шаге приведения квадратичной формы к каноническому виду. Пусть исходная квадратичная форма записана в виде $$ f(x_1,dots,x_ )=sum_ a_x_jx_k= $$ $$ begin = a_x_1^2&+2a_x_1x_2&+ dots & +2a_x_1x_n+ \ &+a_x_2^2 &+ dots & +2a_x_2x_n+ \ & & +dots & + \ & & &+a_x_n^2, end $$ т.е. коэффициенты при смешанных произведениях переменных записаны с выделением множителя $ 2_ $. После выделения полного квадрата, содержащего переменные $ x_1,x_2,dots,x_n $: $$ f(x_1,x_2,dots,x_n)equiv a_ left(x_1+frac<a_><a_>x_2+dots+ frac<a_><a_>x_n right)^2 + f_2(x_2,dots,x_n) $$ в правой части тождества образовалась квадратичная форма $ f_ $, не содержащая $ x_ $. Она равна $$ f_2 =sum_ a_x_jx_k- a_left(frac<a_><a_>x_2+dots+ frac<a_><a_>x_n right)^2= $$ $$ =sum_ a_x_jx_k-a_sum_ frac<a_a_><a_^2>x_jx_k= sum_left( a_-frac<a_><a_>a_ right) x_jx_k . $$ Если теперь выписать матрицу этой квадратичной формы (она имеет порядок $ n_-1 $), то ее элементы образуются по точно такому же правилу, как и коэффициенты матрицы, получающейся из матрицы $ mathbf A_ $ в результате первого шага метода Гаусса.

Теорема. Метод Лагранжа приведения квадратичной формы $ X^X $ к каноническому виду эквивалентен методу Гаусса приведения матрицы $ $ к треугольному виду.

Доказательство. Действительно, первый шаг прямого хода метода исключения переменных Гаусса преобразует матрицу $ mathbf A $ следующим образом: $$ left( begin a_& a_& a_& dots & a_ \ a_& a_& a_& dots & a_ \ & dots & & dots & \ a_& a_& a_& dots & a_ end right) rightarrow left(begin a_&a_&dots&a_\ 0&a_^& dots &a_^\ &dots & & dots \ 0&a_^&dots &a_^ end right) ; $$ здесь $$a_^ = a_ — frac<a_a_><a_> ,$$ и предполагается, что $ a_ne 0 $. Видим, что формула формирования элементов матрицы $$ left(begin a_^& dots&a_^\ dots & & dots & \ a_^&dots &a_^ end right)_ $$ точно такая же, как и матрицы квадратичной формы $ f_2 $. Более того, поскольку матрица $ $ симметрична ($ a_=a_ $), то и только что полученная матрица оказывается симметричной. Если $ a_^ ne 0 $, то к этой новой матрице можно снова применить ту же процедуру, и т.д., и в конце концов придем к матрице первого порядка. Собирая все промежуточные результаты в одну матрицу, получим ее в треугольном виде $$ left(begin a_&a_&dots&a_ &a_\ 0&a_^& dots&a_^ &a_^\ & & ddots & & dots \ 0 &0 & &a_^&a_^ \ 0 &0 &dots & 0 &a_^ end right) $$ при условии, что ни одно из чисел на диагонали не обратилось в нуль: $$a_ ne 0, a_^ ne 0, dots, a_^ ne 0, a_^ ne 0 .$$ Если теперь обратиться к методу Лагранжа, то увидим, что полученная матрица как раз и определяет замену переменных $$ left<begin y_1=&displaystyle x_1+&frac<a_><a_>x_2+&dots+&frac<a_><a_>x_+& frac<a_><a_>x_n \ y_2=&displaystyle &x_2+&dots + &frac<a_^><a_^>x_+& frac<a_^><a_^>x_ \ vdots & & & ddots & dots & \ y_=&displaystyle & & &x_+ &frac<a_^><a_^>x_n \ y_n=&&&&&x_n end right. , $$ приводящую квадратичную форму к каноническому виду: $$ a_y_1^2 + a_^ y_2^2 + dots +a_^ y_^2 + a_^ y_n^2 . $$ ♦

Видео:2. Приведение уравнений второго порядка к каноническому видуСкачать

Формула Якоби

Теорема [Якоби]. Квадратичная форма $ f(X)=X^X $ с симметричной матрицей $ $, ранг которой равен $ mathfrak r_ $, а главные миноры $ _^ $ отличны от нуля, приводится к следующему каноническому виду (формула Якоби 3) ):

$$ frac +frac +frac +dots+frac<z_^2><det mathbf A_<-1> cdot det mathbf A_> $$ Здесь $$ z_1 =frac partial f / partial x_1, z_2= frac left| begin a_ & partial f / partial x_1 \ a_ & partial f / partial x_2 end right|, z_3= frac left| begin a_ & a_ & partial f / partial x_1 \ a_ & a_ & partial f / partial x_2 \ a_ & a_ & partial f / partial x_3 end right|, dots , $$ $$ qquad qquad z_= frac left| begin a_ & a_ & dots & a_ & partial f / partial x_1 \ a_ & a_ & dots & a_ & partial f / partial x_2 \ dots & & & dots & dots \ a_ & a_ & dots & a_ & partial f / partial x_ end right| $$

Пример. Для квадратичной формы $$ f(x_1,x_2,x_3,x_4)= $$

Легко убедиться, что это — проявление общего правила. Выражение для $$ z_= frac left| begin a_ & a_ & dots & a_ & partial f / partial x_1 \ a_ & a_ & dots & a_ & partial f / partial x_2 \ dots & & & dots & dots \ a_ & a_ & dots & a_ & partial f / partial x_ end right| $$ при $ k in $ преобразуем следующим образом: из последнего столбца определителя $$ = left| begin a_ & a_ & dots & a_ & a_x_1+a_x_2+dots+ a_ x_+a_x_k+dots+a_x_n \ a_ & a_ & dots & a_ & a_x_1+a_x_2+dots+ a_ x_+a_x_k+dots+a_x_n \ dots & & & dots & dots \ a_ & a_ & dots & a_ & a_x_1+a_x_2+dots+ a_ x_+a_x_k+dots+a_x_n end right| $$ вычтем первый, домноженный на $ x_1 $, второй, домноженный на $ x_2 $, и т.д., $ (k-1) $-й, домноженный на $ x_ $. В результате получим линейную форму $$ z_k= left| begin a_ & a_ & dots & a_ & a_ \ a_ & a_ & dots & a_ & a_ \ dots & & & dots & dots \ a_ & a_ & dots & a_ & a_ end right|x_k + dots + left| begin a_ & a_ & dots & a_ & a_ \ a_ & a_ & dots & a_ & a_ \ dots & & & dots & dots \ a_ & a_ & dots & a_ & a_ end right|x_n , , $$ не зависящую от $ x_1,dots, x_ $. Коэффициент же при $ x_k $ равен $ det mathbf A_k $ и отличен от нуля по условию теоремы. Если его вынести за пределы формы, то получим еще альтернативный вариант формулы Якоби.

Квадратичная форма $ f(X)=X^X $ с симметричной матрицей $ $, ранг которой равен $ mathfrak r_ $, а главные миноры $ _^ $ отличны от нуля, приводится к следующему каноническому виду:

$$ y_1^2 det mathbf A_1 + y_2^2frac +y_3^2frac +dots+y_^2 frac<det mathbf A_><det mathbf A_> ; $$ при этом линейные относительно переменных $ x_1,dots,x_n $ формы $ _^ $ выражаются по формулам $$ left< begin y_1=&displaystyle x_1+&tilde c_x_2& &+dots+&tilde c_x_+&tilde c_x_n \ y_2=&displaystyle &x_2+& & dots + &tilde c_x_+&tilde c_x_ \ vdots & & & ddots & & dots & \ y_=&displaystyle & & &x_+ & dots + & tilde c_x_n end right. $$ Здесь $$ tilde c_=a_/a_, tilde c_=left| begin a_ & a_ & dots & a_ & a_ \ a_ & a_ & dots & a_ & a_ \ dots & & & dots & dots \ a_ & a_ & dots & a_ & a_ end right| Bigg/ det mathbf A_j , . $$

При $ mathfrak r = n $ матрица $ tilde C_ $ из предыдущей формулы становится верхнетреугольной: $$ Y=tilde C X , ; $$ при этом на главной диагонали будут стоять $ 1 $. Обратная к матрице такого вида имеет ту же структуру — и матрица $ C=tilde C^ $ является матрицей, которая встретилась нам в предыдущем ПУНКТЕ.

Теорема. Квадратичная форма $ f(X)=X^X $ при симметричной неособенной матрице $ $ приводится к каноническому виду заменой переменных, задаваемой верхней унитреугольной матрицей

$$ X=CY quad npu C= left( begin 1& c_& dots & c_ \ & 1& dots & c_ \ mathbb O & & ddots & vdots \ & & & 1 end right) $$ тогда и только тогда, когда все главные миноры матрицы $ $ отличны от нуля. Этот канонический вид представлен формулой Якоби $$ y_1^2 det mathbf A_1 + y_2^2frac +dots+y_^2 frac<det mathbf A_><det mathbf A_> . $$ Доказательство достаточности условия теоремы уже произведено, необходимость доказывается в пункте ☞ LDU-разложение матрицы.

Видео:Wolframalpha : решение любых задач для студента по алгебре, вышке, физике, дифференциальные ур. и прСкачать

Закон инерции для квадратичных форм

Для заданной квадратичной формы канонические виды, т.е. представления в виде сумм квадратов, можно построить разными способами. Выясним, какие характеристики являются общими (инвариантными) для этих представлений.

Видео:Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать

Ранг квадратичной формы

Предположим, что с помощью какой-либо невырожденной замены переменных мы привели квадратичную форму к каноническому виду: $$widetilde f(Y)=alpha_1y_1^2+dots+alpha_n y_n^2 .$$ Может так случиться, что часть коэффициентов $ _^n $ обратится в нуль.

Рангом квадратичной формы называется ранг ее матрицы: $$operatorname ( f ) = operatorname ( ) .$$

Теорема. Ранг квадратичной формы не меняется при невырожденных заменах переменных:

$$ operatorname (f) = operatorname( C^C ) quad npu quad forall C, det C ne 0 .$$

Доказательство основано на следствии к теореме $ 2 $, приведенной ☞ ЗДЕСЬ: ранг матрицы не меняется при домножении ее на произвольную неособенную.

Ранг квадратичной формы равен числу ненулевых коэффициентов в ее каноническом виде.

Видео:Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Закон инерции

Число положительных (или отрицательных) коэффициентов в каноническом виде квадратичной формы $ f_(X) $ называется ее положительным (соответственно, отрицательным) индексом инерции. Буду обозначать эти индексы 4) $$n_(f) quad mbox quad n_(f) . $$ Разность 5) $$sigma (f) = n_(f)-n_(f)$$ называется сигнатурой квадратичной формы (а также сигнатурой соответствующей ей симметричной матрицы).

Теорема [закон инерции]. Индексы инерции не зависят от способа приведения квадратичной формы к каноническому виду.

Доказательство ☞ ЗДЕСЬ.

Пример. Найти ранг и сигнатуру квадратичной формы $ f(x_1,x_2,x_3)=x_1x_2-x_2x_3 $.

Решение. Приводим квадратичную форму к каноническому виду по методу Лагранжа: $$f=frac ,(x_1+x_2-x_3)^2 — frac ,(x_1-x_2-x_3)^2 .$$

Ответ. $ operatorname (f) = 2,, sigma (f)=0 $.

В предположении, что ранг матрицы $ mathbf A_ $ равен $ mathfrak r_ $, а ее главные миноры $ < det _j >_^ $ отличны от нуля, имеем:

$$ n_(f)=(1,det _1,dots, det _), n_(f)=(1,det _1,dots, det _) . $$ Здесь $ _ $ — число знакопостоянств, а $ _ $ — число число знакоперемен в последовательности. Для сигнатуры квадратичой формы также справедлива и формула $$ sigma (f)= sum_^ operatorname (det (mathbf A_) cdot det (mathbf A_) ) quad npu quad det (mathbf A_)=1 $$ и операции $ operatorname $ определения знака, введенной ☞ ЗДЕСЬ.

Доказательство следует из формулы Якоби.

Правило вычисления сигнатуры из предыдущей теоремы остается справедливым и в случае, если в последовательности главных миноров $ < det _j >_^ $ имеются нулевые, но не подряд идущие, и $ det _ ne 0 $. Если, например,

$$ det (mathbf A_) = 0, det (mathbf A_) ne 0, det (mathbf A_) ne 0 quad npu quad jin<1,dots, -1> ,$$ то сумма $$ operatorname (det (mathbf A_) cdot det (mathbf A_) )+ operatorname (det (mathbf A_) cdot det (mathbf A_) ) $$ считается равной нулю. (Можно также доказать, что в этом случае главные миноры $ det (mathbf A_) $ и $ det (mathbf A_) $ имеют противоположные знаки.)

Пример. Найти ранг и сигнатуру квадратичной формы

$$f_ <<coloralpha >>(x_1,x_2,x_3)=3,x_1^2 -4,x_1x_2-2,x_1x_3 + <coloralpha > , x_2^2 +6, x_2x_3 $$ в зависимости от значений параметра $ <coloralpha > $.

Решение. Сначала пробуем применить формулу из последнего следствия: $$det _1=3, det _2=3, <coloralpha > -4, det _3= det =- <coloralpha > -15 .$$ При $ <coloralpha > notin $ формула применима при $ =3 $: $$n_(f)=left< begin 2 & npu & <coloralpha > >4/3 ;\ 2 & npu & -15 -15 & 3 & 1 end $$

Рассмотренный только что пример относится к общей задаче оценки влияния параметров на характеристики квадратичной формы:

Как меняются ранг и сигнатура при непрерывном изменении параметров?

Пусть квадратичная форма зависит от параметров $ alpha, beta, dots $, причем эта зависимость — полиномиальная. Пусть при некотором наборе вещественных значений параметров все главные миноры матрицы квадратичной формы отличны от нуля. Тогда ранг и сигнатура квадратичной формы могут быть вполне определены знаками этих миноров посредством формулы из следствия к закону инерции. Поскольку элементы миноров полиномиально зависят от параметров, то мы получаем систему неравенств, которую (при необходимости домножением некоторых неравенств на $ (-1) $) можно переписать в виде $$ G_1(alpha,beta,dots) > 0, dots, G_n(alpha,beta,dots) > 0 . $$ Здесь $ G_1,dots, G_n $ — полиномы от $ alpha,beta,dots $. Если при некотором наборе значений $ alpha=alpha_0, beta=beta_0, dots $ эта система удовлетворена, при непрерывной вариации этих параметров $ alpha_0+delta_, beta_0 + delta_,dots $ какое из неравенств системы нарушится в первую очередь, т.е. раньше остальных? Иными словами: какое из неравенств системы самое важное? — Оказывается, последнее.

Теорема[2]. Пусть $ f_ <<coloralpha >>(x_1,dots,x_n) $ — квадратичная форма, зависящая от параметра $ <coloralpha > $ линейным образом:

Справедливо и более общее утверждение.

Теорема[1,5]. Если при непрерывном изменении коэффициентов формы $ f_ $ ее ранг $ _ $ остается неизменным, то не изменяется и ее сигнатура $ sigma_(f) $.

В случае, когда главные миноры матрицы $ mathbf A $ обращаются в нуль, к анализу канонического вида квадратичной формы приходится привлекать «тяжелую артиллерию» в виде ведущих миноров. Но, по крайней мере, один теоретический результат можно сформулировать немедленно.

Теорема. В произвольной квадратичной форме $ f(X) $ ранга $ mathfrak rge 1 $ можно так перенумеровать переменные, чтобы в матрице получившейся квадратичной формы $ tilde f(Y) $ в последовательности главных миноров

$$ det widetilde_1, dots, det widetilde_ $$ не было двух подряд идущих нулевых и $ det widetilde_ ne 0 $.

Конгруэнтность квадратичных форм

Матрицы $ $ и $ $, связанные соотношением $ =C^C $ при некоторой неособенной матрице $ C $, называются конгруэнтными: $ cong $. Если, вдобавок, матрицы $ $ и $ $ симметричны, то конгруэнтными называются и соответствующие им квадратичные формы $ X^X $ и $ X^X $.

Теорема. Квадратичные формы $ X^X $ и $ X^X $ конгруэнтны тогда и только тогда, когда совпадают их индексы инерции, или, что то же, равны их ранги и сигнатуры.

Из всего разнообразия канонических видов квадратичной формы выберем самый простой, именно тот, коэффициенты которого равны $ +1 $ или $ (-1) $. Например, если квадратичная форма $ f(X) $ уже приведена к каноническому виду $$widetilde f(Y)=alpha_1y_1^2+dots+alpha_ y_^2 .$$ то преобразование $$y_j=frac<sqrt> npu jin <1,dots, > , y_j=z_j npu jin <+1,dots, n > $$ приводит эту форму к виду $$ z_1^2+dots + z_<n_(A)>^2 -z_<n_(A)+1>^2 — dots — z_<>^2 , $$ который называется нормальным видом квадратичной формы.

Множество всех квадратичных форм с вещественными коэффициентами можно разбить на классы эквивалентности, в каждом из которых будут находиться только конгруэнтные между собой формы. Каждый из классов полностью описывается каким-то из своих представителей. Таким представителем можно взять нормальный вид.

Какое преобразование квадратичной формы оставляет ее инвариантной?

Теорема [Эрмит]. Квадратичная форма $ X^X $ переходит в себя при преобразовании

Видео:Как решить любую задачу студенту? : Интеллектуальный поисковик wolframalpha.comСкачать

Знакоопределенность

Квадратичная форма $ f_(X) $ называется

а) неотрицательной если $ f(X)ge 0 $ для любого $ Xin mathbb R^n $;

б) положительно определенной, если она неотрицательна и $ f(X)= 0 $ только при $ X=mathbb O_ $;

в) неопределенной или знакопеременной, если существуют $ subset mathbb R^n $ такие что числа $ f(X_1) $ и $ f(X_2) $ имеют разные знаки: $ f(X_1)f(X_2) глобальным. В случае положительной определенности точка $ X=mathbb O $ будет единственной точкой пространства $ mathbb R^ $, в которой $ f_(X) $ достигает своего минимального значения. Однако если свойство положительной определенности будет нарушено: $ f(X_1) =0 $ при $ X_1 ne mathbb O $, то вследствие однородности формы $ f_(X) $ будет выполнено $$ f(tX_1)=t^2f(X_1)= 0 quad npu quad forall t in mathbb R . $$ Иными словами, свое минимальное значение $ 0_ $ неотрицательная, но не положительно определенная, форма $ f_ (X) $ будет принимать на всей прямой, проходящей через точки $ mathbb O $ и $ mathbb X_1 $. Точка $ X=mathbb O $ перестает быть изолированной точкой минимума: в любой ее окрестности находятся другие точки минимума. С точки зрения здравого смысла, подобная ситуация может считаться исключительным, вырожденным случаем. Интуиция подтверждается аналитикой: как увидим впоследствии вероятность того, что случайным образом выбранная квадратичная форма, обладающая свойством неотрицательности, не будет, вдобавок, положительно определенной, равна $ 0_ $. Событие теоретически возможно, но практически немыслимо.

Оказывается условие положительной определенности формы $ f $ является необходимым и достаточным для обеспечения подобного свойства в произвольном пространстве $ mathbb R^n $. И это утверждение верно не только для квадратичной формы, но и для однородного полинома (формы) произвольного порядка.

Задача об условных экстремумах квадратичной формы $ f_(X) $ на сфере $ x_1^2+dots+x_n^2 =1 $ решается ☞ ЗДЕСЬ.

Пример. В произвольном евклидовом пространстве $ mathbb E $ квадратичная форма с матрицей Грама произвольной системы векторов $ subset mathbb E $

Задача. Найти условия неотрицательности и положительной определенности квадратичной формы в терминах ее коэффициентов.

Очевидны необходимые условия неотрицательности квадратичной формы $$ f(X)=displaystyle sum_ f_x_jx_k : $$ все коэффициенты при квадратах переменных должны быть неотрицательными: $$ f_ge 0, dots , f_ge 0 . $$ Также очевидно, что эти условия будут и достаточными, если все остальные коэффициенты $ f_^ $ при $ jne k $ равны нулю. Если же последнее условие не выполняется, то имеет смысл предварительно преобразовать квадратичную форму к сумме квадратов, т.е. исследовать ее канонический вид.

Теорема. Ненулевая квадратичная форма, представленная в правильном виде

$$ f(X)=X^X , , $$ будет неотрицательной тогда и только тогда, когда ее отрицательный индекс инерции равен нулю: $$ n_ ()=0 qquad iff qquad qquad sigma ( )=operatorname .$$ Если это условие выполнено, то для положительной определенности формы необходимо и достаточно чтобы она была невырождена: $ det ne 0 $.

Доказательство ☞ ЗДЕСЬ.

К счастью, явное представление канонического вида квадратичной формы уже имеется — как правило, он задается формулой Якоби. Индексы инерции вычисляются через знаки главных миноров матрицы квадратичной формы.

Теорема [Сильвестр]. Квадратичная форма

$$ f(X)=X^X $$ будет положительно определенной тогда и только тогда, когда все главные миноры ее матрицы положительны: $$ a_>0, left| begin a_ & a_ \ a_ & a_ end right| >0, left| begin a_ & a_ & a_ \ a_ & a_ & a_ \ a_ & a_ & a_ end right| >0, dots, det >0 . $$

Доказательство ☞ ЗДЕСЬ.

Квадратичная форма будет отрицательно определенной тогда и только тогда, когда знаки главных миноров ее матрицы будут чередоваться следующим образом:

Пример. Найти все значения параметра $ <coloralpha > $, при которых квадратичная форма

$$2, x_1^2+2, x_2^2+x_3^2+ 2, <color > , x_1x_2+6, x_1x_3 +2,x_2x_3 $$ будет положительно определенной.

Решение. Значения главных миноров: $$det _1=2, det _2=4- <coloralpha >^2, det _3=- <coloralpha >^2+ 6, <coloralpha > -16 . $$ Последнее выражение будет отрицательно при любых $ <coloralpha > in mathbb R $.

Ответ. Таких значений нет: $ <coloralpha > in varnothing $.

Можно ли получить условия неотрицательности квадратичной формы: $$ f(X) ge 0 npu forall X in ^n $$ превращением всех неравенств из критерия Сильвестра в нестрогие: $ > to <color > ge $ ? — Вообще говоря, нет.

Пример. Квадратичная форма

$$f(x_1,x_2,x_3,x_4)=x_1^2+2x_1x_3+2x_2x_4+x_4^2= X^ left( begin 1&0&1 &0 \ 0&0&0&1 \ 1&0&0&0 \ 0&1&0&1 end right)X $$ — неопределенная, т.к. $ f(1,0,-1,0)=-1_ 0 $. Тем не менее, все главные миноры ее матрицы неотрицательны. ♦

Имеются ли конструктивные необходимые и достаточные условия неотрицательности квадратичной формы?

Теорема. Для неотрицательности квадратичной формы $ X^ mathbf A X $ необходимо и достаточно, чтобы все ведущие миноры матрицы $ mathbf A $, т.е. миноры, стоящие на пересечении строк и столбцов матрицы с одинаковыми номерами

$$ Aleft( begin j_1 & dots & j_k \ j_1 & dots & j_k end right) , j_1 0 $ при всех $ Xin mathbb V_1, X ne mathbb O $.

Теорема. Пусть линейное подпространство задано системой линейных однородных уравнений

$$ left< begin h_x_1 & + dots & + h_x_n&=0, \ dots & & & dots \ h_x_1 & + dots & + h_x_n&=0, \ end right. qquad iff qquad underbrace<left( begin h_ & dots & h_ \ dots & & dots \ h_ & dots & h_ end right)>_X=mathbb O $$ Здесь $ k ☞ ЗДЕСЬ.

Пример. Найти ортогональную замену переменных, приводящую квадратичную форму

$$ X^ mathbf A X quad npu quad =left(begin 2 & 2 & -1 \ 2 & -1 & 2 \ -1& 2 & 2 end right) $$ к каноническому виду.

Решение. Характеристический полином $ det (mathbf A- lambda E)=-(lambda-3)^2(lambda+3) $. Простому собственному числу $ lambda=-3 $ соответствует собственный вектор $ _1=[1,-2,1]^<^> $, а собственному числу $ lambda=3 $ второй кратности соответствуют два линейно-независимых собственных вектора $ _2=[2,1,0]^<^> $ и $ _3=[-1,0,1]^<^> $. Очевидно, что $ langle _1, _2rangle=0 , langle _1, _3 rangle =0 $, но $ langle _2, _3 rangle ne 0 $. Ортогонализуем систему векторов $ left<_2,_3right> $: $$_2=_2, _3=_3+ <coloralpha > _2 quad mbox langle _2,_3rangle =0 Longrightarrow <coloralpha >=-frac<langle _2,_3rangle> <langle _2,_2rangle>=frac $$ и $ _3=left[-1/5, 2/5, 1 right]^<^> $. После нормирования, получаем ортогональную матрицу $$ P=left(begin 1/sqrt & 2/sqrt & -1/sqrt \ -2/sqrt & 1/sqrt & 2/sqrt \ 1/sqrt & 0 & 5/sqrt end right) . $$ Замена переменных $ X=PY $ приводит квадратичную форму $ X^ mathbf A X $ к каноническому виду $$ (y_1,y_2,y_3) left(begin -3 & 0 & 0 \ 0 & 3 & 0 \ 0& 0 & 3 end right) left( begin y_1 \ y_2 \ y_3 end right)=-3,y_1^2+3,y_2^2+3,y_3^2 . $$

Теорема. Если известны коэффициенты характеристического полинома матрицы квадратичной формы $ f(X)=X^mathbf A X $:

$$ det (mathbf A- lambda E) equiv (-1)^n left(lambda^n+a_lambda^+ dots + a_n right) , ,$$ то $$ operatorname (f(X))= iff a_=a_=dots=a_<+1>=0,a_<>ne 0 , . $$ В этом случае будет также выполнено $$ n_ (f(X))=(1,a_1,dots,a_<>),quad n_ (f(X))=(1,a_1,dots,a_) , , $$ $$ sigma(f(X))=sum_^ operatorname (a_a_j) quad npu quad a_0=1 , . $$

Доказательство основано на правиле знаков Декарта.

Видео:Видеоурок "Приведение к каноническому виду"Скачать

Геометрия замен переменных

В предыдущих пунктах мы рассмотрели два подхода к построению канонического вида квадратичной формы. Очевидно, что подход, основанный на ортогональной замене переменных более дорогостоящий в построении по сравнению с методом Лагранжа. В самом деле, он требует нахождения собственных чисел симметричной матрицы, т.е. решения алгебраического уравнения $ det (mathbf A — lambda E)=0 $. В случае матриц порядка $ n> 4 $ корни этого уравнения, как правило, на находятся в виде «хорошей» комбинации коэффициентов, и могут быть определены разве лишь приближенно. Метод же Лагранжа принципиально безошибочен: коэффициенты канонического вида определяются в виде рациональных функций от коэффициентов квадратичной формы.

Пример. Уравнение $ 1/3x_1^2-x_1x_2+x_2^2=1 $ задает на плоскости эллипс:

Преобразование $$ y_1=x_1-3/2x_2, y_2=x_2 $$ приводит уравнение к виду $$ 1/3 y_1^2+1/4 y_2^2=1 ; $$ в новых координатах кривая имеет вид на рисунке слева. С другой стороны, преобразование $$ begin z_1&= sqrt<1/2+1/sqrt>,x_1+sqrt<1/2-1/sqrt>,x_2,\ z_2&= sqrt<-1/2-1/sqrt>,x_1+sqrt<1/2+1/sqrt>x_2 end $$ приводит уравнение к виду $$frac<4-sqrt>z_1^2+frac<4+sqrt>z_2^2=1 . $$ В этих координатах кривая имеет вид на рисунке справа.

Оба преобразования координат не изменяют типа кривой: эллипс остается эллипсом. Но второе преобразование дает нечто большее: оно сохраняет размеры. Фактически, оно сводится к повороту исходного эллипса.

Вывод. Метод Лагранжа «дешевле» метода ортогональных преобразований при решении задачи классификации алгебраических многообразий, заданных уравнением вида $ X^ mathbf A X=1 $. Иными словами, он позволяет «дешевле» определить тип поверхности с точностью до ее формы: например, в $ mathbb R^3 $ является ли эта поверхность эллипсоидом или гиперболоидом (и каким именно — однополостным или двуполостным)? Но если нас интересуют истинные размеры этой поверхности: например, размеры посылочного ящика, в который эллипсоид, заданный уравнением $ X^ mathbf A X=1 $, можно было бы поместить — то здесь без собственных векторов и чисел матрицы $ mathbf A $ не обойтись!

Видео:Приводим уравнение кривой 2 порядка к каноническому видуСкачать

WolframAlpha по-русски

Математика с WolframAlpha ® . Объяснения с примерами.

Приведение матрицы к ступенчатому виду: пошаговое решение в Wolfram|Alpha

Приведение матрицы к ступенчатому виду — промежуточный этап при решении систем линейных алгебраических уравнений, нахождения обратной матрицы, других задач линейной алгебры. Приведение матрицы к ступенчатому виду также называют преобразованием Гаусса-Жордана.

Для приведения матрицы к ступенчатому виду «вручную» к строкам матрицы применяются элементарные преобразования: строки матрицы можно менять местами, умножать или делить на ненулевое число, складывать и вычитать. В Wolfram|Alpha для приведения матрицы к ступенчатому виду служит запрос row reduce, например:

Чтобы получить пошаговое решение Вы должны заранее зарегистрироваться в Wolfram|Alpha и войти в свой аккаунт.

Полученное решение можно рассматривать пошагово, нажимая последовательно кнопку «Next step» («Следующий шаг»):

Нажав кнопку «Show all steps» («Показать все шаги») сразу получим полное решение:

Для квадратной невырожденной матрицы в результате приведения матрицы к ступенчатому виду получим диагональную матрицу с единицами по главной диагонали:

Помните, для получения пошагового решения Вам нужно войти в свой аккаунт в Wolfram|Alpha. Обратите внимание: Wolfram|Alpha предупреждает Вас, что пользователь бесплатного аккаунта может получить не более 3-х пошаговых решений в течение суток.

Вот, как выглядит полное решение в этом случае:

Видео:Приведение линейного уравнения в частных производных c постоянными коэфф--ми к каноническому виду.Скачать

Приведение к каноническому виду линейных уравнений с частными производными второго порядка

Федеральное агентство по образованию

ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Институт математики, экономики и информатики

Кафедра дифференциальных и интегральных уравнений

ПРИВЕДЕНИЕ К КАНОНИЧЕСКОМУ ВИДУ ЛИНЕЙНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ВТОРОГО ПОРЯДКА

Приведение к каноническому виду линейных уравнений с частными производными 2-го порядка с двумя независимыми переменными …………………………………………………………………………

1.1. Необходимый теоретический материал………………………..

1.2. Пример выполнения задачи1 (приведение к

каноническому виду уравнений гиперболического типа) .

1.3. Пример выполнения задачи 2 (приведение к

каноническому виду уравнений параболического типа)

1.4. Пример выполнения задачи 3 (приведение к

каноническому виду уравнений эллиптического типа) ..

1.5. Задачи для самостоятельного решения ………………….….

Упрощение группы младших производных

для уравнений второго порядка с постоянными коэффициентами

2.1. Необходимый теоретический материал …………………..

2.2. Пример выполнения задачи 4

2.3. Задачи для самостоятельного решения ……………………..

В настоящих методических указаниях изложен теоретический материал и на конкретных примерах разобрано приведение к каноническому виду линейных уравнений с частными производными второго порядка с двумя независимыми переменными для уравнений гиперболического, эллиптического и параболического типов.

Методические указания предназначены для студентов математических специальностей очной и заочной формы обучения.

§1. Приведение к каноническому виду линейных уравнений с частными производными 2-го порядка с двумя независимыми переменными.

Задача. Определить тип уравнения

(1)

и привести его к каноническому виду.

1.1. Необходимый теоретический материал.

I. Тип уравнения (1) определяется знаком выражения :

· если в некоторой точке, то уравнение (1) называется уравнением гиперболического типа в этой точке;

· если в некоторой точке, то уравнение (1) называется уравнением эллиптического типа в этой точке;

· если в некоторой точке, то уравнение (1) называется уравнением параболического типа в этой точке.

Уравнение (1) будет являться уравнением гиперболического, эллиптического, параболического типа в области D, если оно гиперболично, эллиптично, параболично в каждой точке этой области.

Уравнение (1) может менять свой тип при переходе из одной точки (области) в другую. Например, уравнение является уравнением эллиптического типа в точках ; параболического типа в точках ; и гиперболического типа в точках .

II. Чтобы привести уравнение к канонического виду, необходимо:

1. Определить коэффициенты ;

2. Вычислить выражение ;

3. Сделать вывод о типе уравнения (1) (в зависимости от знака выражения );

4. Записать уравнение характеристик:

; (2)

5. Решить уравнение (2). Для этого:

а) разрешить уравнение (2) как квадратное уравнение относительно dy:

; (3)

б) найти общие интегралы уравнений (3) (характеристики уравнения (1)):

· (4)

в случае уравнения гиперболического типа;

· , (5)

в случае уравнения параболического типа;

· , (6)

в случае уравнения эллиптического типа.

6. Ввести новые (характеристические) переменные и :

· в случае уравнения гиперболического типа в качестве и берут общие интегралы (4) уравнений (3), т. е.

· в случае уравнения параболического типа в качестве берут общий интеграл (5) уравнения (3), т. е. , в качестве берут произвольную, дважды дифференцируемую функцию , не выражающуюся через , т. е. ;

· в случае уравнения эллиптического типа в качестве и берут вещественную и мнимую часть любого из общих интегралов (6) уравнений (3):

7. Пересчитать все производные, входящие в уравнение (1), используя правило дифференцирования сложной функции:

, (7)

8. Подставить найденные производные в исходное уравнение (1) и привести подобные слагаемые. В результате уравнение (1) примет один из следующих видов:

· в случае уравнения гиперболического типа:

;

· в случае уравнения параболического типа:

;

· в случае уравнения эллиптического типа:

1.2. Пример выполнения задачи 1.

Определить тип уравнения

и привести его к каноническому виду.

1. Определим коэффициенты :

2. Вычислим выражение :

3. уравнение гиперболического типа во всей плоскости XOY.

4. Запишем уравнение характеристик:

. (9)

5. Решим уравнение (9). Для этого:

а) разрешаем уравнение (9) как квадратное уравнение относительно dy: ;

;

(10)

б) найдём общие интегралы уравнений (10) (характеристики уравнения (9)):

6. Введём характеристические переменные:

7. Пересчитаем производные, входящие в исходное уравнение.

Используя формулы (7), получим:

Здесь слева написаны коэффициенты уравнения (8) при соответствующих производных.

8. Собирая подобные слагаемые, получим:

Или после деления на -100 (коэффициент при ):

Ответ. Уравнение (8) является уравнением гиперболического типа на всей плоскости XOY. Канонический вид

где

1.3. Пример выполнения задачи 2.

Определить тип уравнения

и привести его к каноническому виду.

1. Определим коэффициенты . В нашем примере они постоянны:

2. Вычислим выражение :

3. уравнение параболического типа во всей плоскости XOY.

4. Запишем уравнение характеристик:

. (12)

5. Решим уравнение (12). Для этого:

а) разрешаем уравнение (9) как квадратное уравнение относительно dy. Однако в этом случае левая часть уравнения является полным квадратом:

;

(13)

б) имеем только одно уравнение характеристик (13). Найдём его общий интеграл (уравнения параболического типа имеют только одно семейство вещественных характеристик):

6. Введём характеристические переменные: одну из переменных вводим как и ранее

а в качестве берут произвольную, дважды дифференцируемую функцию, не выражающуюся через , пусть

;

7. Пересчитаем производные, входящие в исходное уравнение.

Используя формулы (7), получим:

Здесь слева написаны коэффициенты уравнения (11) при соответствующих производных.

8. Собирая подобные слагаемые, получим:

Функцию, стоящую в правой части уравнения (11) необходимо также выразить через характеристические переменные.

После деления на 25 (коэффициент при ):

Ответ. Уравнение (11) является уравнением параболического типа на всей плоскости XOY. Канонический вид

где

1.4. Пример выполнения задачи 3.

Определить тип уравнения

(14)

и привести его к каноническому виду.

1. Определим коэффициенты :

2. Вычислим выражение :

3. уравнение эллиптического типа во всей плоскости XOY.

4. Запишем уравнение характеристик:

. (15)

5. Решим уравнение (15). Для этого:

а) разрешаем уравнение (15) как квадратное уравнение относительно dy: ; (16)

б) уравнения (16) – это пара комплексно-сопряженных уравнений. Они имеют пару комплексно-сопряженных общих интегралов. (Уравнения эллиптического типа не имеют вещественных характеристик)

(17)

6. Введём характеристические переменные как вещественную и мнимую части одного из общих интегралов (17):

7. Пересчитаем производные, входящие в исходное уравнение.

Используя формулы (7), получим:

Здесь слева написаны коэффициенты уравнения (14) при соответствующих производных.

8. Собирая подобные слагаемые, получим:

Или после деления на 4 (коэффициент при и ):

Ответ. Уравнение (14) является уравнением эллиптического типа на всей плоскости XOY. Канонический вид

где

1.5. Задачи для самостоятельного решения.

Определить тип уравнения и привести его к каноническому виду.

§2. Упрощение группы младших производных

для уравнений второго порядка с постоянными коэффициентами

2. 1. Необходимый теоретический материал

В самом общем виде линейное уравнение с частными производными второго порядка с двумя независимыми переменными имеет вид

(1)

Преобразованием независимых переменных группа старших производных уравнения может быть упрощена. Уравнение (1) приводится к одному из следующих видов

· в случае уравнения гиперболического типа:

; (11)

· в случае уравнения параболического типа:

; (12)

· в случае уравнения эллиптического типа:

. (13)

Если коэффициенты исходного уравнения постоянны, то для дальнейшего упрощения уравнения любого типа нужно сделать замену неизвестной функции

, (14)

где — новая неизвестная функция, — параметры, подлежащие определению. Такая замена не «испортит» канонического вида, но при этом позволит подобрать параметры так, чтобы из трех слагаемых группы младших производных в уравнении осталось только одно. Уравнения гиперболического, параболического и эллиптического типов соответственно примут вид

;

Чтобы реализовать замену (14) в уравнениях (11), (12), (13), необходимо пересчитать все производные, входящие в эти уравнения по формулам

(15)

Подробно рассмотрим этот процесс на примере уравнения гиперболического типа, т. е. уравнения (11). Пересчитаем производные, входящие в это уравнение, используя формулы (15).