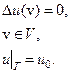Уравнению Лапласа удовлетворяет не только потенциал гравитационного поля вне области содержащий источники, но и все его производные вместе с их линейными комбинациями. Этому уравнению в свободном пространстве, т.е. в области, где отсутствуют источники, удовлетворяют и многие другие геофизические поля – компоненты напряженности магнитного поля, естественного электрического, теплового для установившегося температурного режима поля при постоянных электропроводности и теплопроводности среды. Уравнение Лапласа это фундаментальное внеметодное уравнение в геофизике, а функции ему удовлетворяющие называются гармоническими.
Задачей Дирихледля уравнения Лапласа называется задача нахождения значений гармонической функции внутри области по ее граничным – краевым значениям на границе области. Ее также называют задачей аналитического продолжения потенциального поля. Это устоявшееся, но не совсем удачное название. Формально краевая задача Дирихле записывается следующим образом:
Г – граница области V.
На самом деле для однозначности ее решения необходимо добавление еще дополнительных условий. Однако в некоторых частных случаях достаточно простейших из них.
Частным случаем этой задачи является задача Дирихле для полупространства. Формулируется она следующим образом. Пусть плоскость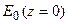 
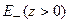
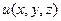
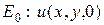
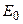
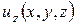
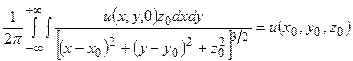, разбивает все пространство на нижнее 
, в котором сконцентрированы все источники поля, и верхнее 
, в котором источники заведомо отсутствуют. Гармоническая в области 
функция 
задана своими краевыми значениями на 
. Считаем, что 
непрерывна на 
и стремится к нулю на бесконечности. Тогда значения 
в любой точке области находится по с помощью известного интеграла Пуассона, дающего решение задачи Дирихле для полупространства:
 | (2.6) |
В двухмерном случае интеграл Пуассона имеет вид:
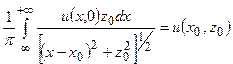 | (2.6а) |
Каждое из приведенных соотношений может быть также как и ранее, записано в операторной форме:
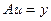 . | (2.7) |
Расчет интеграла Пуассона, как для двухмерного, так и для трехмерного случаев является типичной задачей из области решения уравнений математической физики. Она не содержит «подводных камней». Она имеет решение, это решение единственно и устойчиво зависит от начальных данных во всех имеющих смысл нормах. Степень гладкости продолженного поля, т.е.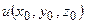 
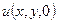
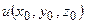
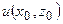
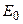
для (6) всегда выше, чем степень гладкости краевых значений 
. Мы пока обращаемся к интуитивному пониманию смысла гладкости. Однако, эта задача может рассматриваться и как обратная задача – нахождения по известному или 
на некотором множестве в значения этих функций на . В операторной постановке (7) это соответствует расчету величины u под знаком оператора A по заданной правой части y. При попытке решения этой обратной задачи возникает целый «букет» неприятностей, которые почти очевидны. Они начинаются с того, что совсем не факт, что решение будет существовать для конкретных данных. И уже совершенно очевиден факт, что гладкость результата будет ниже, и даже катастрофически ниже гладкости исходных данных. Решение будет неустойчиво, разваливаться от малейших вариаций исходных данных. Это проявление тех же эффектов, предупреждение о которых было сделано выше
Задача Дирихле в круге. Интеграл Пуассона
Видео:Уравнения математической физики 15+16 Задача Дирихле для уравнения Лапласа - Пуассона в кругеСкачать
и граничному условию
где окружность Сго — граница круга Kro, a f — заданная на ней непрерывно дифференцируемая функция.
Запишем уравнение (8.1) в полярных координатах:
1 д / ди 1 д 2 г
Будем искать частные решения этого уравнения в виде и(т, r
Заметим, что u(r, 2 . Если А = 0, то из (8.5) следует
— (г—— )=0, R(r) = ед In г + С2, (8.7)
Видео:6.2 Решение задач для уравнения Лапласа в круге, вне круга и в кольцеСкачать
где с и С2 — постоянные. Поскольку и(г, р) непрерывна в замкнутом круге и, следовательно, ограничена, a In г —> оо при г 0, то с.[ = 0. При А = п 2 0 решение уравнения (8.5) ищем в виде R — r k , см. [1] или [28]. Подставляя эту функцию в уравнение и сокращая на r k , найдем к 2 = п 2 , или к = ±п (п > 0) и, следовательно, R(r) = сг
п + С2Г П , где с и — постоянные. Опять следует положить с = 0, так как R(r) непрерывна внутри круга. Итак, найдены частные решения
Замечание. Гармоническая функция ип(г,р) являетея однородным многочленом степени п относительно декартовых координат х, у, так как согласно формуле Муавра
r n (cos р + г sin р) п = r n (cos пр + г sin пр),
т. е. r n cos пр = Re(o? + iy) n , r n sin p = Im(a? + iy) n (здесь i 2 = -l, [17]).
Полиномы вида Pn(x,y) = a„Re(x + iy) n + 67)Im(x + iy) n называются однородными гармоническими многочленами.
Решение задачи (8.1)-(8.2) будем искать в виде
Видео:Задача Дирихле для круга. Уравнение ЛапласаСкачать
4 Э. Р. Розендорн, Е.С. Соболева, Г. М. Фатеева
Для определения коэффициентов ап и Ьп воспользуемся условием (8.2):
считая, что f задана как функция угла р. Тогда из разложения /( 27Г
При предположениях, сделанных относительно функции /( г/vq 2 Г f 1 +°° / г п )
= — /(V9 й + У? ( — ) ( cos n V ; cos n
1 2 / Г 1 +°° 7 Г П 1
= — /ОЖ й + 12 ( — ) С08? Ф -V0 (8.И)
Видео:OTAROVA JAMILA МЕТОД ФУРЬЕ РЕШЕНИЯ ЗАДАЧИ ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕСкачать
Используя следствие из формулы Эйлера: cos а = ^(е г(Х + е га ), и формулу суммы бесконечно убывающей геометрической прогрессии: 52 с 1 п =
, |q| n cos па = | | ? t n (e““ + е — ““) =
to 1 1 -1 2
2 ‘ 1 — te ta 1 — te
ta / 2 1 — 21 cos a +t 2
Подставляя (8.12) при t = r/r^, а = г ф в (8.11), получим
Ж) 2 9 0 .—- 8 — 13 >
J г 2 — 2гог cos( Tq
Видео:Решение уравнения Лапласа в шареСкачать
Полученная формула (8.13), дающая решение задачи Дирихле в круге А’го, носит название интеграла Пуассона.
Замечание 1. Положим в (8.13) г = 0. Тогда будем иметь
т. е. значение гармонической функции в центре круга равно ее среднему значению на окружности.
Замечание 2. Как следует из формул (8.8)—(8.10) и (8.13), внутри круга г vq гармоническая функция является аналитической функцией.
Замечание 3. Аналогично можно рассмотреть решение внешней задачи Дирихле для круга, т. е. найти непрерывную вне круга Кго и на его границе функцию и, удовлетворяющую уравнению (8.1) вне этого круга, ограниченную на бесконечности и удовлетворяющую условию (8.2) на границе круга. Функции Ф( ) определяются теми же формулами, что и выше, a R = сг
п при п > 0, либо 7?.(г) = С2 при п = 0. Поэтому вместо (8.8) решение будет определяться формулой
где постоянные ап, Ъп являются в силу (8.9) коэффициентами Фурье функции /( Г 0
Видео:6.1 Уравнение Лапласа в полярных координатах. Принцип решения и постановка задачСкачать
Z7T J — ZrrQ COS( Zq
🎦 Видео
Уравнение Лапласа. Задача Дирихле для уравнения Лапласа внутри и вне кругаСкачать
Задача Дирихле для шараСкачать
7.2 Уравнение Лапласа в секторе и кольцевом сектореСкачать
Лекция №5 по УМФ. Задача Дирихле для ур-ия Лапласа в круге. Константинов Р. В.Скачать
7.1 Решение уравнения Лапласа в прямоугольникеСкачать
Задача Дирихле для уравнения Лапласа в кольце и сектореСкачать
Методы математической физики. Задача Дирихле для уравнения Лапласа в круге. 19.05.21 Фролова Е.В.Скачать
Уравнение Пуассона и задача ДирихлеСкачать
Теория функций комплексного переменного 21. Решение общей задачи ДирихлеСкачать
Попов И.Ю. Функция Грина задачи Дирихле для уравнения ЛапласаСкачать
Горицкий А. Ю. - Уравнения математической физики. Часть 2 - Функция ГринаСкачать
Задача Дирихле и НейманаСкачать
9. Уравнение ПуассонаСкачать
