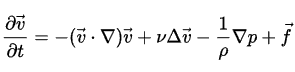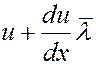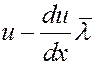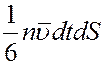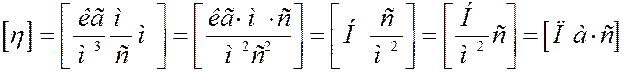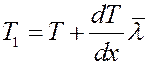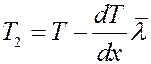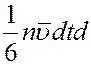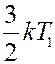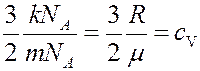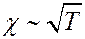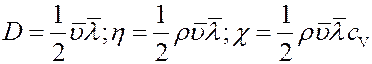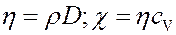Внутреннее трение в газах уравнение ньютона (7 видео)

Основные законы движения жидкостей и газов

Для расчета движения воды в трубопроводе нужно знать не так уж и много. Для этого не надо глубоко изучать физику, но всё же некоторое основные понятия изучить придется.

В этой статье я приведу самые основные формулы, которые вам пригодятся не только для расчетов, но и для общего понимания, что может влиять в вашем водопроводе на его течение. Иногда общее понимание процессов поможет вам избежать ошибок при монтаже системы.

Например, не все знают, что в части водопровода с трубами меньшего диаметра давление на стенки меньше, чем на участке с трубами большего диаметра. Почему возникает кавитация и вообще, что это такое. А это надо знать.

Статья будет обновляться и дополняться.

Содержание

Уравнение неразрывности
Уравнение Бернулли стационарного движения
Явление кавитации
Гидродинамика Эйлера и Навье-Стокса
Закон вязкого трения Ньютона
Уравнение Навье — Стокса для вязких жидкостей
Критерий Рейнольдса
Внутреннее трение (вязкость газов). Теплопроводность газов.
Вязкость (внутреннее трение). Закон Ньютона. Коэффициент вязкости
🎦 Видео

Видео:Урок 40 (осн). Трение качения. Трение в жидкостях и газахСкачать

Уравнение неразрывности

Для жидкости, текущей в трубе, этот закон используют в такой форме (называемой уравнением неразрывности):

Где v — скорость жидкости S — площадь сечения трубы, по которой течёт жидкость. Сформулировать этот закон можно и так:

Сколько вливается жидкости в ёмкость, в данном случае в трубу, столько должно и выливаться, если условия течения не изменяются.

Скорость в узких участках трубы должна быть выше, чем в широких.

Видео:Внутреннее трение в газахСкачать

Уравнение Бернулли стационарного движения

Одно из важнейших уравнений гидромеханики было получено в 1738 г. швейцарским учёным Даниилом Бернулли (1700 — 1782). Ему впервые удалось описать движение идеальной жидкости, выраженной в формуле Бернулли.

Идеальная жидкость — жидкость, в которой отсутствуют силы трения между элементами идеальной жидкости, а также между идеальной жидкостью и стенками сосуда.

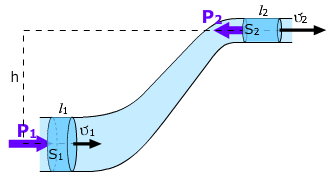
Уравнение стационарного движения, носящее его имя, имеет вид:

P +	ρ⋅v²	+ ρ⋅g⋅h = const
	2

где P — давление жидкости, ρ − её плотность, v — скорость движения, g — ускорение свободного падения, h — высота, на которой находится элемент жидкости.

Смысл уравнения Бернулли в том, что внутри системы заполненной жидкостью (участка трубопровода) общая энергия каждой точками всегда неизменна.

В уравнении Бернулли есть три слагаемых:

ρ⋅v 2 /2 — динамическое давление — кинетическая энергия единицы объёма движущей жидкости;
ρ⋅g⋅h — весовое давление — потенциальная энергия единицы объёма жидкости;
P — статическое давление, по своему происхождению является работой сил давления и не представляет собой запаса какого-либо специального вида энергии («энергии давления»).

Это уравнение объясняет почему в узких участках трубы растёт скорость потока и падает давление на стенки трубы. Максимальное давление в трубах устанавливается именно в месте, где труба имеет наибольшее сечение. Узкие части трубы в этом отношении безопасны, но в них давление может упасть настолько, что жидкость закипит, что может привести к кавитации и разрушению материала трубы.

Видео:Вязкость. Ламинарное и турбулентное течения жидкостей. 10 класс.Скачать

Явление кавитации

Кавитация (от латинского cavitas — «углубление», «полость») — процесс образования полостей (пузырьков) в движущейся жидкости вследствие понижения давления.

Явление кавитации также объясняется уравнением Бернулли. Если скорость течения жидкости значительно возрастает, то давление сильно понизится — настолько, что жидкость закипит. Такую скорость можно получить, если пропускать жидкость через очень узкий участок трубы или при быстром обращении лопатки в водяном насосе.

Пузырьки по ходу движения жидкости попадают в области жидкости с нормальным давлением и там схлопываются. Это схлопывание сопровождается гидродинамическими эффектами, способными привести к разрушению трубы или стенок насоса.

Видео:Трение в газах, внутреннее трениеСкачать

Гидродинамика Эйлера и Навье-Стокса

Уравнение Бернулли позволяет объяснить очень много интересных гидродинамических явлений, но гораздо больше явлений, происходящих в движущихся жидкостях и газах, с его помощью объяснить нельзя, потому что этот закон для идеальной жидкости, т.е для жидкости, которая не обладает внутренним трением, а значит не создает гидравлическое сопротивление..

Реальная жидкость отличается от идеальной и обладает внутренним трением, или по другому называют вязкостью. Два соприкасающиеся элемента жидкости, двигающиеся в одном и том же направлении, но с разными скоростями, воздействуют друг на друга. Сила взаимодействия ускоряет медленно движущийся элемент жидкости и замедляет более быстрый.

Видео:Внутреннее трение в газахСкачать

Закон вязкого трения Ньютона

Ньютон предположил, что величина этой силы (называемой силой внутреннего трения) пропорциональна разности скоростей элементов жидкости. Следовательно, сила внутреннего трения F пропорциональна изменению скорости жидкости v в направлении, перпендикулярном движению, и зависит от площади S соприкосновения элементов жидкости:

F =	η⋅S⋅	dv
		dy

η − коэффициент динамической вязкости.

Жидкости, в которых внутреннее трение подобным образом зависит от изменения скорости, называются ньютоновскими, или жидкостями с линейной вязкостью.

Величину коэффициента динамической вязкости (и справедливость данного закона) Ньютон определил с помощью несложного опыта: он передвигал по поверхности жидкости пластинку с той или иной скоростью. Для того чтобы поддерживать эту скорость постоянной, требовалась сила, которая при небольшой глубине жидкости оказалась прямо пропорциональна площади S и скорости пластинки v и обратно пропорциональна глубине жидкости h:

F =	η⋅S⋅v
	h

И хотя при увеличении глубины жидкости h сила вязкого трения пластинки не становится исчезающе малой, эта формула довольно точно описывает взаимодействие между соприкасающимися элементами жидкости.

Чем больше разность скоростей, тем больше сила, с которой они воздействуют друг на друга, заставляя притормаживать слишком быстро движущиеся элементы и разгоняя слишком медленные.

В результате относительное движение в жидкости прекращается (но иногда это может произойти не очень скоро).

Видео:Движение тел в жидкостях и газах. Лобовое сопротивление и подъемная сила. Формула Стокса. 10 класс.Скачать

Уравнение Навье — Стокса для вязких жидкостей

В более строгой формулировке линейная зависимость вязкого трения от изменения скорости движения жидкости называется уравнением Навье — Стокса. Оно учитывает сжимаемость жидкостей и газов и, в отличие от закона Ньютона, справедливо не только вблизи поверхности твёрдого тела, но и в каждой точке жидкости (у поверхности твёрдого тела в случае несжимаемой жидкости уравнение Навье — Стокса и закон Ньютона совпадают).

Любые газы, для которых выполняется условие сплошной среды, подчиняются и уравнению Навье — Стокса, т.е. являются ньютоновскими жидкостями.

Вязкость жидкости и газа обычно существенна при относительно малых скоростях, потому иногда говорят, что гидродинамика Эйлера — это частный (предельный) случай больших скоростей гидродинамики Навье — Стокса.

При малых скоростях в соответствии с законом вязкого трения Ньютона сила сопротивления тела пропорциональна скорости. При больших скоростях, когда вязкость перестаёт играть существенную роль, сопротивление тела пропорционально квадрату скорости (что впервые обнаружил и обосновал Ньютон).

Видео:93027 Внутреннее трение в газахСкачать

Критерий Рейнольдса

Такую зависимость вывел английский физик и инженер Осборн Рейнольдс (1842 — 1912).

Критерий, который помогает ответить на вопрос, есть ли необходимость учитывать вязкость, является число Рейнольдса Re. Оно равно отношению энергии движения элемента текущей жидкости к работе сил внутреннего трения.

Рассмотрим кубический элемент жидкости с длиной ребра n. Кинетическая энергия элемента равна:

E_кин =	ρ⋅n³⋅	v²
		2

Согласно закону Ньютона, сила трения, действующая на элемент жидкости, определяется так:

F =	η⋅v⋅n²	= η⋅v⋅n
	n

Работа этой силы при перемещении элемента жидкости на расстояние n составляет

а отношение кинетической энергии элемента жидкости к работе силы трения равно

E_кин	=	ρ⋅n³⋅v²
A	=	2⋅ η⋅v⋅n²

Сокращаем и получаем:

Re =	ρ⋅n⋅v
	2η

Re — называется числом Рейнольдса.

Таким образом, Re — это безразмерная величина, которая характеризует относительную роль сил вязкости.

Например, если размеры тела, с которым соприкасаются жидкость или газ, очень малы, то даже при небольшой вязкости Re будет незначительно и силы трения играют преобладающую роль. Наоборот, если размеры тела и скорость велики, то Re >> 1 и даже большая вязкость почти не будет влиять на характер движения.

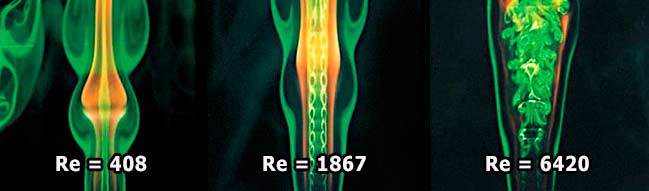
Однако не всегда большие числа Рейнольдса означают, что вязкость не играет никакой роли. Так, при достижении очень большого (несколько десятков или сотен тысяч) значения числа Re плавное ламинарное (от латинского lamina — «пластинка») течение превращается в турбулентное (от латинского turbulentus — «бурный», «беспорядочный»), сопровождающееся хаотическими, нестационарными движениями жидкости. Этот эффект можно наблюдать, если постепенно открывать водопроводный кран: тонкая струйка течёт обычно плавно, но с увеличением скорости воды плавность течения нарушается. В струе, вытекающей под большим напором, частицы жидкости перемещаются беспорядочно, колеблясь, всё движение сопровождается сильным перемешиванием.

Появление турбулентности весьма существенно увеличивает лобовое сопротивление. В трубопроводе скорость турбулентного потока меньше скорости ламинарного потока при одинаковых перепадах давления. Но не всегда турбулентность плоха. В силу того что перемешивание при турбулентности очень значительно, теплообмен — охлаждение или нагревание агрегатов — происходит существенно интенсивнее; быстрее идёт распространение химических реакций.

Формула Бернулли закон по которому течет жидкость на любом отрезке трубы, что значительно помогает при проектировании трубопроводов, особенно с естественной циркуляцией.

Все материалы, представленные на сайте, носят исключительно справочный и ознакомительный характер и не могут считаться прямой инструкцией к применению. Каждая ситуация является индивидуальной и требует своих расчетов, после которых нужно выбирать нужные технологии.

Не принимайте необдуманных решений. Имейте ввиду, что то что сработало у других, в ваших условиях может не сработать.

Администрация сайта и авторы статей не несут ответственности за любые убытки и последствия, которые могут возникнуть при использовании материалов сайта.

Сайт может содержать контент, запрещенный для просмотра лицам до 18 лет.

Видео:Урок 137. Движение тела в жидкости и газе.Скачать

Внутреннее трение (вязкость газов). Теплопроводность газов.

Вязкость газов (это же касается и жидкостей) – это свойство, благодаря которому выравниваются скорости движения разных слоев газа (жидкости). Из-за вязкости сила ветра уменьшается с течением времени, успокаиваются морские волны. Выравнивание скоростей соседних слоев газа (если они разные) происходит потому, что из слоя газа с большей скоростью переносится импульс к слою газа с меньшей скоростью. Так как этот процесс связан с переносом импульса, то газ ведет себя так, как если бы на него действовала некоторая сила – сила внутреннего трения.

Ньютон установил, что при небольших скоростях (ламинарное течение) сила внутреннего трения, действующая между слоями газа (жидкости), площадью dS определяется выражением:

(1)

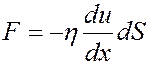
где η – коэффициент динамической вязкости, du/dx – градиент скорости в направлении оси x.

Коэффициент вязкости численно равен силе внутреннего трения, действующей на единицу площади слоя (между слоями единичной площади) при единичном градиенте скорости.

Если слои газа движутся направленно с некоторой скоростью, то на хаотическое, тепловое движение молекул со скоростью 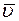накладывается направленное движение газа. Поэтому импульс каждой молекулы можно разложить на две составляющих, одна из которых обусловлена хаотическим тепловым, а вторая направленным движением молекул.

Если T = const, то составляющая импульса, обусловленная хаотическим, тепловым движением не изменяется от слоя к слою. Молекулы, которые попадают из слоя с большей скоростью направленного движения в слой с меньшей скоростью, имеют большую составляющую импульса, обусловленную направленным движением. При соударениях эти молекулы передают часть своего импульса молекулам более медленного слоя, которые увеличивают при этом скорость своего направленного движения. И наоборот молекулы более медленного слоя, попадая в более быстрый слой, при соударениях тормозят направленное движение молекул этого слоя.

Таким образом, внутреннее трение в газах обусловлено переносом импульса от слоя к слою в направлении нормали к скорости направленного движения слоев.

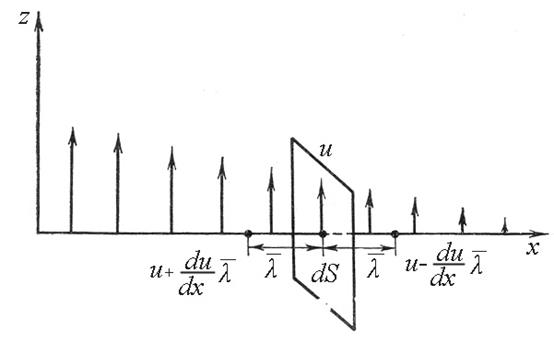
Пусть слои газа двигаются параллельно оси Z (рис.1.).

Рис.1.Перенос импульса в газах.

Градиент скорости вдоль оси x равен du/dx. Выберем площадку dS в слое со скоростью u. На расстояниях 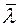от нее слева и справа скорости слоев газа будут соответственно равны:

Все направления движений молекул равновероятны из-за полной их хаотичности. Поэтому в направлении оси x движется 1/3 часть всех молекул: из них 1/6 движется слева направо и 1/6 справа налево. За время dt через площадку dS слева направо пройдет

молекул, которые перенесут через эту площадку импульс:

(2)

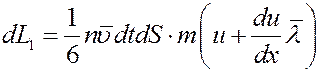
Одновременно за это же время такое же количество молекул пройдет через площадку dS справа налево, при этом они перенесут импульс:

(3)

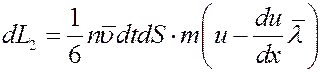
За это же время из площадки dS слоя, скорость которого равна u, вылетит такое же количество молекул и вправо и влево. Но так как скорости этих молекул одинаковые, равные u и направлены в разные стороны изменение импульса слоя при этом будет равно нулю. С учетом этого импульс, который перенесется через площадку dS в положительном направлении оси x, равен:

(4)

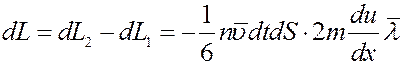
Учитывая, что mn = ρ – плотность газа, из (4) получим:

(5)

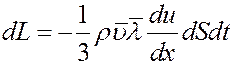
Из (5) видно, что знак минус показывает, что импульс переносится в направлении уменьшения скорости слоев.

Согласно II закону Ньютона изменение импульса в единицу времени равно действующей силе:

(6)

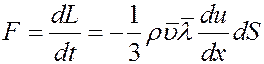
Сравнивая (6) и (1) найдем коэффициент динамической вязкости:

(7)

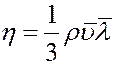
p, а

1/p. Следовательно, из (7) вытекает, что η не зависит от давления газа. Этот факт объясняется следующим образом. С уменьшением давления уменьшается концентрация молекул, а значит и их число, участвующее в переносе. Однако 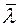при этом увеличивается. Поэтому импульс, который переносит одна молекула, так же увеличивается. В результате суммарный импульс, переносимый молекулами при данном градиенте скорости не изменяется.

Из (7) видно, что η увеличивается с ростом температуры:

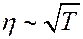
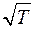
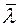
На самом деле η растет несколько быстрее чем , потому что с ростом температуры не только увеличивается скорость молекулы, но и уменьшается эффективный диаметр молекул (формула Сезерленда), что приводит к увеличению .

Теплопроводность. Если газ неравномерно нагрет, т.е. температура одной его части больше другой, то наблюдается выравнивание температуры: более нагретая часть газа охлаждается, а более холодная нагревается. Очевидно, что выравнивание температуры связано с потоком тепла от нагретой части газа к холодной.

Явление возникновения потока тепла в газе (или в любом другом веществе) называется теплопроводностью. В любом теле, в частности в газе, предоставленном самому себе, теплопроводность приводит к выравниванию температур.

Фурье установил опытами, что количество теплоты, которое передается через площадку dS за время dt в направлении нормали к площадке пропорционально градиенту температуры.

(8)

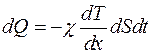
где χ – коэффициент теплопроводности. Он зависит от рода газа и условий, при которых газ находится.

Физический смысл χ: Коэффициент теплопроводности численно равен количеству теплоты, которое переносится через единичную площадку, в единицу времени при единичном градиенте температуры.

Знак «-» в правой части (8) показывает, что направление, в котором возрастает температура и направление, в котором переносится тепло противоположные, т.е. теплота переносится в направлении уменьшения температуры.

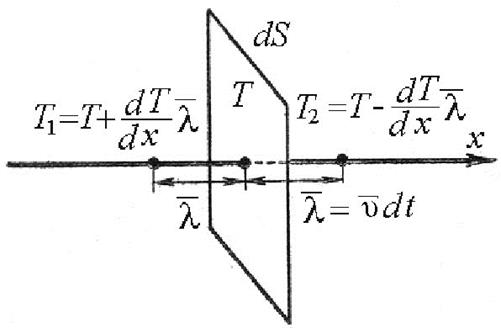
Рассмотрим площадку dS перпендикулярную оси x, вдоль которой поддерживается постоянная разность температур. Температура слева от площадки больше чем справа T₁ > T₂ (рис.2).

Рис.2. Теплопроводность газов.

Через площадку dS проходят молекулы как слева направо, так и справа налево и если давление газа везде одинаково, то число молекул, которые проходят через площадку слева и справа за время dt очевидно одинаково. Однако молекулы, которые проходят слева движутся из области с более высокой температурой, чем те, которые проходят через площадку справа.

Поэтому возникает поток теплоты, равный разности энергий переносимых молекулами слева и справа. Последние столкновения перед площадкой dS слева и справа, будут происходить на расстояниях 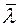, где температура слоев газа равна соответственно:

В направлении оси x двигается 1/3 всех молекул: 1/6 слева направо и 1/6 справа налево. Средняя кинетическая энергия молекул газа равна:

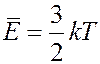
За время dt через площадку dS слева направо пройдет

молекул, каждая из которых обладает кинетической энергией

Они перенесут через площадку dS энергию:

(9)

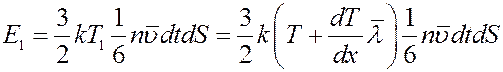
Одновременно за это же время через площадку пройдет такое же количество молекул справа налево, каждая из которых обладает энергией:

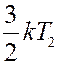
Они перенесут через площадку энергию:

(10)

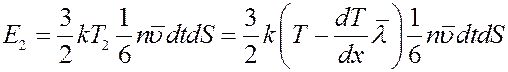
С учетом этого количество теплоты (энергия), которая переносится молекулами через площадку dS, будет равна разности кинетических энергий молекул проходящих через площадку.

(11)

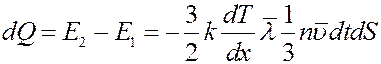
Умножим и разделим правую часть (11) на массу молекулы m и число Авогадро N_A:

(12)

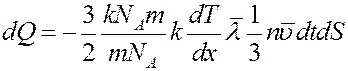
Учтем, что: mn = ρ – плотность газа, а величина

где mN_A = μ – молярная масса, c_V – удельная теплоемкость газа при постоянном объеме. С учетом этого из (12) получим:

(13)

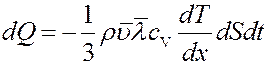
Сравнивая (13) и (8) определим коэффициент теплопроводности:

(14)

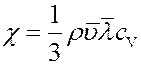
Из (14) следует, что χ не зависит от давления p по той же причине, что и η (ρ

1/p). Коэффициент теплопроводности зависит от T, так же как и η:

Однако для многоатомных газов необходимо учитывать некоторое возрастание теплоемкости c_V с увеличением температуры.

При определении коэффициентов переноса (D, η, χ) считалось, что молекулы двигаются через площадку в направлении нормали к ней. Однако это не так. Более строгие расчеты показывают, что через площадку двигается 1/4 часть всех молекул. С учетом этого:

Сравнивая выражения для коэффициентов переноса, получим связь между ними:

Любой из коэффициентов переноса, определенный экспериментально, позволяет найти среднюю длину свободного пробега молекул, следовательно, позволяет определить размеры (эффективный диаметр) молекул. Величины значений сечений молекул данного газа, определенные из различных коэффициентов переноса, совпадают и называются газокинетическими сечениями.

\|	следующая лекция ==>
Средняя длина и среднее время свободного пробега молекул. Явления переноса в газах. Диффузия.	\|	Теплопроводность и внутреннее трение при низких давлениях. Технический вакуум. Получение и методы измерения низких давлений

Дата добавления: 2015-05-21 ; просмотров: 3796 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Вязкость (внутреннее трение). Закон Ньютона. Коэффициент вязкости

Вязкость (внутреннее трение) связано с возникновением сил трения между слоями газа (жидкости), перемешивающимися друг с другом с различными по модулю скоростями.

Со стороны слоя движущегося быстрее, на более медленно движущийся слой действует ускоряющая сила и наоборот, медленно перемещающийся слой тормозит более быстро движущиеся слои газа (жидкости). Силы трения которые при этом возникают, направлены по касательной к поверхности соприкосновения слоев. С молекулярно-кинетической точки зрения причиной вязкости является упорядоченное движение слоев с различными скоростями u и хаотичного движения молекул υ.

Согласно закону Ньютона сила трения между двумя слоями газа или жидкости равна.

Эмпирическое уравнение вязкости, закон Ньютона:

где η – коэффициент вязкости; — величина показывающая, как быстро изменяется

скорость течения жидкости или газа в направлении z, перпендикулярном к направлению движения слоев (градиент скорости u), S – площадь лежащей на границе между слоями поверхности, по которой действует сила F.

Согласно 2-му закону Ньютона:

или, , тогда

Уравнение Ньютона для внутреннего трения можно представить в виде:

где Δр_им – импульс, передаваемый от слоя к слою за секунду (Δt=1 с), т.е. поток импульса через поверхность S. Знак «минус» в формуле обусловлен тем, что импульс «течет» в направлении убывания скорости u. Поэтому знаки импульса и градиента скорости u противоположны.

В формуле Ньютона минус писать нельзя, потому что она определяет одинаковый модуль двух противоположно направленных сил, с которыми слои действуют друг на друга. Кроме того нужно брать модуль градиента скорости, так как производная может иметь любой знак, а модуль силы – положительная величина.

Рассмотрим происхождение силы внутреннего трения.

Рассмотрим два соприкасающихся слоя газа толщиной Δz. Слои движутся с различными скоростями u₁ и u₂. Каждая молекула газа участвует в двух движениях: хаотическом тепловом, средняя скорость которого равна , и упорядоченном движении со скоростью потока u. Скорость потока намного меньше, чем скорость теплового движения. В неподвижном газе средний импульс молекулы равен нулю. Молекула в потоке газа обладает средним импульсом mu. При рассмотрении внутреннего трениянас будет интересовать этот импульс.

Пусть в некоторый момент времени слои обладают импульсами р_им1 и р_им2. При отсутствии внешнего воздействия на слои, их импульсы не могут оставаться неизменными, так как вследствие теплового движения происходит непрерывный переход молекул из одного слоя в другой. Попав в другой слой, молекула претерпевает столкновения с молекулами этого слоя, в результате чего она отдает избыток своего импульса другим молекулам ( если она прилетела из слоя, движущегося быстрее), либо увеличивает свой импульс за счет других молекул (если она прилетела из слоя, движущегося медленнее). В итоге импульс слоя, движущегося быстрее, убывает, а слоя, движущегося медленнее, возрастает. Следовательно, слои ведут себя так, как если бы к слою, скорость которого больше, была приложена сила, тормозящая его движение, а к слою, скорость которого меньшая, — такая же по модулю сила, ускоряющая его движение. Таков механизм возникновения сил внутреннего трения.

Через поверхность S, лежащую на границе раздела слоев, переходит в единицу времени из одного слоя в другой количество молекул, определяемое выражением:

на среднюю скорость молекул в направлении, перпендикулярном к слоям, движение слоев со скоростью u не оказывает влияния). В результате возникает в направлении от более быстрого слоя к более медленному поток импульса через поверхность S, равный:

В реальном потоке газа скорость при переходе через воображаемую границу двух слоев изменяется не скачком, а непрерывно по закону u=u(z). Будем считать, что каждая молекула, пролетающая через поверхность S, несет с собой импульс mu, определяемый скоростью u в том месте, где произошло столкновение молекулы. Это столкновение происходит на различных расстояниях от S. В среднем последнее столкновение происходит на расстоянии, равном длине свободного пробега λ. Поэтому молекулам, летящим в направлении оси z, припишем значение скорости u₁=u(z–λ), а молекулам, летящим в противоположном направлении, – значение скорости u₂=u(z+λ). Подстановка этих значений в формулу для потока импульса через поверхность S в направлении оси z дает выражение: