Поведение реального газа можно описать с высокой точностью с помощью вириального уравнения (или уравнения с вириальными коэффициентами). Идея состоит в отказе от минимального числа параметров и использовании бесконечных рядов — разложений по степеням 1/V:
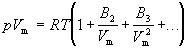
Коэффициенты B2, B3, . (которые зависят от температуры и природы рассматриваемого газа, но не зависят от плотности и давления) называются соответственно вторым, третьим, . вириальными коэффициентами. Первый вириальный коэффициент равен 1. Второй вириальный коэффициент обычно более важен, чем последующие, поскольку для большинства случаев B2 /Vm >> B3 /V 2 m >> . .
Уравнение состояния в виде бесконечного ряда (1.15) было предложено Тиссеном в 1885 г. Однако основное развитие вириальное уравнение получило в 1901 г. в работе Камерлинг-Оннеса, который рассмотрел несколько вариантов этого уравнения и предложил называть его коэффициенты вириальными.
Если подходить в вириальному уравнению только как к эмпирическому уравнению состояния, то оно имеет ряд недостатков. Например, как показывают экспериментальные данные, сходимость ряда не очень хорошая, особенно в области высокой плотности. Кроме того, при высоких плотностях для удовлетворительного описания экспериментальных данных необходимо использовать большое число членов ряда, а для этого нужно экспериментально определять большое число вириальных коэффициентов. Более того, часто тот же набор экспериментальных данных можно более точно описать с помощью других эмпирических уравнений с меньшим числом параметров. Однако исключительная важность вириального уравнения состояния заключается в том, что это единственное из известных уравнений состояния, имеющее строгую теоретическую основу. Как будет показано в главе 2, каждый вириальный коэффициент можно выразить через силы межмолекулярного взаимодействия. Так, второй вириальный коэффициент отражает парные взаимодействия, третий – тройные и т.д. Таким образом, вириальное уравнение состояния позволяет объяснить свойства газа с позиции межмолекулярных взаимодействий.
Для некоторых целей вириальное уравнение удобнее записать в виде разложения по степеням p:
Таким образом, вириальное уравнение является примером того, когда простое выражение (в данном случае pVm = RT) представляет собой только первый член ряда разложения по степеням переменной (в данном случае p или Vm).
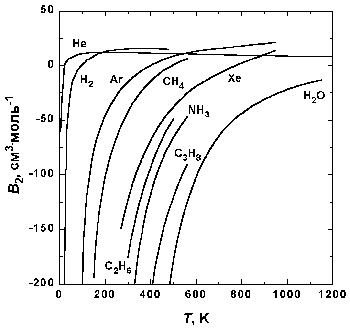
Рис.1.5. Зависимость второго вириального коэффициента некоторых газов от температуры.
На рис. 1.5 представлена зависимость второго вириального коэффициента от температуры для некоторых газов. При низких температурах B2 n-1 . Таким образом, уравнение Ван-дер-Ваальса качественно правильно передает температурную зависимость второго вириального коэффициента при низких температурах (при низких температурах B2
| [предыдущий раздел] | [содержание] | [следующий раздел] |


Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору
Видео:Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Вириальные коэффициенты.







Видео:Лекция №4. РЕАЛЬНЫЕ ГАЗЫСкачать

Вириальные коэффициенты.
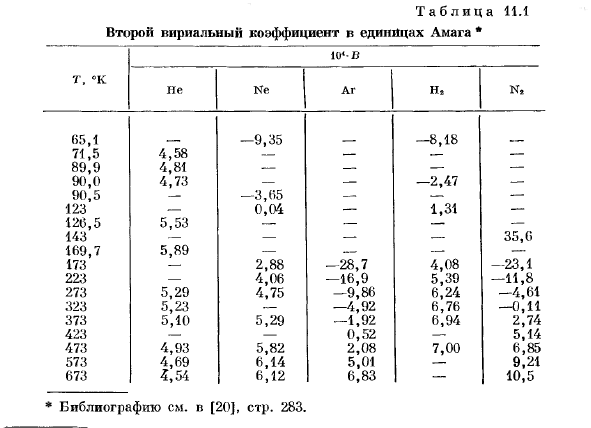
- Вириальные коэффициенты. Сначала мы ограничиваемся изучением чистых газов, а затем переходим к смешанным газам. Высокоточное давление газа можно представить в виде ряда порядка 1 / v (а молярный объем равен V / p: Где B, C-только функция температуры. Количество терминов, необходимых для описания точек экспериментальных данных в пределах точности измерений, варьируется от 2 до 4 в зависимости от рассматриваемого интервала температур и давлений. Коэффициент/?, Таких как C, 2й, 3й и т. д., называется коэффициентом вириала.
nWrf ВР Во-вторых, коэффициент virpal имеет размерность объема на 1 моль. А в качестве единицы измерения объема часто выбирается единица мага а. Это, по определению, равно молярному объему газа при 0°С и 1 атм. Точное значение этой единицы зависит от природы рассматриваемого газа, но составляет приблизительно 22,4×10 см * / моль. И недавно, Б часто представлены непосредственно в СМ ^ / моль.
Для газа, который немного отличается от идеального, достаточно ограничить его первыми 2 участками разложения. Людмила Фирмаль
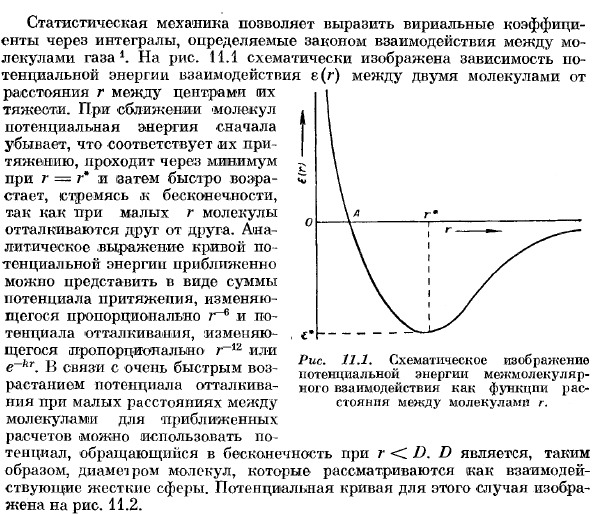
Внутри таблицы. 11.1 показано значение 2-го вириального коэффициента для некоторых нормальных газов в зависимости от температуры. 2-й вириальный коэффициент при низких температурах отрицательный, он увеличивается с температурой и становится положительным при высоких температурах. Температура при B = 0 называется температурой кипения. В статистической механике вириальный коэффициент может быть выражен в интегралах, которые определяются законом взаимодействия молекул газа 1.На рис. 11.1 схематично показана зависимость потенциальной энергии взаимодействия E (g)между 2 молекулами от расстояния r между центрами их притяжения. — При приближении молекулы сначала уменьшается потенциальная энергия. Это соответствует их притяжению и проходит минимальное значение при r = r * l, а затем быстро возрастает.
Аналитическое выражение потенциальной энергии кривой можно приближенно представить в виде суммы привлекательный потенциал, который изменяется пропорционально R-6 и отталкивающий потенциал, который изменяется пропорционально р〜р или Е〜кг. Очень быстро Рисунок 11.1. схематическое представление потенциальной энергии межмолекулярного взаимодействия как функции расстояния между молекулами g. Для приближенных расчетов можно использовать потенциал до бесконечности в растении r ® .
Из показаний B (T) при различных температурах находим e ® , особенно r *и минимальную глубину e. дело в том, что B (T) отрицательно при низких температурах и положительно при высоких температурах заключается в том, что интегральное значение уравнения низкой температуры (11.15) в значительной степени определяется значением R, где e ® отрицательно, а при высоких температурах e ® положительно, область r играет важную роль. Формула для 3-го вириального коэффициента была получена de Boerom2 и Montroll. М и 3 основная свободная энергия ослабляет нсидеалпого газа, что выражается во втором вириальном коэффициенте. Применяя (7.11) и (11.14), получаем Гонка 11.2.
Принципиальная схема потенциальной энергии межмолекулярного взаимодействия (приближение твердой сферы). (11.16) (11.17) Химический потенциал идеального газа определяется по формуле (10.11 Где p16-давление, создаваемое идеальным газом n моль объема T7, so= hRT / ’ V. By подставляя эти выражения для (11.17)、 Широта / ЗРТ * 2 РТРС с = ХТ(г)+ RTln-+. (11.18) Молярная энтропия газа определяется по формуле S 1 (dF, a lH / m dB Где s и d-энтропия тех же T и V, Если газ ведет себя как идеальный газ. Это значение может быть вычислено по формуле (11.19), если известно уравнение состояния и$измеряется калорически (см. Главу 9). таким образом, было найдено исправление, которое использовалось в численных расчетах Sec. JX.
Вместо разложения ряда давлений газа по степеням 1 / y объем газа можно представить в виде ряда стенок. В = ^(1 + б ’п + с’ Р2 + …(11.20).) Где, B’, C1… — функция температуры. Для неидеальных газов вы можете игнорировать все термины, начиная с p2, и вычислить свободную энергию Гиббса. ДФР = шь’/’ / / >、* В-В [Д = firmb И согласно (11.8)、 С. С. Г (т, п, н)= КЦ ^(л р, п)+ м ж «нртб» ’ДП = Г(Т, Пина)+пПТВ’р. ^ п *(11.21) Для однокомпонентных систем Г = п я,(11.22) И затем… li (T, p)= p * BT, p)+ R TV’R. используйте (11.23) (10.11), чтобы получить p = ^ t(71) 4-R7-In p + bBTp. (11.24) Коэффициент (11.20)/?’, С ’ г…
- Может быть выражен вириальным коэффициентом формулы (-11.13).Это можно легко проверить на примере 2-го дополнительного коэффициента. Из уравнения (d ’ 1.13)、 R T v С другой стороны, (11.20) ПВ = 1 + и P +. (л, б Р Т Если вы игнорируете членов высшего порядка、 Б = р б ’ Ри. Итак, используя правильное приближение, вы можете написать: C = попадание. В этом приближении вместо (11.20)、 R5T /. 。 П. С. Или В = ВЛД + Б Таким образом, 2-й вириальный коэффициент приблизительно равен разнице между молярным объемом фактического газа и идеального газа при одинаковой температуре и давлении. Наконец, рассмотрим смесь 2 слабых и неидеальных газов, которые не взаимодействуют химически. Формулу (11.14) следует записать в более общем виде, так как необходимо учитывать взаимодействие между идентичными и разными молекулами. ю | л р. г р = ±(Vishch + 2Vapm + Вла).
Фактор B относится к взаимодействию между молекулами типа 1, # 12-к взаимодействию между неравными молекулами 1 и 2, а Vuj-к взаимодействию между молекулами типа 2.При переходе к мольной концентрации 、 Р = + 2JW * + м ^). (11.27) к V ^ Если мы сравним полученную формулу с (11.14), то увидим, что 2-й коэффициент вири-ал смеси можно определить как функцию 2-го порядка от молярной доли. Б = Бин + 2Bi2xtx2 + BiXxi(11.28) Следует подчеркнуть, что для определения 2-го вириального коэффициента смеси недостаточно знать вириальный коэффициент каждого чистого газа, а также необходимо знать дополнительно.
В этом случае коэффициенты в ч, статистической механики вытекает уравнения, например, (11.15) N 0 КТГ(Т)= — $(1-е-MrVkT)^(11.29) И Где eig ® — энергия взаимодействия между молекулами 1 и 2.So по крайней мере, как правило, исследование вириального коэффициента двойной газовой смеси позволяет определить не только энергию взаимодействия En и 822 между молекулами одного типа, но и энергию 6i2.Однако в этом направлении проделано мало работ2.
Как и раньше, вы можете найти свободную энергию смеси. Людмила Фирмаль
/ «=я- + кг * »» ’(11.30) И химический потенциал обоих ингредиентов: 1 * 1 = я я = | * я + 2Р » — й —- V dhz) Tf v>Пж ^ V Из и _ _ _ Впщ + V9Up2 !12. Ф-О Г ИД Л — М-4- = () = М2 + 2R71″ DN2 по)Т, Т (11.31) Используя последнее уравнение (10.34) t, можно также придать следующий вид: Я… = г(т)+ Р71 в + 2RT (11.32)) В. 1 Фаулер и Гуггенхайм [20), стр. 2. М. См. Newitt. Конструкция установки высокого давления (Оксфорд.1940); И. А. Beafr-галстук, У. Stokmayer. Ж. Chcm. Физика., 10, 473(1942); K. J. Lumbeck, A. J. II. Boerboom Physica, 17, 7G(1951).




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Уравнение Ван-дер-Ваальса | Газы.Молекулярно-кинетическая теория | Химия (видео 8)Скачать

Уравнения состояния реальных газов
Вопрос №1
Идеальный газ. Законы идеальных газов
Идеальным называется газ, у которого объемы молекул бесконечно малы и отсутствуют силы межмолекулярного взаимодействия. Молекулы идеального газа представляют собой материальные точки, взаимодействие между которыми ограничено молекулярными соударениями.
Любой реальный газ тем ближе к идеальному, чем ниже его давление и выше температура. Например, окружающий нас воздух можно считать идеальным газом. Понятие идеального газа и законы идеальных газов полезны в качестве предела законов реального газа.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
На практике часто приходится иметь дело с газами при невысоких давлениях, поэтому расчеты различных термодинамических процессов с достаточной степенью точности можно проводить по уравнениям идеального газа.
Закон Авогадро
Согласно этому закону, все газы при одинаковых температурах и одинаковом давлении содержат в одном и том же объеме одинаковое число молекул. Большую техническую значимость имеет следствие из закона Авогадро: объемы киломолей различных газов равны, если они находятся при одинаковых температурах и давлениях. При нормальных физических условиях (Т= 273,15 К, р = 760 мм рт. ст.) объем киломоля любого вещества равен Vµ=µν=22,4 м 3 /кмоль.Напомним, что киломолем называется количество вещества в килограммах, численно равное его молекулярной массе.
Этот закон был открыт независимо друг от друга английским физиком Р. Бойлем и французским ученым Э. Мариоттом. Ими было доказано, что при постоянной температуре газа произведение давления газа на его объем есть величина постоянная, т.е. при
рV= const и рv = const.
Закон Гей-Люссака
Этот закон устанавливает, что если в процессе нагрева или охлаждения газа давление подцерживается постоянным, то объем изменяется пропорционально абсолютной температуре, т.е. если
Р = const, то и v/ Т = const.
Если же мы рассмотрим процесс нагрева или охлаждения газа в сосуде постоянного объема (v= const), то р/Т = const.
Уравнение состояния идеального газа
Для 1 кг газа Клапейроном установлено уравнение состояния рv = RT, в котором газовая постоянная Rимеет для каждого газа свое постоянное значение. Измеряется Rв Дж/кг-К и имеет вполне определенный физический смысл — это работа, совершаемая 1 кг газа при его нагреве на один кельвин при постоянном давлении. Для газа с произвольной массой M/(кг) уравнение состояния имеет вид
Для одного киломоля вещества уравнение состояния (получено Д.И. Менделеевым) имеет вид рVµ =µRT, где µR— универсальная газовая постоянная, которая одинакова для всех газов и равна 8314 Дж/кмольК.
Во всех этих уравнениях давление подставляется в Па, температура — в К, объем — в м 3 и удельный объем — в м 3 /кг.
В резервуаре объемом 10 м 3 находится азот при избыточном давлении 100 кПа и при температуре 27 °С. Атмосферное давление равно 750 мм рт. ст. Требуется найти массу и плотность азота.
Выразим атмосферное давление в паскалях: рб = 10 5 Па.
Абсолютное давление газа равно:p =ри +рб = 100 • 10 3 + 10 5 = = 2 • 10 5 Па.
Газовая постоянная азота равна (µ = 28 кг/кмоль)
R = 8314/28 = 297 Дж/кгЧК. Масса газа равна
М =рV/RT= 2*10 5* 10/297 • (273,15 + 27) = 22,43 кг.
р = M/V= 22,43/10 = 2,243 кг/м 3 .
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
РЕАЛЬНЫЕ ГАЗЫ
Свойства реальных газов
Свойства реальных газов значительно отличаются от свойств идеальных газов, причем отличия тем значительнее, чем выше давление и ниже температура газа. Это объясняется тем, что молекулы реальных газов имеют конечный объем и между ними существуют силы межмолекулярного взаимодействия. Уравнение состояния 1 кг реального газа имеет вид
где z= φ(р, T) — коэффициент сжимаемости, который может быть как больше, так и меньше единицы.
При проведении термодинамических расчетов с реальными газами нужно учитывать зависимость внутренней энергии, энтальпии и теплоемкости не только от температуры, но и от давления газа. При одном и том же давлении какое-либо вещество в зависимости от температуры может находиться в разных состояниях.
Из физики известно, что любое вещество может находиться в твердом, жидком или газообразном состоянии. Эти состояния будем называть фазами, а процесс перехода из одного состояния в другое — фазовым переходом.
При определенных условиях могут существовать одновременно две фазы вещества, например, лед и жидкость, пар и жидкость. Если пар и жидкость находятся в состоянии равновесия, то пар называется насыщенным.
У всех веществ фазовые переходы происходят при определенных физических параметрах, поэтому рассмотрение свойств реальных газов можно начать на примере вещества, которое является основным рабочим телом в циклах тепловых электростанций, в том числе и атомных. Этим рабочим телом является вода, и не только потому, что она относительно дешева и нетоксична, а потому, что она обладает благоприятными для работы термодинамическими свойствами.
Рассмотрим диаграмму «v—p» воды и водяного пара, на которой изобразим границы между фазами (рис. 1.1). В области а находится в равновесии смесь льда и некипящей воды, в области Ь находится некипящая вода, в области с находится смесь кипящей воды и водяного пара, в области d— перегретый водяной пар. Прямой 1-2 показан изобарный процесс подвода теплоты.
Показанные на рис. 1.1 кривые называются пограничными; кривые, ограничивающие с двух сторон область с, называются левой и правой пограничными кривыми. Им соответствуют кипящая вода (левой) и сухой насыщенный пар (правой). Область между этими кривыми называется областью влажного насыщенного пара — в этой области находятся в равновесии сухой насыщенный пар и кипящая вода. Смесь сухого насыщенного пара и кипящей воды называют влажным насыщенным паром. Масса влажного насыщенного пара равна
где М’ — масса кипящей воды и М» — масса сухого насыщенного пара.
В дальнейшем все параметры, относящиеся к кипящей жидкости, будут иметь индекс «штрих» (р’, h’и т.д.), а все параметры, относящиеся к сухому насыщенному пару,— индекс «два штриха» (р’, h» и т.д.).
Температуру и давление насыщенного пара принято обозначать Тн и рн. В то же время в ряде литературных источников их обозначают Тs и рs (буква s является первой буквой английского слова sаturation — насыщение). Отношение массы сухого насыщенного пара к общей массе влажного насыщенного пара называется степенью сухости и обозначается х. Ясно, что на левой пограничной кривой х = 0, а на правой — х = 1. Разность <1-х) называется степенью влажности.
Чем выше давление пара, тем меньше расстояние по горизонтали между левой и правой пограничными кривыми, а при определенном давлении пара эти кривые смыкаются. Точка, в которой исчезают различия в свойствах кипящей жидкости и сухого насыщенного пара, называется критической (точка к на рис. 1.1).
Термические параметры различных веществ в критической точке различны. Эти параметры для ряда химических веществ приведены в табл. 1
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Таблица 1 Критические параметры веществ
| Вещество | Tкр, К | pкр,МПа | ρкр, кг/м 3 |
| Азот N2 | 3,40 | ||
| Водород Н2 | 33,2 | 1,29 | |
| Водяной пар H2O | 647,12 | 22,115 | |
| Кислород О2 | 5,05 | ||
| Ртуть Нg | — | ||
| Диоксид углерода СО2 | 7,38 |
При сверхкритическом давлении не может быть влажного насыщенного пара. Если давление пара больше критического и постоянно по величине (р > ркр), то при подводе (или отводе) теплоты физические параметры (удельный объем, энтальпия и др.) меняются плавно, в то же время наблюдается резкое изменение тепло-емкостей сp исvв тех процессах, где сверхперегретая вода переходит в сверхперегретый водяной пар.
Уравнения состояния реальных газов
Известно значительное число уравнений состояния реальных газов, и одна из самых удачных попыток была сделана Ван-дер-Ваальсом, который получил уравнение в виде
Слагаемое a/v 2 учитывает внутреннее давление, обусловленное силами взаимодействия молекул газа, а величина b— уменьшение объема, в котором движутся молекулы реального газа. Если по этому уравнению находить величины удельных объемов реальных газов, то уравнение (1) имеет три действительных корня при Т Ткр . Точность вычислений по этому уравнению невелика.
В самой общей форме уравнение состояния реальных газов имеет вид
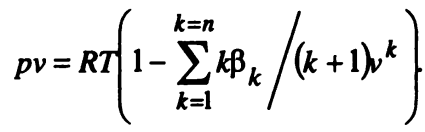
где 𝛽k — вириальные коэффициенты, зависящие от температуры газа.
Число членов ряда в уравнении (2) может быть достаточно велико, поэтому расчеты по этому уравнению вызывают значительные трудности.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
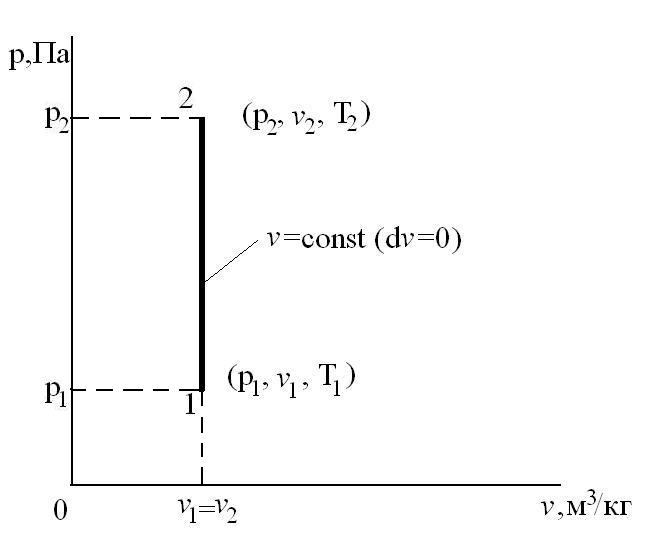
Изохорный процесс – это процесс сообщения или отнятия теплоты от газа при постоянном объеме v=const.
Этот процесс используется как подготовительный процесс в циклах.
Соотношение между параметрами для конечного участка процесса 1-2 определяется законом Шарля: 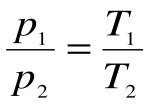
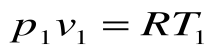
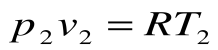
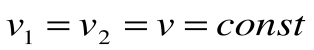
Поскольку работа расширения в этом процессе равна нулю: 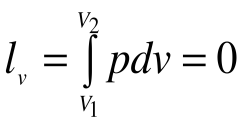
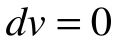
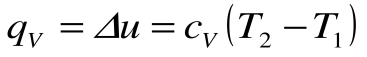
Таким образом, подведенная к газу в изохорном процессе теплота целиком идет на увеличение его внутренней энергии. Для ТП 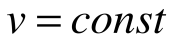
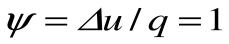


| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
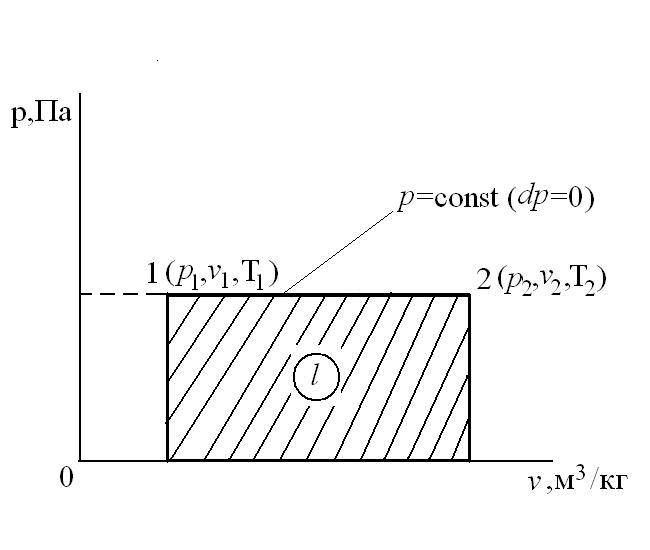
Изобарный процесс – это процесс сообщения или отнятия теплоты от газа при постоянном давлении р=const.
Соотношение между параметрами в процессе р=const: 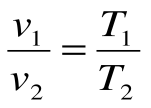


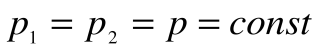
Работа расширения 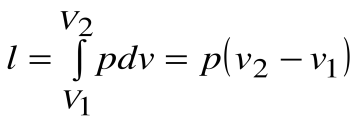
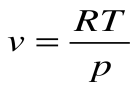
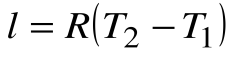
Следовательно, удельная газовая постоянная R— это работа, совершаемая 1кг газа в процессе p=const при его нагревании на один градус. Размерность R: Дж/кгК. Уравнение 1-го закона термодинамики в этом случае имеем вид:
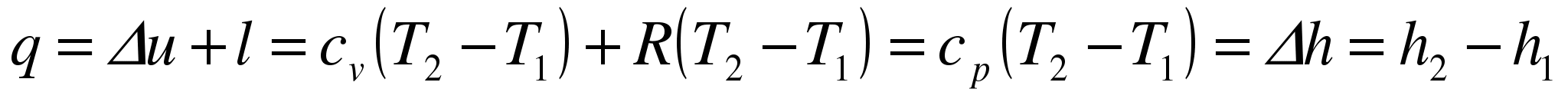
Таким образом, вся теплота, подведенная к газу в изобарном процессе, расходуется на увеличение его энтальпии.
Коэффициент распределения теплоты в процессе р=const равен:
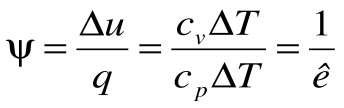
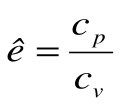
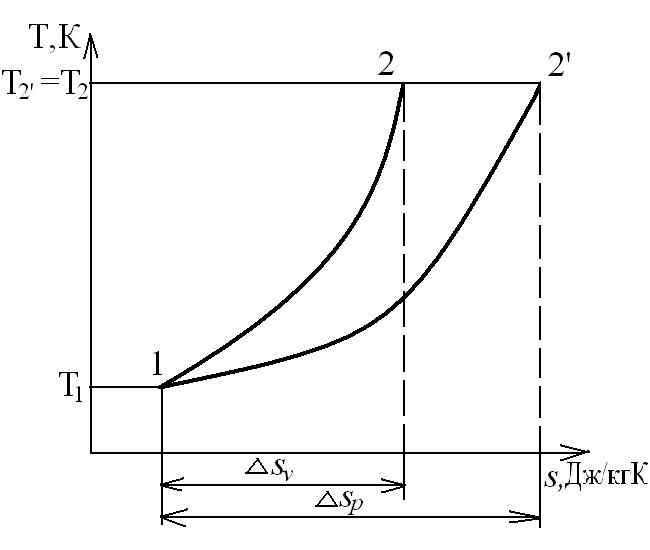
В T-s координатах взаимное положение изобары и изохоры имеет вид:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
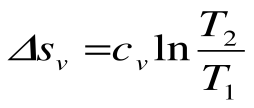
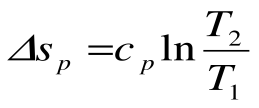
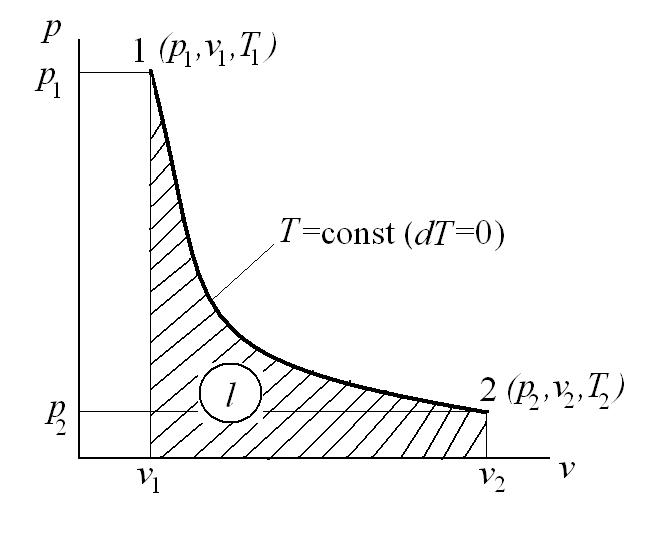
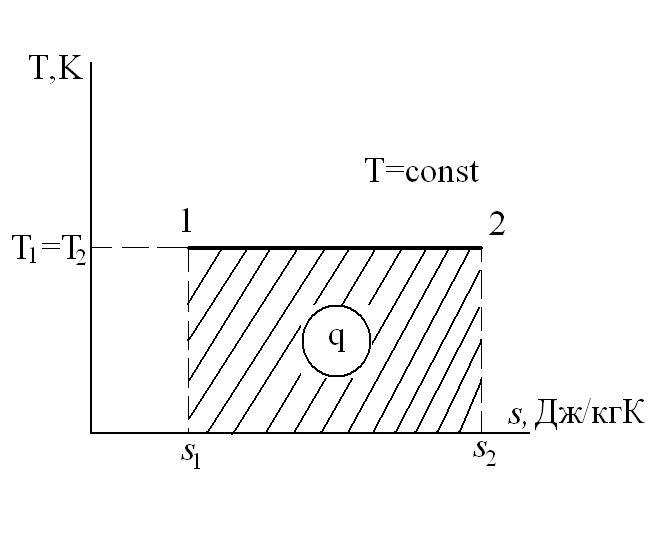
Изотермический процесс – это процесс сообщения или отнятия теплоты от газа при постоянной температуре
При Т=const из уравнения состояния 
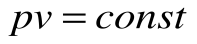
Тогда 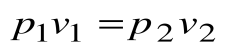
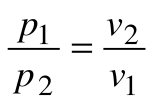
Из уравнения 1-го закона термодинамики 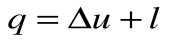
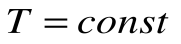
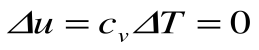
Изменение энтальпии в процессе T=const равно:
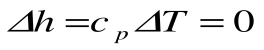
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Работа расширения 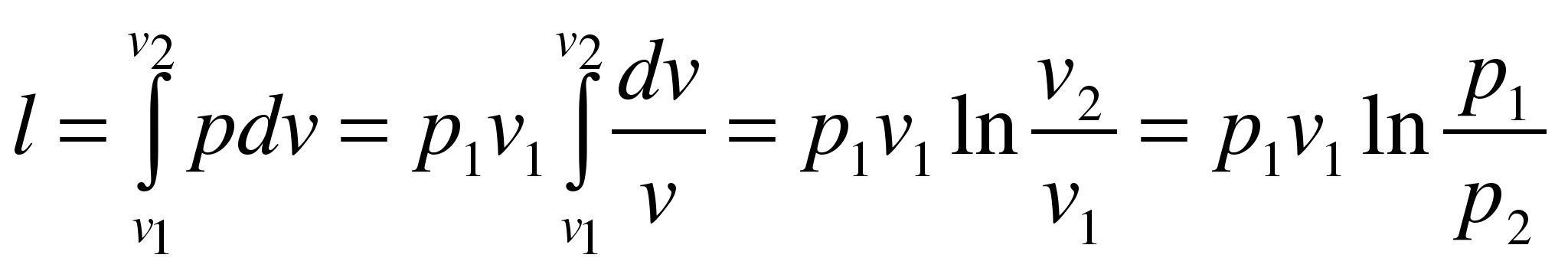
Коэффициент распределения теплоты
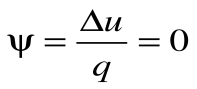
Тогда теплоемкость 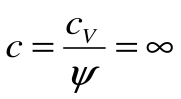
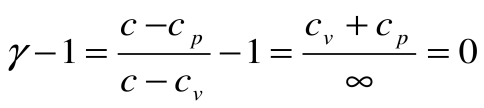
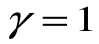
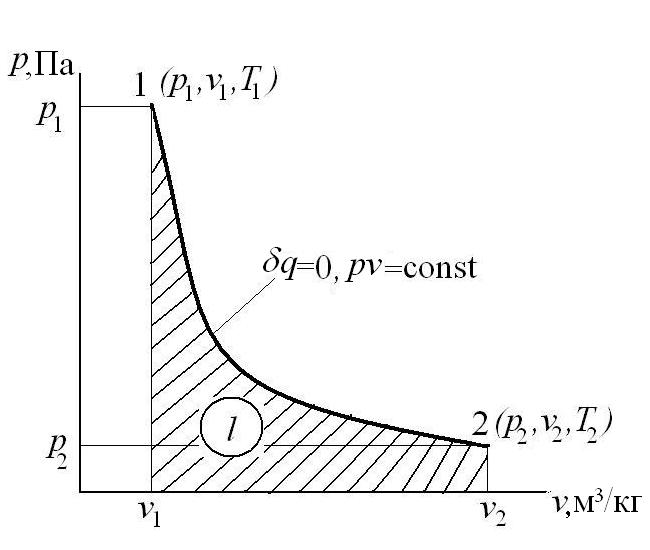
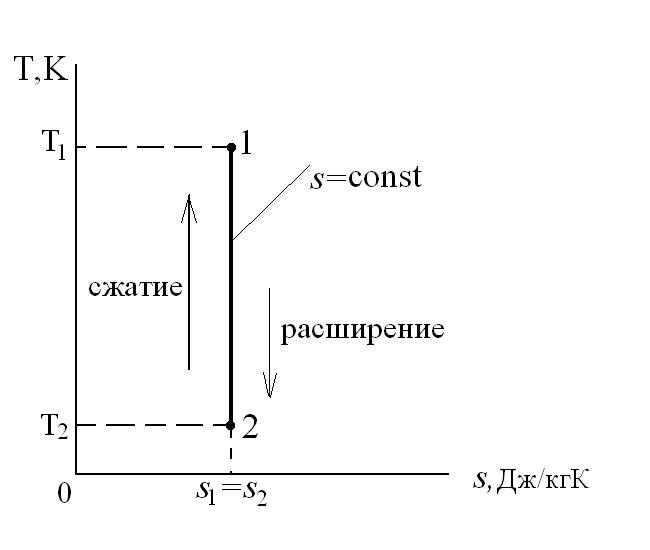
Адиабатный процесс – это процесс, протекающий без внешнего теплообмена, т.е. q=0 и 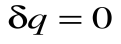
Если записать для этого случая уравнения 1-го закона термодинамики в виде:
1. 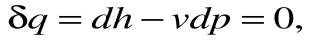
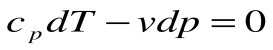
2. 
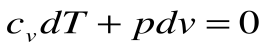

Тогда после интегрирования выражения 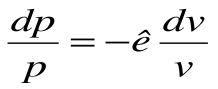

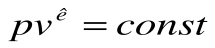
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
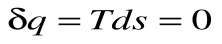
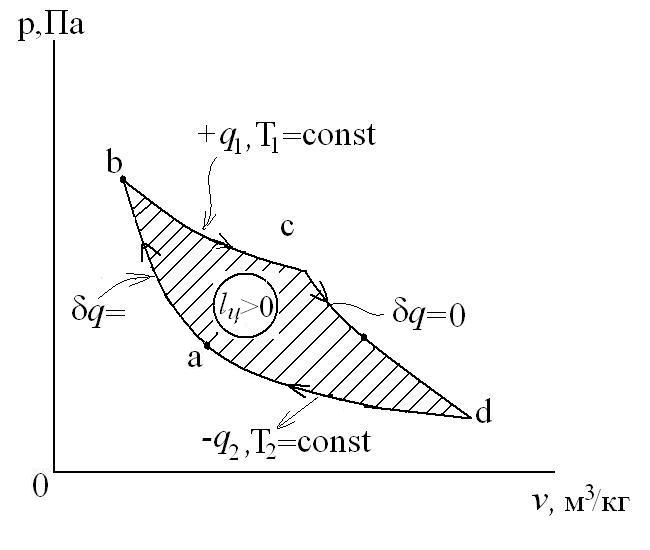
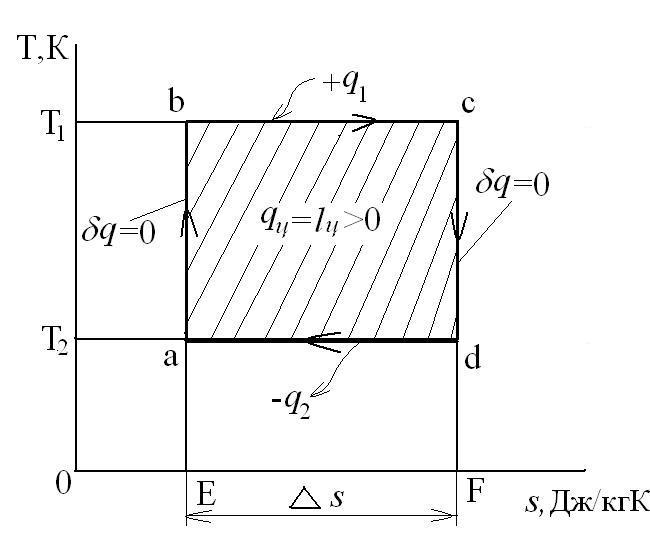
Для теплового двигателя цикл Карно – прямой цикл, состоящий из двух адиабат и двух изотерм, а для тепловых трансформаторов используется обратный цикл Карно. Тепловые машины, работающие по циклу Карно, имеют наибольшие значения термических кпд по сравнению с любым другим циклом при одинаковых предельных температурах цикла Т1 и Т2.
Рассмотрим прямой цикл Карно.
Графически в p-v и T-s координатах этот цикл можно представить в виде:
где ab – адиабатное сжатие ТРТ;
bc – подвод теплоты q1 в изотермическом процессе при Т1=const;
cd – адиабатное расширение ТРТ;
da – отвод теплоты 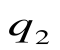
q1 = площадь bсFEb – теплота, затраченная на совершение цикла 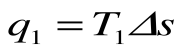
q2 = площадь adFЕa – теплота, отведенная в холодильник 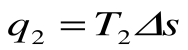
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Тогда термический кпд прямого цикла Карно будет равен:
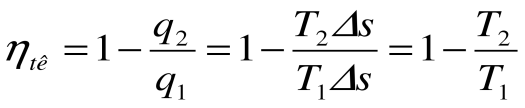
Таким образом, термический кпд цикла Карно зависит только от предельных температур источника и холодильника и не зависит от рода рабочего тела. (Первая теорема Карно). Температура Т1 и Т2 являются основными параметрами цикла Карно, которые полностью определяют этот цикл.
При Т1=Т2 термический кпд цикла Карно 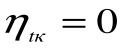
При Т2=0 или Т1= 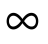
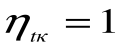
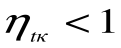
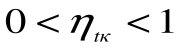
Любое заключение, вытекающее из анализа прямого цикла Карно, можно рассматривать как формулировку второго закона термодинамики.
В двух разобщенных между собой теплоизолированных сосудах А и В содержатся газы, в сосуде А – аргон, в сосуде В– водород, объем сосуда А– 150 л, сосуда В – 250 л. Давление и температура аргона – р1, t1, водорода – р2, t2. Определить давление и температуру, которые установятся после соединения сосудов и смешения газов. Теплообменом с окружающей средой пренебречь
💥 Видео
Урок 195. Изотермы реального газаСкачать

Реальные газы. Изотермы Эндрюса и Ван-Дер-Ваальса. Метастабильные состоянияСкачать

Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Лекция №7 "Реальный газ"Скачать

Идеальный и реальный газ | Газы.Молекулярно-кинетическая теория | Химия (видео 7)Скачать

Плотников Г. С - Элементы строения вещества - Свойства реального газа (Лекция 3)Скачать

Лекция 9Скачать

Урок 166. Предмет термодинамики. Внутренняя энергия телаСкачать

Семинар №6 "Реальные газы. Эффект Джоуля-Томсона. Уравнение Бернулли." (Попов П.В.)Скачать

Лекция №6 "Реальные газы" (Попов П.В.)Скачать

Селиверстов А. В. - Молекулярная физика - Семинар 26Скачать

Лекция №8 "Эффект Джоуля-Томсона. Элементы теории вероятностей"Скачать

Лекция №7 "Течение газов" (Попов П.В.)Скачать

Дросселирование газов и жидкостей. Температура после дросселирования. Обучение персоналаСкачать

Лекция №7 "Уравнение Ван-дер-Ваальса. Гидродинамика" (Булыгин В.С.)Скачать

Статистическая физика. Лекция №10 ЭН-31,32,33,36 16.11.2020Скачать

Гидромеханические процессы. Часть 1. Уровень: базовый.Скачать