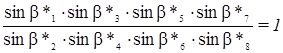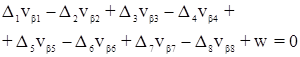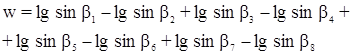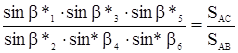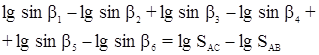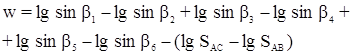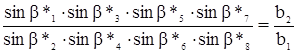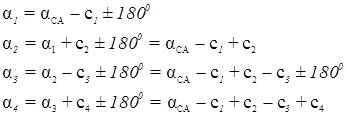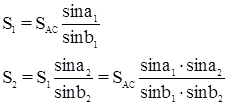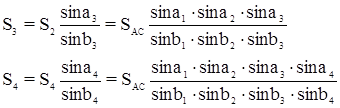Рассмотрим условные уравнения, возникающие при уравнивании углов триангуляции. При этом углы редуцированы на плоскость проекции Гаусса-Крюгера и исправлены за центрировку прибора и редукцию визирных целей.
8.1.1 Условие фигур. Сумма измеренных углов в замкнутой фигуре (например, в треугольнике) должна быть равна теоретической.
8.1.2 Условие суммы углов (условие станции). Условие возникает при измерении на станции углов между смежными направлениями и углов, являющихся суммой измеренных углов.
8.1.3 Условие горизонта. Возникает в случаях, когда на станции измерены углы с замыканием горизонта.
8.1.4 Условие полюса (боковое условие). Полюсное условие заключается в требовании, чтобы длина стороны, вычисленная двумя независимыми путями из решения треугольников сети, имела одно и тоже значение.
Примем, что Di = D lg sin bi – изменение lg sin bi при увеличении угла bi на 1”.
8.1.5 Условие исходных дирекционных углов (азимутальное условие). Условие возникает в сети, в которой две или более сторон сети имеют значения дирекционных углов, не подлежащие изменению при уравнивании.
При этом выбор ходовой линии не имеет значения. Частный случай:
8.1.6 Условие базисов возникает в случаях, когда в сети имеется две или более сторон, длины которых не подлежат изменению в процессе уравнивания. Условие базиса заключается в требовании, чтобы длина одной исходной стороны, полученная от другой исходной стороны решением треугольников совпадала с заданным ее значением.
8.1.7 Условие координат возникает в том случае, если в сети имеется два и более разобщенных между собой исходных пункта с координатами, не подлежащими изменению при уравнивании. Для составления уравнений координат из сети выделяют простую и наиболее короткую цепь треугольников, соединяющих два исходных пункта.
,
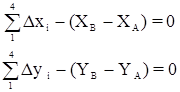
где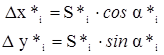 
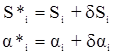
— приращения координат по ходовой линии.
.
С учетом малости поправок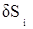 
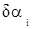
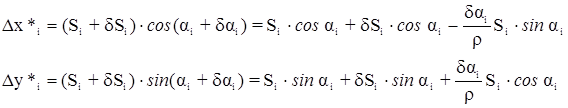
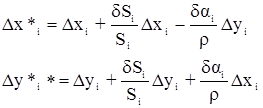
и 
можем записать:
,
,
где 
— вычисленные приращения координат по неуравненным значениям Si и ai.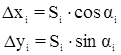
,
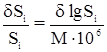
где d lg Si – изменение lg Si, соответствующее поправке 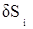и выраженное в единицах 6-го знака логарифма;
М = 0,43429 – lg e – модуль натуральных логарифмов.
.
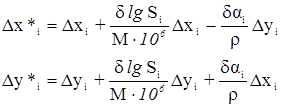
Подставим эти уравнения в исходные условные уравнения и получим:
,
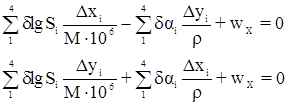
где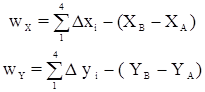 
— невязки в приращения координат.
Выразим длины и дирекционные углы ходовой линии через измеренные углы треугольников сети триангуляции:
Из этого следует, что dai и dSi независимы, так как ai вычисляются через промежуточные углы ci, а стороны Si вычисляются при помощи связующих углов ai и bi. Независимость поправок dai и dSi существенно упрощает составление условных уравнений координат. Определим поправки:
d lg S2 =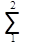 
<Dai vai — Dbi vbi>
d lg S3 =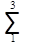 
<Dai vai — Dbi vbi>
d lg S4 =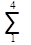 
<Dai vai — Dbi vbi>
Подставляя dai и d lg Si в условные уравнения получим в окончательном виде:
где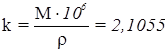 
;
xi, yi – приближенные координаты в км;
Dai, Dbi – изменения lg sin ai и lg sin bi, выраженные в шестом знаке lg;
Дата добавления: 2016-06-02 ; просмотров: 2639 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Математика | Параметр. Система уравнений с параметромСкачать
Лекции по дисциплине Геодезия (стр. 4 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 |
Тогда квадратичный коэффициент 
получится равным:
, то есть длине хода.
Нормальное уравнение коррелат примет вид:
, (60)
(61)
Коррелатные уравнения поправок в общем виде выглядят следующим образом: 
. Перенесём 
в конец формулы и получим формулу 62 подставляя раннее установленные значения :
; 
; 
, поэтому
(62)
Вычисление поправок контролирует условное уравнение оправок 
, или
.
Далее вычисляют уравненные значения превышений
.
Контролем является та же функция (то есть условное уравнение связи), но от уравненных значений 
.
Затем вычисляются отметки определяемых пунктов
,
завершая вычисление контролем
1 Уравнивание нивелирной сети коррелатным способом
Дана нивелирная сеть
Рисунок 10 – Схема нивелирной сети
— исходные пункты;
— отметки исходных пунктов;
— определяемые пункты, отметки которых необходимо найти;
— измеренные превышения;
— длины секций;
— направление превышений.
Уравнивание нивелирной сети начинают с подсчета числа независимых полигонов, в которых возникают геометрические условия. Число условий определяется числом избыточных измерений, которое подсчитывается по формуле 
или по формуле 
.
Для сети, представленной на рисунке 10, число измеренных превышений 
, число необходимых измерений 
— равно количеству определяемых пунктов. Число замкнутых полигонов 
, а число исходных пунктов 
. Таким образом 
.
Достраивают сеть до 
полигонов в соответствии с рисунком 11, выбирая вариант с меньшим числом измерений и составляют схематический чертеж сети полигонов. В данном случае необходимо достроить еще один полигон.
 |
Рисунок 11 – Схематический чертеж полигонов
На чертеже указывают номера полигонов римскими цифрами, начиная с существующих, и стрелкой направление суммирования превышений в полигонах – в любую сторону, но одинаковое для всех полигонов. Например, по часовой стрелке, как указано на рисунке 11. На пунктире указывают направление (в любую сторону) и через отметки исходных пунктов вычисляют истинное превышение по ходу, отмеченному пунктиром 
( по направлению стрелки на пунктирной линии). Для данного случая Н1 – это отметка конечного репера, а Н2 – отметка начального репера. Если для другой сети построено несколько новых полигонов, то вычисляются hист и для них.
Условные уравнения связи (функции от измеренных величин) для данной сети имеет вид:
; (63)
Сумма измеренных превышений по замкнутому полигону, с учётом направлений, равна невязке.
Их число , то есть в данном случае две функции от измеренных величин. Правило их составления следующее: если направление обхода полигона совпадает с направлением суммирования превышения в полигоне, то ставится знак «+», если не совпадает – знак «-».
В достроенных полигонах превышение 
участвует в вычислении невязок, для того чтобы невязки всех полигонов определялись однообразно: как сумма всех превышений в полигоне. Это превышение не уравнивается, то есть поправки ищут только для измеренных превышений.
Согласно общей теории уравнивания, составляют нормальных уравнений коррелат (для данной сети их два):
(64)
где 
— неизвестные коррелаты, которые необходимо найти из решения системы (64);
— невязки полигонов, вычисленные в результате составления условных уравнений связи (63).
Далее вычисляют значения коэффициентов нормальных уравнений коррелат. Если Веса измеренных превышений определяют по формуле:
,
то обратный вес
.
Коэффициенты при поправках условных уравнений поправок 
(для данной сети и возможно 
и т. д.) вычисляют как частные производные от функций 
по результатам измерений 
:
; 
.
Используя систему (63) получим:
; 
; 
;
; 
; 
; 
; 
; 
; 
.
Таким образом коэффициенты 
(и т. д.) равны +1, -1, 0.
Вычисленные коэффициенты условных уравнений записывают по столбцам в таблицу 4.
Таблица 4 — Коэффициенты условных уравнений
Затем вычисляют значения коэффициентов нормальных уравнений коррелат:
;
.
Таким образом, в общем случае квадратичные коэффициенты равны периметрам соответствующих полигонов. Соответствие происходит по буквам — первому полигону; — второму полигону и т. д. Неквадратичные коэффициенты принимаются равными длине стороны между соответствующими полигонами со знаком «-». Если общей стороны у полигонов нет, то коэффициент равен нулю.
Из решения системы нормальных уравнений находят коррелаты 
, а по ним – поправки.
Для 
коррелатные уравнения поправок в общем виде 
.
Каждому полигону соответствует своя коррелата: 
— первому полигону; 
— второму.
В результате находим поправки:
Число поправок 
по числу измерений.
Различают поправки в превышения для несмежной и смежной стороны. Для несмежной стороны поправка равна произведению длины стороны на коррелату своего полигона со знаком «+», если направленеи превышения, для которого ищется поправка, совпадает с направлением обхода полигона, и «-» — если не совпадает.
Для смежной стороны поправка равна произведению длины стороны на разность коррелат полигонов, в которые она входит; причем на первое место ставится коррелата того полигона, в котором направления превышения и обхода полигона совпадают.
Вычисление поправок контролируется составленеим 
условных уравнений поправок:
— в общем виде:
(65)
— или для конкретных :
(66)
Как видно, знаки у поправок те же, что и у превышений в условных уравнениях связи. По формулам (66) осуществляется контроль вычисления поправок, который заключается в том, что сумма поправок по полигону с учетом направлений равна невязке полигона с обратным знаком. Уравненные превышения вычисляются по формуле
(67)
Для контроля вычисления уравненных превышений составляют условные уравнения связи, те же функции, но от уравненных значений:
; (68)
По уравненным превышениям находят отметки определяемых пунктов. Оценку точности выполнят по формуле:
(69)
где 
— СКО единицы веса.
Так как 
,
где 
— ошибка на 1 км хода.
, 
, то 
, то есть средняя квадратическая ошибка превышения на 1 км хода по результатам уравнивания равна СКО единицы веса.
Должны быть выполнены следующие требования: ≤ 5 мм для III класса нивелирования и ≤ 10 мм для IV класса.
1 Порядок уравнивания нивелирного хода на практике
2 Порядок уравнивания нивелирной сети на практике
1 Порядок уравнивания нивелирного хода на практике
Для нивелирного хода III класса дано:
и 
— измеренные превышения прямого и обратного ходов (
);
— длины секций;
и 
— отметки исх. пунктов.
1. Вычисляют среднее превышение по секциям. Знак берут по прямому ходу, а величину – как среднее арифметическое из абсолютных значений 
и 
:
2. Контроль вычислений: 
(в пределах ошибок округления). Знак 
— как у 
.
3. Находят расхождения между превышениями прямого и обратного ходов: 
(в мм).
4. Допустимые (предельные) расхождения: 
, 
— длины секций.
5. Вычисляют СКО среднего превышения на 1 км хода: 
6. Ошибка самой ошибки (характеризует точность получения величины 
): 
7. Вычисляют невязку: 
, где 
, 
8. Допустимая невязка: 
, где 
— длина всего хода, т. е. 
9. Делают вывод о качестве (т. е. точности) полевых измерений:
а) если 
;
б) 
(допуск по инструкции для III класса)
в) 
, то измеренные превышения по точности соответствуют III классу. В противном случае их перемеряют в поле (т. е. до непосредственного уравнивания – отыскания поправок – необходимо решить вопрос – нужно ли вообще уравнивать, или же измерения некачественные, и надо их переделать).
Если ход IV класса, то вывод делают лишь анализируя невязку (т. к. ход – в одном направлении, отсутствуют разности 
), а 
10. Вычисляют поправки: 
11. Контроль: 
12. Уравненные превышения: 
13. Контроль: 
14. Уравненные отметки: 
15. Контроль: 
16. Вычисление веса уравненных отметок: 
17. СКО уравненных отметок: 
18. Ошибка самой отметки: 
19. Оценка точности уравненных отметок: из всех 
выбирается самая большая 
— отметка в слабом месте (≈ в середине). Должно выполняться условие 
, где 
— предельная СКО положения точки по высоте в середине хода после уравнивания. 
, где 
— СКО положения по высоте конечной точки хода до уравнивания. 
, где 
— длина хода.
20. Если 
, то уравненные отметки соответствуют по точности III кл. (Для IV кл. 
можно взять 10 мм – по инструкции).
2 Порядок уравнивания нивелирной сети на практике
1. Определить число независимых полигонов: 
, контроль 
2. Достроить сеть до 
полигонов (с учетом меньшего числа измерений)
3. Пронумеровать полигоны и выбрать направление обхода
4. Вычислить 
в достроенных полигонах
5. Вычислить невязки полигонов 
с учетом направлений
6. Вычислить периметры полигонов 
7. Определить допустимость невязок:
— III класс
— IV класс
должно быть 
8. Составить нормальные уравнения коррелат в общем виде:
9. Вычислить коэффициенты при 
:
Квадратичные: 
Неквадратичные: 
, 
и т. д.
«0» — если нет общей стороны
10. Составить систему в численном виде: 
— в мм
11. Решив систему, найти 
12. Поправки в превышения:
для несмежной стороны: 
; 
для смежной: 
13. Контроль: 
14. Уравненные превышения: 
15. Контроль: 
16. Уравненные отметки с контролем: 
17. Оценка точности: 
— из уравнивания, где 
18. Определить соответствие классу нивелирования:
должно быть: 
для III кл;
для IV кл.
2-ой раздел Лекция 13
КРУПНОМАСШТАБНЫЕ ТОПОГРАФИЧЕСКИЕ СЪЁМКИ. АЭРОФОТОСЪЁМКА
1Виды и масштабы топографических съёмок.
Топографическая карта — построенное в картографической проекции, уменьшенное, обобщённое изображение земной поверхности, позволяющее определять как плановое, так и высотное положение точек.
Государственные топографические карты нашей страны издаются в масштабах 1:1 000 000 и крупнее.
Топографический план – картографическое изображение на плоскости в ОРТОГОНАЛЬНОЙ проекции в крупном масштабе ограниченного участка местности, в пределах которого КРИВИЗНА уровенной поверхности не учитывается.
При создании топографических карт применяется КОНФОРМНАЯ проекция Гаусса эллипсоида на плоскости. (Конформный – подобный). Основные свойства конформного изображения:
— бесконечно малый контур на эллипсоиде изображают подобным ему на плоскости;
— углы передаются на плоскость без искажения;
-масштаб изображения в каждой точке зависит только от её координат и не зависит от направления.
Перечисленные свойства наряду с простотой учёта искажений имеет принятая в 1928г в РОССИИ система плоских прямоугольных координат в проекции ГАУССА – КРЮГЕРА. Эту проекцию Гаусс предложил и обосновал в гг, а в 1912г Крюгер дал рабочие формулы для вычисления в этой проекции, поэтому её называют проекцией ГАУССА-КРЮГЕРА.
При использовании проекции Гаусса земной эллипсоид разделяется на зоны меридианами. Протяжённость зон по долготе для создания топографических карт в масштабах 1:10 000 и мельче принимают равной 6°, а для карт в масштабах 1: 5000 и 1:2000 она равна 3° (трёхградусная зона).
Топографические планы в масштабах 1: 1000 и 1: 500 всегда создаются в ортогональной проекции.
На небольших участках земной поверхности при создании топографических планов масштабов 1:5 000 и 1:2 000 может также применяться ортогональная проекция.
Высоты точек при создании топографических карт и планов определяются в абсолютной Балтийской системе высот 1977 года от нуля Кронштадтского футштока.
Топографические карты и планы создают при помощи топографических съёмок.
Съёмкой называют процесс геодезических измерений на местности, выполняемых для составления карт и планов.
Топографические съёмки на территории нашей страны выполняются в масштабах 1:25000, 1:10000, 1: 5000, 1:2000, 1:1000 , 1:500 и 1:200. Последние 5 масштабов являются крупномасштабными.
Различают следующие виды топографической съёмки:
-с использованием спутниковой геодезической аппаратуры (приёмники GPS);
— наземное и воздушное лазерное сканирование.
Основным методом государственного картографирования является аэрофототопографический.
С 1935 года наиболее широко применяемым, вследствие удобства работы, наличия контроля, наглядности и пр., являлась мензульная съемка. С течением времени она постепенно утратила своё значение, а в настоящее время потеряла свою актуальность в связи с появлением новых приборов.
В настоящее время МЕНЗУЛЬНАЯ съёмка применяется в редких случаях, когда другие виды съёмок технически невозможны. Как правило, её применяют для съёмки крупного масштаба застроенной территории.
Мензульная съемка выполняется на чертежных основах, изготовленных из прозрачных малодеформирующихся пластиков или из высококачественной чертежной бумаги, наклеенной на алюминий или авиационную фанеру.
Съемка рельефа и контуров производится с помощью мензулы и номограммных кипрегелей и других приборов, их заменяющих.
В настоящее время создана новая серия электронных кипрегелей.
Тахеометрическая съемка, дающая возможность получить рельефный и контурный планы, является рентабельной в случае применения ее в условиях короткого полевого периода или мало благоприятных для съемки климатических условий. Она чаще всего ставится при съемке узких и длинных полос (инженерно-изыскательские работы). Главным недостатком тахеометрической съемки является зарисовка рельефа и составление контурного плана камеральным путем, что в результате дает менее точный рельефный план, чем при мензульной съемке.
Тахеометрическая съемка может быть поставлена самостоятельно или в комбинировании с другими методами работ.
Во избежание промахов и пропусков в изображении рельефа и ситуации, тахеометрическая съемка должна быть поставлена так, чтобы, одновременно с полевыми работами была организована и камеральная обработка данных. Одним из основных результатов научно – технического прогресса в области топографо-геодезических работ является появление автоматизированных технологий сбора, обработки и интерпретации информации об объектах топографической съемки. В настоящее время с появлением персональных компьютеров работа с геодезическими данными упростилась.
Тахеометрическую съемку целесообразно выполнять электронными тахеометрами (ЭТ), позволяющими автоматически получать превышение и горизонтальные проложения.
Современные ЭТ представляют сочетание светодальномера, кодового теодолита, микроЭВМ, а также регистратора информации, необходимого для автоматической записи результатов измерений. Программное обеспечение ЭТ позволяет решать целый ряд типовых задач, а именно:
— угловые и линейно-угловые засечки;
— уравнивание измеренных величин на станции;
— оценку точности результатов измерений и др.
Электронный тахеометр устанавливают на станции, а на пикетах ставят специальную вешку с отражателем, при наведении на нее автоматически определяется расстояние, горизонтальный и вертикальный углы.
Микро ЭВМ тахеометра по результатам измерений вычисляет приращение координат и превышение с учетом всех поправок. Результаты измерений могут вводится в специальное запоминающее устройство (накопитель информации), из которого информация поступает на ЭВМ, и по специальной программе выполняется построение цифровой модели местности или топографического плана. Графическое изображение топографического плана может быть выполнено графопостроителем, соединённым с ЭВМ.
ГОРИЗОНТАЛЬНАЯ съёмка застроенных территорий в масштабах 1:2000-1:5000 выполняется самостоятельно или в сочетании с высотной съёмкой способами: полярным, створов, графоаналитическим, засечек, перпендикуляров.
Наземную топографическую съёмку следует производить в случаях,
когда применение аэрофототопографической съёмки экономически нецелесообразно или не обеспечивает требуемой точности составления планов.
Стереотопографический способ создания крупномасштабных планов применяют для открытых, незаселенных участков местности, а также для застроенных территорий с одноэтажной или многоэтажной рассредоточенной застройкой. Сущность стереотопографического способа заключается в создании контурной части плана на основе материалов аэрофотосъемки и в рисовке рельефа, выполняемого в камеральных условиях на универсальных стереофотограмметрических приборах.
Достоинство стереотопографического способа является автоматизация целого ряда сложных процессов с использованием ЭВМ.
Комбинированный способ создания планов применяют для заселенных участков местности, городских территорий и поселков с плотной многоэтажной застройкой. При комбинированном способе контурную часто плана создают на основе материалов аэрофотосъемки, а дешифрирование участка и рисовку рельефа выполняют на фотопланах, непосредственно на местности обычными способами. Таким образом, комбинированная съемка является сочетанием аэрофотосъемки с приемами наземной (мензульной) съемки.
Видео:8 класс, 24 урок, Основные понятия, связанные с квадратными уравнениямиСкачать
Классификация основных способов уравнивания
Способы уравнивания результатов измерений в геодезических построениях разделяют на два основных вида: строгие способы и нестрогие способы уравнивания.
К строгим способам уравнивания относятся коррелатный и параметрический способы. Следует отметить, что оба названных способа дают идентичные результаты. Эти способы позволяют полностью реализовать в той или иной схеме метод наименьших квадратов практически для любых по сложности построений.
В некоторых случаях при уравнивании геодезических построений сравнительно малой точности применяют упрощенные способы уравнивания, которые относят к нестрогим способам. Например, в любом полигонометрическом ходе число избыточных измерений всегда равно трем. Очевидно, что число избыточных измерений практически намного меньше необходимых. Это приводит к тому, что при уравнивании не будет достигаться заметного повышения точности. Для одиночных полигонометрических ходов и даже для систем полигонометрических ходов с одной или двумя узловыми точками можно рекомендовать способ раздельного уравнивания. В частности, способ раздельного уравнивания был рассмотрен выше при обработке разомкнутого или замкнутого теодолитного хода: сначала выполнялось уравнивание горизонтальных углов (дирекци- онных углов), а затем — уравнивание приращений координат (координат). В полигонометрических сетях малой точности, содержащих не более 3 — 4 узловых пунктов, используют способ эквивалентной замены. Если полигонометрическая или нивелирная сеть содержит большое число исходных пунктов, то наиболее эффективно применять способ последовательных приближений. Нивелирные сети, состоящие из полигонов, при пониженных требованиях точности уравнивают, как правило, способом полигонов В.В. Попова. О всех указанных здесь способах пойдет речь в последующих параграфах этой главы.
Видео:Коррелатный способ. Решение системы условных уравненийСкачать
Основные геометрические условия, возникающие в построениях
Если геодезические построения состоят только из необходимых исходных данных, то такое построение (сеть) называется свободным (свободной) и уравниванию не подлежит. При наличии избыточных измерений построение (сеть) называется несвободным (несвободной), и в нем (ней) может быть выполнено уравнивание при наличии невязок, определяемых выполнением тех или иных условий в геометрических связях.
При уравнивании геодезических построений необходимо правильно определить число и видт. н. условных уравнений. В связи с этим должны быть составлены только необходимые условия, не больше. В противном случае система уравнений не может быть разрешима. Меньшее же число условий вообще исключает решение задачи уравнивания, поскольку хотя бы одна из невязок будет ис- ключена из рассмотрения._
Далее приведем основные геометрические условия, которые могут определять вид того или иного условного уравнения связи в геодезическом построении.
134.1. Условие фигуры
В замкнутой фигуре, имеющей п вершин, сумма уравненных значений измеренных углов должна быть равна 180° (л ± 2), т. е.;
где знак «плюс» в круглых скобках — для внешних, знак «минус» — для внутренних углов; р’ — исправленные (уравненные) углы.
В этом случае условное уравнение поправок имеет вид:
где Р(. — измеренные углы.
Поскольку два последних слагаемых образуют т. н. угловую невязку W, т. е.
то выражение (14.14) можно представить в виде: 
Выражение (14.13) и является геометрическим соотношением (уравнением связи) для условия фигуры.
Если в той же замкнутой фигуре углы заменить разностями направлений (т. е. отсчетов по горизонтальному кругу теодолита), то получается условное уравнение поправок для измеренных направлений:
В формуле (14.17) точкой стояния является точка i.
134.2. Условие горизонта
Сумма уравненных значений неперекрывающихся углов, измеренных независимо (т. е. отдельно друг от друга) вокруг одной вершины (рис. 14.1), должна быть равна 360°, т. е.;
Рис. 14.1. Условие горизонта
Условное уравнение поправок горизонта имеет вид (14.16), где
для измеренных углов Р(.
Для измеренных направлений условие горизонта не возникает, поскольку в этом случае всегда сумма углов, вычисленных по разностям направлений, будет равна 360° (зависимые измерения). Если же в измеренные углы ввести поправки, то и для направлений может возникнуть условие горизонта. Поэтому условные уравнения поправок со свободным членом, равным нулю, необходимо включать в уравнивание.
134.3. Условие суммы углов
Рис. 14.2. Условие суммы углов
Для измеренных в одной вершине углов Р2, рз и Р4 (рис. 14.2) должно соблюдаться следующее геометрическое условие:
В этом случае условное уравнение поправок будет иметь вид:
где Wp — свободный член уравнения, определяемый суммой 
134.4. Условие дирекционных углов
Для решения геодезического построения (при определении координат его точек) необходимо знать исходный дирекционный угол одной из его сторон. Если же в сети известны дирекционные углы других сторон, то каждый из них образует одно условие. Например, если в сети (рис. 14.3) известны дирекционные углы оц, а2 и а3, то геометрическое условие дирекционных углов запишется в виде:
Рис. 14.3. Условие дирекционных углов
Условные уравнения поправок в этом случае определяются выражениями:
В выражениях (14.23) — (14.25) принимается во внимание, что все дирекционные углы были измерены (они могут быть и вычислены по значениям координат, имеющих известные погрешности), т. е. содержат погрешности и подлежат уравниванию. Чаще всего дирекционные углы принимают исходными, т. е. содержащими погрешности весьма малые (ничтожные) по сравнению с погрешностями измеренных углов. В этом случае выражения (14.25) запишутся в виде:
- (а0 — исходные дирекционные углы).
- 134.5. Условие сторон
Предположим, что в фигуре (рис. 14.4) измерены все углы р и стороны s, и s2. Между сторонами, из решения треугольников, существует следующее соотношение:
Это равенство можно представить в виде нелинейной функции
Приведем нелинейную функцию (14.30) к линейному виду, разложив ее в ряд Тейлора и ограничиваясь только первыми членами разложения. Получим:
Найдем частные производные:
где s2° — вычисленное по формуле (14.29) значение s2 по измеренным аргументам s,, р1( р3, Р4, Р5. С учетом (14.32)
Аналогично можно записать выражения для р3, р4 и р5:
Введем следующие обозначения: 
Умножим выражение (14.31) на 1 / s2° и подставим в него значения частных производных (14.32) — (14.34). Уравнение поправок будет иметь вид:
где Ws = 2 0 2 р —относительная погрешность стороны s; 8, = ctg(3,;
р — угловая мера радиана.
Если стороны Sj и s2являются базисами (исходными), то поправки для них будут равны нулю. В этом случае условное уравнение поправок исходных сторон (базисов) упрощается:
где Ws = 2 02 р; s02 — базис.
Рис. 14.4. Условие сторон
134.G. Условие полюса
Условие полюса возникает в такой фигуре (рис. 14.5), в которой можно образовать замкнутый ряд треугольников, начинающихся и заканчивающихся на одной и той же стороне (например, центральная система, геодезический четырехугольник, веер). Если эту сторону принять за исходную (базис), то из решения треугольников можно получить эту сторону вторично.
Например, для центральной системы рис. 14.5 можно записать,
что 
Условное уравнение поправок данного полюса с учетом введенных выше обозначений (14.37) имеет вид:
Рис. 14.5. Условие полюса
132.7. Условие координат
В геодезическом построении каждый избыточный исходный пункт обусловливает два условных уравнения координат — уравнения абсцисс (х) и уравнения ординат (у).
Предположим, что измерения выполнены в цепочке треугольников триангуляции (рис. 14.6), заканчивающейся на избыточном пункте 5. Наметим ходовую линию, проходящую через вершины промежуточных углов г),: 1 — 3 — 4 — 5. В этом случае координатные условные уравнения (абсцисс и ординат) будут иметь вид:
При решении треугольников триангуляции стороны и дирекци- онные углы определяют от исходных сторон s0 (базиса) и исходного дирекционного угла а0:
Рис. 14.6. Условие координат
Представим уравнения (14.41) через поправки в углы в линейной форме:
Свободными членами Wx и Wy в уравнениях (14.43) являются приближенные значения искомых функций (14.41), вычисленные по измеренным горизонтальным углам с использованием равенств
Из уравнений (14.41) найдем частные производные (коэффициенты условных уравнений поправок) и подставим их в уравнения
- (14.43) . При этом поправки углов выражаются в секундах, свободные члены — в дециметрах, а разности координат — в километрах. Получим условные уравнения поправок:
- — для координатх (при уравнивании углов):
— для координат у (при уравнивании углов):
Здесь хпиуп — координаты последнего пункта (для рис. 14.6 хп = х5, Уп = 7s) > x i и 7, — координаты текущего пункта i ходовой линии, проходящей через вершины промежуточных углов ц,; vp, и vyi — поправки связующих углов Р и у (угол у лежит против исходной стороны треугольника); v4f — поправки промежуточных углов rj (записываются со знаком «плюс» для левых по ходу углов, со знаком «минус» —для правых по ходу углов).
📺 Видео
Химия | Молекулярные и ионные уравненияСкачать
Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать
Повторяем решение уравнений. Полезно всем! Вебинар | МатематикаСкачать
Как решают уравнения в России и СШАСкачать
После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать
МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать
Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать
Решаем ВСЕ уравнения из сборника Ященко | Parta 2023 | Базовая математикаСкачать
Абсолютная и условная сходимостьСкачать
Математический анализ, 37 урок, Знакопеременные ряды. Абсолютная и условная сходимостиСкачать
Основы параметрической формы метода наименьших квадратов (МНК) на примере уравнивания опорных сетей.Скачать
Курс по ОДУ: Уравнения Клеро и Лагранжа | Занятие 8Скачать
СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать
19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать
Система уравнений Тема4 Системы уравнений, в которых оба уравнения второй и более высокой степени.Скачать
