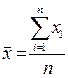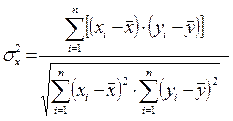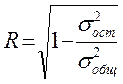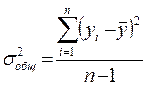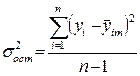Виды уравнений регрессии относительно формы зависимостей

Содержание статьи:

• Уравнение регрессии
• Линейное уравнение
• Нелинейное уравнение
• Виды регрессии
• Парная регрессия
• Множественная регрессия

Регрессия. Многие из нас слышали это слово, но немногие знают, что же это такое на самом деле. Попробуем разобраться. Регрессия — это зависимость между определёнными переменными, с помощью которой можно спрогнозировать будущее поведение данных переменных. Причём, под переменными подразумеваются всевозможные периодические явления вплоть до человеческого поведения.

Видео:Множественная регрессияСкачать

Уравнение регрессии

Зачастую, регрессия подаётся в виде простого уравнения, которое раскрывает зависимость и силу связи между двумя группами числовых переменных, одна из которых называется зависимой (эндогенной), а вторая — независимой (экзогенной или фактором). Если есть группа взаимосвязанных показателей, то зависимая переменная выбирается логическими размышлениями, а остальные выступают независимыми. То есть, если у нас есть расстояние между городами и затраты на путешествие, то вполне ясно, что затраты будут зависеть от расстояния. Уравнения бывают двух видов: линейные и нелинейные (это уже чистая математика). Стоит рассмотреть каждый из видов.

Видео:Парная регрессия: линейная зависимостьСкачать

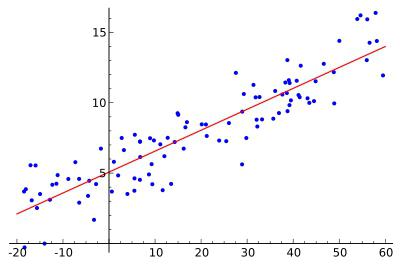
Линейное уравнение

Линейное уравнение иллюстрирует строго линейную связь между переменными, то есть в нём отсутствуют степени, дроби, тригонометрические функции. Решается стандартными математическими способами.

Видео:Математика #1 | Корреляция и регрессияСкачать

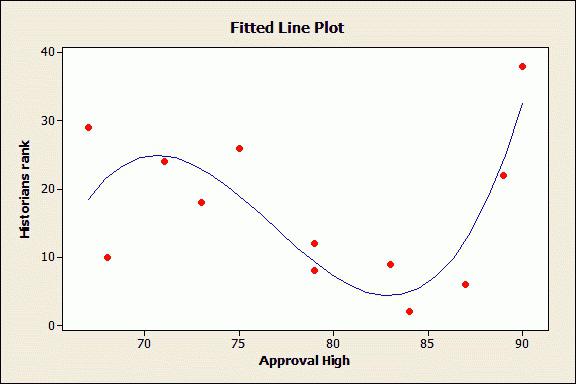
Нелинейное уравнение

Логично предположить, что в нелинейный класс уравнений входит всё то, что не вошло в линейный. Решаются такие уравнения сведением к линейному типу, а дальше – по накатанной дорожке.

Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Виды регрессии

Регрессия бывает двух видов: парная (линейная и нелинейная) и множественная (линейная и нелинейная). Разница между ними в виде уравнения и количестве независимых переменных. Логично, что парная регрессия — это когда одна зависимая переменная и одна независимая, в множественной — независимых переменных несколько. В природе имеет место исключительно множественная регрессия, так как нельзя ограничить внешнее влияние на какое-то явление строго одним фактором. Рассмотрим оба вида регрессий детальнее.

Видео:Что такое линейная регрессия? Душкин объяснитСкачать

Парная регрессия

Парная (её ещё называют двухфакторной) модель проста в использовании, так как у нас всего две переменные: эндогенная и экзогенная, а значит будет просто решить уравнение и провести анализ. А это значит, что и применять на практике такую модель очень легко.

Видео:Эконометрика. Множественная регрессия и корреляция.Скачать

Множественная регрессия

Множественная (многофакторная) модель намного сложнее, так как мы имеем уравнение с большим количеством переменных, для решения которого существуют определённые математические способы (метод наименьших квадратов например).

Итоги

Немного разобравшись в этой теме, приходишь к выводу, что регрессия очень необходимое понятие, помогающее предугадать поведение многих явлений. Его используют в экономике, психологии, химии, биологии, метеорологии и во многих других науках, причём существует множество программ, которые проводят все необходимые расчёты автоматически и сами выводят результаты и графики для анализа. Пользователю остаётся только считать результаты и правильно расшифровать их. А уж найти им применение вообще не проблема. Поэтому, я считаю, что необходимо иметь хотя бы малейшее понятие о том, что же такое эта пресловутая регрессия и где её использовать.

Видео про линейную регрессию и корреляцию:

Видео:Что такое регрессия и какие виды регрессии имеются? Душкин объяснитСкачать

Уравнение регрессии. Уравнение множественной регрессии

Во время учебы студенты очень часто сталкиваются с разнообразными уравнениями. Одно из них – уравнение регрессии — рассмотрено в данной статье. Такой тип уравнения применяется специально для описания характеристики связи между математическими параметрами. Данный вид равенств используют в статистике и эконометрике.

Видео:Множественная регрессия в ExcelСкачать

Определение понятия регрессии

В математике под регрессией подразумевается некая величина, описывающая зависимость среднего значения совокупности данных от значений другой величины. Уравнение регрессии показывает в качестве функции определенного признака среднее значение другого признака. Функция регрессии имеет вид простого уравнения у = х, в котором у выступает зависимой переменной, а х – независимой (признак-фактор). Фактически регрессия выражаться как у = f (x).

Видео:Линейная регрессияСкачать

Какие бывают типы связей между переменными

В общем, выделяется два противоположных типа взаимосвязи: корреляционная и регрессионная.

Первая характеризуется равноправностью условных переменных. В данном случае достоверно не известно, какая переменная зависит от другой.

Если же между переменными не наблюдается равноправности и в условиях сказано, какая переменная объясняющая, а какая – зависимая, то можно говорить о наличии связи второго типа. Для того чтобы построить уравнение линейной регрессии, необходимо будет выяснить, какой тип связи наблюдается.

Видео:Метод наименьших квадратов. Линейная аппроксимацияСкачать

Виды регрессий

На сегодняшний день выделяют 7 разнообразных видов регрессии: гиперболическая, линейная, множественная, нелинейная, парная, обратная, логарифмически линейная.

Видео:Множественная степенная регрессияСкачать

Гиперболическая, линейная и логарифмическая

Уравнение линейной регрессии применяют в статистике для четкого объяснения параметров уравнения. Оно выглядит как у = с+т*х+Е. Гиперболическое уравнение имеет вид правильной гиперболы у = с + т / х + Е. Логарифмически линейное уравнение выражает взаимосвязь с помощью логарифмической функции: In у = In с + т* In x + In E.

Видео:Линейная регрессия. Что спросят на собеседовании? ч.1Скачать

Множественная и нелинейная

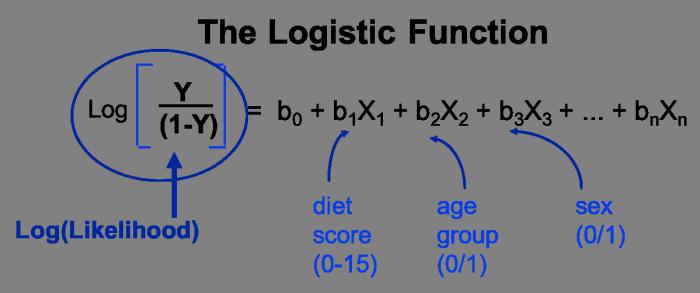
Два более сложных вида регрессии – это множественная и нелинейная. Уравнение множественной регрессии выражается функцией у = f(х₁ , х₂ . х_с)+E. В данной ситуации у выступает зависимой переменной, а х – объясняющей. Переменная Е — стохастическая, она включает влияние других факторов в уравнении. Нелинейное уравнение регрессии немного противоречиво. С одной стороны, относительно учтенных показателей оно не линейное, а с другой стороны, в роли оценки показателей оно линейное.

Видео:Практика Многофакторная регрессияСкачать

Обратные и парные виды регрессий

Обратная – это такой вид функции, который необходимо преобразовать в линейный вид. В самых традиционных прикладных программах она имеет вид функции у = 1/с + т*х+Е. Парное уравнение регрессии демонстрирует взаимосвязь между данными в качестве функции у = f (x) + Е. Точно так же, как и в других уравнениях, у зависит от х, а Е — стохастический параметр.

Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Понятие корреляции

Это показатель, демонстрирующий существование взаимосвязи двух явлений или процессов. Сила взаимосвязи выражается в качестве коэффициента корреляции. Его значение колеблется в рамках интервала [-1;+1]. Отрицательный показатель говорит о наличии обратной связи, положительный – о прямой. Если коэффициент принимает значение, равное 0, то взаимосвязи нет. Чем ближе значение к 1 – тем сильнее связь между параметрами, чем ближе к 0 – тем слабее.

Видео:Корреляция: коэффициенты Пирсона и Спирмена, линейная регрессияСкачать

Методы

Корреляционные параметрические методы могут оценить тесноту взаимосвязи. Их используют на базе оценки распределения для изучения параметров, подчиняющихся закону нормального распределения.

Параметры уравнения линейной регрессии необходимы для идентификации вида зависимости, функции регрессионного уравнения и оценивания показателей избранной формулы взаимосвязи. В качестве метода идентификации связи используется поле корреляции. Для этого все существующие данные необходимо изобразить графически. В прямоугольной двухмерной системе координат необходимо нанести все известные данные. Так образуется поле корреляции. Значение описывающего фактора отмечаются вдоль оси абсцисс, в то время как значения зависимого – вдоль оси ординат. Если между параметрами есть функциональная зависимость, они выстраиваются в форме линии.

В случае если коэффициент корреляции таких данных будет менее 30 %, можно говорить о практически полном отсутствии связи. Если он находится между 30 % и 70 %, то это говорит о наличии связей средней тесноты. 100 % показатель – свидетельство функциональной связи.

Нелинейное уравнение регрессии так же, как и линейное, необходимо дополнять индексом корреляции (R).

Видео:Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

Корреляция для множественной регрессии

Коэффициент детерминации является показателем квадрата множественной корреляции. Он говорит о тесноте взаимосвязи представленного комплекса показателей с исследуемым признаком. Он также может говорить о характере влияния параметров на результат. Уравнение множественной регрессии оценивают с помощью этого показателя.

Для того чтобы вычислить показатель множественной корреляции, необходимо рассчитать его индекс.

Видео:Что такое полиномиальная регрессия? Душкин объяснитСкачать

Метод наименьших квадратов

Данный метод является способом оценивания факторов регрессии. Его суть заключается в минимизировании суммы отклонений в квадрате, полученных вследствие зависимости фактора от функции.

Парное линейное уравнение регрессии можно оценить с помощью такого метода. Этот тип уравнений используют в случае обнаружения между показателями парной линейной зависимости.

Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Параметры уравнений

Каждый параметр функции линейной регрессии несет определенный смысл. Парное линейное уравнение регрессии содержит два параметра: с и т. Параметр т демонстрирует среднее изменение конечного показателя функции у, при условии уменьшения (увеличения) переменной х на одну условную единицу. Если переменная х – нулевая, то функция равняется параметру с. Если же переменная х не нулевая, то фактор с не несет в себе экономический смысл. Единственное влияние на функцию оказывает знак перед фактором с. Если там минус, то можно сказать о замедленном изменении результата по сравнению с фактором. Если там плюс, то это свидетельствует об ускоренном изменении результата.

Каждый параметр, изменяющий значение уравнения регрессии, можно выразить через уравнение. Например, фактор с имеет вид с = y – тх.

Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Сгруппированные данные

Бывают такие условия задачи, в которых вся информация группируется по признаку x, но при этом для определенной группы указываются соответствующие средние значения зависимого показателя. В таком случае средние значения характеризуют, каким образом изменяется показатель, зависящий от х. Таким образом, сгруппированная информация помогает найти уравнение регрессии. Ее используют в качестве анализа взаимосвязей. Однако у такого метода есть свои недостатки. К сожалению, средние показатели достаточно часто подвергаются внешним колебаниям. Данные колебания не являются отображением закономерности взаимосвязи, они всего лишь маскируют ее «шум». Средние показатели демонстрируют закономерности взаимосвязи намного хуже, чем уравнение линейной регрессии. Однако их можно применять в виде базы для поиска уравнения. Перемножая численность отдельной совокупности на соответствующую среднюю можно получить сумму у в пределах группы. Далее необходимо подбить все полученные суммы и найти конечный показатель у. Чуть сложнее производить расчеты с показателем суммы ху. В том случае если интервалы малы, можно условно взять показатель х для всех единиц (в пределах группы) одинаковым. Следует перемножить его с суммой у, чтобы узнать сумму произведений x на у. Далее все суммы подбиваются вместе и получается общая сумма ху.

Видео:Парная регрессия: гиперболическая зависимостьСкачать

Множественное парное уравнение регрессии: оценка важности связи

Как рассматривалось ранее, множественная регрессия имеет функцию вида у = f (x₁,x₂,…,x_m)+E. Чаще всего такое уравнение используют для решения проблемы спроса и предложения на товар, процентного дохода по выкупленным акциям, изучения причин и вида функции издержек производства. Ее также активно применяют в самых разнообразным макроэкономических исследованиях и расчетах, а вот на уровне микроэкономики такое уравнение применяют немного реже.

Основной задачей множественной регрессии является построение модели данных, содержащих огромное количество информации, для того чтобы в дальнейшем определить, какое влияние имеет каждый из факторов по отдельности и в их общей совокупности на показатель, который необходимо смоделировать, и его коэффициенты. Уравнение регрессии может принимать самые разнообразные значения. При этом для оценки взаимосвязи обычно используется два типа функций: линейная и нелинейная.

Линейная функция изображается в форме такой взаимосвязи: у = а₀ + a₁х₁ + а₂х₂,+ . + a_mx_m. При этом _а2, a_m, считаются коэффициентами «чистой» регрессии. Они необходимы для характеристики среднего изменения параметра у с изменением (уменьшением или увеличением) каждого соответствующего параметра х на одну единицу, с условием стабильного значения других показателей.

Нелинейные уравнения имеют, к примеру, вид степенной функции у=ах₁ b1 х₂ b2 . x_m bm . В данном случае показатели b₁, b₂. b_m – называются коэффициентами эластичности, они демонстрируют, каким образом изменится результат (на сколько %) при увеличении (уменьшении) соответствующего показателя х на 1 % и при стабильном показателе остальных факторов.

Какие факторы необходимо учитывать при построении множественной регрессии

Для того чтобы правильно построить множественную регрессию, необходимо выяснить, на какие именно факторы следует обратить особое внимание.

Необходимо иметь определенное понимание природы взаимосвязей между экономическими факторами и моделируемым. Факторы, которые необходимо будет включать, обязаны отвечать следующим признакам:

• Должны быть подвластны количественному измерению. Для того чтобы использовать фактор, описывающий качество предмета, в любом случае следует придать ему количественную форму.
• Не должна присутствовать интеркорреляция факторов, или функциональная взаимосвязь. Такие действия чаще всего приводят к необратимым последствиям – система обыкновенных уравнений становится не обусловленной, а это влечет за собой ее ненадежность и нечеткость оценок.
• В случае существования огромного показателя корреляции не существует способа для выяснения изолированного влияния факторов на окончательный результат показателя, следовательно, коэффициенты становятся неинтерпретируемыми.

Методы построения

Существует огромное количество методов и способов, объясняющих, каким образом можно выбрать факторы для уравнения. Однако все эти методы строятся на отборе коэффициентов с помощью показателя корреляции. Среди них выделяют:

• Способ исключения.
• Способ включения.
• Пошаговый анализ регрессии.

Первый метод подразумевает отсев всех коэффициентов из совокупного набора. Второй метод включает введение множества дополнительных факторов. Ну а третий – отсев факторов, которые были ранее применены для уравнения. Каждый из этих методов имеет право на существование. У них есть свои плюсы и минусы, но они все по-своему могут решить вопрос отсева ненужных показателей. Как правило, результаты, полученные каждым отдельным методом, достаточно близки.

Методы многомерного анализа

Такие способы определения факторов базируются на рассмотрении отдельных сочетаний взаимосвязанных признаков. Они включают в себя дискриминантный анализ, распознание обликов, способ главных компонент и анализ кластеров. Кроме того, существует также факторный анализ, однако он появился вследствие развития способа компонент. Все они применяются в определенных обстоятельствах, при наличии определенных условий и факторов.

Корреляционный анализ и регрессионный анализ.

Общие сведения

Статистической называется зависимость между случайными величинами, при которой изменение одной из величин влечет за собой изменение закона распределения другой величины.

Односторонняя вероятностная зависимость между случайными есть регрессия. Она устанавливает соответствие между этими величинами.

1.Регрессия относительно числа переменных:

— Простая регрессия – регрессия между двумя Множественная регрессия – это регрессия между зависимой переменной переменой у и несколькими объясняющими переменными х₁, х₂, …, х_n. Множественная линейная регрессия имеет следующий вид:

Где: у – функция регрессии;

а₀ — свободный член уравнения;

n – число факторов, включаемых в модель.

1. Регрессия относительно формы зависимости:

— линейная регрессия, выражаемая линейной функцией;

— нелинейная регрессия, выражаемая нелинейной функцией.

2. В зависимости от характера регрессии различают следующие ее виды:

— положительную регрессию. Она имеет место, если с увеличением (уменьшением) объясняющей переменной значения зависимой переменной также соответственно увеличиваются (уменьшаются);

— отрицательную регрессию. В этом случае с увеличением или уменьшением объясняющей переменной зависимая переменная уменьшается или увеличивается.

3. Относительно типа соединения явлений различают:

— непосредственную регрессию. В этом случае зависимая и объясняющая переменные связаны непосредственно друг с другом;

— косвенную регрессию. В этом случае объясняющая переменная действует на зависимую через ряд других переменных;

— ложную регрессию. Она возникает при формальном подходе к исследуемым явлениям без уяснения того, какие причины обуславливают данную связь.

Регрессия тесно связана с корреляцией.

Корреляция в широком смысле слова означает связь, соотношение между объективно существующими явлениями. Связи между явлениями могут быть различны по силе.

Понятия «корреляция» и «регрессия» тесно связаны между собой. В корреляционном анализе оценивается сила связи, а регрессионном анализе исследуется ее форма. Корреляция в широком смысле объединяет корреляцию в узком смысле и регрессию.

Корреляция, как и регрессия, имеет различные виды:

1. Относительно характера корреляции различают:

2. Относительно числа переменных –

3. Относительно формы связи –

4. Относительно типа соединения –

Исследование корреляционных связей называется корреляционным анализом, а исследование односторонних стохастических зависимостей – регрессионным анализом.

Линейная регрессия

Пусть задана система случайных величин Х и Y и случайные величины Х и Y зависимы.

Представим одну из случайных величин как линейную функцию другой случайной величины Х:

где a, b — параметры, которые подлежат определению.

Эти параметры могут быть определены различными способами, наиболее часто используется метод наименьших квадратов (МНК).

Функцию g(x) называют наилучшим приближением в смысле МНК, если математическое ожидание М[Y-g(x)] 2 принимает возможное наименьшее значение.

В этом случае функцию g(x) называют средней квадратической регрессией Y на X.

Рассмотрим определение параметров выбранного уравнения прямой линии средней квадратической регрессии по не сгруппированным данным. Пусть изучается система количественных признаков (Х ,Y), т.е. ведутся наблюдения за случайной двухмерной величиной (Х , Y). Пусть в результате n наблюдений получено n пар чисел (х₁,у₁), (х₂, у₂), …, (х_n, y_n).

Требуется по полученным данным найти выборочное уравнение прямой линии средней квадратической регрессии:

Поскольку данные несгруппированные, т.е. каждая пара чисел встречается один раз, то можно перейти от условной средней к переменной у. Угловой коэффициент k обозначим через k = p и назовем ее выборочной оценкой коэффициента регрессии .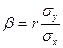

Итак, требуется найти:

Метод наименьших квадратов (МНК) получили систему двух линейных уравнений относительно p и b. Решая эту систему, получим:

;

.

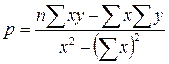
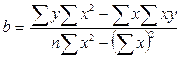
Основные понятия корреляционно-регрессионного анализа

1. Среднее значение переменной определяется по следующей формуле:

где х₁ – эмпирическое значение переменной х; n – число наблюдений.

2. Коэффициент корреляции

Коэффициент корреляции характеризует тесноту или силу связи между переменными у и х. Значения, переменные r_ху, заключены в пределах от –1 до +1. При положительном значении r_ху имеет место положительная корреляция, т.е. с увеличением (уменьшением) значений одной переменной (х) значение другой (у) соответственно увеличивается (уменьшается). При отрицательном значении r_ху имеет место отрицательная корреляция, т.е. с увеличением (уменьшением) значений х значения у соответственно уменьшаются (увеличиваются). При изучении экономического явления, зависящего от многих факторов, строится множественная регрессионная зависимость. В этом случае для характеристики тесноты связи используются коэффициент множественной корреляции:

где s 2 _ост – остаточная дисперсия зависимой переменной;

s 2 _общ – общая дисперсия зависимой переменной.

3. Общая дисперсия определяется по формуле:

Величина s 2 _общ характеризует разброс наблюдений фактических значений от среднего значения .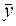

Остаточная дисперсия определяется по следующей формуле:

где у_iт – теоретические значения переменной у, полученные по уравнению регрессии при подстановке в него наблюдаемых фактических значений х_i.

Остаточная дисперсия характеризует ту часть рассеяния переменной у, которая возникает из-за всякого рода случайностей и влияния неучтенных факторов.

4. Коэффициент детерминации служит для оценки точности регрессии, т.е. соответствие полученного уравнения регрессии имеющимся эмпирическим данным, и вычисляется по формуле

Изменяется Д в пределах от 0 до 1, т.е.

Модель считается тем точнее, чем ближе Д к 1, т.е. чем меньше s 2 _ост.

Стандартная ошибка оценки равна .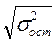

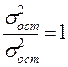
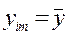
Если Д=0, это значит отношение , т.е. s 2 _ост = s 2 _общ, и, следовательно, . В этом случае прямая регрессии будет параллельна оси X, корреляционно-регрессионная связь между X и Y отсутствует. Если

Д = 1 , значит, , т.е. s 2 _ост = 0. Отсюда у_i = y_iT т. е наблюдаемые точки лежат на построенной прямой, следовательно, зависимость функциональная.

8. Корреляционное отношение используется для оценки тесно­ты связи между двумя явлениями, в частности для определения тесноты связи исходного ряда у_i, с теоретическим рядом y_iT . Корре­ляционное отношение определяют по данным, сгруппированным по объясняющей переменной по следующей формуле: