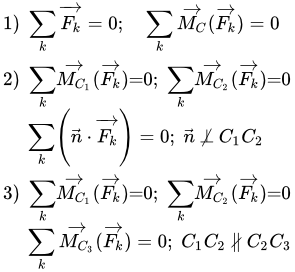Виды систем сил и их уравнения равновесия

Рассмотрим условия равновесия произвольной плоской и пространственной систем сил, включая три основные формы и частные случаи равновесия для систем параллельных и сходящихся сил:

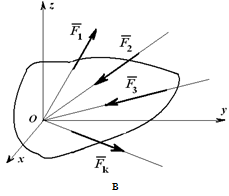
Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.

Если система уравновешена, то получаем условия равновесия: R=0, M_O=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:

Видео:§ 5.3. Уравнения равновесия плоской системы силСкачать

Формы условий равновесия

Первая форма

Для плоской системы сил (например, в плоскости Oxy) из этих уравнений получаются только три:

причем оси и точка O, относительно которой пишется уравнение моментов, выбираются произвольно. Это первая форма уравнений равновесия.

Вторая форма

Уравнения равновесия могут быть записаны иначе:

Это вторая форма уравнений равновесия, причем ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B.

Третья форма

Это третья форма уравнений равновесия, причем точки A, B и C не должны лежать на одной прямой.

Предпочтительность написания форм уравнений равновесия зависит от конкретных условий задачи и навыков решающего.

Видео:Урок 70. Виды равновесия. Условие равновесия тела при отсутствии вращения.Скачать

Другие условия равновесия

При действии на тело плоской системы параллельных сил одно из уравнений исчезает и остаются два уравнения (рисунок 1.26, а):

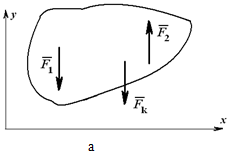
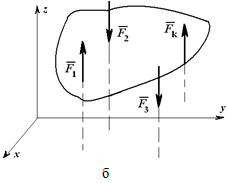
Для пространственной системы параллельных сил (рисунок 1.26, б) могут быть записаны три уравнения равновесия:

Для системы сходящихся сил (линии действия которых пересекаются в одной точке) можно написать три уравнения для пространственной системы:

и два уравнения для плоской системы:

В каждом из вышеприведенных случаев число неизвестных, находимых при решении уравнений, соответствует числу записанных уравнений равновесия.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Статика. Условия равновесия плоской системы сил (23)Скачать

Условия и уравнения равновесия твердого тела: плоской и пространственной системы сил

Видео:Система сходящихся силСкачать

Условия равновесия произвольной системы сил

Еще Ньютон говорил, что если геометрическая сумма сил, действующая на тело, равна нулю, то тело:

• либо находится в состоянии покоя;
• либо движется равномерно прямолинейно.

Из теоретической механики известно, что действие нескольких сил, просуммировав, можно заменить равнодействующей силой:

Тогда обязательное условие равновесия можно записать так:

Однако для полного равновесия, часто, этого условия недостаточно, если тело имеет возможность вращаться относительно какой-то точки или оси, то для равновесия такой системы, необходимо, чтобы выполнялось условие:

где M — главные момент системы, который эквивалентен сумме моментов системы относительно некоторого центра.

Видео:Статика. Момент сил. Условия равновесия тел | Физика ЕГЭ, ЦТ, ЦЭ | Физика для школьниковСкачать

Условия равновесия плоской системы сил

Выше описанные условия означают, что система будет находится в равновесии, когда все силы, действующие на систему, будут взаимно уравновешиваться и момент относительно любой произвольной точки будет равен нулю, отсюда вытекает первая и основная форма условий равновесия для плоской системы сил:

Вторая форма условий равновесия записывается следующим образом:

Важно! Ось не должна быть перпендикулярна прямой AB.

И, наконец, третья форма условий равновесия выглядит так:

Из данной системы уравнений следует, что для равновесия системы достаточно равенства нулю суммы моментов относительно трех точек.

Важно! Точки, относительно которых записываются уравнения не должны лежать на одной прямой.

Видео:§ 5.1. Уравнения равновесия произвольной системы силСкачать

Уравнения равновесия для плоской системы сил

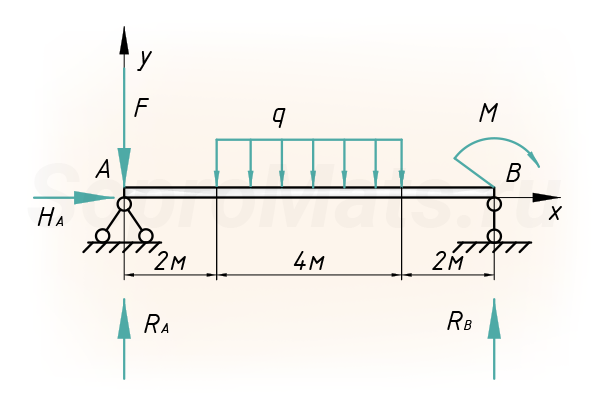
Рассмотрим на примере плоской балки, как записываются уравнения равновесия. Использовать будет классическую (первую) форму условия равновесия:

Сумма моментов относительно точки A:

Сумма проекций всех сил на вертикальную ось (y):

Сумма проекций всех сил на горизонтальную ось(x):

Видео:Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

Условие равновесия пространственной системы сил

Для пространственной системы сил условие равновесие выглядит вот так:

Таким образом, пространственная система будет находиться в равновесии, если суммы проекций сил на координатные оси, а также суммы моментов относительно осей будут равны нулю.

Видео:Определение реакций опор в балке. Сопромат.Скачать

Уравнения равновесия для пространственной системы сил

В качестве примера рассмотрим пространственную раму, закруженную сосредоточенными силами. Составим для нее шесть уравнений равновесия:

Видео:Встреча с Путиным в общежитии МГУ на Воробьевых горах!Скачать

Условия равновесия твердого тела и системы сил

Видео:Система сходящихся сил. Решение задач по МещерскомуСкачать

Термины «равновесие тела» и «равновесие системы сил»

Здесь мы рассматриваем условия, при которых твердое тело находится в состоянии равновесия. Под этим мы подразумеваем, что если тело в некоторый момент времени покоилось, то оно будет покоится и в последующие моменты времени, относительно некоторой инерциальной системы отсчета.

Об этом также говорят как об условиях равновесия системы сил. Под системой сил в статике всегда подразумеваются силы, действующие на абсолютно твердое тело, или на систему, которую, в соответствии с принципом затвердевания, можно считать единым твердым телом. Все законы преобразования сил относятся только к силам, действующим на одно тело. Под равновесием системы сил подразумевается уравновешенная система, которую эквивалентными преобразованиями можно свести к отсутствию сил, то есть к их взаимному уничтожению. Тогда если система сил находится в равновесии, то она эквивалентна отсутствию сил. Такая система не оказывает никакого влияния на движение тела. И если оно вначале покоилось, то будет покоиться и в последующие моменты времени.

Термин равновесие системы сил несколько отличается от термина равновесие твердого тела. Различие связано с тем, что силы, действующие на тело можно разбить на несколько систем. Некоторые из этих систем могут находиться в равновесии, и не оказывать влияния на движение. Их можно исключить. В тоже время могут существовать неравновесные системы, приводящие к изменению скорости движения центра масс и момента импульса тела.

Однако, если в систему сил включены все внешние силы, то эти понятия совпадают. Далее мы будем говорить об условиях равновесия твердого тела. Эти условия есть то же самое, что условия равновесия системы сил, если под системой сил подразумевать все внешние силы, действующие на тело.

Видео:Физика 10 класс (Урок№14 - Статика. Равновесие абсолютно твердых тел.)Скачать

Основная форма условий равновесия

Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма внешних сил, действующих на тело равнялась нулю, и чтобы векторная сумма моментов этих сил, относительно произвольно выбранного центра C , равнялась нулю:
(1.1) ;
(1.2) .
Доказательство ⇓

Здесь внешние силы приложены к телу в точках .

Если мы выберем прямоугольную систему координат Cxyz с центром в точке C , то условия (1.1) и (1.2) можно выразить через проекции сил и моментов на оси этой системы. Тогда мы получим шесть уравнений:
; ; ;
; ; .
Из этих уравнений можно определить шесть неизвестных величин, определяющих реакции опор тела.

Также мы можем произвольным образом выбрать три вектора, не лежащие в одной плоскости, и спроектировать уравнения (1.1) и (1.2) на их направления. В результате мы также получим систему из шести уравнений.

Видео:РЕАКЦИИ ИОННОГО ОБМЕНА, ИОННОЕ УРАВНЕНИЕ - Урок Химия 9 класс / Подготовка к ЕГЭ по ХимииСкачать

Вторая форма условий равновесия

Условия равновесия можно записать и в других формах, которые могут оказаться более удобными при решении некоторых задач. Вот вторая форма условий равновесия.

Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма моментов внешних сил, действующих на тело, относительно произвольным образом выбранных точек и равнялась нулю, и чтобы сумма проекций сил на произвольное направление, не перпендикулярное направлению , равнялась нулю:
(2.1) ;
(2.2) ;
(2.3) .
Доказательство ⇓

Если спроектировать условия (2.1) и (2.2) на оси координат, то получим три уравнения (2.1), три уравнения (2.2) и одно уравнение (2.3). Всего получается семь уравнений. Однако, как показано ниже, между шестью уравнениями (2.1) и (2.2) существует одна линейная зависимость (см. «Линейная зависимость моментов относительно двух точек ⇓»). Таким образом, в условиях (2.1-3) имеется 7-1=6 линейно независимых уравнений, из которых можно определить шесть неизвестных величин.

Видео:Статика. Система сил. Лекция (12)Скачать

Третья форма условий равновесия

И наконец, имеется третья форма условий равновесия.

Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма моментов внешних сил, действующих на тело, относительно произвольным образом выбранных точек и , не лежащих на одной прямой, равнялась нулю:
(3.1) ;
(3.2) ;
(3.3) ;
(3.4) .
Доказательство ⇓

Если спроектировать условия (3.1), (3.2) и (3.3) на оси координат, то получим три уравнения (3.1), три уравнения (3.2) и три уравнения (3.3) – всего девять уравнений. Как показано ниже, между шестью уравнениями (3.1) и (3.2) существует одна линейная зависимость (см. «Линейная зависимость моментов относительно двух точек ⇓»). Аналогичным образом, между шестью уравнениями (3.1) и (3.3) существует еще одна линейная зависимость. И наконец, между шестью уравнениями (3.2) и (3.3) существует третья линейная зависимость. То есть, в условиях (3.1-3) имеется три линейных зависимости. Тогда число линейно независимых уравнений равно 9–3=6. Также, как и в предыдущих формах, из этих уравнений можно определить шесть неизвестных величин.

Видео:Теоретическая механика. Нахождение реакций связей на при плоской системе сил. Задача 1, часть 1Скачать

Условия равновесия плоского тела

Теперь рассмотрим плоскую систему, в которой тело может совершать движение только вдоль одной плоскости. При этом силы также направлены в этой плоскости. В этом случае мы выбираем систему отсчета так, чтобы оси x и y лежали в рассматриваемой плоскости, а ось z была ей перпендикулярна. Тогда приведенные выше формы условий равновесия сохраняют свой вид. При этом z – компоненты всех сил равны нулю: , а у моментов сил отлична от нулю только z – компонента: .

Выпишем условия равновесия для плоской системы, расписав их по компонентам.

Основная форма условий равновесия
;
;
.

Вторая форма условий равновесия
;
;
.

Третья форма условий равновесия
;
;
;
.

Здесь во всех формах имеется по три уравнения, из которых можно определить три неизвестных величины.

Видео:Математика это не ИсламСкачать

Доказательство условий равновесия

Основная форма условий равновесия

Все формы ⇑ Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма внешних сил, действующих на тело равнялась нулю, и чтобы векторная сумма моментов этих сил, относительно произвольно выбранного центра C , равнялась нулю:
(1.1)
(1.2)

Для доказательства воспользуемся законами движения твердого тела. Они описываются уравнениями:
(1.3) ;
(1.4) .
Здесь – ускорение центра масс тела; M – его масса; – момент импульса тела относительно произвольно выбранного центра C ; – внешние силы, действующие на тело, приложенные в точках .

Пусть тело находится в состоянии покоя относительно выбранной инерциальной системы координат. Тогда, в этой системе координат, скорость всех точек равна нулю. Отсюда
, .
Подставляя в (1.3) и (1.4), получаем (1.1) и (1.2).
Необходимость доказана.

Пусть выполняются условия равновесия (1.1) и (1.2). Подставляя их в уравнения движения (1.3) и (1.4), получаем:
;
.
Отсюда получаем, что скорость движения центра масс и момент импульса постоянны, не меняются со временем. Пусть теперь в начальный момент времени тело покоилось. Тогда скорость движения его центра масс и момент импульса равны нулю. А поскольку они не меняются со временем, то они равны нулю и в последующие моменты времени. То есть тело остается в состоянии покоя во все моменты времени.

Вторая форма условий равновесия

Все формы ⇑ Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма моментов внешних сил, действующих на тело, относительно произвольным образом выбранных точек и равнялась нулю, и чтобы сумма проекций сил на произвольное направление, не перпендикулярное направлению , равнялась нулю:
(2.1)
(2.2)
(2.3)

Пусть тело находится в состоянии равновесия. Возьмем произвольные точки и и выберем произвольный вектор , не перпендикулярный прямой : . Как уже было доказано при выводе основной формы условий равновесия ⇑, выполняются условия (1.1) и(1.2):
(1.1) :
(1.2) .
Поскольку здесь C – произвольная точка, то в качестве нее возьмем точку . В результате получим (2.1):
(2.1) .
Далее, в качестве C возьмем точку . Получим (2.2):
(2.2) .
Теперь спроектируем уравнение (1.1) на направление вектора . Получим (2.3):
(2.3) .
Это уравнение выполняется для любых векторов . В том числе и для тех, направление которых не перпендикулярно : .
Необходимость доказана.

Пусть выполняются условия (2.1), (2.2) и (2.3). Докажем, что тогда тело будет находиться в состоянии равновесия. Воспользуемся векторным уравнением:
(2.4) .
Подставим его в (2.1):

.
Поскольку из (2.2), , то .
Отсюда
(2.5) ,
где λ – произвольная постоянная. Умножим это уравнение скалярно на и применим (2.3):
(2.6) .
По условию, . Поэтому .
Тогда, чтобы выполнялось (2.6) нужно положить . В результате из (2.5) получаем уравнение (1.1):
.
Условие (1.2) также выполняется, если положить . Таким образом мы получили, что если выполняются условия (2.1), (2.2) и (2.3), то выполняются условия (1.1) и (1.2):
(1.1) ;
(1.2) .
Как мы уже доказали при выводе основной формы условий равновесия ⇑, это означает, что тело находится в равновесии.

Линейная зависимость моментов относительно двух точек

Докажем, что уравнения (2.1) и (2.2) линейно зависимы. Для этого из (2.1) вычтем (2.2) и воспользуемся (2.4):

.
Здесь мы ввели обозначение . Умножим это уравнение скалярно на :
.
В правой части стоит смешанное произведение векторов, в которое входит два одинаковых вектора . Поэтому оно равно нулю. В результате получаем линейную зависимость между уравнениями (2.1) и (2.2):
.

Третья форма условий равновесия

Все формы ⇑ Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма моментов внешних сил, действующих на тело, относительно произвольным образом выбранных точек и , не лежащих на одной прямой, равнялась нулю:
(3.1) ;
(3.2) ;
(3.3) ;
(3.4) .

Пусть тело находится в состоянии равновесия. Как уже было доказано при выводе основной формы условий равновесия ⇑, при этом выполняется условие (1.2):
(1.2) .
Возьмем произвольные точки , и , не лежащие на одной прямой. Поскольку в (1.2) C – произвольная точка, то в качестве нее возьмем последовательно точки , и . В результате получим уравнения (3.1), (3.2) и (3.3):
(3.1) ;
(3.2) ;
(3.3) .
Эти уравнения выполняются для любых точек , и . В том числе и для тех, которые не лежат на одной прямой:
(3.4) .
Необходимость доказана.

Пусть выполняются условия (3.1), (3.2), (3.3) и (3.4). Докажем, что тело будет находиться в состоянии равновесия. Как и при доказательстве второй формы, воспользуемся векторным уравнением:
(3.5) .
Подставим его в (3.1):

.
Поскольку из (3.2), , то .
Отсюда
(3.6) ,
где – произвольная постоянная.

Выполняя те же действия с точками и , найдем:
(3.7) ,
где – также произвольная постоянная. Сравнивая (3.6) и (3.7) имеем:
(3.8) .
Поскольку векторы и не параллельны, то уравнение (3.8) может выполняться только при . Тогда из (3.6) следует, что .
Для доказательства того, что , достаточно умножить скалярно уравнение (3.8) на вектор, перпендикулярный и вектор, перпендикулярный .

Если обозначить точку как C , то (3.1) примет вид:
.

Итак, мы получили, что если выполняются условия (3.1), (3.2) и (3.3), то выполняются условия (1.1) и (1.2):
(1.1) ;
(1.2) .
Как мы уже доказали при выводе основной формы условий равновесия ⇑, это означает, что тело находится в равновесии.

Автор: Олег Одинцов . Опубликовано: 30-09-2019

🎦 Видео

Сперматозоид-чемпион | наглядно показано оплодотворениеСкачать

«Открытое интервью» с российским футурологом Сергеем ПереслегинымСкачать

Основные определения статикиСкачать

Комплексные соединения. 1 часть. 11 класс.Скачать

определение реакций в стержнях от действия грузовСкачать