Виды движения и их уравнения

теория по физике 🧲 кинематика

Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними.

Основная задача механики — определение положение тела в пространстве в любой момент времени.

Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение и его виды

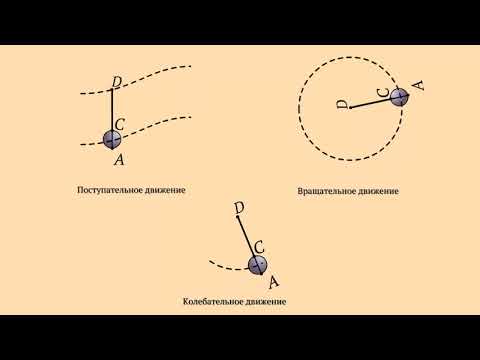
По характеру движения точек тела выделяют три вида механического движения:

• Поступательное. Это движение, при котором все точки тела движутся одинаково. Если через тело мысленно провести прямую, то после изменения положения этого тела в пространстве данная прямая останется параллельной самой себе.
• Вращательное. Это движение, при котором все точки тела движутся, описывая окружности.
• Колебательное. Это движение тела, которое повторяется точно или приблизительно через определенные интервалы времени. От вращательного движения его отличает то, что при колебаниях тело перемещается в двух взаимно противоположных направлениях.

По типу линии, вдоль которой движется тело, выделяют два вида движения:

• Прямолинейное — тело движется по прямой линии.
• Криволинейное — тело движется по кривой линии, в том числе замкнутой.

По скорости выделяют два вида движения:

• Равномерное — скорость движущегося тела остается неизменной.
• Неравномерное — скорость движущегося тела с течением времени меняется.

По ускорению выделяют три вида движения:

• Равноускоренное — тело движется неравномерно с постоянным ускорением (положительным). Скорость увеличивается.
• Равнозамедленное — тело движется неравномерно с постоянным замедлением (отрицательным ускорением). Скорость уменьшается.
• Ускоренное — тело движется неравномерно с меняющимся ускорением. Скорость может, как увеличиваться, так и уменьшаться.

Что нужно для описания механического движения?

Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.

Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.

Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.

Тело отсчета — тело, относительно которого рассматривается движение.

Часы — прибор для отсчета времени. Время измеряется в секундах (с).

При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.

Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.

Виды систем координат

В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:

• Одномерную. Используется, когда положение материальной точки можно задать только одной координатой x — M(x) . В этом случае тело движется прямолинейно.
• Двумерную. Используется, когда положение материальной точки можно задать двумя координатами x и y — M(x,y). Тело в этом случае движения по плоскости.
• Трехмерную. Используется, когда положение материальной точки можно задать тремя координатами x, y и z — M(x,y,z). Тело в этом случае изменяет положение в трехмерном пространстве.

Способы описания механического движения

Описать механическое движение можно двумя способами:

Координатный способ

Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:

Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.

Векторный способ

Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.

Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:

Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.

Характеристики механического движения

Движение материальной точки характеризуют три физические величины:

Перемещение

Перемещение (вектор перемещения) — направленный отрезок, начало которого совпадает с начальным положением точки, а конец — с его конечным положением. Обозначается как S .

Перемещение точки определяется как изменение радиус-вектора. Это изменение обозначается как Δ r . С точки зрения геометрии вектор перемещения равен разности радиус-векторов, задающих конечное и начальное положение точки:

Траектория — линия, которую описывает тело во время движения.

Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).

Путь есть функция времени:

Модуль перемещения — длина вектора перемещения. Обозначается как |Δ r |. Единица измерения — метры (м).

Модуль перемещения необязательно должен совпадать с длиной пути.

Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.

Путь равен длине окружности. Поэтому:

Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.

Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?

Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:

Скорость

Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.

В физике скорость обозначается V . Математически скорость определяется формулой:

Скорость характеризуется не только направлением вектора скорости, но и его модулем.

Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).

Математическое определение модуля скорости:

Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:

Ускорение

Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.

В физике ускорение обозначается a . Математически оно определяется формулой:

Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с 2 ).

Математическое определение модуля скорости:

v — скорость тела в данный момент времени, v₀— его скорость в начальный момент времени, t — время, в течение которого эта скорость менялась.

Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:

Проекция вектора перемещения на ось координат

Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.

Проекция вектора на ось OX:

Проекция вектора на ось OY:

Знаки проекций перемещения

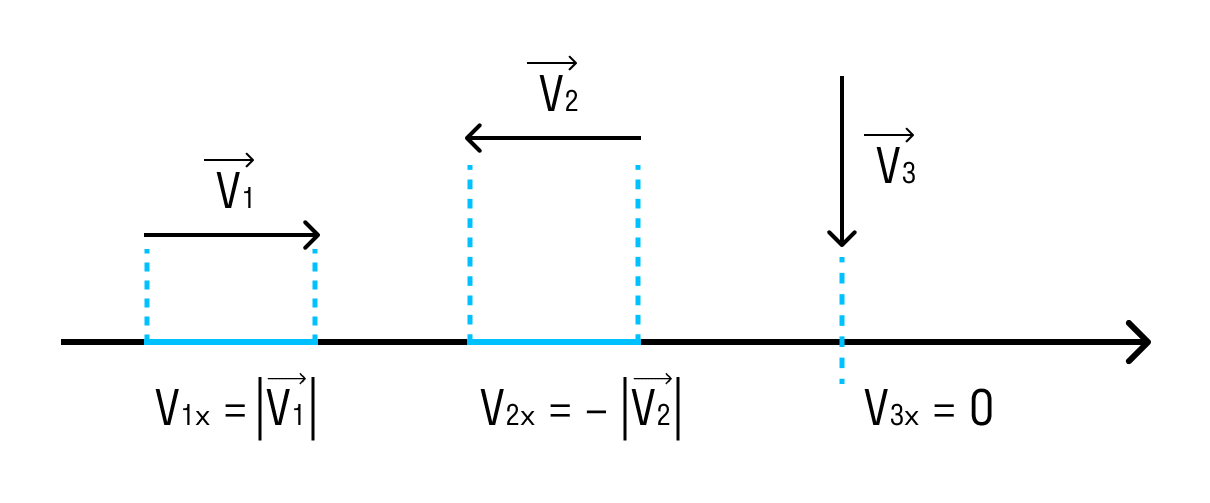
• Проекция является положительной, если движение от начала проекции вектора к проекции конца происходит сонаправленно оси координат.
• Проекция является отрицательной, если движение от начала проекции вектора к проекции конца направлено в сторону, противоположную направлению координатной оси.

Внимание!

Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.

Модуль перемещения — длина вектора перемещения:

Модуль перемещения измеряется в метрах (м).

Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:

Выразив проекции вектора перемещения через координаты, эта формула примет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:

Общий вид уравнений координат:

Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.

Определяем координаты начальной точки вектора:

Определяем координаты конечной точки вектора:

Проекция вектора перемещения на ось OX:

Проекция вектора перемещения на ось OY:

Применяем формулу для вычисления модуля вектора перемещения:

Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.

Извлекаем известные данные:

Для определения координаты точки В понадобятся формулы:

Выразим из них координаты конечного положения точки:

Точка В имеет координаты (5; 10).

Алгоритм решения

1. Записать исходные данные в определенной системе отсчета.
2. Записать формулу ускорения.
3. Выразить из формулы ускорения скорость.
4. Найти искомую величину.

Решение

Записываем исходные данные:

• Тело начинает двигаться из состояния покоя. Поэтому его начальная скорость v₀ = 0 м/с.
• Ускорение, с которым тело начинает движение, равно: a = 4 м/с 2 .
• Время движения согласно условию задачи равно: t = 2 c.

Записываем формулу ускорения:

Так как начальная скорость равна 0, эта формула принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Отсюда скорость равна:

Подставляем имеющиеся данные и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Видео:МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ: Равномерное движение и Прямолинейное Движение || Скорость — Физика 7 классСкачать

Механическое движение

О чем эта статья:

Видео:Физика. Курс механики | Виды движения. Равномерное движениеСкачать

Механическое движение

Когда мы идем в школу или на работу, автобус подъезжает к остановке или сладкий корги гуляет с хозяином, мы имеем дело с механическим движением.

Механическим движением называется изменение положения тел в пространстве относительно других тел с течением времени.

«Относительно других тел» — очень важные слова в этом определении. Для описания движения нам нужны:

• тело отсчета
• система координат
• часы

В совокупности эти три параметра образуют систему отсчета.

В механике есть такой раздел — кинематика. Он отвечает на вопрос, как движется тело. Дальше мы с помощью кинематики опишем разные виды механического движения. Не переключайтесь 😉

Прямолинейное равномерное движение

Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.

Например, если у вас ограничение скорости на дороге 60 км/ч, и у вас нет никаких препятствий на пути — скорее всего, вы будете двигаться прямолинейно равномерно.

Мы можем охарактеризовать это движение следующими величинами.

Скалярные величины (определяются только значением)

• Время — в международной системе единиц СИ измеряется в секундах [с].
• Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].

Векторные величины (определяются значением и направлением)

• Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
• Перемещение — вектор, проведенный из начальной точки пути в конечную [м].

Видео:Физика - уравнения равноускоренного движенияСкачать

Проецирование векторов

Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.

Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.

Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.

Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики.

Скорость — это векторная физическая величина, которая характеризует быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.

Скорость

— скорость [м/с]
— перемещение [м]
— время [с]

Средняя путевая скорость

V ср.путевая = S/t

V ср.путевая — средняя путевая скорость [м/с]
S — путь [м]
t — время [с]

Задача

Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.

Решение:

Возьмем формулу средней путевой скорости
V ср.путевая = S/t

Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч

Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч

Уроки физики в онлайн-школе Skysmart не менее увлекательны, чем наши статьи!

Видео:Урок 7. Механическое движение. Основные определения кинематики.Скачать

Уравнение движения

Одной из основных задач механики является определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).

Уравнение движения

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_x — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v

Уравнение движения при движении против оси

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_x — скорость тела в данный момент времени [м/с]
t — момент времени [с]

Видео:Основные понятия и уравнения кинематики равноускоренного движения тела.Скачать

Прямолинейное равноускоренное движение

Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.

СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение — килограмм с приставкой «кило».

Итак, равноускоренное прямолинейное движение — это движение с ускорением по прямой линии. Движение, при котором скорость тела меняется на равную величину за равные промежутки времени.

Уравнение движения и формула конечной скорости

Основная задача механики не поменялась по ходу текста — определение положения тела относительно других тел в данный момент времени. У равноускоренного движения в уравнении появляется ускорение.

Уравнение движения для равноускоренного движения

x(t) — искомая координата в момент времени t [м]
x₀ — начальная координата [м]
v_0x — начальная скорость тела в [м/с]
t — время [с]
a_x — ускорение [м/с 2 ]

Для этого процесса также важно уметь находить конечную скорость — решать задачки так проще. Конечная скорость находится по формуле:

Формула конечной скорости

— конечная скорость тела [м/с]
— начальная скорость тела [м/с]
— время [с]
— ускорение [м/с 2 ]

Задача

Найдите местоположение автобуса, который разогнался до скорости 60 км/ч за 3 минуты, через 0,5 часа после начала движения из начала координат.

Решение:

Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:

Так как автобус двигался с места, . Значит

Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.

3 минуты = 3/60 часа = 1/20 часа = 0,05 часа

Подставим значения:
a = v/t = 60/0,05 = 1200 км/ч 2
Теперь возьмем уравнение движения.
x(t) = x₀ + v_0xt + a_xt 2 /2

Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:

Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.

Подставим циферки:
км

Ответ: через полчаса координата автобуса будет равна 150 км.

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Движение по вертикали

Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с 2 , а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).

Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с 2 . В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с 2 .

Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.

Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.

Видео:Виды механического движенияСкачать

Кинематика

Механика — это раздел физики, изучающий механическое движение тел.

Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.

Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если

• расстояние, которое проходит тело, много больше его размера;
• расстояние от данного тела до другого тела много больше его размера;
• тело движется поступательно.

Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.

Важно!
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.

Основная задача механики — определить положение тела в пространстве в любой момент времени.

Видео:Уравнение движенияСкачать

Механическое движение и его виды

Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение может быть:
1. по характеру движения

• поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
• вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
• колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;

2. по виду траектории

• прямолинейным — это движение, траектория которого прямая линия;
• криволинейным — это движение, траектория которого кривая линия;

• равномерным — движение, при котором скорость тела с течением времени не изменяется;
• неравномерным — это движение, при котором скорость тела с течением времени изменяется;

• равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
• равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.

Видео:Кинематика. Равномерное и равноускоренное движение. Урок 1Скачать

Относительность механического движения

Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.

Правило сложения перемещений

Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:

где ​ ( S ) ​ — перемещение тела относительно неподвижной системы отсчета;
​ ( S_1 ) ​ — перемещение тела относительно подвижной системы отсчета;
​ ( S_2 ) ​ — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.

Правило сложения скоростей

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:

где ​ ( v ) ​ — скорость тела относительно неподвижной системы отсчета;
​ ( v_1 ) ​ — скорость тела относительно подвижной системы отсчета;
​ ( v_2 ) ​ — скорость подвижной системы отсчета относительно неподвижной системы отсчета.

Относительная скорость

Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.

Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_ ) :

Определим скорость второго тела относительно первого ( v_ ) :

Следует помнить, что траектория движения тела и пройденный путь тоже относительны.

Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:

Если скорости направлены под углом ​ ( alpha ) ​ друг к другу, то относительная скорость рассчитывается по теореме косинусов:

Видео:Интенсив РЭ Максвелла для 7-8 классов | Блоки и как с ними работатьСкачать

Скорость

Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.

Обозначение — ​ ( v ) ​, единицы измерения — ​м/с (км/ч)​.

Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:

Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:

Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.

Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.

Видео:Равномерное прямолинейное движение - физика 9Скачать

Ускорение

Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.

Обозначение — ​ ( a ) ​, единица измерения — м/с 2 .
В векторном виде:

где ​ ( v ) ​ – конечная скорость; ​ ( v_0 ) ​ – начальная скорость;
​ ( t ) ​ – промежуток времени, за который произошло изменение скорости.

В проекциях на ось ОХ:

где ​ ( a_n ) ​ – нормальное ускорение, ​ ( a_ ) ​ – тангенциальное ускорение.

Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.

Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_ ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_ ) = 0, ( a_n ) = 0, ​ ( v ) ​ ≠ 0, то тело движется равномерно по прямой;
если ( a_ ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_ ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_ ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.

Видео:Урок 12. Равномерное прямолинейное движениеСкачать

Равномерное движение

Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

График скорости (проекции скорости)

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ​ ( t ) ​, тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ​ ( t ) ​, тело движется против оси ОХ.

Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)

График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ) , тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ) , тело движется против оси ОХ.

По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ) . Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ​ ( x=x(t) ) ​.

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Прямолинейное равноускоренное движение

Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:

При движении с ускорением скорость может как увеличиваться, так и уменьшаться.

Скорость тела при равноускоренном движении рассчитывается по формуле:

При разгоне (в проекциях на ось ОХ):

При торможении (в проекциях на ось ОХ):

График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:

График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ​ ( a_x ) ​ > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) ( v_ ) ​ > 0, ​ ( a_x ) ​ > 0.

График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_ ) > 0, ( a_x ) ( v_ ) ( a_x ) ( t_2-t_1 ) ​. Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Перемещение при равноускоренном движении рассчитывается по формулам:

Перемещение в ​ ( n ) ​-ую секунду при равноускоренном движении рассчитывается по формуле:

Координата тела при равноускоренном движении рассчитывается по формуле:

Видео:Поступательное и вращательное движенияСкачать

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Обозначение – ​ ( g ) ​, единицы измерения – м/с 2 .

Важно! ( g ) = 9,8 м/с 2 , но при решении задач считается, что ( g ) = 10 м/с 2 .

Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

Если тело падает вниз без начальной скорости, то ​ ( v_0 ) ​ = 0.
Время падения рассчитывается по формуле:

Тело брошено вверх:

Если брошенное вверх тело достигло максимальной высоты, то ​ ( v ) ​ = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали со скоростью ​ ( v_0=v_ ) ​;
2. равноускоренного движения по вертикали с ускорением свободного падения ​ ( g ) ​ и без начальной скорости ​ ( v_=0 ) ​.

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали;
2. равноускоренного движения по вертикали с ускорением свободного падения.

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ​ ( v_0 ) ​, с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ​ ( alpha ) ​, под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Видео:Прямолинейное движение. 10 класс.Скачать

Движение по окружности с постоянной по модулю скоростью

Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.

Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ​ ( a_ ) ​, единицы измерения – ​м/с 2​ .

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ​ ( T ) ​, единицы измерения – с.

где ​ ( N ) ​ – количество оборотов, ​ ( t ) ​ – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ​ ( nu ) ​, единицы измерения – с –1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ​ ( v ) ​, единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ​ ( omega ) ​, единицы измерения – рад/с .

Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:

Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:

Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ​ ( v_1 ) ​, и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ) , то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки ​ ( (m) ) ​ равна нулю, мгновенная скорость в верхней точке ​ ( (n) ) ​ равна удвоенной скорости ​ ( v_1 ) ​, мгновенная скорость точки ​ ( (p) ) ​, лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ​ ( (c) ) ​ – по теореме косинусов.

🔥 Видео

Механическое движение и его характеристики. 7 класс.Скачать

Различные виды механического движенияСкачать

Кинематика за 8 минСкачать

Виды движенияСкачать

Движение точки тела. Способы описания движения | Физика 10 класс #2 | ИнфоурокСкачать