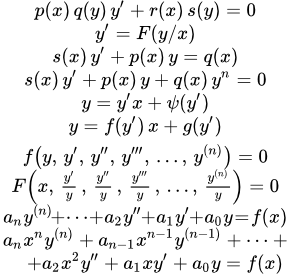Виды дифференциальных уравнений и методы их решения таблица

Далее в тексте – функции своих аргументов. Штрих ′ означает производную по аргументу. – постоянные.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Дифференциальные уравнения первого порядка

Особенности дифференциальных уравнений первого порядка

При решении уравнений первого порядка функцию y и переменную x следует считать равноправными. То есть решение может быть в виде так и в виде .

Дифференциальные уравнения первого порядка, разрешенные относительно производной

Уравнения с разделяющимися переменными

;
. Подробнее
Приводящиеся к уравнениям с разделяющимися переменными:
Подробнее

Однородные уравнения

Однородные уравнения не меняют свой вид при замене
,
где t – постоянная. При такой замене производная не меняется:
.
В общем виде обобщенно однородные уравнения можно записать посредством однородных функций:
,
где и – однородные функции с равными показателями однородности, то есть обладающие следующим свойством:
.
Общий вид однородных уравнений также можно выразить через произвольную функцию:
. Подробнее

Приводящиеся к однородным
,
где и – однородные функции с равными показателями однородности. В общем виде такие уравнения можно выразить через произвольную функцию:
. Подробнее

Обобщенно однородные уравнения не меняют свой вид при замене
,
где t – постоянная, . Для производной такая замена выглядит так:
.
В общем виде обобщенно однородные уравнения можно записать посредством однородных функций:
,
где и – однородные функции с равными показателями однородности.
Обобщенно однородные уравнения также можно записать через произвольную функцию:
. Подробнее

Линейные дифференциальные уравнения и приводящиеся к ним

• Линейное по y:
• Линейное по f(y):
• Линейное по x:
• Линейное по f(x):

Уравнения Риккати

Уравнения Якоби

Уравнения в полных дифференциалах

Интегрирующий множитель

Если дифференциальное уравнение первого порядка не приводится ни к одному из перечисленных типов, то следует попытаться найти интегрирующий множитель, чтобы свести его к уравнению в полных дифференциалах:
;
. Подробнее

Уравнения, не разрешенные относительно производной y′

Уравнения, допускающие решение относительно производной y′

Сначала нужно попытаться разрешить уравнение относительно производной y′ . Если это возможно, то уравнение может быть приведено к одному из перечисленных выше типов.

Уравнения, не разрешенные относительно производной y′

Уравнения, допускающие разложение на множители:
.
Подробнее
Уравнения, не содержащие x и y:
. Подробнее
Уравнения, не содержащие x или y:
, или . Подробнее

Уравнения, разрешенные относительно зависимой переменной y

Уравнения Клеро:
. Подробнее
Уравнения Лагранжа:
. Подробнее
Уравнения, приводящиеся к уравнению Бернулли:
;
. Подробнее

Видео:Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Дифференциальные уравнения высших порядков

Дифференциальные уравнения высших порядков, решаемые в квадратурах

Уравнения, содержащие переменную и старшую производную

Общий случай:
. Подробнее
Разрешенные относительно старшей производной:
. Подробнее
Разрешенные относительно переменной:
. Подробнее

Уравнения, содержащие только производные порядков n и n-1

Общий случай:
. Подробнее
Разрешенные относительно младшей производной:
. Подробнее
Разрешенные относительно старшей производной:
. Подробнее

Уравнения, содержащие только производные порядков n и n-2

Общий случай:
. Подробнее
Разрешенные относительно старшей производной:
. Подробнее

Дифференциальные уравнения, допускающие понижение порядка

Уравнения, не содержащие зависимую переменную y (и возможно несколько первых производных):
, или
. Подробнее
Уравнения, не содержащие независимую переменную x:
. Подробнее
Уравнения, однородные относительно функции и ее производных y, y′, y′′, . :
, причем
. Подробнее
Обобщенно однородные уравнения относительно переменных x, y:
, причем
. Подробнее
Дифференциальные уравнения с полной производной:
. Подробнее

Линейные дифференциальные уравнения с постоянными коэффициентами и приводящиеся к ним

Линейные однородные уравнения с постоянными коэффициентами:
. Подробнее
Линейные неоднородные уравнения с постоянными коэффициентами:
.
Решение методом Бернулли (двух функций)
Решение методом Лагранжа (вариация постоянных)
Решение линейной подстановкой
Линейные неоднородные уравнения со специальной неоднородной частью:
,
где – многочлены степеней и . Подробнее
Уравнения Эйлера:
. Подробнее

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 12-05-2012 Изменено: 26-11-2021

Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Виды дифференциальных уравнений

Существует целый ряд задач, в которых установить прямую связь между величинами, применяемыми для описания процесса, не получается. Единственное, что можно сделать, это получить равенство, запись которого включает производные исследуемых функций, и решить его. Решение дифференциального уравнения позволяет установить непосредственную связь между величинами.

В этом разделе мы займемся разбором решений дифференциальных уравнений, неизвестная функция в которых является функцией одной переменной. Мы построили теоретическую часть таким образом, чтобы даже человек с нулевым представлением о дифференциальных уравнениях мог без труда получить необходимые знания и справиться с приведенными задачами.

Если какие-то термины окажутся для вас новыми, обратитесь к разделу «Определения и понятия теории дифференциальных уравнений». А тем временем перейдем к рассмотрению вопроса о видах дифференциальных уравнений.

Для каждого из видов дифференциальных уравнений применяется свой метод решения. В этом разделе мы рассмотрим все эти методы, приведем примеры с подробными разборами решения. После ознакомления с темой вам необходимо будет определять вид дифференциального уравнения и выбирать наиболее подходящий из методов решения поставленной задачи.

Возможно, прежде чем приступить к решению дифференциальных уравнений, вам придется освежить в памяти такие темы как «Методы интегрирования» и «Неопределенные интегралы».

Начнем ознакомление с темой мы с видов обыкновенных дифференциальных уравнений 1 -го порядка. Эти уравнения могут быть разрешены относительно производной. Затем перейдем в ОДУ 2 -го и высших порядков. Также мы уделим внимание системам дифференциальных уравнений.

Напомним, что y ‘ = d x d y , если y является функцией аргумента x .

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Дифференциальные уравнения первого порядка

Простейшие дифференциальные уравнения первого порядка вида y ‘ = f ( x )

Начнем с примеров таких уравнений.

y ‘ = 0 , y ‘ = x + e x — 1 , y ‘ = 2 x x 2 — 7 3

Оптимальным для решения дифференциальных уравнений f ( x ) · y ‘ = g ( x ) является метод деления обеих частей на f ( x ) . Решение относительно производной позволяет нам прийти к уравнению вида y ‘ = g ( x ) f ( x ) . Оно является эквивалентом исходного уравнения при f ( x ) ≠ 0 .

Приведем примеры подобных дифференциальных уравнений:

e x · y ‘ = 2 x + 1 , ( x + 2 ) · y ‘ = 1

Мы можем получить ряд дополнительных решений в тех случаях, когда существуют значения аргумента х , при которых функции f ( x ) и g ( x ) одновременно обращаются в 0 . В качестве дополнительного решения в уравнениях f ( x ) · y ‘ = g ( x ) при заданных значениях аргумента может выступать любая функция, определенная для заданного значения х .

Наличие дополнительных решений возможно для дифференциальных уравнений x · y ‘ = sin x , ( x 2 — x ) · y ‘ = ln ( 2 x 2 — 1 )

Ознакомиться с теоретической частью и примерами решения задач таких уравнений вы можете в разделе «Простейшие дифференциальные уравнения 1 -го порядка».

Дифференциальные уравнения с разделяющимися переменными вида f 1 ( y ) · g 1 ( x ) d y = f 2 ( y ) · g 2 ( x ) d x или f 1 ( y ) · g 1 ( x ) · y ‘ = f 2 ( y ) · g 2 ( x )

Поговорим теперь об уравнениях с разделенными переменными, которые имеют вид f ( y ) d y = g ( x ) d x . Как следует из названия, к данному виду дифференциальных уравнений относятся выражения, которые содержат переменные х и у , разделенные знаком равенства. Переменные находятся в разных частях уравнения, по обе стороны от знака равенства.

Решить уравнения с разделенными переменными можно путем интегрирования обеих его частей: ∫ f ( y ) d y = ∫ f ( x ) d x

К числу дифференциальных уравнений с разделенными переменными можно отнести следующие из них:

y 2 3 d y = sin x d x , e y d y = ( x + sin 2 x ) d x

Для того, чтобы прийти от ДУ с разделяющимися переменными к ДУ с разделенными переменными, необходимо разделить обе части уравнения на произведение f 2 ( y ) ⋅ g 1 ( x ) . Так мы придем к уравнению f 1 ( y ) f 2 ( y ) d y = g 2 ( x ) g 1 ( x ) d x . Преобразование можно будет считать эквивалентным в том случае, если одновременно f 2 ( y ) ≠ 0 и g 1 ( x ) ≠ 0 . Если хоть одно из условий не будет соблюдаться, мы можем потерять часть решений.

В качестве примеров дифференциальных уравнений с разделяющимися переменными можно привести следующие из них: d y d x = y · ( x 2 + e x ) , ( y 2 + a r c cos y ) · sin x · y ‘ = cos x y .

К уравнениям с разделяющимися переменными мы можем прийти от ряда дифференциальных уравнений других видов путем замены переменных. Например, мы можем подставить в исходное уравнение z = a x + b y . Это позволит нам перейти к дифференциальному уравнению с разделяющимися переменными от дифференциального уравнения вида y ‘ = f ( a x + b y ) , a , b ∈ R .

Подставив z = 2 x + 3 y в уравнение y ‘ = 1 e 2 x + 3 y получаем d z d x = 3 + 2 e z e z .

Заменив z = x y или z = y x в выражениях y ‘ = f x y или y ‘ = f y x , мы переходим к уравнениям с разделяющимися переменными.

Если произвести замену z = y x в исходном уравнении y ‘ = y x · ln y x + 1 , получаем x · d z d x = z · ln z .

В ряде случаев прежде, чем производить замену, необходимо произвести преобразования исходного уравнения.

Предположим, что в условии задачи нам дано уравнение y ‘ = y 2 — x 2 2 x y . Нам необходимо привести его к виду y ‘ = f x y или y ‘ = f y x . Для этого нам нужно разделить числитель и знаменатель правой части исходного выражения на x 2 или y 2 .

Нам дано уравнение y ‘ = f a 1 x + b 1 y + c 1 a 2 x + b 2 y + c 2 , a 1 , b 1 , c 1 , a 2 , b 2 , c 2 ∈ R .

Для того, чтобы привести исходное уравнение к виду y ‘ = f x y или y ‘ = f y x , нам необходимо ввести новые переменные u = x — x 1 v = y — y 1 , где ( x 1 ; y 1 ) является решением системы уравнений a 1 x + b 1 y + c 1 = 0 a 2 x + b 2 y + c 2 = 0

Введение новых переменных u = x — 1 v = y — 2 в исходное уравнение y ‘ = 5 x — y — 3 3 x + 2 y — 7 позволяет нам получить уравнение вида d v d u = 5 u — v 3 u + 2 v .

Теперь выполним деление числителя и знаменателя правой части уравнения на u . Также примем, что z = u v . Получаем дифференциальное уравнение с разделяющимися переменными u · d z d u = 5 — 4 z — 2 z 2 3 + 2 z .

Подробный разбор теории и алгоритмов решения задач мы привели в разделе «Дифференциальные уравнения с разделяющимися переменными».

Линейные неоднородные дифференциальные уравнения первого порядка y ‘ + P ( x ) · y = Q ( x )

Приведем примеры таких уравнений.

К числу линейных неоднородных дифференциальных уравнений 1 -го порядка относятся:

y ‘ — 2 x y 1 + x 2 = 1 + x 2 ; y ‘ — x y = — ( 1 + x ) e — x

Для решения уравнений этого вида применяется метод вариации произвольной постоянной. Также мы можем представить искомую функцию у в виде произведения y ( x ) = u ( x ) v ( x ) . Алгоритмы применения обоих методов мы привели в разделе «Линейные неоднородные дифференциальные уравнения первого порядка».

Дифференциальное уравнение Бернулли y ‘ + P ( x ) y = Q ( x ) y a

Приведем примеры подобных уравнений.

К числу дифференциальных уравнений Бернулли можно отнести:

y ‘ + x y = ( 1 + x ) e — x y 2 3 ; y ‘ + y x 2 + 1 = a r c t g x x 2 + 1 · y 2

Для решения уравнений этого вида можно применить метод подстановки z = y 1 — a , которая выполняется для того, чтобы свести исходное уравнение к линейному дифференциальному уравнению 1 -го порядка. Также применим метод представления функции у в качестве y ( x ) = u ( x ) v ( x ) .

Алгоритм применения обоих методов приведен в разделе «Дифференциальное уравнение Бернулли». Там же можно найти подробный разбор решения примеров по теме.

Уравнения в полных дифференциалах P ( x , y ) d x + Q ( x , y ) d y = 0

Если для любых значений x и y выполняется ∂ P ( x , y ) ∂ y = ∂ Q ( x , y ) ∂ x , то этого условия необходимо и достаточно, чтобы выражение P ( x , y ) d x + Q ( x , y ) d y представляло собой полный дифференциал некоторой функции U ( x , y ) = 0 , то есть, d U ( x , y ) = P ( x , y ) d x + Q ( x , y ) d y . Таким образом, задача сводится к восстановлению функции U ( x , y ) = 0 по ее полному дифференциалу.

Выражение, расположенное в левой части записи уравнения ( x 2 — y 2 ) d x — 2 x y d y = 0 представляет собой полный дифференциал функции x 3 3 — x y 2 + C = 0

Для более подробного ознакомления с теорией и алгоритмами решения примеров можно обратиться к разделу «Уравнения в полных дифференциалах».

Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать

Дифференциальные уравнения второго порядка

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = 0 , p , q ∈ R

Линейное однородное дифференциальное уравнение с постоянными коэффициентами обычно решается достаточно просто. Нам необходимо найти корни характеристического уравнения k 2 + p k + q = 0 . Здесь возможны три варианта в зависимости от различных p и q :

• действительные и различающиеся корни характеристического уравнения k 1 ≠ k 2 , k 1 , k 2 ∈ R ;
• действительные и совпадающие k 1 = k 2 = k , k ∈ R ;
• комплексно сопряженные k 1 = α + i · β , k 2 = α — i · β .

Значения корней характеристического уравнения определяет, как будет записано общее решение дифференциального уравнения. Возможные варианты:

• y = C 1 e k 1 x + C 2 e k 2 x ;
• y = C 1 e k x + C 2 x e k x ;
• y = e a · x · ( C 1 cos β x + C 2 sin β x ) .

Пример 13

Предположим, что у нас есть линейное однородное дифференциальное уравнение 2 -го порядка с постоянными коэффициентами y ‘ ‘ + 3 y ‘ = 0 . Найдем корни характеристического уравнения k 2 + 3 k = 0 . Это действительные и различные k 1 = — 3 и k 2 = 0 . Это значит, что общее решение исходного уравнения будет иметь вид:

y = C 1 e k 1 x + C 2 e k 2 x ⇔ y = C 1 e — 3 x + C 2 e 0 x ⇔ y = C 1 e — 3 x + C 2

Восполнить пробелы в теоретической части и посмотреть подробный разбор примеров по теме можно в статье «Линейные однородные дифференциальные уравнения 2 -го порядка с постоянными коэффициентами».

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = f ( x ) , p , q ∈ R

Основным способом решение уравнений данного вида является нахождение суммы общего решения y 0 , которое соответствует линейному однородному дифференциальному уравнению y ‘ ‘ + p y ‘ + q y = 0 , и частного решения y

исходного уравнения. Получаем: y = y 0 + y

Способ нахождения y 0 мы рассмотрели в предыдущем пункте. Найти частное решение y

мы можем методом неопределенных коэффициентов при определенном виде функции f ( x ) , которая расположена в правой части записи исходного выражения. Также применим метод вариации произвольных постоянных.

К числу линейных неоднородных дифференциальных уравнений 2 -го порядка с постоянными коэффициентами относятся:

y ‘ ‘ — 2 y ‘ = ( x 2 + 1 ) e x ; y ‘ ‘ + 36 y = 24 sin ( 6 x ) — 12 cos ( 6 x ) + 36 e 6 x

Теоретические выкладки и подробный разбор примеров по теме можно найти в разделе «ЛНДУ 2 -го порядка с постоянными коэффициентами».

Линейные однородные дифференциальные уравнения (ЛОДУ) y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x )

Линейные однородные и неоднородные дифференциальные уравнения и постоянными коэффициентами являются частными случаями дифференциальных уравнений этого вида.

На некотором отрезке [ a ; b ] общее решение линейного однородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 представлено линейной комбинацией двух линейно независимых частных решений y 1 и y 2 этого уравнения, то есть, y = C 1 y 1 + C 2 y 2 .

Частные решения мы можем выбрать из систем независимых функций:

1 ) 1 , x , x 2 , . . . , x n 2 ) e k 1 x , e k 2 x , . . . , e k n x 3 ) e k 1 x , x · e k 1 x , . . . , x n 1 · e k 1 x , e k 2 x , x · e k 2 x , . . . , x n 2 · e k 2 x , . . . e k p x , x · e k p x , . . . , x n p · e k p x 4 ) 1 , c h x , s h x

Однако существуют примеру уравнений, для которых частные решения не могут быть представлены в таком виде.

Возьмем для примера линейное однородное дифференциальное уравнение x y ‘ ‘ — x y ‘ + y = 0 .

Общее решение линейного неоднородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x ) мы можем найти в виде суммы y = y 0 + y

, где y 0 — общее решение соответствующего ЛОДУ, а y

частное решение исходного дифференциального уравнения. Найти y 0 можно описанным выше способом. Определить y

нам поможет метод вариации произвольных постоянных.

Возьмем для примера линейное неоднородное дифференциальное уравнение x y ‘ ‘ — x y ‘ + y = x 2 + 1 .

Более подробно этот раздел освещен на странице «Линейные дифференциальные уравнения второго порядка».

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Дифференциальные уравнения высших порядков

Дифференциальные уравнения, допускающие понижение порядка

Мы можем провести замену y ( k ) = p ( x ) для того, чтобы понизить порядок исходного дифференциального уравнения F ( x , y ( k ) , y ( k + 1 ) , . . . , y ( n ) ) = 0 , которое не содержит искомой функции и ее производных до k — 1 порядка.

В этом случае y ( k + 1 ) = p ‘ ( x ) , y ( k + 2 ) = p ‘ ‘ ( x ) , . . . , y ( n ) = p ( n — k ) ( x ) , и исходное дифференциальное уравнение сведется к F 1 ( x , p , p ‘ , . . . , p ( n — k ) ) = 0 . После нахождения его решения p ( x ) останется вернуться к замене y ( k ) = p ( x ) и определить неизвестную функцию y .

Дифференциальное уравнение y ‘ ‘ ‘ x ln ( x ) = y ‘ ‘ после замены y ‘ ‘ = p ( x ) станет уравнением с разделяющимися переменными y ‘ ‘ = p ( x ) , и его порядок с третьего понизится до первого.

В уравнении, которое не содержит аргумента х и имеет вид F ( y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) = 0 , порядок может быть заменен на единицу следующим образом: необходимо провести замену d y d x = p ( y ) , где p ( y ( x ) ) будет сложной функцией. Применив правило дифференцирования, получаем:

d 2 y d x 2 = d p d y d y d x = d p d y p ( y ) d 3 y d x 3 = d d p d y p ( y ) d x = d 2 p d y 2 d y d x p ( y ) + d p d y d p d y d y d x = = d 2 p d y 2 p 2 ( y ) + d p d y 2 p ( y )
Полученный результаты подставляем в исходное выражение. При этом мы получим дифференциальное уравнение, порядок которого на единицу меньше, чем у исходного.

Рассмотрим решение уравнения 4 y 3 y ‘ ‘ = y 4 — 1 . Путем замены d y d x = p ( y ) приведем исходное выражение к уравнению с разделяющимися переменными 4 y 3 p d p d y = y 4 — 1 .

Более подробно решения задач по теме рассмотрены в разделе «Дифференциальные уравнения, допускающие понижение порядка».

Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 и y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x )

Решение уравнений данного вида предполагает выполнение следующих простых шагов:

• находим корни характеристического уравнения k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 ;
• записываем общее решение ЛОДУ y 0 в стандартной форме, а общее решение ЛНДУ представляем суммой y = y 0 + y

— частное решение неоднородного дифференциального уравнения.

Нахождение корней характеристического уравнения подробно описано в разделе «Решение уравнений высших степеней». Для нахождения y

целесообразно использовать метод вариации произвольных постоянных.

Линейному неоднородному ДУ с постоянными коэффициентами y ( 4 ) + y ( 3 ) — 5 y ‘ ‘ + y ‘ — 6 y = x cos x + sin x соответствует линейное однородное ДУ y ( 4 ) + y ( 3 ) — 5 y ‘ ‘ + y ‘ — 6 y = 0 .

Более детальный разбор теории и примеров по теме вы можете найти на странице « Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами».

Линейные однородные и неоднородные дифференциальные уравнения высших порядков y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 и y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x )

Найти решение ЛНДУ высших порядков можно благодаря сумме y = y 0 + y

, где y 0 — общее решение соответствующего ЛОДУ, а y

— частное решение неоднородного дифференциального уравнения.

y 0 представляет собой линейную комбинацию линейно независимых функций y 1 , y 2 , . . . , y n , каждая из которых является частным решением ЛОДУ, то есть, обращает равенство y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 в тождество. Частные решения y 1 , y 2 , . . . , y n обычно подбираются из известных систем линейно независимых функций. Подобрать их далеко не всегда просто и возможно, в этом и заключается основная проблема.

После того, как мы найдем общее решение ЛОДУ, найти частное решение соответствующего ЛНДУ можно благодаря методу вариации произвольных постоянных. Итак, y = y 0 + y

Получить более подробную информацию по теме можно в разделе «Дифференциальные уравнения высших порядков».

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Системы дифференциальных уравнений вида d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2

Данная тема подробно разобрана на странице «Системы дифференциальных уравнений». Там же приведены примеры задач с подробных разбором.

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Методические рекомендации для преподавателей математики и студентов средних специальных учебных заведений по теме «Дифференциальные уравнения»

Разделы: Математика

I. Обыкновенные дифференциальные уравнения

1.1. Основные понятия и определения

Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную x, искомую функцию y и её производные или дифференциалы.

Символически дифференциальное уравнение записывается так:

Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.

Решением дифференциального уравнения называется такая функция , которая обращает это уравнение в тождество.

Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение

1. Рассмотрим дифференциальное уравнение первого порядка

Решением этого уравнения является функция y = 5 ln x. Действительно, , подставляя y’ в уравнение, получим – тождество.

А это и значит, что функция y = 5 ln x– есть решение этого дифференциального уравнения.

2. Рассмотрим дифференциальное уравнение второго порядка y» — 5y’ +6y = 0. Функция – решение этого уравнения.

Действительно, .

Подставляя эти выражения в уравнение, получим: , – тождество.

А это и значит, что функция – есть решение этого дифференциального уравнения.

Интегрированием дифференциальных уравнений называется процесс нахождения решений дифференциальных уравнений.

Общим решением дифференциального уравнения называется функция вида ,в которую входит столько независимых произвольных постоянных, каков порядок уравнения.

Частным решением дифференциального уравнения называется решение, полученное из общего решения при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находится при определённых начальных значениях аргумента и функции.

График частного решения дифференциального уравнения называется интегральной кривой.

1.Найти частное решение дифференциального уравнения первого порядка

xdx + ydy = 0, если y = 4 при x = 3.

Решение. Интегрируя обе части уравнения, получим

Замечание. Произвольную постоянную С, полученную в результате интегрирования, можно представлять в любой форме, удобной для дальнейших преобразований. В данном случае, с учётом канонического уравнения окружности произвольную постоянную С удобно представить в виде .

— общее решение дифференциального уравнения.

Частное решение уравнения, удовлетворяющее начальным условиям y = 4 при x = 3 находится из общего подстановкой начальных условий в общее решение: 3 2 + 4 2 = C 2 ; C=5.

Подставляя С=5 в общее решение, получим x 2 +y 2 = 5 2 .

Это есть частное решение дифференциального уравнения, полученное из общего решения при заданных начальных условиях.

2. Найти общее решение дифференциального уравнения

Решением этого уравнения является всякая функция вида , где С – произвольная постоянная. Действительно, подставляя в уравнения , получим: , .

Следовательно, данное дифференциальное уравнение имеет бесконечное множество решений, так как при различных значениях постоянной С равенство определяет различные решения уравнения .

Например, непосредственной подстановкой можно убедиться, что функции являются решениями уравнения .

Задача, в которой требуется найти частное решение уравнения y’ = f(x,y) удовлетворяющее начальному условию y(x₀) = y₀, называется задачей Коши.

Решение уравнения y’ = f(x,y), удовлетворяющее начальному условию, y(x₀) = y₀, называется решением задачи Коши.

Решение задачи Коши имеет простой геометрический смысл. Действительно, согласно данным определениям, решить задачу Коши y’ = f(x,y) при условии y(x₀) = y₀,, означает найти интегральную кривую уравнения y’ = f(x,y) которая проходит через заданную точку M₀(x₀,y₀).

II. Дифференциальные уравнения первого порядка

2.1. Основные понятия

Дифференциальным уравнением первого порядка называется уравнение вида F(x,y,y’) = 0.

В дифференциальное уравнение первого порядка входит первая производная и не входят производные более высокого порядка.

Уравнение y’ = f(x,y) называется уравнением первого порядка, разрешённым относительно производной.

Общим решением дифференциального уравнения первого порядка называется функция вида , которая содержит одну произвольную постоянную.

Пример. Рассмотрим дифференциальное уравнение первого порядка .

Решением этого уравнения является функция .

Действительно, заменив в данном уравнении, его значением, получим

то есть 3x=3x

Следовательно, функция является общим решением уравнения при любом постоянном С.

Найти частное решение данного уравнения, удовлетворяющее начальному условию y(1)=1 Подставляя начальные условия x = 1, y =1 в общее решение уравнения , получим откуда C = 0.

Таким образом, частное решение получим из общего подставив в это уравнение, полученное значение C = 0 – частное решение.

2.2. Дифференциальные уравнения с разделяющимися переменными

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида: y’=f(x)g(y) или через дифференциалы , где f(x) и g(y)– заданные функции.

Для тех y, для которых , уравнение y’=f(x)g(y) равносильно уравнению, в котором переменная y присутствует лишь в левой части, а переменная x- лишь в правой части. Говорят, «в уравнении y’=f(x)g(y разделим переменные».

Уравнение вида называется уравнением с разделёнными переменными.

Проинтегрировав обе части уравнения по x, получим G(y) = F(x) + C– общее решение уравнения, где G(y) и F(x) – некоторые первообразные соответственно функций и f(x), C произвольная постоянная.

Алгоритм решения дифференциального уравнения первого порядка с разделяющимися переменными

1. Производную функции переписать через её дифференциалы
2. Разделить переменные.
3. Проинтегрировать обе части равенства, найти общее решение.
4. Если заданы начальные условия, найти частное решение.

Решить уравнение y’ = xy

Решение. Производную функции y’ заменим на

разделим переменные

проинтегрируем обе части равенства:

Ответ:

Найти частное решение уравнения

Это—уравнение с разделенными переменными. Представим его в дифференциалах. Для этого перепишем данное уравнение в виде Отсюда

Интегрируя обе части последнего равенства, найдем

Подставив начальные значения x₀ = 1, y₀ = 3 найдем С 9=1-1+C, т.е. С = 9.

Следовательно, искомый частный интеграл будет или

Составить уравнение кривой, проходящей через точку M(2;-3) и имеющей касательную с угловым коэффициентом

Решение. Согласно условию

Это уравнение с разделяющимися переменными. Разделив переменные, получим:

Проинтегрировав обе части уравнения, получим:

Используя начальные условия, x = 2 и y = — 3 найдем C:

Следовательно, искомое уравнение имеет вид

2.3. Линейные дифференциальные уравнения первого порядка

Линейным дифференциальным уравнением первого порядка называется уравнение вида y’ = f(x)y + g(x)

где f(x) и g(x) — некоторые заданные функции.

Если g(x)=0 то линейное дифференциальное уравнение называется однородным и имеет вид: y’ = f(x)y

Если то уравнение y’ = f(x)y + g(x) называется неоднородным.

Общее решение линейного однородного дифференциального уравнения y’ = f(x)y задается формулой: где С – произвольная постоянная.

В частности, если С =0, то решением является y = 0 Если линейное однородное уравнение имеет вид y’ = ky где k — некоторая постоянная, то его общее решение имеет вид: .

Общее решение линейного неоднородного дифференциального уравнения y’ = f(x)y + g(x) задается формулой ,

т.е. равно сумме общего решения соответствующего линейного однородного уравнения и частного решения данного уравнения.

Для линейного неоднородного уравнения вида y’ = kx + b,

где k и b— некоторые числа и частным решением будет являться постоянная функция . Поэтому общее решение имеет вид .

Пример. Решить уравнение y’ + 2y +3 = 0

Решение. Представим уравнение в виде y’ = -2y — 3 где k = -2, b= -3 Общее решение задается формулой .

Следовательно, где С – произвольная постоянная.

Ответ:

2.4. Решение линейных дифференциальных уравнений первого порядка методом Бернулли

Нахождение общего решения линейного дифференциального уравнения первого порядка y’ = f(x)y + g(x) сводится к решению двух дифференциальных уравнений с разделенными переменными с помощью подстановки y=uv, где u и v — неизвестные функции от x. Этот метод решения называется методом Бернулли.

Алгоритм решения линейного дифференциального уравнения первого порядка

1. Ввести подстановку y=uv.

2. Продифференцировать это равенство y’ = u’v + uv’

3. Подставить y и y’ в данное уравнение: u’v + uv’ = f(x)uv + g(x) или u’v + uv’ + f(x)uv = g(x).

4. Сгруппировать члены уравнения так, чтобы u вынести за скобки:

5. Из скобки, приравняв ее к нулю, найти функцию

Это уравнение с разделяющимися переменными:

Разделим переменные и получим:

Откуда . .

6. Подставить полученное значение v в уравнение (из п.4):

и найти функцию Это уравнение с разделяющимися переменными:

7. Записать общее решение в виде: , т.е. .

Найти частное решение уравнения y’ = -2y +3 = 0 если y =1 при x = 0

Решение. Решим его с помощью подстановки y=uv, .y’ = u’v + uv’

Подставляя y и y’ в данное уравнение, получим

Сгруппировав второе и третье слагаемое левой части уравнения, вынесем общий множитель u за скобки

Выражение в скобках приравниваем к нулю и, решив полученное уравнение, найдем функцию v = v(x)

Получили уравнение с разделенными переменными. Проинтегрируем обе части этого уравнения: Найдем функцию v:

Подставим полученное значение v в уравнение Получим:

Это уравнение с разделенными переменными. Проинтегрируем обе части уравнения: Найдем функцию u = u(x,c) Найдем общее решение: Найдем частное решение уравнения, удовлетворяющее начальным условиям y = 1 при x = 0:

Ответ:

III. Дифференциальные уравнения высших порядков

3.1. Основные понятия и определения

Дифференциальным уравнением второго порядка называется уравнение, содержащее производные не выше второго порядка. В общем случае дифференциальное уравнение второго порядка записывается в виде: F(x,y,y’,y») = 0

Общим решением дифференциального уравнения второго порядка называется функция вида , в которую входят две произвольные постоянные C₁ и C₂.

Частным решением дифференциального уравнения второго порядка называется решение, полученное из общего при некоторых значениях произвольных постоянных C₁ и C₂.

3.2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида y» + py’ +qy = 0, где pи q— постоянные величины.

Алгоритм решения однородных дифференциальных уравнений второго порядка с постоянными коэффициентами

1. Записать дифференциальное уравнение в виде: y» + py’ +qy = 0.

2. Составить его характеристическое уравнение, обозначив y» через r 2 , y’ через r, yчерез 1: r 2 + pr +q = 0

3.Вычислить дискриминант D = p 2 -4q и найти корни характеристического уравнения; при этом если:

а) D > 0; следовательно, характеристическое уравнение имеет два различных действительных корня . Общее решение дифференциального уравнения выражается в виде , где C₁ и C₂ — произвольные постоянные.

б) D = 0; следовательно, характеристическое уравнение имеет равные действительные корни . Общее решение дифференциального уравнения выражается в виде

Общее решение

Дифференцируя общее решение, получим

Составим систему из двух уравнений

Подставим вместо ,и заданные начальные условия:

Таким образом, искомым частным решением является функция

.

2. Найти частное решение уравнения

1.

1.

2. а)

2. а)

б)

б)

в)

в)

г)

г)

💡 Видео

Поле направлений дифференциального уравнения первого порядкаСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

Частное решение дифференциального уравнения. 11 класс.Скачать

2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Определяем тип ДУ 1Скачать