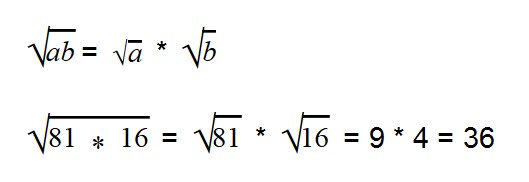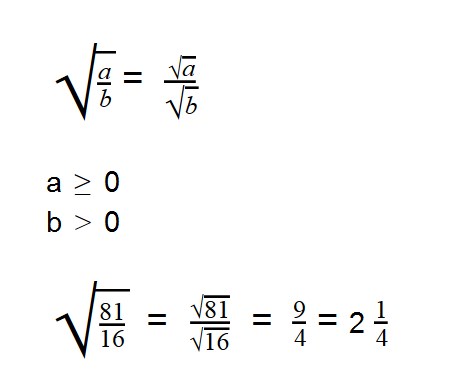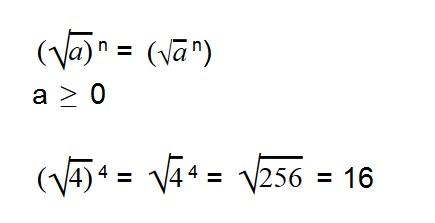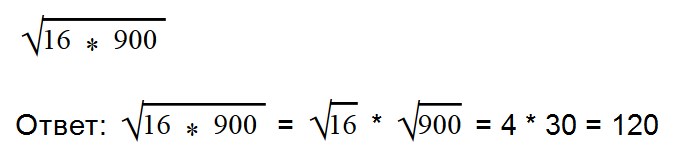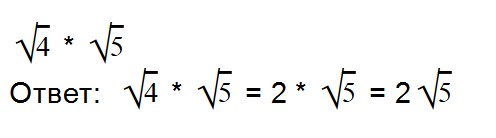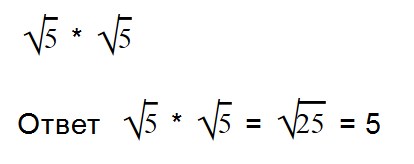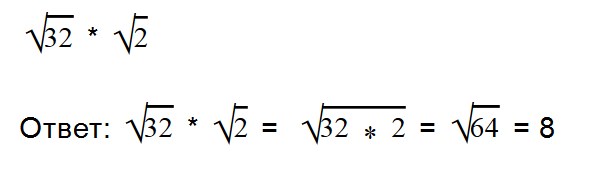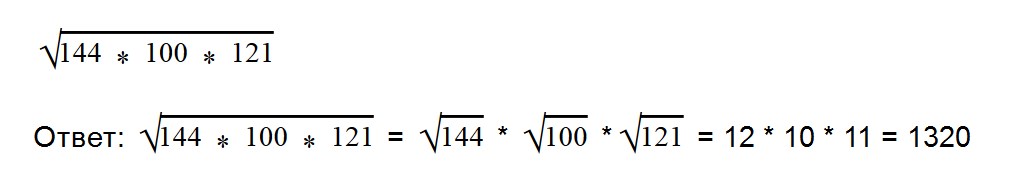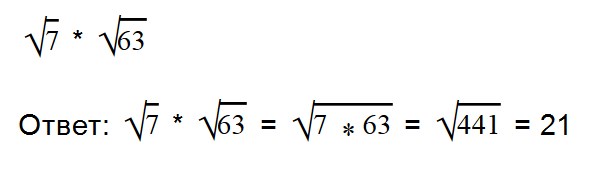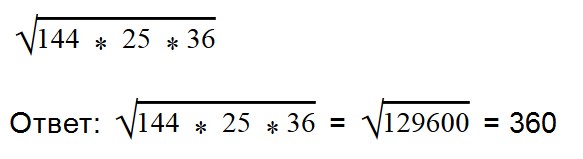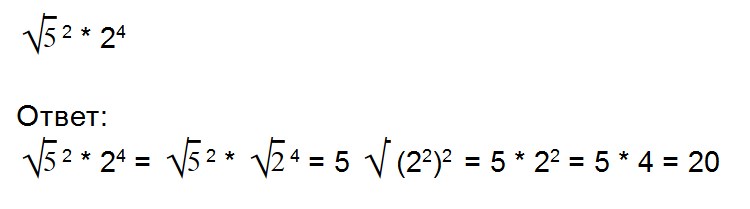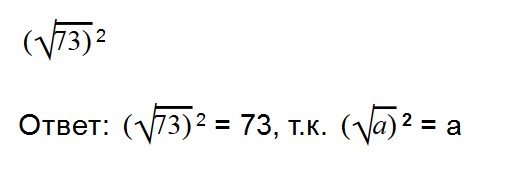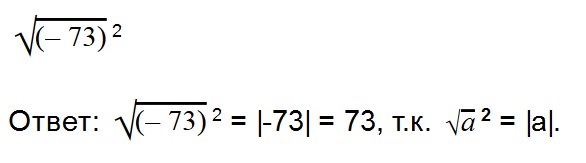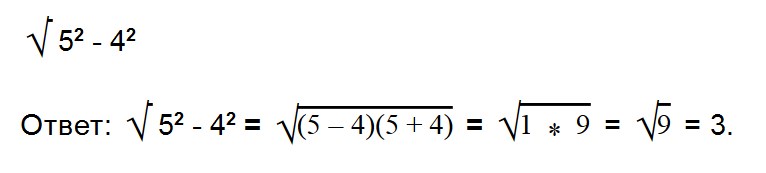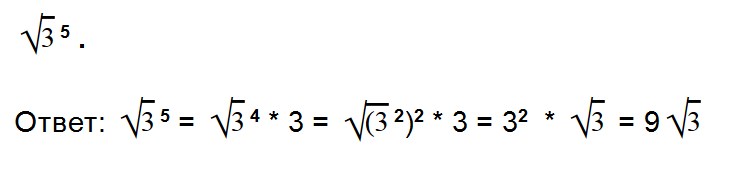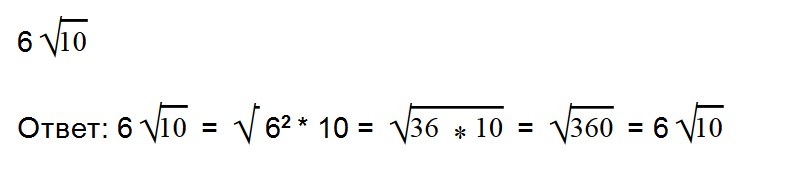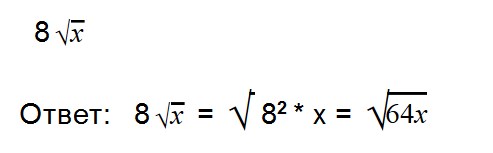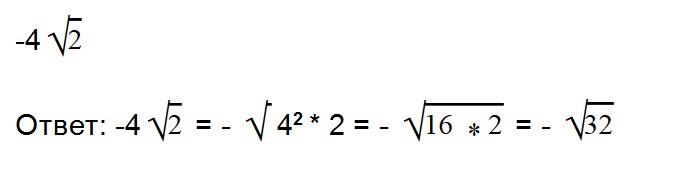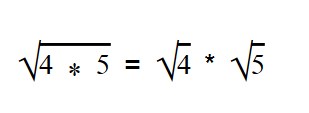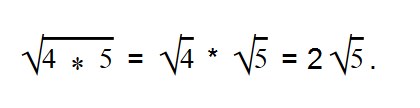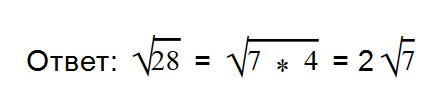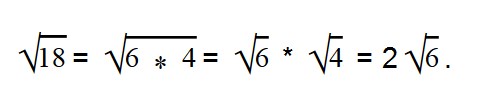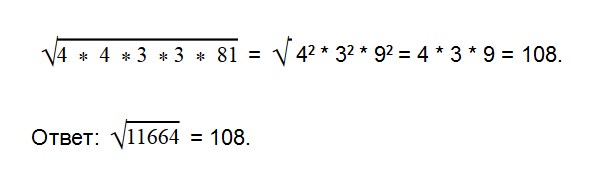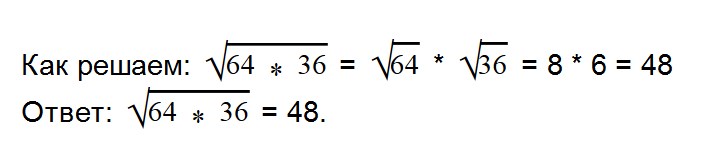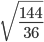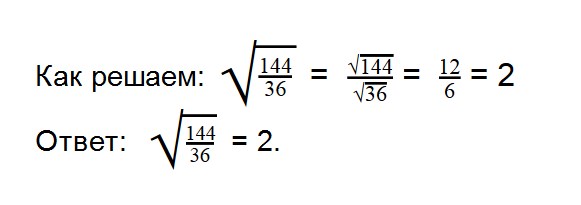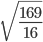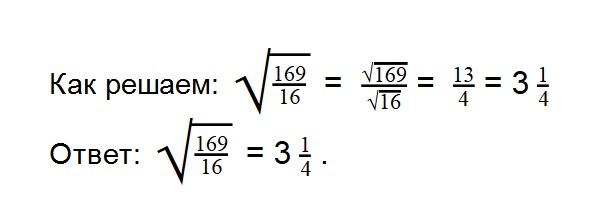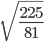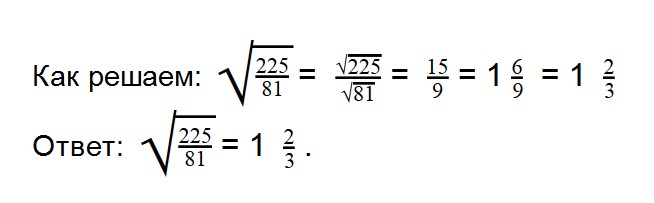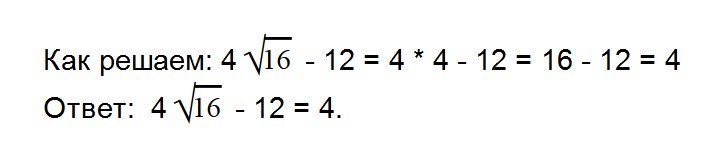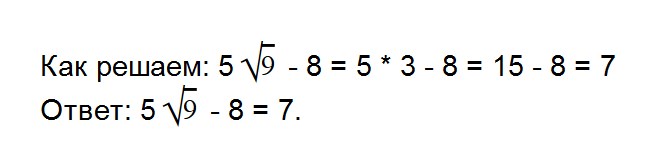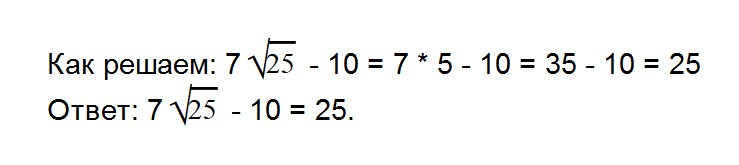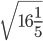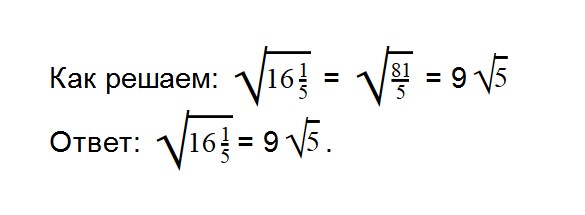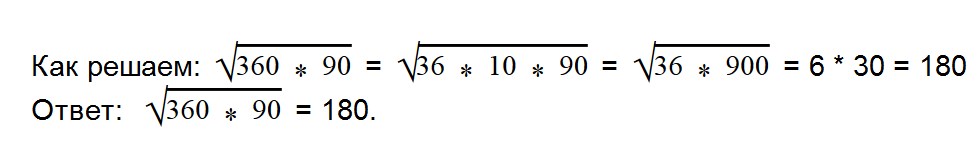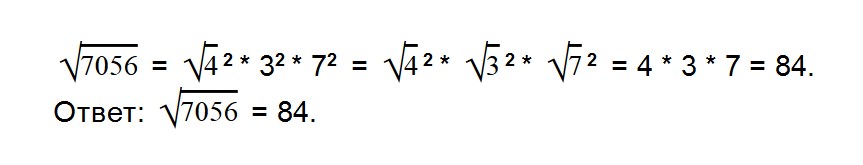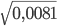| Вертикальная черта | |
|---|---|
| | |
| ◄ | x | y | z | ␡ | PAD | ► |
Вертика́льная черта́ — символ ASCII, имеющий код 0x7C (hex), 124 (dec). Этот символ пользователи UNIX называют «пайп», от англ. pipeline — конвейер. В первых, ещё советских, изданиях книг В. Э. Фигурнова название «pipe» было переведено как «символ трубопровода» [1] .
- Содержание
- Математика [ править | править код ]
- Форма Бэкуса — Наура [ править | править код ]
- Информатика [ править | править код ]
- Перенаправление ввода-вывода [ править | править код ]
- Языки программирования [ править | править код ]
- Псевдографика [ править | править код ]
- MediaWiki [ править | править код ]
- Электротехника [ править | править код ]
- Международный фонетический алфавит [ править | править код ]
- Разорванная вертикальная черта [ править | править код ]
- Здесь легко и интересно общаться. Присоединяйся!
- Что такое квадратный корень
- Что такое квадратный корень
- Разница между квадратным корнем и арифметическим квадратным уравнением
- Запись иррациональных чисел с помощью квадратного корня
- Извлечение корней
- Свойства арифметического квадратного корня
- Умножение арифметических корней
- Деление арифметических корней
- Возведение арифметических корней в степень
- Внесение множителя под знак корня
- Вынесение множителя из-под знака корня
- Сравнение квадратных корней
- Извлечение квадратного корня из большого числа
- Что значит вертикально и как выглядит вертикальная линия
- Таблица ASCII и вертикаль
- Применение в математике
- Полезное видео: вертикальная черта
- Применение в информатике
- Просто о сложном
Видео:Математический анализ, 15 урок, АссимптотыСкачать

Содержание
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Математика [ править | править код ]
Вертикальная черта используется в математике:
- A | B
: операция штриха Шеффера.
- | x |
: значение, находящееся между двумя вертикальными чертами, является модулем числа, или абсолютным значением.
- a | b
: число a
является делителем числа b
(часто произносится как « a
делит b
»).
- A = ( B | d ∣ ) )>
: матрица A
составлена путём приписывания столбца d
к матрице B
справа.
- P ( B | A )
: вероятностьсобытия B
при условии, что событие A
произошло (говорят «вероятность события B после A»).
- | a 11 ⋯ a 1 n ⋮ ⋱ ⋮ a n 1 ⋯ a n n | a_ &cdots &a_ vdots &ddots &vdots a_ &cdots &a_ end >>
— определитель матрицы.
Также используется двойная вертикальная черта:
- m ∥ n
: прямые или плоскости m
и n
параллельны.
- | | x | | L >
: норма элемента x
в метрике пространства L
.
Форма Бэкуса — Наура [ править | править код ]
Имеет смысл разделителя ИЛИ (разделяет 2 возможности):
Аналогичный смысл имеет в регулярных выражениях.
Видео:Математика без Ху!ни. Нахождение асимптот, построение графика функции.Скачать

Информатика [ править | править код ]
Перенаправление ввода-вывода [ править | править код ]
Используется в DOS и UNIX-системах для перенаправления стандартного потока вывода (stdout) одной программы в стандартный поток ввода (stdin) другой (конвейер). Например,
выведет список фруктов из файла fruits.txt, не имеющих ‘bad’ в качестве первых трёх символов, отсортированный по алфавиту. Такой способ передачи информации направляет потоки данных, подобно трубопроводу, поэтому его и назвали «pipeline» или просто «pipe» — труба. Соответственно знак вертикальной черты пользователи UNIX тоже называют «pipe».
Языки программирования [ править | править код ]
В C-подобных языках символ «|» служит для операции побитового «или» (дизъюнкция), а два таких символа, написанных слитно («||»), используются в операции логического «или».
Кроме того, в языках с «нестрогим» синтаксисом — shell-сценариях UNIX, в языке Perl — логический оператор «||» (ИЛИ) может использоваться для выполнения условного перехода, когда операция слева возвращает ложное значение. Таким образом может быть построена цепочка команд «сделай одно или сделай другое или сделай третье».
В приведённом примере в случае невозможности удаления одного и более файлов выводится сообщение.
Псевдографика [ править | править код ]
Наравне с символом «!» используется для рисования таблиц:
MediaWiki [ править | править код ]
В MediaWiki символ используется в разметке таблиц, а также в качестве разделителя параметров шаблонов.
Видео:Асимптоты функции. 10 класс.Скачать

Электротехника [ править | править код ]
В электротехнике запись R 1 | | R 2 ||R_ > 
Видео:Составляем уравнение прямой по точкамСкачать

Международный фонетический алфавит [ править | править код ]
В МФА символом вертикальной черты обозначают зубной щёлкающий согласный (двойной чертой — боковой щёлкающий согласный). Кроме того, вертикальные черты могут отделять просодические единицы друг от друга.
Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Разорванная вертикальная черта [ править | править код ]
На клавиатурах на клавише, предназначенной для ввода «|», традиционно рисуют разорванную вертикальную черту «¦». В настоящее время это отдельный символ « broken bar » с кодом U+00A6 (в HTML его можно обозначить как ¦ ).
В линейном формате редактора формул Microsoft Word (версии 2007 и более поздние) знак разорванной вертикальной черты применяется для создания дроби, но без черты [2] . Например, x¦y преобразуется в x y 
Здесь легко и интересно общаться. Присоединяйся!
вертикальные черточки означают МОДУЛЬ ЧИСЛА. или еще это называют абсолютной величиной.
наверное ты знакома с числовой прямой. во всяком случае. пользоваться шкалой линейки умеешь.
представь. чтоты играешь в игру. где на контрольных пунктах получаешь задания и вот такой пункт около двери твоего дома. вдоль которого идет тротуар а по дороге несутся машины.
задание гласит: сделай 8 шагов. у тебя 2 возможности – пойти вправо или влево. точка. от которой начинается отсчет 0. от нуля вправо – условились обозначать положительным направлением. влево – отрицательным. оно не плохое. оно в противоположную положительному.. .
в какую бы сторону ты ни пошла по заданию. ты сделаешь 8 шагов. вот смысл скобок.
самое простое объяснение-Модуль это расстояние. а от чего ( от 0) и до чего – смотри выше. надеюсь. понятно получилось.
эти так называемые палочки называются модуль
| Состояние | отпатрулирована |
В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeX, объяснения и примеры использования. Список и смысл обозначений соответствует международным стандартам ISO 31-11 и ISO 80000-2.
Кроме указанных символов, иногда используются их зеркальные отражения, например, A ⊂ B 
Знаки операций, или математические символы — знаки, которые символизируют определённые математические действия со своими аргументами.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Что такое квадратный корень
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Что такое квадратный корень
Определение арифметического квадратного корня ясности не добавляет, но заучить его стоит:
Арифметическим квадратным корнем из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен a.
Определение квадратного корня также можно представить в виде формул:
√a = x
x 2 = a
x ≥ 0
a ≥ 0
Из определения следует, что a не может быть отрицательным числом. То есть то, что стоит под корнем — обязательно положительное число.
Чтобы разобраться, почему именно так и никак иначе, давайте рассмотрим пример.
Попробуем найти корень из √-16
Здесь логично предположить, что 4, но давайте проверим: 4*4 = 16 — не сходится.
Если — 4, то -4 * -4 = 16, (минус на минус всегда дает плюс).
Получается, что ни одно число не может дать отрицательный результат при возведении его в квадрат.
Числа, стоящие под знаком корня, должны быть положительными.
Исходя из определения, значение корня также не должно быть отрицательным.
Здесь могут возникнуть резонные вопросы, почему, например, в примере x 2 = 16, x = 4 и x = -4.
Видео:Вертикальные углы. 7 класс.Скачать

Разница между квадратным корнем и арифметическим квадратным уравнением
Прежде всего, чтобы разграничить эти два понятия, запомните:
- x 2 = 16 не равно x = √16.
Это два нетождественных друг другу выражения.
- x 2 = 16 — это квадратное уравнение.
- x = √ 16 — арифметический квадратный корень.
Из выражения x 2 = 16 следует, что:
- |x| = √16, это значит, что x = ±√16 = ±4, x1 = 4, x2 = -4.
Если две вертикальные палочки возле x вводят вас в замешательство, почитайте нашу статью о модуле числа.
В то же самое время, из выражения x = √16 следует, что x = 4.
Если ситуация все еще кажется запутанной и нелогичной, просто запомните, что отрицательное число может быть решением только в квадратном уравнении. Если в решении «минус» — есть два варианта:
- Пример решен неверно
- Это квадратное уравнение.
Если вы извлекаете квадратный корень из числа, то можете быть уверены, вас ждет «положительный» результат.
Давайте рассмотрим пример, чтобы окончательно выяснить разницу между квадратным корнем и квадратным уравнением.
Даны два выражения:
Первое выражение — квадратное уравнение.
Второе выражение — арифметический квадратный корень.
Мы видим, что результатом решения первого выражения стали два числа — отрицательное и положительное. А во втором случае — только положительное.
Видео:Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Запись иррациональных чисел с помощью квадратного корня
Иррациональное число — это число, которое нельзя представить в виде обыкновенной дроби.
Чаще всего, иррациональные числа можно встретить в виде корней, логарифмов, степеней и т.д.
Примеры иррациональных чисел:
Чтобы упростить запись иррациональных чисел, математики ввели понятие квадратного корня. Давайте разберем пару примеров, чтобы увидеть квадратный корень в деле.
Дано уравнение: x 2 = 2.
Сразу сталкиваемся с проблемой, поскольку очевидно, что ни одно целое число не подходит.
Переберем числа, чтобы удостовериться в этом:
1 * 1 = 1,
2 * 2 = 4,
3 * 3 = 9.
Отрицательные числа дают такой же результат. Значит результатом решения не могут быть целые числа.
Решение следующее:
Строим график функции y = x 2 .
Отмечаем решения на графике: -√2; √2.
Если попробовать извлечь квадратный корень из 2 с помощью калькулятора, то результат будет следующий: √2 = 1,414213… .
В таком виде ответ не записывают — нужно оставить квадратный корень.
x 2 = 2.
x = √2
x = -√2.
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Извлечение корней
Решать примеры с квадратными корнями намного легче, если запомнить как можно больше квадратов чисел. Для этого воспользуйтесь таблицей — сохраните ее себе и используйте для решения задачек.
Таблица квадратов
Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:
- 1. Извлеките квадратный корень: √289
Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.
Влево — 1, вверх — 7.
- 2. Извлеките квадратный корень: √3025
Ищем в таблице число 3025.
Влево — 5, вверх — 5.
- 3. Извлеките квадратный корень: √7396
Ищем в таблице число 7396.
Влево — 8, вверх — 6.
- 4. Извлеките корень: √9025
Ищем в таблице число 9025.
Влево — 9, вверх — 5.
- 5. Извлеките корень √1600
Ищем в таблице число 1600.
Влево — 4, вверх — 0.
Извлечением корня называется нахождение его значение.
Видео:Метод "палочек и кружочков" в комбинаторикеСкачать

Свойства арифметического квадратного корня
У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.
- Корень произведения равен произведению корней
- Извлечь корень из дроби — это извлечь корень из числителя и из знаменателя
- Чтобы возвести корень в степень, нужно возвести в степень значение под корнем
Давайте потренируемся и порешаем примеры на все три операции с корнями. Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.
Видео:7 класс, 11 урок, Смежные и вертикальные углыСкачать

Умножение арифметических корней
Для умножения арифметических корней используйте формулу:
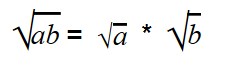 |
Примеры:
Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.
Если нет возможности извлечь корни из чисел, то поступаем так:
- Если множителей больше двух, то решается примерно точно так, как и с двумя множителями:
Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Деление арифметических корней
Для деления арифметических корней используйте формулу:
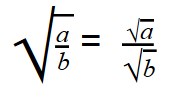 |
Примеры:
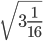
Ответ: смешанную дробь превращаем в неправильную (16 * 3) + 1 = 49
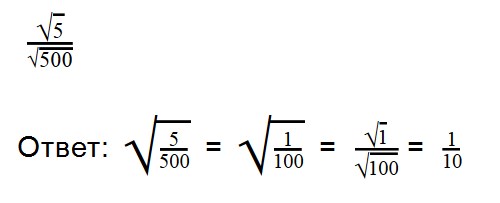
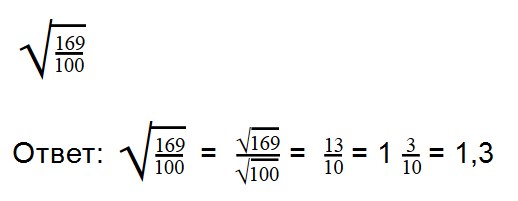
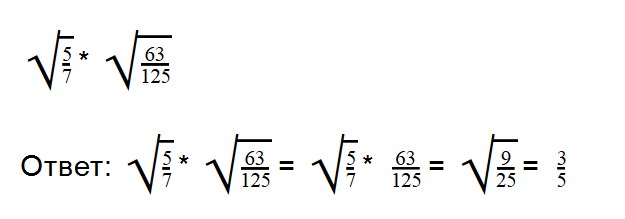
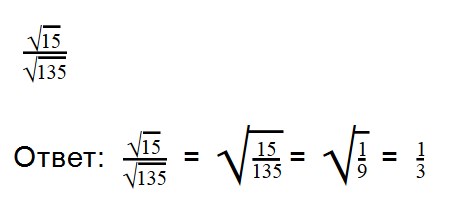
Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.
Видео:Алгебра 8 класс. Модуль числа с корнямиСкачать

Возведение арифметических корней в степень
Для возведения арифметического корня в степень используйте формулу:
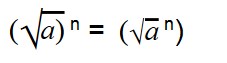 |
Примеры:
Эти две формулы нужно запомнить:
- (√a) 2 = a
- √a 2 = |a|
Повторите свойства степеней или запишитесь на курсы по математике, чтобы без труда решать такие примеры.
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Внесение множителя под знак корня
Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.
А теперь давайте разберемся, как вносить множитель под знак корня.
Дано выражение: 7√9
Число семь умножено на квадратный корень из числа девять.
Извлечем квадратный корень и умножим его на 7.
В данном выражение число 7 — множитель. Давайте внесем его под знак корня.
Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.
Вы помните, что (√a) 2 = a
Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.
7√9 = √7 2 * 9 = √49 * 9 = √49 * √9 = 7 * 3 = 21.
Формула внесения множителя под знак корня:
Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.
Видео:Перпендикулярные прямые. 6 класс.Скачать

Вынесение множителя из-под знака корня
С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.
Дано выражение в виде квадратного корня из произведения.
Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.
Извлекаем корень из всех имеющихся множителей.
В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:
Таким образом множитель выносится из-под знака корня.
Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.
Раскладываем подкоренное выражение на множители 28 = 7*4.
Извлекаем корень из 4. Множитель 7 оставляем под знаком корня.
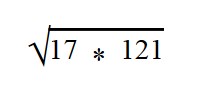
Ответ: по правилу извлечения квадратного корня из произведения,
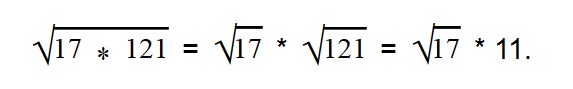
Так как вынесенный множитель должен стоять перед подкоренным знаком, то меняем их местами.
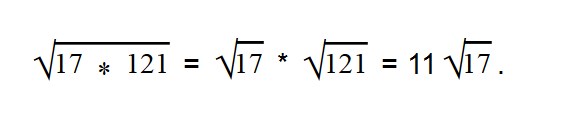
Ответ: Раскладываем выражение под корнем на множители 24 = 6 * 4.
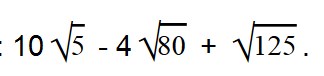
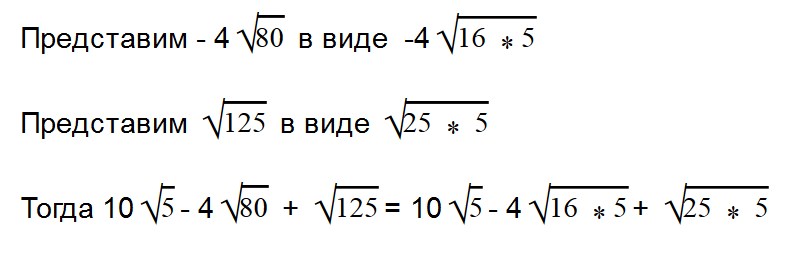
Вынесем в двух последних выражения множитель из-под знака корня.
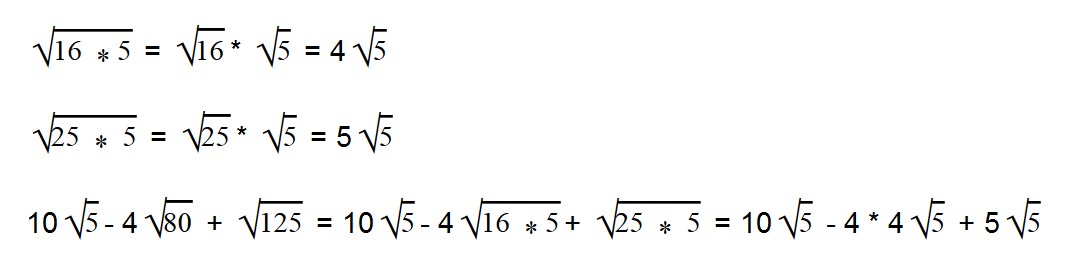
Умножаем (-4 * 4) = -16. Все остальное выражение записываем в неизменном виде.
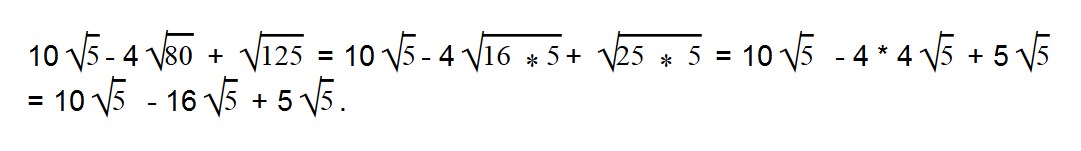
Мы видим, что во всем выражении есть один общий множитель — √5.
Выносим общий множитель за скобки:
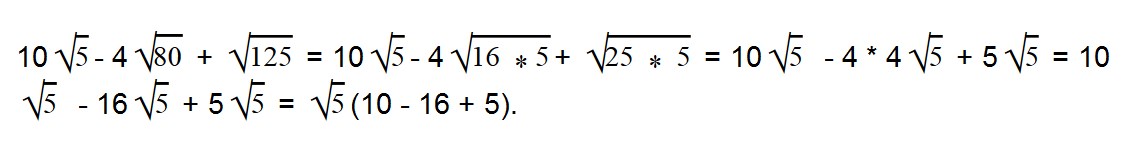
Далее вычисляем все, что в скобках:
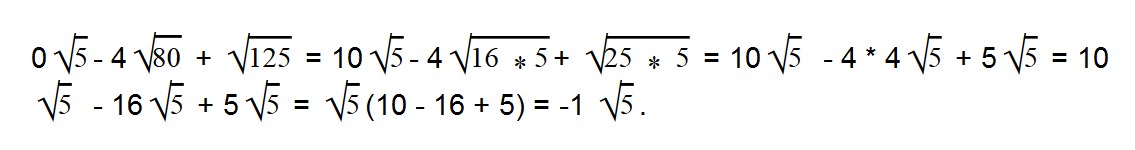
Видео:7 класс, 12 урок, Перпендикулярные прямыеСкачать

Сравнение квадратных корней
Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.
Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.
Если:
Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.
- Сравните два выражения: √50 и 9√5
Ответ: преобразовываем выражение 9√5.
9√5 = √81 * √5 = √81*5 = √405
Это значит, что 6√5 > √18.
Сравните два выражения: 7√12 и √20
Ответ: преобразовываем выражение 7√12.
7√12 = √49 * √12 = √49*12 = √588
Это значит, что 7√12 > √20.
Как видите, ничего сложного в сравнении арифметических квадратных корней нет.
Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.
Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.
Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.
Таких калькуляторов в интернете много, вот один из них.
Видео:Задачи: смежные и вертикальные углы. 4 задачи за 7 минут. Все о смежных и вертикальных углахСкачать

Извлечение квадратного корня из большого числа
Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.
Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.
Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:
- Определить «сотни», между которыми оно стоит.
- Определить «десятки», между которыми оно стоит.
- Определить последнюю цифру в этом числе.
Извлечь корень из большого числа можно разными способами — вот один из них.
Извлечем корень из √2116.
Наша задача в том, чтобы определить между какими десятками стоит число 2116.
Мы видим что, 2116 больше 1600, но меньше 2500.
Это значит, что число 2116 находится между 40 2 и 50 2 .
41, 42, 43, 44, 45, 46, 47, 48, 49.
Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.
Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.
Как пользоваться таблицей
4 2 = 16 ⇒ 6
5 2 = 25 ⇒ 5
6 2 = 36 ⇒ 6
7 2 = 49 ⇒ 9
8 2 = 64 ⇒ 4
9 2 = 81 ⇒ 1
Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.
Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.
Число 43, возведенное в квадрат, даст число, на конце которого — 9.
Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.
Таким образом, у нас остаются два варианта: 44 2 и 46 2 .
Далее вычисляем: 44 * 44 = 1936.
Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.
Еще пример. Извлечем корень из числа √11664
Разложим число 11664 на множители:
Запишем выражение в следующем виде:
Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.
Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.
- 1. Вычислите значение квадратного корня: √36
- 2. Вычислите значение квадратного корня: √64*36
- 3. Вычислите значение квадратного корня:
- 4. Вычислите значение квадратного корня:
- 5. Вычислите значение квадратного корня:
- 6. Вычислите значение выражения: 4√16 — 12
- 7. Вычислите значение выражения: 5√9 — 8
- 8. Вычислите значение выражения: 7√25 — 10
- 9. Вычислите значение квадратного корня:
- 10. Вычислите значение квадратного уравнения:
- 11. Вычислите значение квадратного уравнения:
- 12. Извлеките квадратный корень из числа √7056 удобным вам способом
Как решаем: - 13. Вычислите значение квадратного корня √0,81
Ответ: √0,81 = 0,9 - 14. Вычислите значение квадратного корня:
Как решаем:= 0,09
- 15. Вычислите значение выражения: 8√81 — 20
Как решаем: 8√81 — 20 = 8 * 9 — 20 = 72 — 20 = 52
Ответ: 8√81 — 20 = 52. - 16. Вычислите значение выражения: 13√100 — 15
Как решаем: 13√100 — 15 = 13 * 10 — 15 = 130 — 15 = 115
Ответ: 13√100 — 15 = 115. - 17. Вычислите значение выражения: √16 + 5√4
Как решаем: √16 + 5√4 = 4 + 5 * 4 = 4 + 20 = 24 Ответ: √16 + 5√4 = 24. - 18. Вычислите значение выражения: √36 + 2√9
Как решаем: √36 + 2√9 = 6 + 2 * 3 = 6 + 6 = 12
Ответ: √36 + 2√9 = 12. - 19. Вычислите значение выражения: 2√16 — 3√25
Как решаем: 2√16 — 3√25 = 2 * 4 — 3 * 5 = 8 — 15 = -7
Ответ: 2√16 — 3√25 = -7. - 20. Вычислите значение выражения: 3√81 — 5√9
Как решаем: 3√81 — 5√9 = 3*9 — 5 * 3 = 27 — 15 = 12
Ответ: 3√81 — 5√9 = 12. - 21. Вынесите множитель из-под знака корень: √60
Как решаем: √60 = √15 * √4 = 2√15
Ответ: √60 = 2√15. - 22. Вынесите множитель из-под знака корень: √160
Как решаем: √160 = √16 * √10 = 4√10
Ответ: √160 = 4√10. - 23. Внесите множитель под знак корня: 6√7
Как решаем: √6 2 * 7 = √36 * √7 = √252
Ответ: 6√7 = √252. - 24. Внесите множитель под знак корня: 8√2
Как решаем: 8√2 = √8 2 * 2 = √64 * √2 = √128 Ответ: 8√2 = √128. - 25. Внесите множитель под знак корня: 9√5
Как решаем: 9√5 = √9 2 * 5 = √81 * √5 = √405
Ответ: 9√5 = √405. - 26. Упростите выражение: (5 — √2) 2
Как решаем: (5 — √2) 2 = 5 2 — 2 * 5 * √2 + (√2) 2 = 25 — 10√2 + 2 = 27 — 10√2.
Ответ: (5 — √2) 2 = 27 — 10√2. - 27. Вычислите значение выражения: 3√49 — 3√25
Как решаем: 3√49 — 3√25 = 3 * 7 — 3 * 5 = 21 — 15 = 6
Ответ: 3√49 — 3√25 = 6. - 28. Вычислите значение квадратного корня: √484 * √576
Как решаем: √484 * √576 = 22 * 24 = 528
Ответ: √484 * √576 = 528. - 29. Вычислите значение квадратного корня: √625 * √81
Как решаем: √625 * √81 = 25 * 9 = 225
Ответ: √625 * √81 = 225. - 30. Найдите значение выражения: 3√100 — √144
Как решаем: 3100 — 144 = 3 * 10 — 12 = 18
Ответ: 3√100 — √144 = 18.
- 0 0 0 0 0 0
Вебинар : Гаджеты: как вернуть ребёнка в реальность среда, 23 февраля в 19:00 МСК
Видео:Смежные и вертикальные углы. Практическая часть - решение задачи. 7 класс.Скачать

Что значит вертикально и как выглядит вертикальная линия
Казалось бы, что каждому человеку должно быть известно, что обозначают такие термины как «вертикально», «горизонтально». Однако даже взрослые люди зачастую путаются это вверх или нет. В данной статье мы попробуем разобраться, какое положение считается вертикальным, как и где принято использовать это обозначение. Более того, мы поговорим и о том, какое значение отводится обычной вертикальной черте в некоторых школьных науках.
Таблица ASCII и вертикаль
Сперва поговорим о том, что же должен представлять человек, когда слышит определение «вертикальная черта». В первую очередь, это обозначение используется именно в ASCII. Вам ничего не говорит данная аббревиатура? И это вполне нормально, поскольку данная шифровка будет знакома исключительно людям, работа которых связана с кодированным текстом.
Это интересно! Считаем правильно: как находить процент от суммы и числа
Для простых обывателей поясним, что ASCII представляет собой достаточно большую таблицу. В ней собраны различные коды. Каждый из этих кодов соответствует печатным и непечатным символам, которые широко используются.

Обратите внимание! Речь идет именно о числовых кодах. Впервые эта таблица была разработана специалистами из Соединенных Штатов Америки в 60-х годах. Практически сразу после разработки она была стандартизирована и после этого начала активно использоваться.
В таблице можно найти и такой символ, как вертикальная линия. Ее код – 0x7C (hex), 124 (dec).
Примечательно, что пользователи операционной системы под названием UNIX, предпочитают именовать данный символ не иначе как «пайп». С английского языка слово «pipeline» можно перевести как конвейер. Но в Советском Союзе понять и принять данную терминологию не смогли. Книги В. Э. Фигурнова, первые издания которых являются советскими, пестрели необычным сравнением вертикальной линии с трубопроводом. Именно поэтому ее и начали именовать как символ трубопровода, заменив тем самым ходовое наименование «pipe».
Это интересно! Как найти и чему будет равна длина окружности
Применение в математике
Наверняка, каждый школьник, который не прогуливал уроки и добросовестно выполнял домашние задания, известно, как выглядит вертикаль. Ведь в математике обозначение используется довольно часто. Причем вариантов применения имеется немало.
Рассмотрим более подробно каждый из них и тем самым немного вспомним школьную программу.
- |x| знакомое многим обозначение. Значение, которое находится между двумя вертикальными чертами, это абсолютное значение. Тоже никогда не слышали? Тогда напомним о другом термине, которым принято обозначать абсолютное значение. И это – модуль. Следовательно, линия, идущая вниз, обозначает именно модуль.
- m || n – разделение двумя вертикальными чертами принято считать обозначением параллели. Иными словами, данные прямые (плоскости) всегда будут параллельными, если их разделяет подобный символ.
- a|b – в такой формуле вертикальная линия представляет собой разделитель. То есть число a делит число b.
- p(b|a) – более сложная формула. Разделение в виде вертикальной черты говорит о том, что некое событие b возможно только при условии, что произойдет событие a.
Вышеперечисленные формулы и обозначения не являются единственными. В математике достаточно много и других примеров использования вертикальной черты. Стоит упомянуть и о том, что она часто используется в другой науке, которую тоже преподают в школе.
Полезное видео: вертикальная черта
Применение в информатике
Специалисты, которые работают с такими системами как DOS и UNIX, знают, что такое вертикальная линия, поскольку часто с ней работают. Подобное объясняется тем, что именно это обозначение используется для Stdout. А что же представляет собой Stdout? Все просто – это процесс, который обозначает перенаправление стандартного потока вывода определенной программы в другой конвейер.
Чтобы было более понятно, рассмотрим такую сложную формулу: cat fruits.txt | grev –v ^bad | sort. Но сразу отметим, что она сложная только на первый взгляд. В действительности программист задал простой алгоритм. С его помощью можно вывести на экран список фруктов, который содержится в файле под названием fruits.txt.
Это интересно! Изучаем символы: как обозначается в математике площадь
Но при этом можно будет увидеть только те фрукты, в названии которых в первых 3-х символах нет «bad». Более того, выведенный список будет сразу отсортирован по алфавиту. Все просто, не так ли? Но какая же формула натолкнула программистов на мысль сравнить вертикаль с трубопроводом?
Та, что приведена выше. На примере этой формулы можно понять, почему же российским программистам пришло в голову сравнить данный символ с трубопроводом. Описанный метод передачи информации направляет поток данных по тому же принципу работы, что и обычный трубопровод. Именно поэтому программисты из Советского Союза посчитали, что термин «pipe», пришедший с Запада, можно заменить на другой «трубопровод». Ведь по вертикали это значит и вниз, и вниз.

Просто о сложном
Практически у каждого человека, который прочитал вышеизложенный текст, гарантированно возникла мысль, что разобраться в том,какая линия вертикальна, сложно. Но в действительности это не так. Итак, сейчас попробуем простым и понятным языком объяснить, что же представляет собой вертикаль.
Это интересно! Урок геометрии: как найти по формуле периметр треугольника
Вертикаль – это направление, которое перпендикулярно горизонтальной плоскости. А теперь вспомним, что такое горизонтальная плоскость. Представьте себе горизонт. Представили? Вот вам и горизонтальная плоскость. Следовательно, плоскость, которая будет располагаться по отношению к горизонту перпендикулярно, должна считаться вертикальной чертой. То есть вертикально, как уже было написано, это вверх и вниз одновременно.