| Коэффициенты многочлена разделенные пробелами |
| Заданный многочлен имеет вид | ||||
| Нижняя граница действительных корней многочлена | ||||
| Верхняя граница действительных корней многочлена | ||||
Рассмотрим еще одну задачу связаннуюс полиномами. Когда мы пытаемся решить такое уравнение численно, то нам необходимо знать, в каких пределах могут находится действительные корни этого полинома. Эти знания позволят нам быстрее обеспечить сходимость при компьютерных вычислениях. Это позволит при прорисовке полинома в виде графика, выбрать такой масштаб, что бы мы увидели все пересечения функции с осью абсцисс. Итак, как же формулы мы будем использовать для решения задачи? Если нам известен полином вида То разделив его на a0 мы получаем Правило утверждает, что если среди коэффицентов есть отрицательные числа и -первое из них, и также есть отрицательный коэффицент A который является самым большим (в абсолютном значении), то действительные корни этого полинома не превышают число Нижнюю границу можно определить по аналогичной формуле, вычислив значения функции коэффицентов при -x Давайте рассмотрим пример Разделим на 3 , что бы первый член полинома был равен единице. Первый отрицательный коэффициент который мы встречаем это он стоит на второй позиции ( ) Значение А=9, так как 9 явлется максимальном в абсолютном выражении числом из всех отрицательных коэффициентов полинома. Таким образом верхняя граница действительных корней Теперь определяем нижнюю границу Разделим полином на -3, что бы первый член полинома был равен единице. Первый отрицательный коэффициент который мы встречаем это он стоит на первой позиции ( ) Таким образом нижняя граница действительных корней Следовательно, все действительные корни заданного многочлена находятся в пределах Бот позволяет выполнять эти вычисления автоматически и при заданных действительных коэффициентах давать правильные результаты. Единственное замечание, не стоит вводить в качестве коэффициентов комплексные числа. Результат будет непредсказуем. Содержание
Видео:Найти корень уравнения на заданном интервале (MathCad)Скачать  3.1. Отделение корней нелинейного уравненияОтделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a, b], которому он принадлежит. На первом этапе определяется число корней, их тип. Определяется интервал, в котором находятся эти корни, или определяются приближенные значения корней. В инженерных расчетах, как правило, необходимо определять только вещественные корни. Задача отделения вещественных корней решается Аналитическими и Графическими методами. Аналитические методы основаны на функциональном анализе. Для алгебраического многочлена n-ой степени (полинома) с действительными коэффициентами вида Pn(x) = an x n + an-1xn-1 +. +a1x+ a0 = 0, (an >0) (3.2) Верхняя граница положительных действительных корней
Где: k ³ 1 – номер первого из отрицательных коэффициентов полинома; B – максимальный по модулю отрицательный коэффициент. Нижнюю границу положительных действительных корней Если для этого уравнения по формуле Лагранжа верхняя граница равна R1, то
Тогда все положительные корни многочлена лежат в интервале
Интервал отрицательных действительных корней многочлена определяется с использованием следующих вспомогательных функций.
Рассмотрим пример отделения корней с использованием этого аналитического метода. Методом Лагранжа определим границы положительных и отрицательных корней многочлена. 3×8 – 5×7 – 6×3 – x – 9 = 0 K = 1 B = |– 9| an = 3
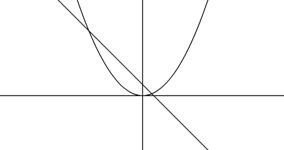
k = 8 B = 3 an = 9 Отсюда границы положительных корней 0,5 ≤ x+ ≤ 4
K = 1 B = 6 an = 9
Следовательно, границы отрицательных корней –2 ≤ x– ≤ –0,6 Формула Лагранжа позволяет оценить интервал, в котором находятся все действительные корни, положительные или отрицательные. Поэтому, для определения расположения каждого корня необходимо проводить дополнительные исследования. Для трансцендентных уравнений не существует общего метода оценки интервала, в котором находятся корни. Для этих уравнений оцениваются значения функции в особых точках: разрыва, экстремума, перегиба и других. На практике получил большее распространение Графический метод приближённой оценки вещественных корней. Для этих целей строится график функции по вычисленным её значениям. Графически корни можно отделить 2-мя способами: 1. Построить график функции y = f(x) и определить координаты пересечений с осью абсцисс− это приближенные значения корней уравнения.На графике 3 корня. Рис. 3.1 Отделение корней на графике f(x). 2. Преобразовать f(x)=0 к виду j(x) = y(x), где j(x) и y(x) – элементарные функции, и определить абсциссу пересечений графиков этих функций. На графике 2 корня. Рис. 3.2 Отделение корней по графикам функций j(x) и y(x). Графический метод решения нелинейных уравнений широко применяется в технических расчётах, где не требуется высокая точность. Для отделения вещественных корней можно использовать ЭВМ. Алгоритм отделения корней основан на факте Изменения знака функции в окрестности корня. Действительно, если корень вещественный, то график функции пересекает ось абсцисс, а знак функции изменяется на противоположный. Рассмотрим Схему алгоритма отделения корней нелинейного уравнения на заданном отрезке в области определения функции. Алгоритм позволяет определить приближённые значения всех действительных корней на отрезке [a, b]. Введя незначительные изменения в алгоритм, его можно использовать для определения приближённого значения максимального или минимального корня. Приращение неизвестного Δx не следует выбирать слишком большим, чтобы не «проскочить» два корня. Недостаток метода – использование большого количества машинного времени. Видео:Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать  Реферат: Отделение корней. Графический и аналитический методы отделения корней
3. Аналитический метод (табличный или шаговый).Для отделения корней полезно помнить следующие известные теоремы: 1) если непрерывная функция f(x) принимает значения разных знаков на концах отрезка [a,b], т.е. f(a)f(b) 0, значит корня на отрезке [0;0.5] нет. f(0.5)f(1) 0, значит корня на отрезке [0.5;0.75] нет. 🔍 ВидеоАлгоритмы. Нахождение корней уравнений методом деления отрезка пополам.Скачать  Отбор корней по окружностиСкачать  Три способа отбора корней в задании 13 ЕГЭ профильСкачать  Тригонометрия 8. Отбор корнейСкачать  Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать  Курс по численным методам: Отделение действительных корней алгебраический уравнений | Занятие 1Скачать  МЕРЗЛЯК-7. ЛИНЕЙНЫЕ УРАВНЕНИЯ. ПАРАГРАФ-2Скачать  Как решают уравнения в России и СШАСкачать  Решение квадратных уравнений. Дискриминант. 8 класс.Скачать  Численное решение уравнений, урок 3/5. Метод хордСкачать  Формула корней квадратного уравнения. Алгебра, 8 классСкачать  5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать  Решить квадратное уравнение. MS Excel. Поиск решенияСкачать  ЕГЭ по математике. Профильный уровень. Задание 5. Найдите корень уравненияСкачать  [3] Параметры аналитика с нуля. Расположение корней. Решаем задачи по алгоритму.ЭкстраСкачать ![[3] Параметры аналитика с нуля. Расположение корней. Решаем задачи по алгоритму.Экстра](https://i.ytimg.com/vi/tJ2WXAHcF1g/0.jpg) |
 определяется по формуле Лагранжа (Маклорена):
определяется по формуле Лагранжа (Маклорена): , (3.3)
, (3.3) можно определить из вспомогательного уравнения
можно определить из вспомогательного уравнения (3.4)
(3.4) =
=  (3.5)
(3.5) .
. и
и  .
. ≤x–≤
≤x–≤ 

 .
. = 4
= 4 9×8 + x7 + 6×5 + 5x – 3 = 0
9×8 + x7 + 6×5 + 5x – 3 = 0
 3×8 + 5×7 + 6×3 + x – 9 = 0
3×8 + 5×7 + 6×3 + x – 9 = 0
 9×8 – x7 – 6×5 – 5x – 3 = 0
9×8 – x7 – 6×5 – 5x – 3 = 0


 Министерство образования и науки РФ
Министерство образования и науки РФ


 при
при  что уже свидетельствует о наличии хотя бы одного корня.
что уже свидетельствует о наличии хотя бы одного корня.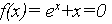 видим, что
видим, что 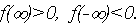 Обнаружив, что
Обнаружив, что 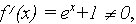 устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).
устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).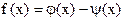 и строить графики функций
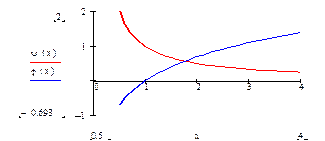
и строить графики функций 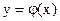 и
и 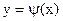 . Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох.
. Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох.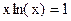 .
.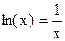 , т.е.
, т.е. 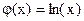 и
и 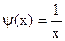 .
.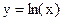 и
и 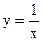 .
.