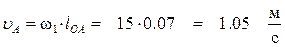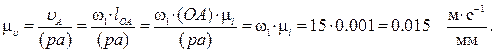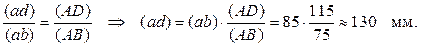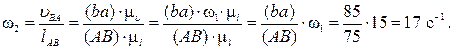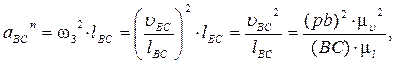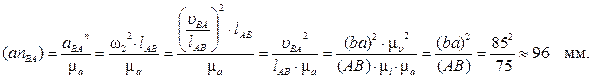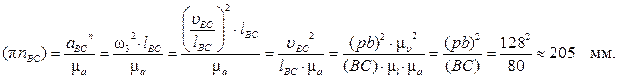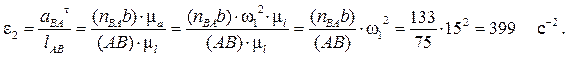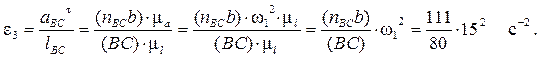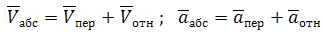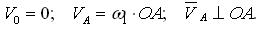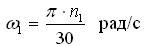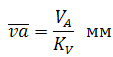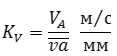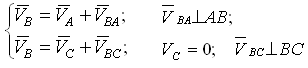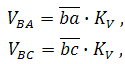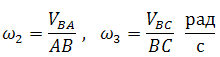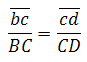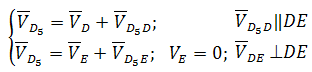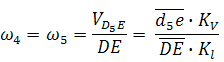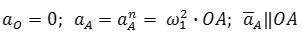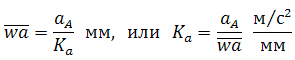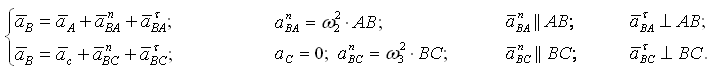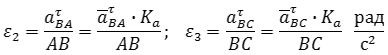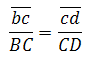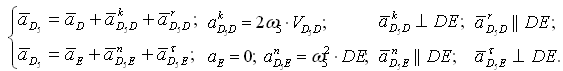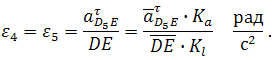Тема: Построение планов скоростей и ускорений механизма, образованного группой Ассура 2–го класса 1–го вида.
Построение плана скоростей
Планы скоростей и ускорений механизма строятся после решения задачи о его положении, причём построение планов проводится для отдельных групп Ассура, которые образовали механизм. Вначале строится план скоростей (ускорений) группы, которая присоединена элементами своих внешних кинематических пар к ведущему звену и стойке, затем строятся планы скоростей (ускорений) второй и т.д. групп, взятых в той же последовательности, в какой они присоединяются при образовании механизма.
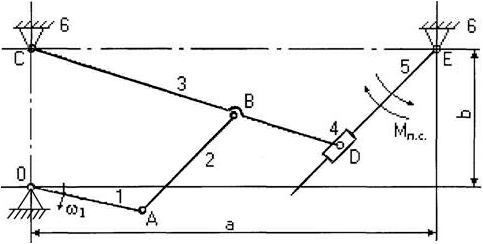
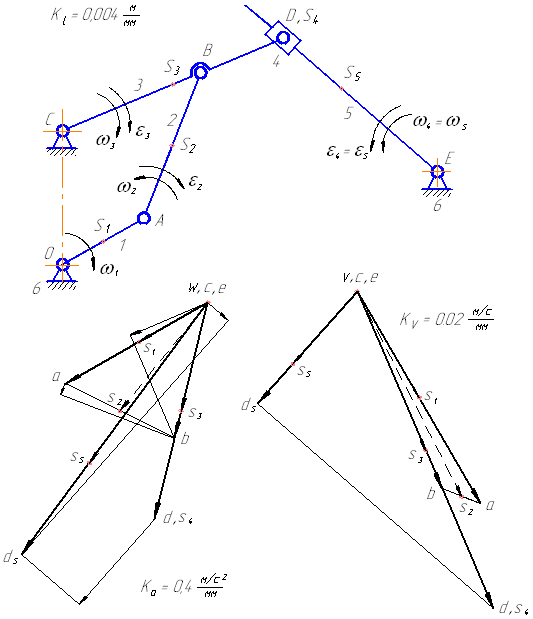
Рассмотрим двухкривошипный шарнирный четырёхзвенник. Данные: lOA = 0.07 м, lOC = 0.04 м, lBC = 0.08 м, lAB = 0.075 м, lBD = 0.04, j1 = 30°, угловая скорость кривошипа OA постоянна и равна w1 = 15 c – 1 (рис. 1).
План положения механизма
Сначала строим план заданного положения механизма. Масштаб длин принимаем равным ml = 0.001 м /мм. Вычисляем длины отрезков, изображающие на чертеже звенья.
Для каждого положения механизма определяются скорости точек графическим методом. Вначале определяем скорость точки A, принадлежащей ведущему звену, которое вращается равномерно с постоянной угловой скоростью w1. Скорость этой точки по модулю равна
и направлена перпендикулярно оси звена OA в сторону вращения. Отложим от произвольной точки p, называемой полюсом плана скоростей, отрезок (pa). Длину отрезка (pa) выбираем равной (OA). (pa) = (OA) = 70 мм. Вычисляем масштабный коэффициент скоростей:
Строим план скоростей для группы звеньев 2 и 3. Оба звена совершают плоскопараллельное движение. Из теоретической механики известно, что скорость любой точки B плоской фигуры геометрически складывается из скорости какой-нибудь точки A, принятой за полюс, и скорости, которую точка B получает при вращении фигуры вокруг этого полюса.В этой группе звеньев все пары вращательные. Определяем скорость точки B по следующим двум векторным уравнениям:
где 

Построение плана скоростей ведём в такой последовательности. Строим решение первого векторного уравнения, указанного выше: из точки a проводим направление скорости изображающий 
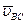
Определяем скорость точки B: uB = (pb)×mu = 128×0.015 = 1.92 м/c.
Определяем скорость точки D: uD = (pd)×mu = 169×0.015 » 2.54 м/c.
Определяем угловую скорость звена AB:
План скоростей механизма
 |
Направление угловой скорости w2 звена AB может быть определено следующим образом. Мысленно прикладывая вектор 
Определяем угловую скорость звена BC:
Направление угловой скорости w3 звена BC определяется таким же образом, как и w2. Мысленно прикладывая вектор 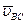
Построение плана ускорений
Ускорения точек находятся методом плана ускорений. Вначале определяем скорость точки A, принадлежащей ведущему звену, которое вращается равномерно с постоянной угловой скоростью w1. Полное ускорение точки A определяется по формуле 
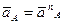
где 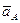

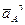
и направленное параллельно линии OA от точки A к точке O (к центру кривизны траектории);

и направленное параллельно линии AB от точки B к точке A ( 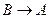

(e2 — угловое ускорение звена AB, пока нам неизвестное) и направленное перпендикулярно линии AB;
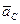
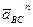
и направленное параллельно линии BC от точки B к точке C ( 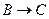
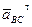
(e3 — угловое ускорение звена BC, пока нам неизвестное) и направленное перпендикулярно линии BC.
Построение плана ускорений ведём в следующей последовательности. Строим решение первого векторного уравнения, указанного выше, для чего от полюса плана p откладываем отрезок (pa), изображающий ускорение 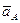
От точки a откладываем отрезок (anBA), изображающий ускорение 
Через точку nBA проводим направление ускорения 
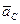
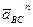
Через точку nBC проводим направление ускорения 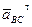

Соединив точку d с полюсом плана p, получаем отрезок (pd), изображающий абсолютное ускорение точки D.
Величины абсолютных ускорений точек B и D определяются так:
По правилу подобия найдём ускорения центров масс подвижных звеньев. Точки S1, S2 и S3 находятся на серединах соответствующих звеньев. На плане ускорений это будут векторы: (ps1), (ps2) и (ps3). Определяем абсолютные величины ускорений этих центров масс:
Величина углового ускорения звена AB равна:
Направление углового ускорения e2 звена 2 (звена AB) может быть определено следующим образом. Перенося мысленно вектор 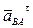
Величина углового ускорения звена BC равна:
Направление углового ускорения e3 звена 3 (звена BC) может быть определено таким же образом, как и e2. Перенося мысленно вектор 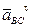
- iSopromat.ru
- Начальный механизм
- Сложение скоростей и ускорений — справочник студента
- Начальный механизм
- Кинематический расчет механизма
- Построение траектории движения точки
- Построение плана скоростей для заданного положения механизма
- Кинематика — Физика — Теория, тесты, формулы и задачи — Обучение Физике, Онлайн подготовка к ЦТ и ЕГЭ
- Основные теоретические сведения
- Система СИ
- Путь и перемещение
- Средняя скорость
- Равноускоренное прямолинейное движение
- Свободное падение по вертикали
- Горизонтальный бросок
- Бросок под углом к горизонту (с земли на землю)
- Сложение скоростей
- Равномерное движение по окружности
- Сложное движение точки. Теорема Кориолиса
- Сложное (составное) движение точки
- Относительная скорость и ускорение
- Переносная скорость и ускорение
- Абсолютная скорость и ускорение
- Теорема о сложении скоростей
- Доказательство
- Теорема Кориолиса о сложении ускорений
- Доказательство
- Закон сложения скоростей
- Преобразование координат и времени
- Закон сложения ускорений для поступательного движения
- Теорема Кориолиса
- 🎬 Видео
Видео:ЛЕКЦИЯ #5. ТММ. ПЛАН СКОРОСТЕЙ.Скачать

iSopromat.ru
Рассмотрим порядок построения планов скоростей и ускорений точек звеньев на примере кинематического исследования плоского рычажного механизма (рисунок 1).
Планом скоростей (ускорений) механизма называют чертеж, на котором скорости (ускорения) различных точек изображены в виде векторов, показывающих направления и величины (в масштабе) этих скоростей (ускорений) в данный момент времени.
Абсолютное движение любой точки звена может быть составлено из переносного и относительного. За переносное принимается известное движение какой-либо точки. Относительное – движение данной точки относительно той, движение которой принято за переносное:
На плане абсолютные скорости (ускорения) изображаются векторами, выходящими из полюса плана.
На конце вектора абсолютной скорости (ускорения) ставится строчная (маленькая) буква, соответствующая той точке механизма, скорость (ускорение) которой данный вектор изображает. Отрезок, соединяющий концы векторов абсолютных скоростей, представляет собой вектор относительной скорости соответствующих точек.
Рисунок 1 – Кинематическая схема плоского рычажного механизма
Рассмотрим построение планов для механизма, представленного на рисунке 1. Вначале рассматривается начальный механизм, а далее решение ведется по группам Ассура в порядке их присоединения.
По вычисленному значению VA выбираем масштаб плана скоростей KV и из произвольного полюса откладываем отрезок va изображающий эту скорость:
Можно также назначать отрезок va а масштаб KV вычислять:
Истинные значения (в м/с) относительных скоростей VBA и VBC определяются после построения плана умножением соответствующих отрезков (в мм) на масштаб плана:
а зная их, можно определить и угловые скорости звеньев 2 и 3:
Скорость точки D на плане скоростей можно определить по подобию. (Если известны скорости двух точек одного и того же звена, то скорость любой третьей точки этого же звена можно определить, построив на плане скоростей фигуру, подобную фигуре, образованной этими же буквами на звене механизма). Точки С, В , D на звене 3 лежат на одной прямой. На плане строим отрезок сd, соблюдая условие подобия:
Группа Ассура второго класса 3-го вида (звенья 4,5) :
где D5 — точка, находящаяся на звене 5 под точкой D. После определения скорости движения точки D5 относительно точки E можно вычислить угловую скорость звеньев 4 и 5 ( ω4=ω5 , т. к. эти звенья соединяются поступательной парой):
Примечание: в данном случае размер DE является величиной переменной (т.е. в задании он отсутствует), поэтому в каждом положении механизма он определяется через отрезок на чертеже и масштаб длин.
План ускорений строится в таком же порядке.
Видео:Построение плана скоростей. ТММСкачать

Начальный механизм
Ускорение точки A состоит только из нормальной составляющей, т.к. задана постоянная угловая скорость первого звена ( ω1=соnst ):
По вычисленному значению ускорения точки A выбирается масштаб плана ускорений и определяется отрезок на плане, соответствующий этому ускорению (или вычисляется масштаб плана ускорений по выбранному отрезку, изображающему ускорение точки A):
Здесь точка w – полюс плана ускорений.
Группа Ассура (звенья 2,3) второго класса 1-го вида:
После построения определяются a τ BA и a τ BC , по которым можно вычислить угловые ускорения звеньев 2 и 3:
Ускорение точки D определяем по подобию так же, как определяли скорость этой точки:
Рисунок 5 – Планы скоростей и ускорений для заданного положения механизма
Группа Ассура (звенья 4,5) второго класса 3-го вида:
Для определения направления a k D5D надо вектор VD5D повернуть на 90° в направлении ω5 . Угловые ускорения:
При силовом расчете необходимо иметь ускорения центров масс ( asi ), которые на плане ускорений определяются методом подобия.
Планы скоростей и ускорений для первого положения заданного механизма приведены на рисунке 5.
Уравнение планов скоростей и ускорений для каждой группы Ассура приведены в таблице 1.
Таблица 1 – Кинематический анализ групп Ассура II класса методом планов
Видео:ЛЕКЦИЯ #9. ТММ. ПЛАН СКОРОСТЕЙ.Скачать

Сложение скоростей и ускорений — справочник студента
Планом скоростей (ускорений) механизма называют чертеж, на котором скорости (ускорения) различных точек изображены в виде векторов, показывающих направления и величины (в масштабе) этих скоростей (ускорений) в данный момент времени.
Абсолютное движение любой точки звена может быть составлено из переносного и относительного. За переносное принимается известное движение какой-либо точки. Относительное – движение данной точки относительно той, движение которой принято за переносное:
На плане абсолютные скорости (ускорения) изображаются векторами, выходящими из полюса плана.
На конце вектора абсолютной скорости (ускорения) ставится строчная (маленькая) буква, соответствующая той точке механизма, скорость (ускорение) которой данный вектор изображает. Отрезок, соединяющий концы векторов абсолютных скоростей, представляет собой вектор относительной скорости соответствующих точек.
Рисунок 1 – Кинематическая схема плоского рычажного механизма
Рассмотрим построение планов для механизма, представленного на рисунке 1. Вначале рассматривается начальный механизм, а далее решение ведется по группам Ассура в порядке их присоединения.
По вычисленному значению VA выбираем масштаб плана скоростей KV и из произвольного полюса откладываем отрезок va изображающий эту скорость:
Можно также назначать отрезок va а масштаб KV вычислять:
Группа Ассура второго класса 1-го вида (звенья 2, 3):
Истинные значения (в м/с) относительных скоростей VBA и VBC определяются после построения плана умножением соответствующих отрезков (в мм) на масштаб плана:
а зная их, можно определить и угловые скорости звеньев 2 и 3:
Скорость точки D на плане скоростей можно определить по подобию.
(Если известны скорости двух точек одного и того же звена, то скорость любой третьей точки этого же звена можно определить, построив на плане скоростей фигуру, подобную фигуре, образованной этими же буквами на звене механизма). Точки С, В , D на звене 3 лежат на одной прямой. На плане строим отрезок сd, соблюдая условие подобия:
Группа Ассура второго класса 3-го вида (звенья 4,5) :
где D5 — точка, находящаяся на звене 5 под точкой D. После определения скорости движения точки D5 относительно точки E можно вычислить угловую скорость звеньев 4 и 5 (ω4=ω5, т. к. эти звенья соединяются поступательной парой):
Примечание: в данном случае размер DE является величиной переменной (т.е. в задании он отсутствует), поэтому в каждом положении механизма он определяется через отрезок на чертеже и масштаб длин.
План ускорений строится в таком же порядке.
Видео:План скоростей шарнирного трехзвенного механизмаСкачать

Начальный механизм
Ускорение точки A состоит только из нормальной составляющей, т.к. задана постоянная угловая скорость первого звена (ω1=соnst):
По вычисленному значению ускорения точки A выбирается масштаб плана ускорений и определяется отрезок на плане, соответствующий этому ускорению (или вычисляется масштаб плана ускорений по выбранному отрезку, изображающему ускорение точки A):
Здесь точка w – полюс плана ускорений.
Группа Ассура (звенья 2,3) второго класса 1-го вида:
После построения определяются aτBA и aτBC, по которым можно вычислить угловые ускорения звеньев 2 и 3:
Ускорение точки D определяем по подобию так же, как определяли скорость этой точки:
Рисунок 5 – Планы скоростей и ускорений для заданного положения механизма
Группа Ассура (звенья 4,5) второго класса 3-го вида:
Для определения направления akD5D надо вектор VD5D повернуть на 90° в направлении ω5. Угловые ускорения:
- При силовом расчете необходимо иметь ускорения центров масс (asi), которые на плане ускорений определяются методом подобия.
- Планы скоростей и ускорений для первого положения заданного механизма приведены на рисунке 5.
- Уравнение планов скоростей и ускорений для каждой группы Ассура приведены в таблице 1.
- Таблица 1 – Кинематический анализ групп Ассура II класса методом планов
| Вид группы | Уравнения для построения планов скоростей и для определения угловых скоростей | Уравнения для построения планов ускорений и для определения угловых ускорений |
| 2 | ||
| 3 | ||
| 4 | ||
| 5 |
Пример расчета механизма с поступательно движущимся выходным звеном >
Курсовой проект по ТММ >
Видео:ТММ - 6.1, 6.2 Построение плана скоростей. Графоаналитический метод кинематического анализа.Скачать

Кинематический расчет механизма
Кинематический расчет механизма.
Построение траектории движения точки
Чтобы получить траекторию движения точки D, необходимо построить 12 планов положений механизма. План положений — графическое изображение положения всех звеньев механизма в определенный момент времени.
Планы положений следует сроить в верхнем левом углу листа, расположив их длинной стороной горизонтально. Масштаб следует выбирать таким, чтобы планы положений заняли 1/4 часть листа. Выбираем произвольную точку О1, и проводим через нее вертикальную и горизонтальную оси.
На горизонтальной оси находим центр вращения О2 звена 3, отложив отрезок О1 О2 (рис. 1.11а)
Радиусом О, А проводим из центра О, окружность, по которой движется точка А при вращении кривошипа. Полученную окружность делим на 12 равных частей, обозначив точки 0, 1,2, 3, … Нулевая точка должна находиться на вертикальной оси вверху.
Радиусом О2В из точки О2 проводим дугу, по которой перемещается точка В при качательных движениях звена 3. Дуга должна охватывать угол около 120° симметрично вертикали.
Для построения n-ого положения механизма, например 10-ого, радиусом АВ. из 10-ого положения точки А делаем засечку на дуге, по которой перемещается точка В. Полученные точки А и В соединяем прямой и продолжаем ее на величину BD ; Получена точка D. Точку В соединяем с точкой О2 . План 10-ого положения механизма построен.
Аналогично методом засечек строятся остальные одиннадцать положений. Соединяя все положения точки D плавной кривой, получим траекторию ее движения.
Определение степени подвижности механизма
Степень подвижности механизма определяется по формуле Чебышева П. Л.:
где n — число подвижных звеньев; Р2 — число кинематических пар второго класса; Р1 — число кинематических пар первого класса.
В рассматриваемом четырехзвённом механизме (рис 1.11а) число подвижных звеньев n =3.
На схеме механизма подвижные звенья пронумерованы от 1 до 3. стойка обозначена через 4.
Подсчитаем число кинематических пар второго класса. Имеем 4 вращательные кинематические пары в шарнирах О1А, ВО2. Следовательно Р2 = 4.
Кинематических пар первого класса в данном механизме нет, так что Pi = 0. Следовательно, имеем:
W = З×З — 2×4 — 0 = 1.
Механизмы, в состав которых входят кинематические пары только второго класса, (т. е. низшие пары), называются стержневыми. Это значит, что при наличии одного ведущего звена (кривошипа О1А) движение всех остальных звеньев будет вполне определенным.
Построение плана скоростей для заданного положения механизма
Заданы размеры звеньев О1А, АВ и ВО2 , их положения и угловая скорость ω1=const кривошипа О1А.
Определение скоростей следует начинать с ведущего звена — кривошипа О1А, закон движения которого задан:
Для определения скорости точки В условно разрушаем шарнир В и рассматриваем точку В2 принадлежащей двум звеньям: шатуну АВ и коромыслу ВО2 .
На основании теоремы сложения скоростей для точки В составляем следующие векторные уравнения:

- где — скорость полюса в переносном поступательном движении;
- — скорость относительного вращательного движения вокруг полюса А;
- — скорость относительного вращательного движения вокруг полюса О2 .
- Векторы, известные по величине и направлению, условимся подчеркивать двумя чертами, а известные только по направлению — одной чертой.
Сущность метода плана скоростей состоит в графическом решении векторных уравнений (1) и (2) (рис 1.11б).
План скоростей строится в определенном масштабе. Масштаб рекомендуется выбирать следующим образом: например скорость некоторой
точки А ведущего звена =7,2 м/с. Для изображения вектора скорости точки А целесообразно выбирать отрезок, например, PVа =72 мм.
Отрезок Рva можно взять любой величины, но лучше выбрать его таким, чтобы масштаб скоростей был удобным для дальнейших вычислений. Отрезок Pv a следует выбирать в пределах (70…120)мм.
Построение плана скоростей проводим в следующем порядке. (рис 1.11 б):
- 1) откладываем от произвольного полюса (Pv) отрезок, PVa ׀׀
- VA
- 2) через конец (а) отрезка ( Pva) проводим направление скорости перпендикулярно шатуну АВ механизма;
3) из полюса (РV) проводим направление скорости т. е. линию, перпендикулярную звену ВО2, до пересечения с направлением . Точка пересечения (b) этих двух направлений определяет величины скоростей и :
- Направления векторов полученного треугольника нужно согласовать с уравнением (1).
- Для определения скорости точки D, лежащей на звене АВ механизма, находим ее изображение в плане скоростей методом пропорционального деления из соотношения (на основе свойства подобия плана скоростей):
- , откуда
- Продолжив (ab) и отложив (ad), получим положение точки (d). Скорость точки D получим, соединив полюс ( Pv ) с точкой (d):
- Построение плана ускорений для заданного положения механизма.
- При определении ускорений точек механизма сохраняется та же последовательность решения, что и при определении скоростей. Ускорение точки А ведущего звена О1А, равно геометрической сумме векторов нормального и тангенциального ускорений этой точки
- Так как кривошип вращается равномерно, то и, следовательно полное ускорение точки А будет состоять только из нормального:
- направленного вдоль кривошипа О1А от точки А к точке О1.
- Плоскопараллельное движение шатуна АВ, как и при определении скоростей, раскладывается на переносное поступательное движение вместе с полюсом А и относительное вращательное движение вокруг полюса А. По теореме сложения ускорений получаем:
- (3)
- Рассматривая шарнирную точку В, принадлежащей звену 3 — коромыслу ВО2 на основании теоремы сложения ускорений составляем векторное уравнение
- (4)
- После разложения векторов ускорения и на нормальные и тангенциальные составляющие уравнения (3) и (4) примут вид:
- (5)
- (6)
- Векторы, подчеркнутые дважды, известны и по величине, и по направлению. Для построения плана определяем модули:
- ;
- Нормальные ускорения всегда известны по величине и направлению, а тангенциальные — только по направлению.
- Нормальные ускорения точек направлены к центру вращения звена.
- Так, вектор параллелен звену АВ и направлен от точки В к точке
- А, вектор , параллелен звену ВО2 и направлен от точки В к точке О2.
- Вектор направлен перпендикулярно звену АВ, а вектор
— перпендикулярно звену ВО2. Величины тангенциальных ускорений определяются в результате построения плана ускорений.
Решаем уравнение (5) и (6) графически, построением плана ускорений (рис. 1.11.в).
- Выбираем масштаб плана ускорений, для чего принимаем дину отрезка , изображающего вектор ускорения точки А, равной 70-120 мм. Тогда масштаб плана ускорений:
- м/с×мм
- Построение плана ускорений следует вести в следующем порядке. Из
произвольно выбранного полюса Ра (рис. 1.11 в) проводим параллельно
- О1А, отрезок Paa направленный от точки А к точке О1. Из точки а
- проводим вектор в направлении от точки В к точке А, длина вектора равна:
- Через точку следует провести перпендикулярно звену АВ на-
правление вектора . Далее из полюса ( Pа ) проводим вектор в направлении от точки В к точке O2. Длина его равна:
- Через точку проводим перпендикулярно звену ВО2 направление вектора .
- В пересечении направлений векторов и получим точку b — конец вектора абсолютного ускорения точки В.
- Направление ускорений и должно быть согласовано с уравнениями (5) и (6). Из плана ускорений определяем:
Чтобы найти полные ускорения и нужно на плане провести замыкающие векторы, т. е. отрезки и и направить их навстречу слагаемым: ;
- Ускорение точки D определяется на основании свойства подобия плана ускорений, для чего на продолжении отрезка (ab) откладывается отрезок (bd), найденный из пропорции:
- ;
- Ускорение точки D получим, соединив полюс ( Ра) с точкой (d):
- Определение угловых скоростей и угловых ускорений звеньев.
- Величина угловой скорости звена 1 — ω1, является заданной и постоянной. Величина угловой скорости звена 2 равна относительной скорости
, деленной на длину звена АВ, т. е.
- Вектор , направлен по часовой стрелке. Ведущее звено l вращается
- с постоянной угловой скоростью, так, что его угловое ускорение.
- Величина углового ускорения звена 2 равна тангенциальному ускорению , деленному на длину звена АВ :
вектор направлен против часовой стрелки. Так как векторы угловой скорости , и углового ускорения звена 2 имеют разное направление, то звено 2 — шатун — в этом положении движется замедленно.
- Подобным образом находим угловую скорость и угловое ускорение звена 3.
- Движение звена 3 в данном положении ускоренное, так как векторы
- и имеют одинаковое направление.
Видео:#Построение плана скоростей кулисного механизма-практика (КП)Скачать

Кинематика — Физика — Теория, тесты, формулы и задачи — Обучение Физике, Онлайн подготовка к ЦТ и ЕГЭ
Основные теоретические сведения
Система СИ
Основные единицы измерения величин в системе СИ таковы:
- единица измерения длины — метр (1 м),
- времени — секунда (1 с),
- массы — килограмм (1 кг),
- количества вещества — моль (1 моль),
- температуры — кельвин (1 К),
- силы электрического тока — ампер (1 А),
- Справочно: силы света — кандела (1 кд, фактически не используется при решении школьных задач).
При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок.
Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
Таблица дольных и кратных приставок в физике:
Путь и перемещение
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела.
Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой.
Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета.
Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:
где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
Средняя скорость
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:
где: Lполн – весь путь, который прошло тело, tполн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
- При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
- И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Равноускоренное прямолинейное движение
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:
где: v0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t).
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:
Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:
В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
- Координата при равноускоренном движении изменяется по закону:
- Проекция скорости при равноускоренном движении изменяется по такому закону:
- Аналогичные формулы получаются для остальных координатных осей. Формула для тормозного пути тела:
Свободное падение по вертикали
На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли.
Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением.
Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:
Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением.
Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали.
Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х» писать «у». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
- Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:
- Время падения тела с высоты h без начальной скорости:
- Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Горизонтальный бросок
При горизонтальном броске с начальной скоростью v0 движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.
Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна vx = v0. А вертикальная возрастает по законам ускоренного движения vy = gt. При этом полная скорость тела может быть найдена по формулам:
- При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:
- Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:
- Угол между горизонтом и скоростью тела легко найти из соотношения:
- Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали. Тогда этот угол будет находиться из соотношения:
Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:
- Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:
При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:
Бросок под углом к горизонту (с земли на землю)
- Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
- Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):
- Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:
Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Сложение скоростей
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны.
Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными.
Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны. Классический закон сложения скоростей:
Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Равномерное движение по окружности
Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.
Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:
Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:
- В обеих формулах: N – количество оборотов за время t. Как видно из вышеприведенных формул, период и частота величины взаимообратные:
- При равномерном вращении скорость тела будет определяется следующим образом:
где: l – длина окружности или путь, пройденный телом за время равное периоду T. При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах.
Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt.
Очевидно, что за время равное периоду T тело пройдет угол равный 2π, следовательно при равномерном движении по окружности выполняются формулы:
Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:
- Связь между модулем линейной скорости v и угловой скоростью ω:
При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
- Модуль центростремительного ускорения связан с линейной v и угловой ω скоростями соотношениями:
- Обратите внимание, что если тела (точки) находятся на вращающемся диске, шаре, стержне и так далее, одним словом на одном и том же вращающемся объекте, то у всех тел одинаковые период вращения, угловая скорость и частота.
Видео:План скоростей кривошипно-ползунного механизмаСкачать

Сложное движение точки. Теорема Кориолиса
Определение сложного (составного) движения точки. Определение абсолютного, относительного и переносного движения, скорости и ускорения. Доказательство теоремы о сложении скоростей и теоремы Кориолиса о сложении ускорений. Кориолисово (поворотное) ускорение.
Здесь мы покажем, что при сложном движении, абсолютная скорость точки равна векторной сумме относительной и переносной скоростей: . Абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений: , где – кориолисово ускорение.
Пример применения изложенной ниже теории приводится на странице “Сложное движение точки. Пример решения задачи”.
Сложное (составное) движение точки
Часто встречаются случаи, когда точка совершает известное движение относительно некоторого твердого тела. А это тело, в свою очередь, движется относительно неподвижной системы координат.
Причем движение точки относительно тела и закон движения тела относительно неподвижной системы координат известны или заданы.
Требуется найти кинематические величины (скорость и ускорение) точки относительно неподвижной системы координат.
Такое движение точки называется сложным или составным.
Сложное или составное движение точки – это движение в подвижной системе координат. То есть движение точки описывается в системе координат, которая сама совершает движение относительно неподвижной системы координат.
Далее, для ясности изложения, будем считать, что подвижная система координат жестко связана с некоторым твердым телом. Мы будем рассматривать движение точки относительно тела (относительное движение) и движение тела относительно неподвижной системы координат (переносное движение).
Относительное движение точки при сложном движении – это движение точки относительно тела (подвижной системы координат) считая, что тело покоится. Переносное движение точки при сложном движении – это движение точки, жестко связанной телом, вызванное движением тела. Абсолютное движение точки при сложном движении – это движение точки относительно неподвижной системы координат, вызванное движением тела и движением точки относительно тела.
Сложное движение. Точка M движется относительно движущегося тела.
Пусть Oxyz – неподвижная система координат, On xo yo zo – подвижная система координат, жестко связанная с телом.
Пусть – единичные векторы (орты), направленные вдоль осей xo , yo , zo подвижной системы координат.
Тогда радиус-вектор точки M в неподвижной системе определяется по формуле: (1) , где – радиус-вектор точки On – начала подвижной системы координат, связанной с телом.
Относительная скорость и ускорение
При относительном движении изменяются координаты xo , yo , zo точки относительно тела. А векторы являются постоянными, не зависящими от времени. Дифференцируя (1) по времени, считая постоянными, получаем формулы для относительной скорости и ускорения: (2) ; (3) .
Относительная скорость точки при сложном движении – это скорость точки при неподвижном положении тела (подвижной системы координат), вызванная движением точки относительно тела. Относительное ускорение точки при сложном движении – это ускорение точки при неподвижном положении тела, вызванное движением точки относительно тела.
Переносная скорость и ускорение
При переносном движении изменяются векторы , определяющие положение тела. Относительные координаты точки xo , yo , zo являются постоянными. Дифференцируя (1) по времени, считая xo , yo , zo постоянными, получаем формулы для переносной скорости и ускорения: (4) ; (5) .
Переносная скорость точки при сложном движении – это скорость точки, жестко связанной с телом, вызванная движением тела. Переносное ускорение точки при сложном движении – это ускорение точки, жестко связанной с телом, вызванное движением тела.
Производные по времени от – это скорость и ускорение начала подвижной системы координат On : ; .
Найдем формулы для производных по времени от векторов . Для этого возьмем две произвольные точки твердого тела A и B. Их скорости связаны соотношением: (см. страницу “Скорость и ускорение точек твердого тела”). Рассмотрим вектор , проведенный из точки A в точку B. Тогда . Дифференцируем по времени и применяем предыдущую формулу:
Итак, мы нашли формулу для производной по времени от вектора, соединяющего две точки тела:
Поскольку векторы жестко связаны с телом, то их производные по времени определяются по этой формуле: (6) , , .
Подставляем в (4): . Таким образом, выражение (4) приводит к формуле для скорости точек твердого тела.
Выполняя подобные преобразования над формулой (5), получим формулу для ускорения точек твердого тела: , где – угловое ускорение тела.
Абсолютная скорость и ускорение
При абсолютном движении изменяются как векторы , определяющие положение тела, так и относительные координаты точки xo , yo , zo .
Абсолютная скорость точки при сложном движении – это скорость точки в неподвижной системе координат. Абсолютное ускорение точки при сложном движении – это ускорение точки в неподвижной системе координат.
Теорема о сложении скоростей
При составном движении абсолютная скорость точки равна векторной сумме относительной и переносной скоростей: .
Доказательство
Дифференцируем (1) по времени, применяя правила дифференцирования суммы и произведения. Затем подставляем (2) и (4). (1) ; (7) .
Теорема Кориолиса о сложении ускорений
- При составном движении абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений: , где
- – кориолисово ускорение.
Доказательство
Дифференцируем (7) по времени, применяя правила дифференцирования суммы и произведения. Затем подставляем (3) и (5). (7) . .
В последнем члене применим (6) и (2). . Тогда
Видео:Занятие 2 - Построение планов скоростейСкачать

Закон сложения скоростей
Механическим движением называют изменение положения тела в пространстве относительно других тел с течением времени.
В этом определении ключевой является фраза «относительно других тел». Каждый из нас относительно какой-либо поверхности неподвижен, но относительно Солнца мы совершаем вместе со всей Землей орбитальное движение со скоростью 30 км/с, то есть движение зависит от системы отсчета.
Система отсчета – совокупность системы координат и часов, связанных с телом, относительно которого изучается движение.
Например, описывая движения пассажиров в салоне автомобиля, систему отсчета можно связать с придорожным кафе, а можно с салоном автомобиля или с движущимся встречным автомобилем, если мы оцениваем время обгона
Преобразование координат и времени
Закон сложения скоростей является следствием преобразований координат и времени.
Пусть частица в момент времени t’ находится в точке (x’, y’, z’), а через малое время Δt’ в точке (x’ + Δx’, y’ + Δy’, z’ + Δz’) системы отсчета K’. Это два события в истории движущейся частицы. Имеем:
- Δx’ = vx’Δt’,
- где vx’ — x-я компонента скорости частицы в системе K’.
- Аналогичные соотношения имеют место для остальных компонент.
- Разности координат и промежутки времени (Δx, Δy, Δz, Δt) преобразуются так же, как координаты:
- Δx = Δx’ + VΔt’,
- Δy = Δу’,
- Δz = Δz’,
- Δt = Δt’.
- Отсюда следует, что скорость той же частицы в системе K будет иметь компоненты:
- vx = Δx / Δt = (Δx’ + VΔt’) / Δt = vx’ + V,
- vy = vy’,
- vz = vz’.
- Это закон сложения скоростей. Его можно выразить в векторной форме:
- v̅ = v̅’ + V
- (координатные оси в системах K и K’ параллельны).
- Если тело движется относительно системы отсчета К1 со скоростью V1, а сама система отсчета К1 движется относительно другой системы отсчета К2 со скоростью V, то скорость тела (V2) относительно второй системы отсчета К2 равна геометрической сумме векторов V1 и V.
- Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета.
- ( vec = vec + vec )
где всегда К2 — неподвижная система отсчетаV2 — скорость тела относительно неподвижной системы отсчета (К2)
К1 — подвижная система отсчета
V1 — скорость тела относительно подвижной системы отсчета (К1)
V — скорость подвижной системы отсчета (К1) относительно неподвижной системы отсчета (К2)
Закон сложения ускорений для поступательного движения
В общем случае, когда движение материальной точки (тела) является криволинейным, его в каждый момент времени можно представить как комбинацию поступательного движения материальной точки (тела) относительно подвижной системы отсчёта со скоростью ( <overrightarrow>_r ), и вращательного движения подвижной системы отсчёта относительно неподвижной с угловой скоростью ( <overrightarrow>_e ). В этом случае, при сложении ускорений, наряду с относительным и переносным ускорением необходимо учитывать и ускорение Кориолиса ( a_c=2<overrightarrow>_e imes <overrightarrow>_r ), которое характеризует изменение относительной скорости, вызванное переносным движением, и изменение переносной скорости, вызванное относительным движением.
Теорема Кориолиса
- Вектор ускорения материальной точки (тела) относительно неподвижной системы отсчёта ( overrightarrow=frac<doverrightarrow>
- = _ ) (абсолютное ускорение) является суммой вектора ускорения тела относительно подвижной системы отсчета ( _r=frac<d<overrightarrow>_r>
- =_ ) (относительного ускорения), вектора ускорения подвижной системы отсчёта относительно неподвижной ( _е=frac<d<overrightarrow>_е>
- =_ ) (переносного ускорения), и кориолисова ускорения ( a_c=2<overrightarrow<>>_e imes <overrightarrow>_r=_ ):
- = _ ) (абсолютное ускорение) является суммой вектора ускорения тела относительно подвижной системы отсчета ( _r=frac<d<overrightarrow>_r>
- [_=_+_+_]
- Абсолютное перемещение равно сумме относительного и переносного перемещений.
- Перемещение тела в неподвижной системе отсчета равно сумме перемещений: тела в подвижной системе отсчета и самой подвижной системы отсчета относительно неподвижной.
Вторая капля оторвалась от крыши через несколько секунд после того, как оторвалась первая капля. Как движется вторая капля относительно первой? Сопротивлением воздуха пренебречь.
За неподвижную систему отсчёта возьмём землю, за подвижную систему отсчёта — первую каплю, а за наблюдаемое тело — вторую каплю. Отметим, что подвижная система отсчета движется поступательно.
Поскольку сопротивлением воздуха пренебрегаем, то на каждую из капель будет действовать лишь одна сила тяжести, сообщающая каждой капле ускорение (относительно земли), равное ускорению свободного падения g.
Следовательно, абсолютное ускорение (ускорение второй капли относительно земли) равно g, и переносное ускорение (ускорение первой капли относительно земли) также равно g. По закону сложения ускорений, относительное ускорение (ускорение второй капли относительно первой) равно нулю, значит, вторая капля движется равномерно относительно первой.
вторая капля движется относительно первой равномерно.
Жесткий диск вращается с постоянной угловой скоростью $overrightarrow<>$ вокруг оси, укрепленной на столе. По диску движется точка А с постоянной относительно стола скоростью $overrightarrow$.
- Относительная скорость точки А $ <overrightarrow>_r=overrightarrow-<overrightarrow<>>_e imes overrightarrow <<mathbf
ho >>$. - Поскольку скорость точки $overrightarrow$ относительно стола постоянна, то её абсолютное движение равномерно, и $overrightarrow=0$
- Отсюда
Запишите теорему сложения ускорений для поступательного движения материальной точки.
тогда в любой момент времени равно нулю ускорение Кориолиса. Теорема сложения ускорений принимает вид:
- Абсолютная скорость мухи, ползущей по радиусу вращающейся граммофонной пластинки, равна сумме скорости её движения относительно пластинки и той скорости, с которой её переносит пластинка за счёт своего вращения.
- Если человек идёт по коридору вагона со скоростью 5 километров в час относительно вагона, а вагон движется со скоростью 50 километров в час относительно Земли, то человек движется относительно Земли со скоростью 50 + 5 = 55 километров в час, когда идёт по направлению движения поезда, и со скоростью 50 — 5 = 45 километров в час, когда он идёт в обратном направлении.
- Если человек в коридоре вагона движется относительно Земли со скоростью 55 километров в час, а поезд со скоростью 50 километров в час, то скорость человека относительно поезда 55 — 50 = 5 километров в час.
- Если волны движутся относительно берега со скоростью 30 километров в час, а корабль также со скоростью 30 километров в час, то волны движутся относительно корабля со скоростью 30 — 30 = 0 километров в час, то есть они становятся неподвижными.
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
- В инерциальной системе отсчета тело движется равномерно и прямолинейно при отсутствии действующих на него сил.
- Ускорение, приобретенное телом в инерциальной системе отсчета, прямо пропорционально равнодействующей силе и обратно пропорционально массе тела.
- Все ИСО по своим механическим свойствам эквивалентны друг другу.
- Второй закон термодинамикиНевозможно создать круговой процесс, результатом которого станет исключительно превращение теплоты, которое получено от нагревателя, в работу.
- Лошадиная сила — единица мощности. Она примерно равна значению в 75 кгс/м/с., что соответствует усилию, которое необходимо затратить для подъёма груза в 75 кг. на высоту одно метра за одну секунду.
- Сколько должен весить человек?Чтобы узнать вес человека, достаточно знать его рост в сантиметрах, из этой цифры вычесть 100, а к полученному числу либо прибавить 10, если речь идет о мужчине, либо отнять 10, если вычисляется вес женщины.
- Ведро́ — сосуд для хранения жидких и сыпучих материалов и транспортировки их на небольшие расстояния.
- Закон всемирного тяготенияМежду любыми материальными точками существует сила взаимного притяжения, прямо пропорциональная произведению их масс и обратно пропорциональная квадрату расстояния между ними, действующая по линии, соединяющей эти точки
🎬 Видео
ПРАКТИКА # 6.ТММ. ПЛАН СКОРОСТЕЙ.Скачать

⚙️Установка Шаговых Моторов на Координатный СтоликСкачать

КОМПАС-3D v17: План скоростей ТММ (теория механизмов и машин)Скачать

Курсач ТММ часть 1Скачать

План скоростей кулисного механизмаСкачать

ТММ - 7 1, 7 2 Построение планов скоростей. Лекция-практикаСкачать

План ускорений кривошипно-ползунного механизмаСкачать

Инверсный планетарный редуктор, прецессирующий редуктор - объяснение большого передаточного числаСкачать

01 Решение для векторных уравнений для семестровых и курсовых по ТММСкачать

03 Построение плана скоростей механизмаСкачать

План скоростей и план ускорений. Задача 2Скачать

Построение плана ускорений. ТММСкачать