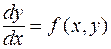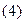Видео:Составить дифференциальные уравнения семейств линийСкачать

Составление уравнений семейства кривых
Чтобы построить дифференциальное уравнение, которому удовлетворяют кривые семейства:
φ 
необходимо продифференцировать равенство (1) n раз, считая y функцией от x, а затем из полученных уравнений и уравнения (1) исключить произвольные постоянные C1 … Cn.
Линии, пересекающие все кривые данного семейства под одним и тем же углом ϕ, называются изогональными траекториями . Углы β и α наклона траектории и кривой к оси Ox связаны соотношением β = α ± φ.


Тогда tg α = f (x,y), tg β = f1 (x,y).
Отсюда следует, что если дифференциальное уравнение семейства кривых написано и угол φ известен, то найти tg β не составит труда, а после также легко можно будет написать уравнение траекторий.
Частный случай:
Если уравнение семейства кривых записано в виде:

то при составлении уравнения траекторий можно обойтись без решения уравнения относительно y’, в этом случае будет достаточно y’ заменить на tg α = tg (β ± φ), где tg β = y’ — угловой коэффициент касательной к траектории.
Пример №1
Составить дифференциальное уравнение семейства кривых:
- Так как уравнение содержит два параметра (С1 и С2), то и дифференцировать будем два раза:
Первая производная:
Вторая производная:
- Дальше, чтобы составить дифференциальное уравнение семейства кривых необходимо избавиться от С1 , а для этого выведем его из уравнения первой производной С1 = -2(y — С2)y’ и подставим в наше уравнение:

- Теперь также нужно избавиться от параметра C2, а для этого выведем ее из второй производной: y — C2 = -y’ 2 / y» и подставим это в (2):
- Ну и наконец упростим полученное уравнение и получим:
Пример №2
Для закрепления составим еще одно уравнение:
Решение абсолютно идентично предыдущему, за исключением того, что вместо параметров С1 и С2 здесь представлены параметры a, b и с. Ну и, конечно, раз параметров три, то нам понадобятся производные первого, второго и третьего порядка.
Делать описание каждого шага я уже не буду, думаю вы уже сами разберетесь:
Первая производная:
Вторая производная:
Третья производная:
Ответ:
Ну, думаю, если вы разобрались в первыми двумя примерами, то все остальные вы решите без труда, а чтобы это проверить дам вам парочку заданий «на дом».
Пример №3
Выразим коэффициенты a и b через 1-ую и 2-ую производные:
Первая производная: 
Вторая производная: 
Подставим значение b второй производной в значение a первой производной:
А теперь подставим полученные значения a и b в исходное уравнение и упростим:

Ответ:
Пример №4
Ну а здесь все еще проще:
Возведем обе части уравнения в квадрат:
Чтобы воспользоваться основным тригонометрическим тождеством, вычтем из единицы обе части уравнения:
Ну и теперь как мы видим во второй части получилось исходное уравнение, только в квадрате, а значит оно будет равно:
Приведем к общему виду и запишем ответ:
Ответ:
Ну и на этой ноте мы с вами закончим данный урок, всем спасибо!
Если вам что-то непонятно (или нашли неточности в уроке) пишите в комментариях и мы вам обязательно ответим в ближайшее время.
Видео:Составить дифференциальное уравнение семейства кривыхСкачать

Составление дифференциальных уравнений семейств линий
Пусть дано уравнение однопараметрического семейства плоских кривых
Дифференцируя (1) по , найдем
Исключая параметр из (1) и (2), получаем дифференциальное уравнение
выражающее свойство, общее всем кривым семейства (1). Уравнение (3) будет искомым дифференциальным уравнением семейства (1).
Если однопараметрическое семейство кривых определяется уравнением
то дифференциальное уравнение этого семейства получим, исключая параметр из уравнений
Пусть теперь имеем соотношение
где — параметры. Дифференцируя (4) раз по и исключая параметры из (4) и полученных уравнений, приходим к соотношению вида
Это дифференциальное уравнение заданного n-параметрического семейства линий (4) в том смысле, что (4) есть общий интеграл уравнения (5).
Пример 1. Найти дифференциальное уравнение семейства гипербол .
Решение. Дифференцируя это уравнение по , получаем
Умножим обе части на , тогда . Подставляя в уравнение семейства найдем .
Пример 2. Найти дифференциальное уравнение семейства линий , где — параметр.
Решение. Дифференцируем обе части уравнения по :
Из выражения для находим
и, подставляя это выражение для в уравнение семейства линий, получим
Пример 3. Составить дифференциальное уравнение семейства прямых, отстоящих от начала координат на расстояние, равное единице.
Решение. Будем исходить из нормального уравнения прямой
Дифференцируя (6) по , найдем , откуда , следовательно,
Подставив и в (6), получим
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

2°. Задачи на траектории
Пусть дано семейство плоских кривых, зависящее от одного параметра ,
Кривая, образующая в каждой своей точке постоянный угол с проходящей через эту точку кривой семейства (7), называется изогональной траекторией этого семейства; если, в частности, , то — ортогональной траекторией .
Считая семейство (7) заданным, будем разыскивать его изогональные траектории.
А. Ортогональные траектории . Составляем дифференциальное уравнение данного семейства кривых (см. п. 1). Пусть оно имеет вид
Дифференциальное уравнение ортогональных траекторий имеет вид
Общий интеграл этого уравнения дает семейство ортогональных траекторий.
Пусть семейство плоских кривых задано уравнением в полярных координатах
получаем дифференциальное уравнение семейства ортогональных траекторий
Б. Изогональные траектории . Пусть траектории пересекают кривые данного семейства под углом , причем . Можно показать, что дифференциальное уравнение изогональных траекторий имеет вид
Пример 4. Найти ортогональные траектории семейства линий .
Решение. Семейство линий состоит из прямых, проходящих через начало координат. Для нахождения дифференциального уравнения данного семейства дифференцируем по обе части уравнения . Имеем . Исключая параметр из системы уравнений будем иметь дифференциальное уравнение семейства . Заменяя в нем на , получаем дифференциальное уравнение ортогональных траекторий , или . Полученное уравнение является уравнением с разделяющимися переменными; интегрируя его, найдем уравнение ортогональных траекторий . Ортогональными траекториями являются окружности с центром в начале координат (рис. 15).
Пример 5. Найти уравнение семейства линий, ортогональных к семейству .
Решение. Данное семейство линий представляет собой семейство окружностей, центры которых находятся на оси и которые касаются оси .
Дифференцируя по обе части уравнения данного семейства, найдем . Исключая параметр из уравнений получаем дифференциальное уравнение данного семейства . Дифференциальное уравнение ортогональных траекторий есть
Это уравнение является однородным. Интегрируя его, найдем . Интегральные кривые являются окружностями, центры которых расположены на оси и которые касаются оси (рис. 16).
Пример 6. Найти ортогональные траектории семейства парабол .
Решение. Составляем дифференциальное уравнение семейства парабол. Для этого дифференцируем обе части данного уравнения по . Исключая параметр , найдем , или дифференциальное уравнение данного семейства. Заменяя в уравнении на , получим дифференциальное уравнение ортогональных траекторий
Интегрируя, найдем или 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAJUAAAAuBAMAAADTgUbKAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAmsOBAetBIBAxYUJRcbGvhmSvAAACYklEQVRIx2NgGOTgoNIEahnFrsEYQC2z2L6xfaOaHxN4vlMvwJgEqGfWReoZxSXQQZU4nMAxgWEygyUVjOJQVFz3kD3+/wcqmOU3IV8l3iMtLYEKZiUy5K/Qolq42xdQzSgWVQfcgWlMkte5OT4ylOGS7KsJJsUs+TN/GaxxSV4tsCfFLKEiZV+c+Wdew3osgeKC0xuSjfiiUQgzDBfFa3MtQBXzTiEmNMMxhI7qODTJo5acPIGi2OOIC5lT1IAuzfgXmO2+okZ96QGucOylD5I6DglmdMPuGwBDTA/I4BSHB6A8A8tHgmY1CZuie/oriNQFEUlww4IccCRSqFnsjyYwnFmkpIgm6/QLREJM2acNUcryyYFFH59ZfUUKLIGwYikNDEABPv8HktJCiGGcILMa8Jh1y/UB51+oEKcxGBwABZcCklKXwiiQYrZPDAz6GxgYFgrCAcjhXMbGpkBdQEtWnF/A+xNLQQBK1xxwbrEOKAwJmcUg38AUgsUsA5DT4SVLM8gsDkLhxRDE4P8Aix9B7poIDzAtkGIWQvHI8pkh/wIs7HeDASjs64H1O4c6zCgd4tIXMBLfY2lj8H50YJgEFd8ITRMM+xNwVPswPy4VCsXm7qWBRlBnJUnDs13s1QXw0tMci1ke2wOxFsN7j0MDURwhWLUcxpq0Vn8BRt4uVWAmp4kRydCKmZLyDfYvIKPi/t/A/BlDlFHpGTk1d2gD8ydMYReyajUXBsbP1GvmtEZQzyxRqrV8GbgiqeesqRM4qWUUpwYi51PsrGNpwlQyikP///8/1PKikpKSJuXGAACuZpWkdXHGfwAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />. Ортогональным семейством является семейство эллипсов (рис. 17).
Пример 7. Найти ортогональные траектории семейства лемнискат .
Решение. Имеем . Исключая параметр , получим дифференциальное уравнение данного семейства кривых Заменяя на , найдем дифференциальное уравнение семейства ортогональных траекторий откуда . Интегрируя, находим уравнение ортогональных траекторий
Ортогональными траекториями семейства лемнискат являются лемнискаты, ось симметрии которых образуют с полярной осью угол (рис. 18).
Видео:Семейство кривыхСкачать

ГЛАВА 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Дифференциальные уравнения первого порядка
Основные понятия и теоретические сведения
Рассмотрим необходимые теоретические сведения, а также параллельно изложим методы решения ряда типовых задач, разбор которых окажет студенту-заочнику существенную методическую помощь при выполнении контрольной работы.
Напомним, что уравнения вида
F (x, y, 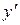
где x — независимая переменная, y — искомая функция от x, 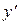

Если уравнение (1) можно разрешить относительно 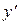
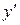
и называется уравнением первого порядка, разрешенным относительно производной. В некоторых случаях уравнение (2) удобно записать в виде
или в такой форме 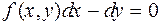
где P(x, y) и Q(x, y) — известные функции. Функция y = y(x) , заданная на интервале (a, b), называется решением уравнения (1) или (2), если при подстановке в уравнение его обращает в тождество относительно xÎ(a, b). График решения дифференциального уравнения называется интегральной кривой.
Ответ на вопрос о том, при каких условиях уравнение (2) имеет решение, дает теорема Коши.
Т е о р е м а Коши (существования и единственности решения).
Пусть правая часть f (x, y) уравнения (2) определена в некоторой области D на плоскости OХY . Если существует такая окрестность 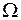
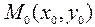
1. Непрерывна по совокупности аргументов;
2. Имеет ограниченную частную производную 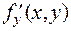
то существует и причем единственное решение y = y (x) уравнения (2) в некоторой окрестности точки 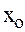
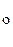

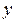
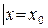
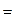

Замечание. Если в теореме требование ограниченности производной 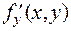
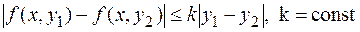
Геометрически теорема означает, что через точку M 
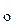
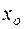
Отыскание решения уравнения (2), удовлетворяющего начальному условию (4), называется задачей Коши. С геометрической точки зрения решить задачу Коши означает: выделить из множества интегральных кривых ту, которая проходит через заданную точку M 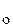
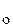
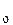
Напомним понятие общего решения. Пусть D — некоторая область на плоскости охy, через каждую точку которой проходит единственная интегральная кривая уравнения (2). Однопараметрическое семейство функций y = j (x, C ) параметра С называется общим решением уравнения (2), удовлетворяющего условиям теоремы Коши в области D, если при любом допустимом значении параметра C определяет решение этого уравнения и, кроме того, для любой внутренней точки M 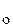
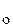
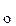
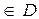
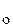
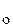
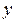
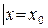
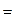

Любая функция, выделенная из общего решения, называется частным решением.
Уравнение Ф (x, y, С) = О , определяющее общее решение как неявную функцию, называется общим интегралом дифференциального уравнения.
Остановимся на следующих полезных упражнениях:
1. Рассмотрим уравнение 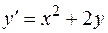

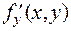
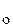
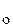
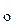
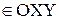
2. Дано уравнение 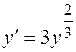
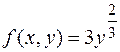
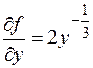
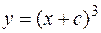
y = 0, 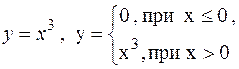
При этом через каждую точку 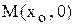
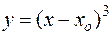
Если же взять точку 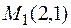
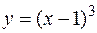
Теорема 1 дает лишь достаточные условия единственности решения уравнения (2). Однако, не исключается возможность существования единственного решения y = y (x), удовлетворяющего начальному условию 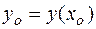
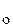
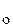
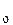
Таким образом, мы вплотную подошли к необходимости рассмотрения так называемых особых решений дифференциальных уравнений (1) или (2).
2. Особые решения
Решение дифференциального уравнения первого порядка называется особым, если соответствующая интегральная кривая обладает тем свойством, что через каждую ее точку проходит, кроме нее, еще и другая касающаяся ее интегральная кривая данного уравнения.
Итак, особое решение уравнения (2) представляет такое решение, в каждой точке которого нарушается единственность решения задачи Коши.
Отсюда следует, что для существования особого решения уравнения (2) необходимо, чтобы не выполнялось хотя бы одно из условий теоремы 1.
В частности, для уравнения 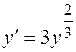
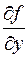
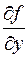
Замечание.Заметим, что особое решение не выделяется из общего решения (общего интеграла) при определенном значении параметра С.
Однако, не всякая кривая, в точках которой не выполнено условие ограниченности производной 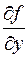
Например, для уравнения 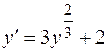
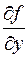
Таким образом, вышеприведенные рассуждения позволяют резюмировать для уравнения (2) при выполнении первого условия теоремы 1 следующее заключение; то есть, особые решения могут быть выявлены так:
1. Найти геометрическое место точек, в которых производная
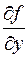
2. Если такие кривые окажутся, то проверить являются ли они интегральными кривыми уравнения (2).
3. Среди выявленных интегральных кривых проверить: нарушается ли в каждой из точек этих кривых свойство единственности.
При выполнении всех этих условий найденные кривые представляют особые решения уравнения (2).
Кроме того, следует подчеркнуть, что уравнение (2) может иметь решения, которые не являются ни частными, ни особыми. Таким примером является решение 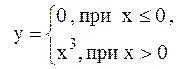
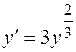
Если в любой окрестности точки M 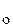
Итак, прежде всего особое решение представляет интегральную кривую, состоящую из особых точек.
Пусть общее решение уравнения (2) допускает однопараметрическое семейство интегральных кривых Ф(x,y,C) = 0, где С – параметр. Допустим, что семейство кривых имеет огибающую, т.е., кривую, которая касается каждой кривой этого семейства и причем состоит полностью из этих точек касания. При этом заметим, что огибающая семейства интегральных кривых является особым решением уравнения (2).
Огибающая семейства интегральных кривых Ф(x,y,C) = 0 определяется из следующей системы уравнений
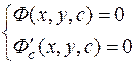
Второе уравнение системы составляется путем дифференцирования по параметру С первого уравнения. Находят кривую путем исключения параметра С из этой системы, если это возможно. Эта кривая называется дискриминантной. Затем найденную дискриминатную кривую проверяют, является ли она решением данного уравнения.
Таким образом, мы привели еще один весьма эффективный способ нахождения особых решений при помощи огибающих семейства интегральных кривых уравнения (2).
💡 Видео
Огибающая семейства кривых | Дифференциальные уравненияСкачать

2. Дифференциальное уравнение семейства кривыхСкачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

Особые решения дифференциальных уравнений, огибающая семейства кривых | Лекция 34 | МатанализСкачать

1. Что такое дифференциальное уравнение?Скачать

Решить дифф. уравнение и построить интегральные кривыеСкачать

Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

11. Уравнения в полных дифференциалахСкачать

Практика 1 ИзоклиныСкачать

Математика без Ху!ни. Уравнение касательной.Скачать

1202.Дифференциальные уравненияСкачать

Поле направлений дифференциального уравнения первого порядкаСкачать

Траектория и уравнения движения точки. Задача 1Скачать

Решение физических задач с помощью дифференциальных уравненийСкачать