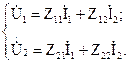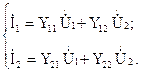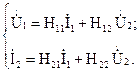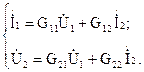В уравнениях четырехполюсника формы в коэффициенты имеют следующие размерности (8 видео)

Уравнения четырехполюсника

Зависимости между двумя напряжениями и двумя токами, определяющими режим на первичных и вторичных выводах, могут быть записаны в различных формах. Если считать две из указанных величин заданными, то две другие величины будут связаны с ними системой из двух уравнений, которые называются уравнениями четырехполюсника. Существует несколько форм записи уравнений четырехполюсника.

В том случае, если на входные зажимы четырехполюсника подается напряжение источника питания, а к выходным зажимам подключается нагрузка, то такое включение четырехполюсника называется прямым (рис. 5.2, а). Если же напряжение источника подается на выходные зажимы четырехполюсника, а нагрузка подключается к входным, то такое включение называется обратным (рис. 5.1, б). Положительные направления токов и напряжений при прямом и обратном включении

В уравнениях четырехполюсника формы в коэффициенты имеют следующие размерности

показаны на рис. 2.1.

При прямом включении четырехполюсника входные напряжение и ток можно связать с выходными напряжением и током уравнениями четырехполюсника в А-форме (5.1). При обратном включении можно связать выходные режимные параметры с входными с помощью уравнений в В-форме (5.2):

(5.1) (5.2)

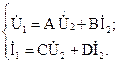
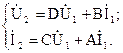
Коэффициенты А, В, С и D в этих уравнениях в общем случае являются комплексными величинами. Они зависят от внутренней структуры рассматриваемого четырехполюсника и частоты источника питания.

Коэффициенты уравнений взаимного четырехполюсника в А- и В-формах записи связаны зависимостью:

Коэффициент В имеет размерность сопротивления [Ом], коэффициент С – размерность проводимости [1/Ом], коэффициенты А и D – безразмерные.

Выражения, связывающие напряжения на входе и выходе четырехполюсника с токами, называются Z-формой записи уравнений четырехполюсника и все коэффициенты в этой системе уравнений имеют размерность сопротивлений [Ом]:

Y-формой записи называются уравнения четырехполюсника, связывающие токи на входе и выходе четырехполюсника с напряжениями на его зажимах:

Все коэффициенты этой формы записи имеют размерность проводимости [1/Ом].

Кроме этого существуют Н- и G- формы записи уравнений четырехполюсника:

Для Z, Y, Н и G – форм записи уравнений четырехполюсников принято положительное направление токов и напряжений, как показано на рис. 5.2

Видео:Задачи по четырехполюсникам. П - образная схемаСкачать

№75 Уравнения четырехполюсника.

Четырехполюсником называется часть электрической цепи или схемы, содержащая два входных вывода (полюса) для подключения источника энергии и два выходных вывода для подключения нагрузки. К четырехполюсникам можно отнести различные по назначению технические устройства: двухпроводную линию, двухобмоточный трансформатор, фильтры частот, усилители сигналов и др.

Теория четырехполюсников устанавливает связь между режимными параметрами на входе (U1, I1) и режимными параметрами на его выходе (U2, I2), при этом процессы, происходящие внутри четырехполюсника, не рассматриваются. Таким образом, единая теория четырехполюсника позволяет анализировать различные по структуре и назначению электрические цепи, которые могут быть отнесены к классу четырехполюсников.

Если четырехполюсник не содержит внутри себя источников энергии, то он называется пассивным (обозначается буквой П), если внутри четырехполюсника имеются источники, то он называется активным (обозначается буквой А).

В настоящей главе анализируются пассивные линейные четырехполюсники. На электрических схемах четырехполюсники условно обозначаются прямоугольником с двумя парами выводов: 1 и 1′ — входные выводы, 2 и 2′ — выходные выводы (рис. 75.1). Соответственно напряжение и ток на входе индексируются цифрой 1 (U1, I1) , а на выходе — цифрой 2 (U2, I2).

Установим связь между параметрами режима входа (U1, I1) и выхода (U2, I2). Для этой цели согласно теореме о компенсации заменим нагрузку Z2 источником ЭДС Е2 = U2 = I2Z2 и найдем токи по методу наложения от каждого ис¬=точника в отдельности (рис. 75.2 а, б):

где Y11, Y22 – входные проводимости входа и выхода, Y12 = Y21 – взаимная проводимость между входом и выходом.

Выразим из полученных уравнений режимные параметры на входе:

— комплексные кэффициенты четырехполюсника

С учетом принятых обозначений система основных уравнений четырехполюсника получит вид

Система основных уравнений четырехполюсника формы А:

Уравнения четырехполюсника часто записывают в матричной форме:

где матрица коэффициэнтов формы А:

Выразим соотношение между коэффициентами четырехполюсника:

A•D — B•C=1 – уравнение связи между коэффициентами. Уравнение связи показывает, что независимыми являются только три из четырех коэффициентов четырехполюсника.

Поменяем местами в схеме рис. 75.1 источник и приемник энергии. В новой схеме рис. 75.3 направления токов изменятся на противоположные.

Уравнения четырехполюсника с учетом изменения направлений токов примут вид:

Преобразуем полученную систему уравнений следующим образом. Умножим члены уравнения (1) на D, члены уравнения (2) на В и вычтем почленно из 1-го уравнения 2-ое. В результате получим:

Умножим члены уравнения (1) на С, члены уравнения (2) на А и вычтем из 1-го уравнения 2-ое. В результате получим:

Новая система уравнений четырехполюсника получила название формы В:

Четырехполюсник называется симметричным, если перемена местами входных и выходных выводов не влияет на режим остальной цепи, частью ко¬торой является четырёхполюсник. Для симметричного четырёхполюсника выполняются следующие условия:

Кроме названных форм уравнений четырехполюсника А и В применяются на практике еще четыре формы, а именно формы Z, Y, H и G. Структура этих уравнений приведена ниже:

— система основных уравнений четырехполюсника формы Z:

— система основных уравнений четырехполюсника формы Y:

— система основных уравнений четырехполюсника формы H:

— система основных уравнений четырехполюсника формы G:

Для уравнений формы Z, Y, H и G принята следующая ориентация токов и напряжений относительно выводов четырехполюсника (рис.75.4).

Соотношения между коэффициентами четырехполюсника различных форм приводятся в справочной литературе, однако их нетрудно получить, выполнив преобразование одной формы уравнений в другую. Например, пусть заданы коэффициенты формы А (А, В, С, D) и требуется определить коэффициенты формы Z(Z11, Z12, Z21, Z22). Для этого в уравнениях формы A изменим знак тока I2 и решим их относительно переменных U1 и U2:

Сравнивая полученные выражения с уравнениями четырехполюсника формы Z, находим соотношения между коэффициентами двух форм:

Видео:Классификация четырехполюсников. Системы уравнений четырехполюсниковСкачать

Четырехполюсники. Различные виды уравнений четырехполюсника. Системы параметров и их взаимосвязь. Определение коэффициентов четырехполюсников. Схемы замещения (Т — и П — образные)

Четырехполюсники. Различные виды уравнений четырехполюсника. Системы параметров и их взаимосвязь. Определение коэффициентов четырехполюсников. Схемы замещения (Т — и П — образные).

Термины и определения основных понятий

Четырехполюсник — часть электрической цепи, имеющая две пары зажимов, которые могут быть входными или выходными.

Схема замещения электрической цепи — схема электрической цепи, отображающая свойства цепи при определенных условиях.

Электрическая цепь имеющая два входных и два выходных зажима называется четырехполюсником.

Активные ЧП содержит внутри себя источники электрической энергии. Пассивные ЧП не содержит источники электрической энергии. В дальнейшем рассматриваем только пассивные ЧП.

Примерами ЧП могут служить: линия передачи, трансформатор, электрический фильтр и т. д.

Выводы ЧП к которым подключается источник электрической энергии называются входными, а выводы, к которым присоединяется нагрузка – выходными.

ЧП называется симметричным, если перемена местами его входных и выходных зажимов не изменяет напряжение и ток в остальной части цепи куда он подключен. В противном случае ЧП называется несимметричным.

На рисунке приведена в общем виде схема ЧП. Принятому положительному направлению токов соответствует передача энергии от входных зажимов к выходным зажимам.

Соотношение между напряжениями и токами могут быть записаны в виде следующих уравнений:

1.Форма || Y ||

Здесь все Y –комплексные коэффициенты пропорциональности, имеющие размерность проводимости.

При этом:

2.Форма || Z ||

Здесь все Z — комплексные коэффициенты пропорциональности, имеющие размерность сопротивления.

При этом :

3.Форма ||А||

A , D – безразмерные, В — размерность сопротивления, С – размерность проводимости.

При этом справедливо:

Наличие связи между коэффициентами, а также ;

показывает, что при любой форме записи уравнений ЧП независимыми являются только 3 параметра.

Коэффициенты зависят от схемы внутренних соединений ЧП, от величины сопротивлений схемы и частоты.

Если поменять местами вход и выход ЧП, то

Для симметричного ЧП:

A , B , C , D называются первичными параметрами ЧП.

Определение коэффициентов ЧП ( первичных параметров)

Если внутреннее содержимое ЧП известно, то его коэффициенты можно определить теоретически (расчетным путем).

1 способ. Он состоит в записи уравнений по законам Кирхгофа и последовательным приведением этих уравнений к одной из форм уравнений .

(1)

Приведем полученную систему к форме || Z ||:

Из (3): подставим с в (1) и (2)

форма ||Z||

Приведем полученную систему к форме || A ||:

Из (2)

— верно

2 способ: По известным напряжениям и токам в режимах холостого хода и короткого замыкания.

Покажем, что этим способом мы получили те же результаты:

3 способ: Если внутренне содержимое ЧП неизвестно, то коэффициенты A , B , C , D можно определить по экспериментально найденным входным сопротивлениям ЧП в режимах холостого хода и короткого замыкания.

Величина входного сопротивления могут быть легко найдена с помощью амперметра, вольтметра и ваттметра.

Для входных зажимов ЧП входное сопротивление:

При ХХ () (1)

При КЗ () (2)

Еще одно уравнение получим из уравнений для обратного включения.

Для обратного включения имеем:

В режиме ОКЗ () (3)

Решим уравнения (1)—(3) относительно какого-либо коэффициента (например А). Для этого выразим коэффициенты В, С, D и подставим полученные значения в уравнение связи.

Для симметричного ЧП A = D и

Поэтому

Для определения коэффициентов симметричного ЧП достаточно провести опыты ХХ и КЗ.

Эквивалентные схемы ЧП.

Т. К.пассивный ЧП характеризуется тремя независимыми параметрами, то его эквивалентная схема должна содержать как минимум три элемента.

На рисунке привидены Т и П-образная эквивалентные схемы.

Найдем А коэффициент Т — схемы:

Выразим Т-схемы через .

Тогда

Или

Аналогично для П-схемы имеем:

Если ЧП симметричный, то А= D и в Т — схеме , а в П — схеме

Коэффициенты A , B , C , D – называются первичными параметрами ЧП

Пассивный ЧП не содержит источников электрической энергии, активные – содержат.

Примеры ЧП: линия передачи, трансформатор, электрический фильтр и т. д.

Выводы ЧП к которым подключается источник электрической энергии называются входными, а выводы с нагрузкой – выходными.

ЧП называется симметричным если перемена местами его входных и выходных зажимов не изменяет напряжение и ток в остальной части цепи куда он подключен.

Соотношение между напряжениями и токами ЧП могут быть записаны в виде следующих уравнений:

Здесь все Y –комплексные коэффициенты пропорциональности имеющие размерность проводимости.

Здесь все Z — комплексные коэффициенты пропорциональности, имеющие размерность сопротивления.

Наличие связи (1) между коэффициентами ЧП, а также Y 12 =- Y 21 , Z 12 =- Z 21 , показывает что при любой записи элементов ЧП независимыми являются только 3 параметра.

A , B , C , D – первичные параметры ЧП.

Если поменять входное и выходное, то

Определение коэффициентов ЧП

Если внутреннее содержимое ЧП известно, то его коэффициенты можно определить аналитически.

C остоит в записи уравнений по законам Кирхгофа и последовательным приведением этих уравнений к одной из форм уравнений ЧП.

II .По известным напряжениям и токам в режимах холостого хода и короткого замыкания.

Если внутренне содержимое ЧП неизвестно, то коэффициенты A , B , C , D можно определить по экспериментально найденным входным сопротивлениям ЧП В режимах холостого хода и короткого замыкания.

Входное сопротивление R со стороны вторичных зажимов.

Если ЧП симметричен, то Z хх = Z охх , Z кз = Z окз .

Величины входных сопротивлений находятся с помощью А, В и Вг

Эквивалентные схемы ЧП.

Так как пассивный ЧП характеризуется тремя независимыми параметрами, то его эквивалентная схема должна содержать как минимум тир элемента.

Широкое распространение получили Т и П-образные схемы.

Величины входных сопротивлений находятся с помощью амперметра, вольтметра и ваттметра.