В уравнении ван дер ваальса p a2 v2 v b rt (5 видео)

В уравнении ван дер ваальса p a2 v2 v b rt

Уравнение Ван–дер–Ваальса

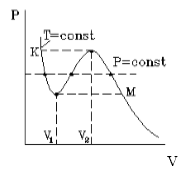
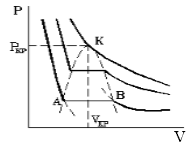
Уравнение Ван–дер–Ваальса (7.1.2) – одно из первых уравнений состояния реального газа. Данное уравнение учитывает конечные размеры всех молекул, что становится существенным при больших давлениях, а также притяжение молекул в результате межмолекулярного взаимодействия.

Уравнение состояния реального газа, предложенное Ван–дер–Ваальсом можно получить из следующих рассуждений. Учтем влияние конечных размеров молекул на уравнение состояния реального газа. Давление определяется средней кинетической энергией теплового движения всех молекул Р = nkT. 7.2.1 При конечных размерах молекул, имеющих радиус r, область 4p(2r) 3 /3 вокруг каждой из молекул будет недоступна для попадания в нее другой неточечной молекулы. В результате в сосуде, содержащем N молекул конечных размеров, область объемом (N/2)4p(2r) 3 /3 = 4NV_молек (V_молек = 4pr 3 /3 – объем одной молекулы) будет недоступна для столкновений. Поэтому можно считать, что половина всех молекул занимает объем b = 4NV_молек и покоится, а другая половина представляет собой точечные молекулы и движется с удвоенной кинетической энергией, обладая температурой Т´ = 2Т. Объем, доступный точечным молекулам, будет равен V — b, а давление, оказываемое на стенки сосуда, определяется точечными подвижными молекулами (N´ = N/2):

Р = n´kT´ =

Если в сосуде находится один моль газа, то уравнение состояния примет вид (N = N_A, N_Ak = R, b = 4N_AV_молек):

Для v = m/m молей газа уравнение состояния газа с учетом конечного размера молекул примет вид

Отметим, что это уравнение является приближенным и выведено в предположении только парных столкновений. При больших давлениях это условие уже не выполняется, и возможно одновременное соприкосновение трех и более частиц, а такие случаи были исключены из рассмотрения.

Рассмотрим теперь влияние сил притяжения на уравнение состояния идеального газа. Будем считать для простоты частицы газа точечными. Наличие сил притяжения между ними, действующих на больших расстояниях, приводит к появлению дополнительного внутреннего воздействия на газ. Это обусловлено тем, что в то время как в объеме газа действие сил притяжения между молекулами в среднем уравновешивается, на границе «газ – стенка сосуда» действие сил притяжения со стороны газа остается не скомпенсированным, и появляется избыточная сила, направленная в сторону газа (рис. 7.3).

В результате избыточное внутреннее давление P_i (i — intrinsic) будет пропорционально квадрату концентрации числа частиц

где N – полное число частиц в сосуде объема V. Если N = N_A – в сосуде находится один моль газа, то запишем

P_i = a/V 2 ,
где а – постоянная величина, своя для каждого сорта газа. В случае v-молей имеем

С учетом внутреннего давления уравнение состояния примет вид

Давление P_i не зависит от материала стенки, в противном случае удалось бы создать вечный двигатель первого рода. Роль стенки может играть и сам газ. Достаточно для этого выполнить мысленное сечение произвольной плоскостью любой внутренней области объема газа. Полученное уравнение, с учетом выражения для P_i переходит в новое уравнение состояния реального газа при наличии сил притяжения:

(P + v 2 a/V 2 )V = vRT.

Учитывая совместное действие сил притяжения и сил отталкивания и полученные поправки для объема и давления в уравнении Менделеева – Клапейрона, получим уравнение Ван–дер–Ваальса для реального газа:

(P + v 2 a/V 2 )(V — vb) = vRT, (7.2.3)

Содержание

Уравнение Ван-дер-Ваальса
Что такое реальный газ
Уравнение Ван-дер-Ваальса
Готовые работы на аналогичную тему
Уравнение Ван-дер-Ваальса
💥 Видео

Видео:Реальный газ Уравнение Ван-Дер-ВаальсаСкачать

Уравнение Ван-дер-Ваальса

Вы будете перенаправлены на Автор24

Видео:Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Что такое реальный газ

Реальным газом называют газ, между молекулами которого существуют заметные силы взаимодействия. В неидеальных, газах под высоким давлением, газах с большой плотностью взаимодействие молекул велико и его необходимо учитывать. Силы притяжения играют наиболее существенную роль на больших расстояниях между молекулами. Расстояние уменьшается, силы притяжения растут, но до определенного предела, затем они начинают уменьшаться и переходят в силы отталкивания. Притяжение и отталкивание молекул можно разделить и рассматривать и учитывать отдельно друг от друга.

Видео:Уравнение Ван-дер-Ваальса (вывод и применение). By Bogatov N.A.Скачать

Уравнение Ван-дер-Ваальса

Уравнение Ван-дер-Ваальса, описывающее состояние 1 моля реального газа, имеет вид:

где d- диаметр молекулы,

величина a вычисляется по формуле:

где $W_pleft(rright)$- потенциальная энергия притяжения двух молекул. Необходимо заметить, что газовая постоянная имеет индивидуальное значение для каждого вещества. Она отличается от молярной газовой постоянной, причем она меньше, что говорит об объединении молекул вещества в комплексы около критического состояния. Вдали от критических состояний можно использовать универсальную газовую постоянную.

С увеличением объема роль поправок в уравнении (1) становится менее существенной. И в пределе уравнение (1) переходит в уравнение состояния идеального газа для 1 моля (4):

Уравнение (4) — уравнение Менделеева — Клайперона, где m- масса газа, $R=8,31 frac$- универсальная газовая постоянная.

Это согласуется с тем фактом, что при уменьшении плотности реальные газы по своим свойствам приближаются к идеальным.

Уравнение (1) может быть записано в вириальной форме:

Для анализа изотерм уравнение (1) удобнее представить в виде:

Рассматриваемое уравнение может описывать и свойства жидкости, например плохую ее сжимаемость.

На рис.1 изображена изотерма Ван-дер-Ваальса для некоторого постоянного значения температуры T, построенная из соответствующего уравнения.

Такая зависимость на практике невозможна. Опыт показывает, что график должен иметь вид рис.2 то есть существуют области, в которых при изменении объема давление неизменно. В некоторых отрезках график изотермы параллелен оси V (рис 2). Это область фазового перехода. Жидкость и газ существую одновременно.

По мере увеличения температуры участок, отражающий состояние нахождения газа одновременно в двух фазах на графиках p(V), сужается и превращается в точку (рис. 2). Это особая точка К, в которой пропадает различие между жидкостью и паром. Это так называемая критическая точка.

Готовые работы на аналогичную тему

Итак, уравнение Ван-дер-Ваальса описывает поведение газов близких к реальным. Их можно применить к газообразной и жидкой фазам вещества. Эти уравнения отражают существование фазового перехода газ — жидкость. Показывают наличие критической точки перехода. Однако абсолютно точных количественных результатов расчеты, в которых используются вышеназванные уравнения, не дают.

Задание: Газ в количестве 1 моль находится в сосуде объемом V л при температуре $T_1$ давление газа $p_1$, а при $T_2$ давление газа $p_2$. Найти постоянные Ван-дер-Ваальса.

Запишем уравнение Ван-дер-Ваальса для одного моля реального газа для состояний 1 и 2:

Раскроем скобки в (1.1):

Вычтем $left(1.4right). из left(1.3right):$

Выразим a из (1.1):

Задание: Для реального газа, используя уравнение Ван-дер-Ваальса, получите уравнение адиабаты в параметрах V и T.

[delta Q=dU+partial A=0 left( 2.1right)]

Так как процесс адиабатный, то он идет теплообмена. Перепишем уравнение (2.1) для ван-дер-ваальсовского газа, зная, что:

Из уравнения Ван-дер-Ваальса:

Подставим (2.5) в (2.4), разделим переменные:

Ответ: Уравнение адиабаты для заданного случая имеет вид: $^<fracnu >T=const.$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 15.01.2022

Видео:Уравнение Лагранджа II рода - ч.1 - решениеСкачать

Уравнение Ван-дер-Ваальса

Уравнение Клапейрона-Менделеева хороню описывает ненасыщенный пар, далёкий до состояния насыщения, а так же газообразное состояние вещества при температурах Г, превышающих критическую Т _кр (Г > Т_кр). Для реального газа предложено более 150 уравнений, но каждое из них хорошо описывает состояние одного газа и не отражает особенностей поведения других газов. До сих пор не выведено универсальное уравнение состояния реального газа.

Для многих газов, в том числе и воздуха, наиболее простым и дающим хорошее приближение к экспериментальным данным, является уравнение, предложенное в 1873 г голландским физиком Ван-дер-Ваальсом. Он в уравнение Клапейрона—Менделеева ввёл две поправки, учитывающие собственные размеры молекул и межмолекулярное взаимодействие. Обе эти поправки обусловлены характером взаимодействия молекул в зависимости от расстояния. Между молекулами одновременно действуют силы притяжения и силы отталкивания, сложным образом зависящие от расстояния.

Молекулы реального газ Ван-дер-Ваальс рассматривал, как абсолютно твёрдые шарики диаметром d, между которыми действуют только силы притяжения. Действие сил взаимного отталкивания молекул учитывается тем, что во внимание принимаются конечные размеры молекул. Молекулы не могут сближаться на расстояние, которое меньше их диаметра d. На больших расстояниях действуют силы притяжения. Такая модель реального газа позволила учёному получить уравнение состояния, описывающее свойства газа более точно, чем уравнение Клапейрона—Менделеева.

Отклонение свойств реального газа от свойств идеального учитывают две поправки, введённые Ван-дер-Ваальсом.

1. Поправка Ь, рассматривающая собственный объём молекулы. Молекулы идеального газа представляют собой материальные точки, не имеющие собственного объёма. Выведем формулу для поправки Ь. Запишем уравнение Клапейрона-Менделеева для произвольной массы m идеального газа где R— универсальная газовая постоянная,

Р, V, Т- давление, объём, абсолютная температура идеального газа. Отсюда выразим объём V

При постоянной температуре газа Т <Т = с on s t)из (8.1) следует

где с о п s t = m ‘R’T .

Из уравнения (8.2) видно, что при постоянной температуре Т, когда давление Р неограниченно растёт ( Р —» оо), объём V —> 0. Отсюда объём V газа можно сделать сколь угодно малым, увеличивая давление Р. Но так как каждая молекула обладает собственным объёмом, то объём газа не может быть меньше суммы собственных объёмов всех его молекул даже, когда очень большое давление.

Объём плотно упакованных молекул, содержащихся в одном моле газа, обозначим через Ь. Тогда объём свободного пространства, в котором могут перемещаться молекулы, совершая хаотическое тепловое движение, равен разности (V_M — b), где V_M — молярный объём (объём одного моля газа).

Объём молекулы зависит от химической природы газа, а число молекул — от количества газа. Поэтому поправка b зависит от массы газа и его химической природы. Численное значение поправки Ь, учитывающей объём молекул, имеет постоянное значение для каждого газа и находится опытным путём.

Покажем, что поправка b в четыре раза больше собственного объёма всех Na молекул одного моля газа (N, — число Авогадро, определяющее число молекул, находящихся в одном моле газа)

где — • л ? d 3 = V — собственный объём молекулы.

Нарисуем сферу радиусом d. Внутри этой сферы могут находиться центры только двух молекул. Центры молекул не могут приближаться друг к другу ближе, чем на расстояние d, равное диаметру молекулы. Поэтому некоторая часть объёма сферы будет являться запрещённым объёмом для центров всех других молекул (рис.62). Объём V сферы радиуса d равен

На одну молекулу приходится половина объёма сферы, его называют эффективным объёмом V,,/, молекулы реального газа. Эффективный объём V_3Cp не равен собственному объёму Vo молекулы. Разделим объём сферы на 2, получим

Отсюда, поправка b (Ь = 4 ? N_A ? V₀) в четыре раза больше собственного объёма всех Na молекул одного моля газа. Поправка b определяет ту часть объёма газа, которая недоступна для движения молекул. Молекулы газа при тепловом хаотическом движении могут перемещаться в пределах объёма, равного разности (V_M — b).

Итак, константа b — поправка на собственный объём молекул учитывает отталкивание молекул на близких расстояниях. Вторая поправка учитывает силы притяжения, действующие между молекулами газа. Давление Р, которое испытывают стенки сосуда, равно давлению на газ со стороны стенок сосуда. Силами притяжения нельзя пренебрегать, когда расстояние между молекулами газа мало. Они помогают силам внешнего давления сжимать газ.

Дополнительное давление P_t, сжимающее газ и обусловленное силами молекулярного притяжения, называют молекулярным давлением. Чем ближе расположены молекулы друг к другу, тем больше силы молекулярного притяжения, а, следовательно, и молекулярное давление Р,.

Кинетическая теория газов объясняет механизм появления молекулярного давления и позволяет установить его зависимость от параметров состояния газа. Силы притяжения очень быстро убывают с увеличением расстояния между молекулами. Поэтому можно считать, что каждая молекула взаимодействует лишь с теми молекулами, которые находятся от неё на расстоянии г, равным или меньше радиуса молекулярного действия R (г N_a — число Авогадро,

V — молярный объём.

В формулу для молекулярного давления Р, подставив концентрацию п, получим

где а — коэффициент пропорциональности. Произведение а ? N_A обозначим буквой а, тогда

где а — постоянная, учитывающая особенности взаимодействия молекул. Она зависит только от химической природы газа. Величина

постоянной а определяется экспериментально.

Силы взаимодействия молекул газа с молекулами вещества стенки не рассматривали при выводе формулы для постоянной а, так как, согласно теоретическим расчётам, давление газа не зависит от вещества стенки.

Уравнение Клапейрона-Менделеева для 1 моля идеального газа имеет вид

где V _т — молярный объём.

Запишем уравнение Ван-дер-Ваальса для одного моля реального газа

где Р — внешнее давление, действующее на газ,

(Р + Pj) — сумма внешнего давления Р и молекулярного давления Р,.

В уравнение (8.4) подставим (8.3), тогда

— , стоящее в первой скобке, имеет размерность V 2

т давления. Оно учитывает притяжение молекул в результате межмолекулярного взаимодействия. Константа Ь, стоящая во второй скобке, учитывает отталкивание молекул на близких расстояниях.

Уравнение Ван-дер-Ваальса для произвольной массы т реального газа, занимающей объём V, получим, если уравнение (8.5)

умножим на число молей v (v = PL) и учтём, что V =

Уравнение Ван-дер-Ваальса описывает поведение реальных газов приближённо, но точнее, чем уравнение состояния идеального газа. Оно переходит в уравнение Клайперона-Менделеева, если объём V газа большой. Тогда можно пренебречь поправками на дополнительное молекулярное давление Р , и собственный объём молекул V о-

Уравнение Ван-дер-Ваальса количественно определяет свойства реальных газов только в области высоких температур Т и низких давлений Р. Но оно позволяет качественно описывать поведение реального газа и при высоких давлениях Р.