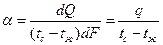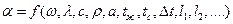В уравнении теплоотдачи ньютона рихмана удельный тепловой поток равен произведению (7 видео)

Закон Ньютона-Рихмана. Коэффициент теплоотдачи.

В практических инженерных расчетах теплоотдачу, т.е. теплообмен между поверхностью твердого тела и движущейся средой, соприкасающейся с этой поверхностью, описывают законом Ньютона-Рихмана (20).

Согласно закону Ньютона-Рихмана тепловой поток Q от жидкости к стенке или от стенки к жидкости пропорционален поверхности теплообмена F и разности температур ∆t=(t_c-t_ж) жидкости и стенки:

, [Вт] (114)

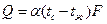
Разность температур (t_c-t_ж) или (t_ж— t_c) называют температурном напором.

Уравнение Ньютона-Рихмана для всего тепла Q_τ, передаваемого за время τ запишется:

, (115)

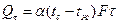
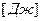
для плотности теплового потока:

, (116)

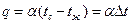
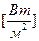
Уравнения (113)- (115) записаны для случая t_c> t_ж. Если t_ж 2 *К

Коэффициент теплоотдачи α характеризует интенсивность теплообмена на границе жидкость — стенка и численно равен количеству тепла, переданного в единицу времени через единицу поверхности, при разности температур между поверхностью и жидкостью в один градус. Коэффициент теплоотдачи α в отличие от коэффициента теплопроводности λ не является физическим параметром среды и зависит от многих факторов.

В общем случае коэффициент теплоотдачи может изменяться по поверхности теплообмена, и поэтому различают средний по поверхности и локальный или местный коэффициент теплоотдачи. Поэтому в общем случае с учетом переменности по поверхности уравнение Ньютона-Рихмана запишется:

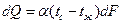
отсюда

Последнее тождество можно рассматривать как определение α: коэффициент теплоотдачи есть плотность теплового потока на границе жидкость — стенка, отнесенная к разности температур стенки и жидкости. В соответствии с сказанным в уравнениях (113)-(115) под α следует понимать его среднее значение.

Применение формулы Ньютона-Рихмана никаких принципиальных упрощений для расчета конвективной теплоотдачи не дает. Вся сложность расчета в этом случае переносится на определение коэффициента теплоотдачи, т.е. простота формулы (113)-(115) является лишь кажущейся. В общем случае является функцией многих величин:

Т.е. в общем случае α является функцией скорости движения жидкости, режима движения, физических параметров жидкости, температуры жидкости и тела, формы и размеров омываемого тела и т.д.

Инженерное решение задач конвективного теплообмена сводится чаще всего к определению α и вычислению количества переданной теплоты по формулам (2.127)-(2.129). Так как определить коэффициент теплоотдачи путем аналитического решения, приведенной в предыдущем параграфе, системы дифференциальных уравнений достаточно сложно, а в некоторых случаях и вообще невозможно, то для расчета α применяют теорию подобия.

Дата добавления: 2016-01-18 ; просмотров: 1182 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Теплофизика Л11. Уравнение теплопроводностиСкачать

Конвективный теплообмен (теплоотдача). Основной закон конвективного теплообмена

Конвективный теплообмен. Массообмен.

Факторы, влияющие на процесс теплоотдачи. Уравнение Ньютона-Рихмана. Основы теории подобия конвективного теплообмена. Теплоотдача при свободной и вынужденной конвекции.

Аналогия между процессами теплоотдачи и массообмена, основные положения, законы и уравнения массообмена.

Конвективный теплообмен (теплоотдача)

Основной закон конвективного теплообмена

Обычно жидкие и газообразные теплоносители нагреваются или охлаждаются при соприкосновении с поверхностями твердых тел. Например, дымовые газы в печах отдают теплоту нагреваемым заготовкам, а в паровых котлах – трубам, внутри которых греется или кипит вода; воздух в комнате греется от горячих приборов отопления и т. д. Процесс теплообмена между поверхностью твердого тела и жидкостью называется теплопередачей, а поверхность тела, через которую переносится теплота, — поверхностью теплообмена или теплоотдающей поверхностью.

Согласно закону Ньютона и Рихмана тепловой поток в процессе теплоотдачи пропорционален площади поверхности теплообмена F и разности температур поверхности tc и жидкости tж:

В процессе теплоотдачи независимо от направления теплового потока Q (от стенки к жидкости или наоборот) значение его можно считать положительным, поэтому разность tc-tж берут по абсолютной величине.

Коэффициент пропорциональности a называется коэффициентом теплоотдачи; его единица измерения Вт/(м2×К). Он характеризует интенсивность процесса теплоотдачи. Численное значение его равно тепловому потоку от единичной поверхности теплообмена при разности температур поверхности и жидкости в 1 К.

Коэффициент теплоотдачи обычно определяют экспериментально, измеряя тепловой поток Q и разность температур Dt= tc-tж в процессе теплоотдачи от поверхности известной площади F. Затем по формуле Q=aF½tc-tж½ рассчитывают a. При проектировании аппаратов (проведении тепловых расчетов) по этой формуле определяют одно из значений Q, F или Dt. При этом a находят по результатам обобщения ранее проведенных экспериментов.

Коэффициент теплоотдачи a зависит от физических свойств жидкости и характера ее движения. Различают естественное и вынужденное движение (конвекцию) жидкости. Вынужденное движение создается внешним источником (насосом, вентилятором, ветром). Естественная конвекция возникает за счет теплового расширения жидкости, нагретой около теплоотдающей поверхности в самом процессе теплообмена. Она будет тем сильнее, чем больше разность температур Dt= tc-tж и температурный коэффициент объемного расширения:

где n=1/r — удельный объем жидкости.

Для газов, которые в большинстве случаев приближенно можно считать идеальными, коэффициент объемного расширения можно получить, воспользовавшись уравнением Клапейрона:

температурный коэффициент объемного расширения капельных жидкостей значительно меньше, чем газов. В небольшом диапазоне изменения температур, а значит, и удельных объемов производную в уравнении можно заменить отношением конечных разностей параметров холодной (с индексом «ж») и прогретой (без индексов) жидкости:

разность плотностей rж-r=brж(t-tж) приводит к тому, что на любой единичной объем прогретой жидкости будет действовать подъемная сила Fп, равная алгебраической сумме выталкивающей архимедовой силы А=-rж×g и силы тяжести G=r×g:

Рассмотрим процесс теплоотдачи от потока теплоносителя к продольно омываемой им пластине. Скорость и температура набегающего потока постоянна и равны wж и tж.

Как уже отмечалось, частицы жидкости, непосредственно соприкасающиеся с поверхностью, адсорбируются («прилипают»). Соприкасаясь с неподвижным слоем, тормозятся и более удаленные от поверхности слои жидкости. Зона потока, в которой наблюдается уменьшение скорости (w 104 устанавливается развитый турбулентный режим (здесь d – внутренний диаметр трубы).

Состоит из величин характеризующих теплофизические свойства вещества и по существу само является теплофизической константой вещества. Значение число Pr приводится в справочниках.

В случае естественной конвекции скорость жидкости в дали от поверхности wж=0 и соответственно Re=0, но на теплоотдачу будет влиять подъемная сила Fп. Это приведет к появлению другого безразмерного параметра – числа Грасгофа:

Оно характеризует отношение подъемной силы, возникающей вследствие теплового расширения жидкости, к силам вязкости.

Большинство веществ, используемых в технике, представляет собой многокомпонентные системы. Нефтепродукты и нефть – это смесь различных углеводородов. Поэтому многие процессы теплообмена сопровождаются переносом массы.

Если в некоторой изолированной системе содержится смесь компонентов с первоначально неоднородным распределением концентраций, то в ней возникает перенос массы компонентов смеси, стремящейся к установлению равновесного (равномерного) поля концентраций.

Перенос вещества в смеси, обусловленный тепловым хаотическим движением микрочастиц вещества (молекул, ионов, атомов), называется молекулярной диффузией. Молекулярная диффузия вследствие неоднородного распределения концентраций в смеси называется концентрационной диффузией.

При перемещении, т. е. конвекции, масса компонента переносится макроскопическим элементами смеси. Перенос массы за счет совместного действия молекулярной диффузии и конвективного переноса вещества называется конвективным массообменом. Конвективный массообмен между жидкой (твердой) поверхностью и окружающей средой называется массоотдачей. Плотность потока массы при концентрационной диффузии определяют уравнением, аналогичным уравнению Ньютона-Рихмана:

где bМ — коэффициент массоотдачи, отнесенный к разности концентраций диффундирующего вещества, м/с;

mic и mio – концентрации вещества на поверхности массоотдачи и в окружающей среде.

Поток массы от поверхности площадью F определяют по формуле:

Числа подобия конвективного массообмена

Диффузионное число подобия Нуссельта В научной литературе его часто обозначают как число Шервуда которое показывает отношение действительной плотности потока при массоотдаче к плотности потока массы при чистой диффузии.

При конвективном массообмене вместо теплового числа подобия Прандтля Pr используют диффузионное число Прандтля в научной литературе его часто обозначают как число подобия Шмидта Этот критерий подобия при определенных условиях является мерой подобия скоростных и концентрационных полей в потоке.

При наличии фазового перехода используют число подобия

. где r – теплота фазового перехода;

Dt – разность температур фазового перехода и действительной температуры в процессе. Число К является мерой отношения теплового потока, идущего на фазовое превращение вещества, к теплоте перегрева (переохлаждения) одной из фаз. Кроме того, используются известные критерии подобия Re и Gr.

В общем случае при стационарном процессе конвективный массообмен описывается уравнением подобия:

Неизвестные коэффициенты С, iw, g, d, iPi определяются на основе эксперимента.

Частные случаи конвективного теплообмена

Поперечное обтекание одиночной трубы и пучка труб

Экспериментальные данные по теплоотдаче при поперечном обтекании одиночной круглой трубы спокойным, нетурбулизированным потоком обобщается формулой:

значение коэффициента С и показателя степени n в зависимости от критерия Reж приведены ниже:

Видео:Теплофизика Л4. Элементарное описание теплообмена. Закон Ньютона-РихманаСкачать

10.2. Закон Ньютона-Рихмана

Процесс теплообмена между поверхностью тела и средой описывается законом Ньютона-Рихмана, которая гласит, что количество теплоты, передаваемая конвективным теплообменом прямо пропорционально разности температур поверхности тела (t_‘ст)и окружающей среды (t_‘ж):Q = α · (t_‘ст — t_‘ж)·F , (10.1)илиq = α · (t_‘ст — t_‘ж) , (10.2)где: коэффициент теплоотдачи [Вт/(м 2 К)], характеризует интенсивность теплообмена между поверхностью тела и окружающей средой.

Факторы, которые влияют на процесс конвективного теплообмена, включают в этот коэффициент теплоотдачи. Тогда коэффициент теплоотдачи является функцией этих параметров и можно записать эту зависимость в виде следующего уравнения:α = f₁(Х; Ф; l_o; x_c; y_c; z_c; w_o; θ; λ; а; с_р; ρ; ν; β) , (10.3)где: Х – характер движения среды (свободная, вынужденная);

Ф – форма поверхности;

l_o – характерный размер поверхности (длина, высота, диаметр и т.д.);

θ = (t_‘ст — t_‘ж) – температурный напор;

λ – коэффициент теплопроводности среды;

а – коэффициент температуропроводности среды;

с_р –изобарная удельная теплоемкость среды;

ρ –плотность среды;

ν – коэффициент кинематической вязкости среды;

β – температурный коэффициент объемного расширения среды.

Уравнение (10.3) показывает, что коэффициент теплоотдачи величина сложная и для её определения невозможно дать общую формулу. Поэтому для определения коэффициента теплоотдачи применяют экспериментальный метод исследования.

Достоинством экспериментального метода является: достоверность получаемых результатов; основное внимание можно сосредоточить на изучении величин, представляющих наибольший практический интерес.

Основным недостатком этого метода является, что результаты данного эксперимента не могут быть использованы, применительно к другому явлению, которое в деталях отличается от изученного. Поэтому выводы, сделанные на основании анализа результатов данного экспериментального исследования, не допускают распространения их на другие явления. Следовательно, при экспериментальном методе исследования каждый конкретный случай должен служить самостоятельным объектом изучения.