В уравнении гармонических колебаний x acos t 0 величина x обозначает

Видео:Физика. 11 класс. Уравнение и графика гармонических колебаний /03.09.2020/Скачать

В уравнении гармонических колебаний х = A cos(wt + ф0) величина w называется 1) фазой 2) частотой

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Ваш ответ

Видео:Урок 327. Гармонические колебанияСкачать

решение вопроса

Видео:Колебательное движение. Уравнение гармонических колебаний | ФизикаСкачать

Похожие вопросы

• Все категории
• экономические 43,429
• гуманитарные 33,634
• юридические 17,906
• школьный раздел 608,227
• разное 16,858

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Гармонические колебания

Техника и окружающий мир являются примерами того, что существуют такие процессы, которые повторяются через определенные промежутки времени, то есть периодически. Их называют колебательными.

Видео:5.4 Уравнение гармонических колебанийСкачать

Колебательные движения. Формулы

Такие движения относят к явлениям с разной физической природой с подчинением общим закономерностям. Запись колебания тока в электрической цепи и математического маятника производится одним и тем же уравнением. Различная природа колебательных движений позволяет рассматривать их с единой точки зрения, исходя из общности закономерностей.

Механические колебания – это периодические или непериодические изменения физической величины, описывающей механическое движение (скорость, перемещение и так далее).

Когда в заданной среде атомы располагаются очень близко или молекулы испытывают силовое воздействие, наблюдается возбуждение механических колебаний. Это говорит о том, что процесс будет иметь конечную скорость, зависящую от свойств среды, которая распространяется от точки к точке. Так возникают механические волны. Явный пример – звуковые волны в воздухе.

Волновые процессы и колебания разной природы имеют много общего, а их распространение может быть описано аналогичными математическими уравнениями. Это подтверждает единство материального мира.

Видео:Урок 335. Анализ графика гармонических колебанийСкачать

Гармонические колебания. Определение

В механике предусмотрено движение поступательно, вращательно и с наличием колебаний.

Механические колебания – это движения тел, которые повторяются точно или приблизительно за определенные одинаковые временные промежутки.

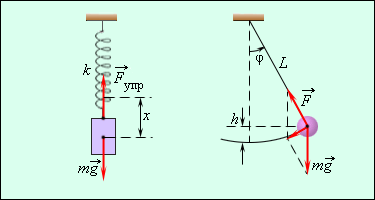
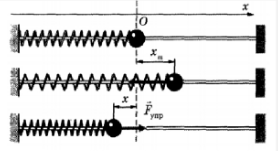
Функция x = f ( t ) объясняет закон движения тела с наличием колебаний. При графическом изображении дается представление о протекании колебательного процесса во времени. Рисунок 2 . 1 . 1 наглядно показывает принцип простых колебательных систем груза на пружине или математического маятника.

Рисунок 2 . 1 . 1 . Механические колебательные системы.

Механические колебания подразделяют на свободные и вынужденные.

Действия внутренних сил системы после выведения из равновесия порождают свободные колебания. Примером могут служить колебания груза на пружине или маятника. Если их действие происходит под воздействием внешних сил, тогда их называют вынужденными.

Простейшим видом колебаний являются гармонические колебания, которые описываются уравнением x = x m cos ( ω t + φ 0 ) , где x – смещение тела от положения равновесия, x m – амплитуда колебаний, ω – циклическая или круговая частота, t – время.

Величина, располагаемая под знаком косинуса, получила название фазы гармонического процесса: φ = ω t + φ 0 . Если t = 0 , φ = φ 0 , тогда φ 0 рассматривается в качестве начальной фазы.

Период колебаний Т – это минимальный промежуток времени, через который происходят повторения движения тела. Величина, обратная периоду колебаний, называют частотой колебаний f = 1 T .

Частота гармонических колебаний показывает их количество, совершаемое за единицу времени, измеряемая в герцах ( Г ) . Связь с циклической частотой ω и периодом T выражается с помощью формулы:

ω = 2 π f = 2 π T .

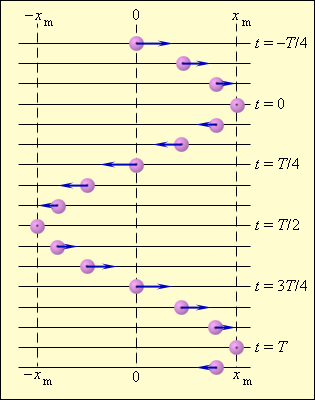
Рисунок 2 . 1 . 2 показывает гармонические колебания тел с разными положениями тел. Данный эксперимент наблюдается в специальных условиях при наличии периодических вспышек освещения, называемого стробоскопическим. Для изображения векторов скорости тела в разные моменты времени используют стрелки.

Рисунок 2 . 1 . 2 . Стробоскопическое изображение гармонических колебаний. Начальная фаза φ 0 = 0 . Интервал времени между последовательными положениями тела τ = T 12 .

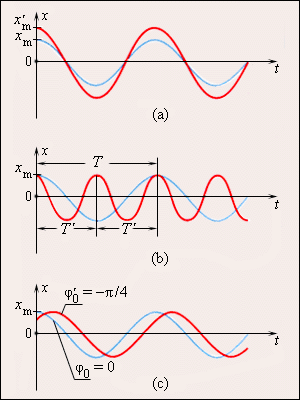
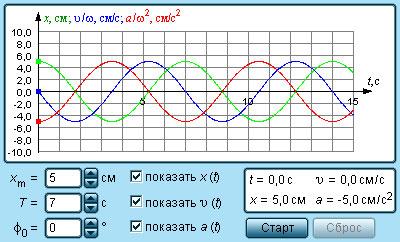
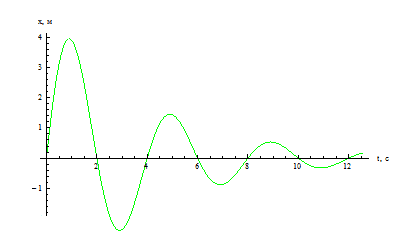
На графике 2 . 1 . 3 . показаны изменения, происходящие во время гармонического процесса, при изменении амплитуды колебаний x m , или периода Т (частоты f ), или начальной фазы φ 0 .

Рисунок 2 . 1 . 3 . Во всех трех случаях для синих кривых φ 0 = 0 : a – красная кривая отличается от синей только большей амплитудой ( x ‘ m > x m ) ; b – красная кривая отличается от синей только значением периода ( T ‘ = T 2 ) ; с – красная кривая отличается от синей только значением начальной фазы φ 0 ‘ = — π 2 р а д .

Видео:Выполнялка 53.Гармонические колебания.Скачать

Гармонический закон

Если колебания совершаются вдоль прямой О х , тогда направление вектора скорости аналогично. Определение скорости движения тела υ = υ x определяют из выражения υ = ∆ x ∆ t ; ∆ t → 0 .

Отношение ∆ x ∆ t при ∆ t → 0 математика трактует как вычисление производной функции x ( t ) за определенное время t . Обозначение принимает вид d x ( t ) d t , x ‘ ( t ) или x ˙ .

Гармонический закон движения записывается в качестве x = x m cos ( ω t + φ 0 ) . После вычисления производной формула приобретает вид:

υ = x ˙ ( t ) = — ω x m sin ( ω t + φ 0 ) = ω x m cos ω t + φ 0 + π 2 .

Слагаемое + π 2 считают изменением начальной фазы. Достижение максимального значения скорости по модулю υ = ω x m производится при прохождении тела через положение равновесия, то есть x = 0 . Аналогично определяют ускорение a = a x . Тогда a = ∆ υ ∆ t , ∆ t → 0 . Отсюда следует, что a равняется производной функции υ ( t ) за время t или второй производной функции x ( t ) . Подставив выражения, получим

a = υ ˙ ( t ) = x ¨ ( t ) = — ω 2 x m cos ( ω t + φ 0 ) = — ω 2 x ( t ) .

Наличие отрицательного знака указывает на то, что ускорение a ( t ) имеет противоположный смещению x ( t ) знак. Исходя из второго закона Ньютона, сила, которая заставляет совершать колебательные движения, направляется в сторону положения равновесия x = 0 .

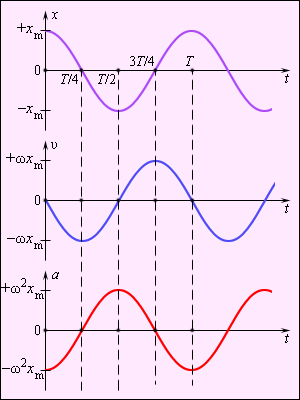
На рисунке 2 . 1 . 4 изображены графики, где имеются зависимости скорости, ускорения, совершающие гармонические колебания.

Рисунок 2 . 1 . 4 . Графики координаты x ( t ) , скорости υ ( t ) и ускорения a ( t ) тела, совершающего гармонические колебания.

Рисунок 2 . 1 . 5 . Модель гармонических колебаний.

Видео:Гармонические колебанияСкачать

В уравнении гармонического колебания х = Acos( t + 0 )

В уравнении гармонического колебания х = Acos( t + 0 ) величина, стоящая под знаком косинуса, называется
nbsp;(*ответ*) фазой
nbsp;начальной фазой
nbsp;смещением от положения равновесия
nbsp;повторяющейся частотой
Движение электронного заряда, при котором он не испускает электромагнитные волны
nbsp;(*ответ*) существует, это равномерное движение по окружности
nbsp;не существует
nbsp;существует, это равномерное прямолинейное движение
nbsp;существует, это движение с большой скоростью
Для того чтобы слушать радиостанцию quot;Открытое радиоquot;, которая вещает на частоте 102,5 МГц, радиоприемник необходимо настроить на длину волны
nbsp;(*ответ*) 2,927 м
nbsp;2,927 мм
nbsp;2,927 см
nbsp;2,927 дм
Емкостное противодействие конденсатора на частоте 50 Гц одинаково 100 Ом. На частоте 12,5 Гц емкостное противодействие одинаково _ Ом
nbsp;(*ответ*) 400
nbsp;200
nbsp;600
nbsp;800
Если в некий момент медли в точке с координатами (х, у, z) напряженность электронного поля Е =(Е, 0,0), а индукция магнитного поля В=(0,0. В), то плоская электрическая волна quot;бегаетquot; в декартовой системе координат
nbsp;(*ответ*) параллельно оси Y
nbsp;параллельно оси X
nbsp;параллельно оси Z
nbsp;такая волна невозможна
Если емкость колебательного контура увеличить в 3 раза, а индуктивность уменьшить в 3 раза, то при условии, что активным противодействием пренебречь, частота собственных колебаний контура
nbsp;(*ответ*) не изменится
nbsp;будет уменьшатся
nbsp;будет возрастать
nbsp;станет одинаковой нулю
Если индуктивность колебательного контура увеличить в 20 раз, а емкость уменьшить в 5 раз, период собственных колебаний контура_ раза
nbsp;(*ответ*) возрастет в 2
nbsp;уменьшится в 2
nbsp;возрастет в 4
nbsp;уменьшится в 4
Если источник звука, колеблющийся с периодом 0,003 с, возбуждает в воде волны длиной 3 м, то скорость звука в воде одинакова _ м/с
nbsp;(*ответ*) 1000
nbsp;900
nbsp;100
nbsp;90
Если при увеличении силы тока в катушке индуктивности энергия магнитного поля катушки увеличилась в 4 раза, то магнитный поток через катушку
nbsp;(*ответ*) возрос в 2 раза
nbsp;возрос в 4 раза
nbsp;уменьшился в 4 раза
nbsp;остался минувшим
Заряженный конденсатор замыкают на катушку, активное сопротивление проводов которой ничтожно малюсенько. Заряд на положительно заряженной пластинке конденсатора будет
nbsp;(*ответ*) колебаться от начального значения до обратного, временами меняя символ
nbsp;подрастать до некого наибольшего значения
nbsp;спадать до нуля
nbsp;колебаться от исходного значения до нуля и обратно
К вертикально весящей нерастянутой пружине жесткостью к прикрепляют груз массой m и резко отпускают. Начинаются колебания. Какова амплитуда этих колебаний
nbsp;(*ответ*) mg / k
nbsp;mg / 2k
nbsp;3mg / 2k
nbsp;2mg / k
Колебательный контур радиоприемника исполняет функцию
nbsp;(*ответ*) приема всех электрических волн
nbsp;выделения из электрической волны модулирующего сигнала
nbsp;усиления сигнала одной избранной волны
nbsp;выделения электрических волн, совпадающих по частоте с собственными колебаниями

Видео:Как решить уравнение колебаний? | Олимпиадная физика, механические гармонические колебания, 11 классСкачать

Гармонические колебания

теория по физике 🧲 колебания и волны

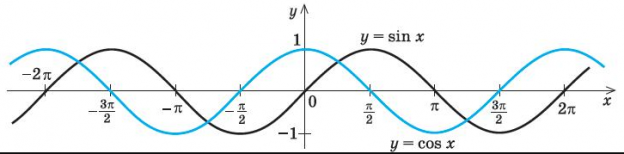
Гармоническими законами называют законы синуса и косинуса. Следовательно, гармоническими колебаниями называют те колебания, при которых координата тела изменяется синусоидально или косинусоидально.

Гармонические колебания — колебания, при которых координата тела изменяется с течением времени по гармоническому закону.

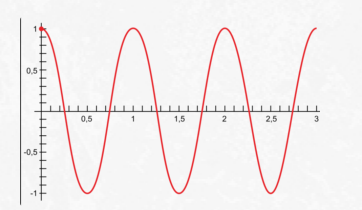
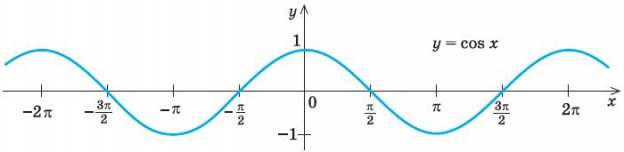
Ниже представлен график косинусоидальной функции. Обратите внимание, что косинус при возрастании аргумента от нуля сначала меняется медленно, а потом он все быстрее и быстрее приближается к нулю. Пройдя через него, его модуль снова быстро возрастает. Но по мере приближения к максимальному значению он снова замедляется. Точно так же меняются координаты свободно колеблющегося тела.

Важно! Гармоническими можно считать только те колебания, что совершаются грузом, закрепленном на пружине, или математическим маятником, отклоняемым на малый угол, при котором ускорение тела пропорционально его смещению.

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Уравнение движения гармонических колебаний

Известно, что ускорение колеблющегося на пружине груза пропорционально его смещению от положения равновесия:

Также известно, что ускорение есть вторая производная координаты. Следовательно, при свободных колебаниях координата изменяется со временем так, что вторая производная координаты по времени прямо пропорциональна самой координате и противоположна ей по знаку.

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

x″ = − x m a x cos . t = − x

Видно, что в этом случае теряется величина k m . . , служащая постоянной для каждой колебательной системы. Чтобы получить ее во второй производной, нужно усложнить функцию до следующего вида:

x = x m a x cos . √ k m . . t

Тогда первая производная примет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

x′ = − √ k m . . x m a x sin . √ k m . . t

Вторая производная примет вид:

x″ = − k m . . x m a x cos . √ k m . . t = − k m . . x

Так как мы получили ровно такое же выражение, то описать свободные колебания можно уравнениями следующего вида:

x = x m a x sin . √ k m . . t

x = x m a x cos . √ k m . . t

Обозначим постоянную величину √ k m . . , зависящую от свойств системы, за ω₀:

x = x m a x sin . ω 0 t

x = x m a x cos . ω 0 t

Само уравнение движения, описывающего свободные колебания, примет вид:

Видео:Урок 330. Скорость и ускорение при гармонических колебанияхСкачать

Период и частота гармонических колебаний

Минимальный промежуток времени T, через который движение тела полностью повторяется, называют периодом колебания. Зная его, можно вычислить частоту колебаний, равную числу колебаний в единицу времени. Эти величины связаны между собой выражением:

Через промежуток времени, равный периоду T и соответствующий изменению аргумента косинуса на ω 0 T , движение тела повторяется, и косинус принимает прежнее значение. Но из математики известно, что наименьший период косинуса равен 2π. Следовательно:

ω 0 = 2 π T . . = 2 π ν

Таким образом, величина ω 0 представляет собой число колебаний тела, но не за 1 секунду, а за 2 π секунд. Эта величина называется циклической (круговой) частотой. А частоту свободных колебаний называют собственной частотой колебательной системы.

Видео:Тема 1. Колебательное движение. Гармонические колебания. Уравнение гармонических колебанийСкачать

Зависимость частоты и периода свободных колебаний от свойств системы

Изначально за величину ω 0 мы принимали постоянную, характеризующую свойства системы:

Теперь мы выяснили, что циклическая частота связана с периодом и частотой колебаний. Следовательно, период и частота колебаний также зависят от свойств системы:

ω 0 = √ k m . . = 2 π T . . = 2 π ν

Отсюда период и частота колебаний соответственно равны:

T = 2 π ω 0 . . = 2 π √ m k . .

ν = 1 2 π . . √ k m . .

Вспомним, что свойства колебательной системы математического маятника определяются постоянной величиной g l . . . Следовательно, циклическая частота для него равна:

Отсюда период и частота колебаний математического маятника соответственно равны:

T = 2 π ω 0 . . = 2 π √ l g . .

ν = 1 2 π . . √ g l . .

Эта формула была впервые получена и проверена на опыте голландским ученым Г. Гюйгенсом, современником И. Ньютона.

Период колебания возрастает с увеличением длины маятника. От массы маятника он не зависит. Это легко проверить на опыте с различными маятниками. Зависимость периода от ускорения свободного падения также легко прослеживается. Чем меньше величина g, тем больше период колебания маятника, и, следовательно, тем медленнее идут часы с маятником. Так, часы с маятником в виде груза на стержне отстанут в сутки почти на 3 с, если их поднять из подвала на верхний этаж Московского университета, который находится на высоте 200 м. И это только за счет уменьшения ускорения свободного падения с высотой.

Зависимость периода колебаний маятника от значения g используется на практике. Измеряя период колебания, можно легко измерить g. Ускорение свободного падения меняется с географической широтой. Но и на данной широте оно неодинаково, так как плотность земной коры неоднородна. В районах, где залегают более плотные породы, ускорение свободного падения принимает большие значения.

Пример №1. Сколько колебаний совершает математический маятник длиной 4,9 м за время 5 минут?

Искомое число колебаний равно отношению времени к периоду колебаний:

Период колебаний для математического маятника определяется формулой:

N = t 2 π . . √ g l . . = 300 2 · 3 , 14 . . √ 9 , 8 4 , 9 . . ≈ 68

Видео:Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

Фаза колебаний

При заданной амплитуде гармонических колебаний координата колеблющегося тела в любой момент времени однозначно определяется аргументом косинуса или синуса, который равен ω 0 t . Обозначим его за ϕ и получим:

Величину ϕ, стоящую под знаком косинуса или синуса, называют фазой колебаний, описываемой этой функцией. Выражается фаза в угловых единицах — радианах (рад).

Фаза определяет значение не только координаты, но и других физических величин (к примеру, скорости и ускорения, которые также изменяются по гармоническому закону). Отсюда можно сделать вывод, что фаза определяет при заданной амплитуде состояния колебательной системы в любой момент времени.

Колебания с одинаковыми частотами и амплитудами могут отличаться друг от друга фазами. Так как ω 0 = 2 π T . . , фаза определяется формулой:

ϕ = ω 0 t = 2 π t T . .

t T . . — отношение, которое указывает, какая часть периода прошла от момента начала колебаний. Любому моменту времени, выраженному в долях периода, соответствует значение фазы, выраженное в радианах. К примеру:

Можно изобразить на графике зависимость координаты колеблющейся точки не от времени, а от фазы. В этом случае графиком также будет являться косинусоида (или синусоида), но аргументом функции будет не время (период), а фаза, выражающаяся в радианах (см. рис.).

Синус от косинуса отличается только смещением аргумента на π 2 . . (см. рис. ниже). Поэтому для описания гармонических колебаний можно использовать как синусоидальный, так и косинусоидальный закон.

Выбор закона зависит от условий задачи. Если колебания начинаются с того, что тело выводят из положения равновесия и отпускают, удобнее пользоваться косинусоидальным законом, поскольку в начальный момент времени косинусоида показывает, что это тело отклонено максимально, а не находится в положении равновесия. Если для того чтобы начались колебания, совершают толчок, удобнее использовать синусоидальный закон, так как начальному моменту времени на синусоиде соответствует положение равновесия.

Колебания, совершаемые по закону синуса и косинуса, отличаются только фазой, которая смещена на значение, равное π 2 . . . Это значение называют сдвигом фаз, или их разностью. Поэтому косинусоидальная функция также может быть записана как:

x = x m a x cos . ω 0 t = x m a x sin . ( ω 0 t + π 2 . . )

Видео:Якута А. А. - Механика - Гармонические колебания. Собственные затухающие колебанияСкачать

Превращение энергии при гармонических колебаниях

Чтобы описать превращения энергии при гармонических колебаниях, условимся, что силой трения будем пренебрегать. Для описания обратимся к рисунку ниже.

Точке О на рисунке соответствует положение равновесия шарика. Если его оттянуть на расстояние x_max, равное амплитуде, пружина получит потенциальную энергию, которая примет в этом положении максимальное значение, равное:

W p m a x = k x 2 m a x 2 . .

Когда шарик отпускают, возникает сила упругости, под действием которой шарик устремляется влево. По мере уменьшения расстояния между точкой максимального отклонения и положением равновесия уменьшается и потенциальная энергия. Но в это время увеличивается кинетическая энергия шарика. Когда шарик проходит через положение равновесия в первый раз, его потенциальная энергия становится равной нулю, а кинетическая энергия обретает максимальное значение (скорость в этот момент времени тоже максимальна):

W k m a x = m v 2 m a x 2 . .

После прохождения точки О расстояние между шариком и положением равновесия снова увеличивается, и потенциальная энергия растет. Кинетическая же энергия при этом уменьшается. А в крайнем положении слева она становится равной нулю, в то время как потенциальная энергия снова примет максимальное значение.

Так как мы условились пренебрегать трением, данную колебательную систему можно считать изолированной. Тогда в ней должен соблюдаться закон сохранения энергии. Согласно ему, полная механическая энергия системы равна:

W = W p + W k = k x 2 x 2 . . + m v 2 x 2 . . = k x 2 m a x 2 . . = m v 2 m a x 2 . .

В действительности свободные колебания всегда затухают, так как в колебательной системе действует сила трения. И часть механической энергии рассеивается в виде тепла. Пример графика затухающих колебаний выглядит следующим образом:

Пример №2. Груз, прикрепленный к пружине, колеблется на горизонтальном гладком стержне. Найдите отношение кинетической энергии груза к его потенциальной энергии системы в момент, когда груз находится в точке, расположенной посередине между крайним положением и положением равновесия.

Так как груз находится посередине между крайним положением и положением равновесия, его координата равна половине амплитуды:

В это время потенциальная энергия груза будет равна:

W p = k x 2 2 . . = k ( x m a x 2 . . ) 2 2 . . = k x 2 m a x 8 . .

Согласно закону сохранения энергии, кинетическая энергия в это время равна:

Полная механическая энергия системы равна максимальной потенциальной энергии:

W = W p m a x = k x 2 m a x 2 . .

Тогда кинетическая энергия равна:

W k = k x 2 m a x 2 . . − k x 2 m a x 8 . .

Следовательно, отношение кинетической энергии к потенциальной будет выглядеть так:

W k W p . . = k x 2 m a x 2 . . − k x 2 m a x 8 . . k x 2 m a x 8 . . . . = k x 2 m a x 2 . . 8 k x 2 m a x . . − 1 = 4 − 1 = 3

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Резонанс

Самый простой способ возбуждения незатухающих колебаний состоит в том, что на систему воздействуют внешней периодической силой. Такие колебания называют вынужденными.

Работы силы над такой системой обеспечивает приток энергии к системе извне. Приток энергии не дает колебаниям затухнуть, несмотря на действие сил трения.

Особый интерес вызывают вынужденные колебаний в системе, способной совершать свободные колебания. Примером такой системы служат качели. Их не получится отклонить на большой угол всего лишь одним толчком. Если их толкать то в одну, то в другую сторону, тоже ничего не получится. Но если подталкивать качели всякий раз, как они сравниваются с нами, можно раскачать их очень сильно. При этом не нужно прикладывать большую силу, но на это понадобится время. Причем после каждого такого толчка амплитуда колебаний качелей будет увеличиваться до тех пор, пока не достигнет своего максимального значения. Такое явление называется резонансом.

Резонанс — резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему, с частотой свободных колебаний.

Графически явление резонанса можно изобразить как резкий скачок графика вверх (см. рис. выше). Причем высота «зубца», или амплитуда колебаний, будет зависеть от величины сил трения. Чем больше сила трения, тем меньше при резонансе возрастает амплитуда вынужденных колебаний. Это можно продемонстрировать графиками на рисунке ниже. Графику 1 соответствует минимальное трение, графику 3 — максимальное.

На явлении резонанса основан принцип работы частотомера — устройства, предназначенного для измерения частоты переменного тока. Он состоит из набора упругих пластин, которые закреплены на одной планке. Каждая пластина обладает определенной собственной частотой колебаний, которая зависит от упругих свойств, длины и массы. Собственные колебания пластин известны. Под действием электромагнита планка, а вместе с ней и пластины совершают вынужденные колебания. Но лишь та пластина, собственная частота которой совпадает с частотой колебаний планки, будет иметь большую амплитуду колебаний. Таким образом, определяется частота переменного тока.

Пример №3. Автомобиль движется по неровной дороге, на которой расстояние между буграми равно приблизительно 8 м. Период свободных колебаний автомобиля на рессорах 1,5 с. При какой скорости автомобиля его колебания в вертикальной плоскости станут особенно заметными?

Колебания автомобиля в вертикальной плоскости будут заметны тогда, когда частота наезда на бугры сравняется с частотой свободных колебаний автомобиля на рессорах. Поскольку частота обратно пропорциональна периоду, можно сказать, что резонанс будет достигнут тогда, когда автомобиль будет наезжать на бугры каждые 1,5 секунды. Зная расстояние между буграми и время, можем вычислить скорость:

v = s t . . = 8 1 , 5 . . ≈ 5 , 33 ( м с . . ) ≈ 19 , 2 ( к м ч . . )

Смещение груза пружинного маятника меняется с течением времени по закону x = A cos . 2 π T . . t , где период Т = 1 с. Через какое минимальное время, начиная с момента t = 0, потенциальная энергия маятника вернется к своему исходному значению?

🔥 Видео

10 класс, 19 урок, График гармонического колебанияСкачать

"Гармонические колебания, часть 2 (дифференциальное исчисление)"Скачать

График гармонического колебания | Алгебра 10 класс #23 | ИнфоурокСкачать

Механические колебания и все что нужно про них знать. Онлайн школа EXAMhackСкачать