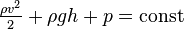Видео:Закон БернуллиСкачать

Уравнение Бернулли Статическое и динамическое давление

Вследствие наличия сил притяжения взаимное смещение частиц жидкости сопровождается некоторым сопротивлением, которое подобно механическому трению между мелкими частицами твердого вещества и называется внутренним трением, или вязкостью, жидкости. Вязкость жидкости проявляется, например, сопротивлением при помешивании жидкости, замедлением при падении в жидкости предметов и т. д.
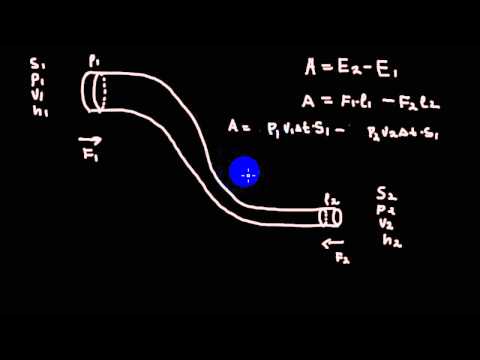
Рассмотрим вначале стационарное течение идеальной жидкости (идеальной называется несжимаемая жидкость, не имеющая вязкости; стационарным называется течение, при котором величина скорости в любой точке жидкости со временем не изменяется). Установим для этих условий соотношение между давлением р в жидкости, скоростью движения v ее частиц и положением их в поле силы тяжести, характеризуемое высотой Л над некоторым уровнем отсчета (рис. 2).
Уравнение Бернулли
В соответствии с законом сохранения энергии полная энергия некоторой массы m (имеющей объем V) идеальной жидкости при течении остается неизменной, так как в ней отсутствуют потери на внутреннее трение.
Полная энергия составляется из потенциальной энергии давления (Еn = pV), потенциальной энергии тяжести (E«п = mgh) и кинетической энергии (Ек = m υ 2 /2). На основании сказанного: pV + mgh + (m υ 2 /2) = const.
Соответственно для каких-либо двух положений массы т идеальной жидкости, например в точках А и Б (рис. 2):
Если предпоследнее уравнение разделить почленно на объем V жидкости, то учитывая, что m/V есть плотность ρ жидкости, получим:
Это и есть уравнение Бернулли.
Для движения жидкости в горизонтальных трубках силу тяжести можно не учитывать и тогда уравнение Бернулли принимает вид:
Из этого уравнения следует вывод, называемый правилом Бернулли: давление невязкой жидкости, текущей по горизонтальной трубе, выше там, где скорость ее меньше, и наоборот.
Пример расчета по формуле
Рассмотрим течение жидкости по трубе с неодинаковым сечением. Течение называется непрерывным, если через любое сечение трубы в единицу времени протекает одинаковое количество (объем) жидкости. При этом скорость движения жидкости на участках трубы обратно пропорциональна площади их сечений.
Действительно не трудно доказать, что объем V0 жидкости, протекающей в единицу времени через любое сечение трубы, может быть выражен произведением площади S сечения трубы на скорость υ течения жидкости: V0=Sυ. По условию этот объем постоянен для любого сечения трубы, следовательно,
т. е. произведение скорости течения жидкости на поперечное сечение струи есть величина постоянная. Это соотношение называют уравнением неразрывности струи.
Если обозначить сечение и скорость движения на участках трубы соответственно S1 и υ1 S2 и υ2, то согласно сказанному:
Скорость течения жидкости в трубе с переменным сечением обратно пропорциональна площади этих сечений.
При этом в соответствии с правилом Бернулли на участках меньшего сечения трубы давление будет ниже, на участках большего сечения — выше (рис. , а). Поясним механизм этого явления. При переходе на участок трубы меньшего сечения (линия ab на рис. , б) частицы жидкости ускоряются, на что затрачивается часть силы Р4, создающей давление на более широком участке (по условию равновесия частиц жидкости Р1= Р2+Fу, где Р2 — сила, создающая давление на суженном участке, Fу — сила, обеспечивающая ускорение частиц).
Наоборот, при переходе на участок с большим сечением (линия cd на рис. 82, б) частицы жидкости набегают на лежащую впереди и более медленно двигающуюся массу жидкости и, затормаживаясь, создают дополнительную силу Fт, повышающую давление на более широком участке (аналогично P3=P2 + Fт).
Можно подобрать условия, при которых давление жидкости в сужен ном участке трубы станет ниже атмосферного и тогда в этом месте струя будет обладать всасывающим действием. Всасывающее действие струи газа, пара или воды, выходящей из суженного отверстия с большой скоростью, используется в ряде приборов, применяемых в медицинской практике (ингалятор, водоструйный насос и др.).
Паровой ингалятор
Это прибор для вдыхания жидких лекарственных веществ в распыленном виде. Он состоит из кипятильника В, стакана К с лекарственной жидкостью и вставленной в него тонкой трубкой Т и направляющего патрубка С. Струя пара выходит из трубки кипятильника с большой скоростью. Вследствие этого давление около ее отверстия падает и лекарственная жидкость, всасываясь по трубке Т, поступает в струю, распыляется и, смешиваясь с паром, вдыхается больным через патрубок С
Водоструйный насос состоит из стеклянного сосуда Н, в который впаяно три трубки. Трубка имеет на конце коническое сужение. Насос присоединяется к водоводу и колбе К, из которой производится отсасывание. Вода, имеющая достаточно высокое давление, выходит из суженного конца трубки 1 с большей скоростью. Давление у отверстия трубки резко снижается и в сосуд А через трубку 2 засасывается воздух или жидкость, которые вместе с водой удаляются через трубку 3. Водоструйный насос удобен тем, что он не имеет вращающихся частей, требующих смазки, бесшумен и гигиеничен. Поэтому он часто применяется в лабораториях, операционных и т. п.
В уравнении Бернулли давление р называется статическим давлением рс жидкости. Оно может быть измерено обычным манометром, который двигается вместе с жидкостью, или практически при помощи неподвижной манометрической трубки, плоскость отверстия которой расположена параллельно направлению движения жидкости.
Второй член уравнения Бернулли (ρυ2/2)также имеет размерность давления и называется динамическим давлением рд в жидкости. Сумма статического и динамического давлений называется полным давлением р в жидкости:
Для измерения его применяют манометрическую трубку, изогнутую под прямым углом и помещенную отверстием навстречу движению жидкости. Частицы жидкости, заходящие в отверстие трубки полностью тормозятся в ней: скорость υ2 частиц жидкости в отверстии рав няется нулю: υ 2=0. Тогда по уравнению Бернулли
Следовательно, давление р2 в трубке:
где р1 — давление и υ1 — скорость движущейся жидкости
Если в струю жидкости поставить рядом две такие трубки, то разность уровней в трубках будет соответствовать динамическому давлению. На этом основан способ измерения скорости движения жидкости или газа В струю погружают две скрепленные вместе измерительные трубки, прямую и изогнутую (подобное устройство называется трубкой Пито), которые соединяются с U= образным манометром. Манометр покажет динамическое давление, по величине которого, пользуясь приведенной выше формулой, вычисляют искомую скорость:
Статья на тему Уравнение Бернулли
Похожие страницы:
Понравилась статья поделись ей
Leave a Comment
Для отправки комментария вам необходимо авторизоваться.
Видео:Урок 134. Применения уравнения Бернулли (ч.1)Скачать

Гидродинамика. Уравнение Бернулли для идеальной жидкости.
Уравнение Даниила Бернулли, доказанное в 1738 г, считают основным уравнением гидродинамики. Данное выражение демонстрирует закон сохранения энергии движущейся жидкости.
Закономерность (уравнение) Бернулли для стационарного потока идеальной несжимаемой жидкости выглядит так:
h —высота, на которой размещен анализируемый элемент жидкости;
p — давление на участке, где размещен центр массы анализируемого элемента жидкости,
Константу в правой части принято называть полным давлением и обусловлена она линией тока.
Первое слагаемое – ρv 2 /2 представляет собой динамическое давление. Оно устанавливается течением жидкости.
Последующее слагаемое — (ρ g h) описывает гидростатическое (весовое) давление. Это давление, сформированное весом вертикального столба жидкости некоторой высоты h.
Эти две величины иллюстрируют кинетическую и потенциальную энергии, приходящейся на единицу объёма жидкости.
Третья величина – p – статическое давление. Это давление друг на друга соседних слоев жидкости. Его получится фиксировать с помощью манометра с текущей жидкостью
Полное давление включает в себя весовое (ρ g h), статическое (p) и динамическое (pv 2 /2 ) давление.
Закон (уравнение) Бернулли – в установившемся движении идеальной жидкости полное давление будет величиной неизменной для всякого поперечного сечения трубки тока.
Основываясь на уравнении Бернулли получаем, что при сужении сечения потока, по причине роста скорости, понижается динамическое и статическое давление. Перефразировав получаем — чем выше скорость потока идеальной жидкости, тем ниже ее давление.
Факт понижения давления при росте скорости потока заложен в основу эксплуатации разнообразных типов расходомеров, водо- и пароструйных насосов. Практическое использование закономерностей Бернулли повлияло на формирование технической гидромеханической науки — гидравлики.
Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

В уравнении бернулли слагаемое 1 2pv 2 где p плотность жидкости а скорость ее течения
Документальные учебные фильмы. Серия «Физика».
Даниил Бернулли (Daniel Bernoulli; 29 января (8 февраля) 1700 — 17 марта 1782), швейцарский физик-универсал, механик и математик, один из создателей кинетической теории газов, гидродинамики и математической физики. Академик и иностранный почётный член (1733) Петербургской академии наук, член Академий: Болонской (1724), Берлинской (1747), Парижской (1748), Лондонского королевского общества (1750). Сын Иоганна Бернулли.
Закон (уравнение) Бернулли является (в простейших случаях) следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

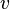
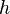
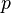
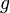
Уравнение Бернулли также может быть выведено как следствие уравнения Эйлера, выражающего баланс импульса для движущейся жидкости.
В научной литературе закон Бернулли, как правило, называется уравнением Бернулли(не следует путать с дифференциальным уравнением Бернулли), теоремой Бернулли или интегралом Бернулли.
Константа в правой части часто называется полным давлением и зависит, в общем случае, от линии тока.
Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Следует обратить внимание на то, что третье слагаемое по своему происхождению является работой сил давления и не представляет собой запаса какого-либо специального вида энергии («энергии давления»).
Соотношение, близкое к приведенному выше, было получено в 1738 г. Даниилом Бернулли, с именем которого обычно связывают интеграл Бернулли. В современном виде интеграл был получен Иоганном Бернулли около 1740 года.
Для горизонтальной трубы высота 
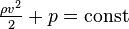
Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности 
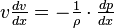
Согласно закону Бернулли, полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.
Полное давление состоит из весового 
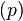

Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причиной эффекта Магнуса. Закон Бернулли справедлив и для ламинарных потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода расходомеров (например труба Вентури), водо- и пароструйных насосов. А последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины — гидравлики.
Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю. Для приближённого описания течений реальных жидкостей в технической гидромеханике (гидравлике) используют интеграл Бернулли с добавлением слагаемых, учитывающих потери на местных и распределенных сопротивлениях.
Известны обобщения интеграла Бернулли для некоторых классов течений вязкой жидкости (например, для плоскопараллельных течений), в магнитной гидродинамике, феррогидродинамике.
В статье были спользованны материалы Wikipedia
🎬 Видео
Уравнение Бернулли гидравликаСкачать

Уравнение БернуллиСкачать

Закон БернуллиСкачать

Вывод уравнений движения идеальной жидкости - Лекция 2Скачать

Уравнение Бернулли. Практическая часть. 10 класс.Скачать

Закон БернуллиСкачать

14. Движение идеальной жидкостиСкачать

Гидродинамика. Вывод уравнения БернуллиСкачать

10. Уравнения БернуллиСкачать

Уравнение Бернулли. Диаграмма Бернулли.Скачать

Закон Бернулли и движение по инерцииСкачать

Уравнение Бернулли Метод БернуллиСкачать

Уравнение Бернулли для потока жидкостиСкачать

Гидродинамика. Уравнение Бернулли. Физика 10 классСкачать

Уравнение Бернулли и его приложения | Гидродинамика, ГидравликаСкачать

#Дифуры I. Урок 8. Уравнение БернуллиСкачать

Основы гидродинамики и аэродинамики | уравнение БернуллиСкачать