- Ваш ответ
- решение вопроса
- Похожие вопросы
- Контрольная работа по физике Электромагнитные колебания и волны 11 класс
- 1 вариант
- 2 вариант
- 3 вариант
- 4 вариант
- 5 вариант
- X xmax cos wt формула
- Гармонические Колебания
- Гармонические колебания
- теория по физике 🧲 колебания и волны
- Уравнение движения гармонических колебаний
- Период и частота гармонических колебаний
- Зависимость частоты и периода свободных колебаний от свойств системы
- Фаза колебаний
- Превращение энергии при гармонических колебаниях
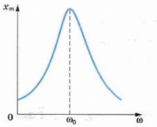
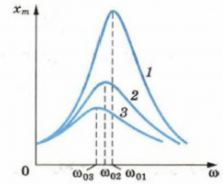
- Резонанс
- 📺 Видео
Видео:Урок 327. Гармонические колебанияСкачать

Ваш ответ
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

решение вопроса
Видео:График гармонического колебания | Алгебра 10 класс #23 | ИнфоурокСкачать

Похожие вопросы
- Все категории
- экономические 43,436
- гуманитарные 33,634
- юридические 17,907
- школьный раздел 608,233
- разное 16,858
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Контрольная работа по физике Электромагнитные колебания и волны 11 класс
Контрольная работа по физике Электромагнитные колебания и волны для учащихся 11 класса с ответами. Контрольная работа включает 5 вариантов, в каждом варианте по 8 заданий.
Видео:10 класс, 19 урок, График гармонического колебанияСкачать

1 вариант
A1. В уравнении гармонического колебания q = qmcos(ωt + φ0) величина, стоящая под знаком косинуса, называется
1) фазой
2) начальной фазой
3) амплитудой заряда
4) циклической частотой
А2. На рисунке показан график зависимости силы тока в металлическом проводнике от времени. Определите частоту колебаний тока.
1) 8 Гц
2) 0,125 Гц
3) 6 Гц
4) 4 Гц
А3. Как изменится период собственных электромагнитных колебаний в контуре, если ключ К перевести из положения 1 в положение 2?
1) Уменьшится в 2 раза
2) Увеличится в 2 раза
3) Уменьшится в 4 раза
4) Увеличится в 4 раза
А4. По участку цепи с сопротивлением R течёт переменный ток, меняющийся по гармоническому закону. В некоторый момент времени действующее значение напряжения на этом участке уменьшили в 2 раза, а его сопротивление уменьшили в 4 раза. При этом мощность тока
1) уменьшится в 4 раза
2) уменьшится в 8 раз
3) не изменится
4) увеличится в 2 раза
А5. Сила тока в первичной обмотке трансформатора 0,5 А, напряжение на её концах 220 В. Сила тока во вторичной обмотке 11 А, напряжение на её концах 9,5 В. Определите КПД трансформатора.
1) 105 %
2) 95 %
3) 85 %
4) 80 %
В1. В таблице показано, как изменялся заряд конденсатора в колебательном контуре с течением времени.
| t, 10 -6 с | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| q, 10 -6 Кл | 2 | 1,42 | 0 | -1,42 | -2 | -1,42 | 0 | 1,42 | 2 | 1,42 |
Вычислите ёмкость конденсатора в контуре, если индуктивность катушки равна 32 мГн. Ответ выразите в пикофарадах и округлите до десятых.
В2. Колебательный контур радиопередатчика содержит конденсатор ёмкостью 0,1 нФ и катушку индуктивностью 1 мкГн. На какой длине волны работает радиопередатчик? Скорость распространения электромагнитных волн с = 3 · 10 8 м/с. Ответ округлите до целых.
C1. Определите период электромагнитных колебаний в колебательном контуре, если амплитуда силы тока равна Im, а амплитуда электрического заряда на пластинах конденсатора qm.
Видео:Гармонические колебания | Физика 11 класс #8 | ИнфоурокСкачать

2 вариант
A1. В уравнении гармонического колебания i = Imcos(ωt + φ0) величина ω называется
1) фазой
2) начальной фазой
3) амплитудой силы тока
4) циклической частотой
А2. На рисунке показан график зависимости силы тока в металлическом проводнике от времени. Определите амплитуду колебаний тока.
1) 0,4 А
2) 0,2 А
3) 0,25 А
4) 4 А
А3. Как изменится частота собственных электромагнитных колебаний в контуре, если ключ К перевести из положения 1 в положение 2?
1) Уменьшится в 4 раза
2) Увеличится в 4 раза
3) Уменьшится в 2 раза
4) Увеличится в 2 раза
А4. По участку цепи с сопротивлением R течёт переменный ток, меняющийся по гармоническому закону. В некоторый момент времени действующее значение напряжения на этом участке увеличили в 2 раза, а сопротивление участка уменьшили в 4 раза. При этом мощность тока
1) не изменилась
2) возросла в 16 раз
3) возросла в 4 раза
4) уменьшилась в 2 раза
А5. Напряжение на концах первичной обмотки трансформатора 110 В, сила тока в ней 0,1 А. Напряжение на концах вторичной обмотки 220 В, сила тока в ней 0,04 А. Чему равен КПД трансформатора?
1) 120 %
2) 93 %
3) 80 %
4) 67 %
B1. Напряжение на конденсаторе в цепи переменного тока меняется с циклической частотой ω = 4000 с -1 . Амплитуда колебаний напряжения и силы тока равны соответственно Um = 200 В и Im = 4 А. Найдите ёмкость конденсатора.
В2. Найдите минимальную длину волны, которую может принять приёмник, если ёмкость конденсатора в его колебательном контуре можно плавно изменять от 200 пФ до 1800 пФ, а индуктивность катушки постоянна и равна 60 мкГн. Скорость распространения электромагнитных волн с = 3 · 10 8 м/с.
C1. В процессе колебаний в идеальном колебательном контуре в момент времени t заряд конденсатора q = 4 · 10 -9 Кл, а сила электрического тока в катушке равна I = 3 мА. Период колебаний Т = 6,28 · 10 -6 с. Найдите амплитуду колебаний заряда.
Видео:Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

3 вариант
А1. В уравнении гармонического колебания u = Umsin(ωt + φ0) величина φ0 называется
1) фазой
2) начальной фазой
3) амплитудой напряжения
4) циклической частотой
А2. На рисунке представлена зависимость силы тока в металлическом проводнике от времени.
Амплитуда колебаний тока равна
1) 20 А
2) 10 А
3) 0,25 А
4) 4 А
А3. В наборе радиодеталей для изготовления простого колебательного контура имеются две катушки с индуктивностями L1 = 1 мкГн и L2 = 2 мкГн, а также два конденсатора, ёмкости которых С1 = 3 пФ и С2 = 4 пФ. При каком выборе двух элементов из этого набора частота собственных колебаний контура будет наибольшей?
А4. По участку цепи сопротивлением R течёт переменный ток, меняющийся по гармоническому закону. Как изменится мощность переменного тока на этом участке цепи, если действующее значение напряжения на нём уменьшить в 2 раза, а его сопротивление в 4 раза увеличить?
1) Уменьшится в 16 раз
2) Уменьшится в 4 раза
3) Увеличится в 4 раза
4) Увеличится в 2 раза
А5. Напряжение на концах первичной обмотки трансформатора 127 В, сила тока в ней 1 А. Напряжение на концах вторичной обмотки 12,7 В, сила тока в ней 8 А. Чему равен КПД трансформатора?
1) 100 %
2) 90 %
3) 80 %
4) 70 %
B1. В таблице показано, как изменялся заряд конденсатора в колебательном контуре с течением времени.
| t, 10 -6 с | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| q, 10 -6 Кл | 0 | 2,13 | 3 | 2,13 | 0 | -2,13 | -3 | -2,13 | 0 | 2,13 |
Вычислите индуктивность катушки, если ёмкость конденсатора в контуре равна 100 пФ. Ответ выразите в миллигенри и округлите до целых.
В2. Найдите максимальную длину волны, которую может принять приёмник, если ёмкость конденсатора в его колебательном контуре можно плавно изменять от 200 пФ до 1800 пФ, а индуктивность катушки постоянна и равна 60 мкГн. Скорость распространения электромагнитных волн с = 3 · 10 8 м/с.
C1. В идеальном колебательном контуре амплитуда колебаний силы тока в катушке индуктивности равна 10 мА, а амплитуда колебаний заряда конденсатора равна 5 нКл. В момент времени t заряд конденсатора равен 3 нКл. Найдите силу тока в катушке в этот момент.
Видео:5.4 Уравнение гармонических колебанийСкачать

4 вариант
A1. В уравнении гармонического колебания u = Umsin(ωt + φ0) величина Um называется
1) фазой
2) начальной фазой
3) амплитудой напряжения
4) циклической частотой
А2. На рисунке представлена зависимость силы тока в металлическом проводнике от времени.
Частота колебаний тока равна
1) 0,12 Гц
2) 0,25 Гц
3) 0,5 Гц
4) 4 Гц
А3. На рисунке приведён график зависимости силы тока от времени в колебательном контуре при свободных колебаниях. Катушку в этом контуре заменили на другую катушку, индуктивность которой в 4 раза меньше. Каким будет период колебаний контура?
1) 1 мкс
2) 2 мкс
3) 4 мкс
4) 8 мкс
А4. По участку цепи с некоторым сопротивлением R течёт переменный ток, меняющийся по гармоническому закону. Как изменится мощность переменного тока на этом участке цепи, если действующее значение силы тока на нём увеличить в 2 раза, а его сопротивление в 2 раза уменьшить?
1) Не изменится
2) Увеличится в 2 раза
3) Уменьшится в 2 раза
4) Увеличится в 4 раза
А5. Напряжение на концах первичной обмотки трансформатора 220 В, сила тока в ней 1 А. Напряжение на концах вторичной обмотки 22 В. Какой была бы сила тока во вторичной обмотке при коэффициенте полезного действия трансформатора 100 %?
1) 0,1 А
2) 1 А
3) 10 А
4) 100 А
B1. Индуктивность катушки равна 0,125 Гн. Уравнение колебаний силы тока в ней имеет вид: i = 0,4cos(2 · 10 3 t), где все величины выражены в СИ. Определите амплитуду напряжения на катушке.
В2. Колебательный контур радиоприёмника содержит конденсатор, ёмкость которого 10 нФ. Какой должна быть индуктивность контура, чтобы обеспечить приём волны длиной 300 м? Скорость распространения электромагнитных волн с = 3 · 10 8 м/с.
C1. В идеальном колебательном контуре в катушке индуктивности амплитуда колебаний силы тока Im = 5 мА, а амплитуда колебаний заряда конденсатора qm = 2,5 нКл. В момент времени t сила тока в катушке i = 3 мА. Найдите заряд конденсатора в этот момент.
Видео:Как решить уравнение колебаний? | Олимпиадная физика, механические гармонические колебания, 11 классСкачать

5 вариант
A1. В уравнении гармонического колебания q = qmcos(ωt + φ0) величина, стоящая перед знаком косинуса, называется
1) фазой
2) начальной фазой
3) амплитудой заряда
4) циклической частотой
А2. На рисунке представлена зависимость силы тока в металлическом проводнике от времени.
Период колебаний тока равен
1) 2 мс
2) 4 мс
3) 6 мс
4) 10 мс
А3. На рисунке приведён график зависимости силы тока от времени в колебательном контуре при свободных колебаниях.
Если ёмкость конденсатора увеличить в 4 раза, то период собственных колебаний контура станет равным
1) 2 мкс
2) 4 мкс
3) 8 мкс
4) 16 мкс
А4. По участку цепи с некоторым сопротивлением R течёт переменный ток, меняющийся по гармоническому закону. В некоторый момент времени действующее значение силы тока на участке цепи увеличивается в 2 раза, а сопротивление уменьшается в 4 раза. При этом мощность тока
1) увеличится в 4 раза
2) увеличится в 2 раза
3) уменьшится в 2 раза
4) не изменится
А5. КПД трансформатора 90 %. Напряжение на концах первичной обмотки 220 В, на концах вторичной 22 В. Сила тока во вторичной обмотке 9 А. Какова сила тока в первичной обмотке трансформатора?
1) 0,1 А
2) 0,45 А
3) 0,9 А
4) 1 А
B1. В таблице показано, как изменялся заряд конденсатора в колебательном контуре с течением времени.
| t, 10 -6 с | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| q, 10 -6 Кл | 2 | 1,42 | 0 | -1,42 | -2 | -1,42 | 0 | 1,42 | 2 | 1,42 |
Вычислите индуктивность катушки, если ёмкость конденсатора в контуре равна 50 пФ. Ответ выразите в миллигенри и округлите до целых.
В2. Электрический колебательный контур радиоприёмника содержит катушку индуктивности 10 мГн и два параллельно соединенных конденсатора, ёмкости которых равны 360 пФ и 40 пФ. На какую длину волны настроен контур? Скорость распространения электромагнитных волн с = 3 · 10 8 м/с.
C1. В идеальном колебательном контуре амплитуда колебаний силы электрического тока в катушке индуктивности Im = 5 мА, а амплитуда напряжения на конденсаторе Um = 2 В. В момент времени t сила тока в катушке i = 3 мА. Найдите напряжение на конденсаторе в этот момент.
Ответы на контрольную работу по физике Электромагнитные колебания и волны 11 класс
1 вариант
1-1
2-2
3-1
4-3
5-2
6. 50,7 пФ
7. 18,84 м
8. T = 2πqm/Im
2 вариант
1-4
2-2
3-3
4-2
5-3
6. 5 мкФ
7. 206,4 м
8. 5 нКл
3 вариант
1-2
2-2
3-3
4-1
5-3
6. 65 мГн
7. 619,1 м
8. 8 мА
4 вариант
1-3
2-2
3-2
4-2
5-3
6. 100 В
7. 2,54 мкГн
8. 2 нКл
5 вариант
1-3
2-2
3-3
4-4
5-4
6. 32 мГн
7. 3768 м
8. 1,6 В
Видео:Физика 9 класс (Урок№11 - Гармонические колебания. Затухающие колебания. Резонанс.)Скачать

X xmax cos wt формула
Механические волны
Е) Вынужденные колебания. Резонанс.
Гармонические колебания
План лекции
Механические колебания и волны.
ЛЕКЦИЯ 1
а) Общая характеристика и уравнение колебательного движения
б) Баланс энергии при колебательном движении
в) Сложение гармонических колебаний
г) Гармонический спектр простого и сложного колебания
д) Затухающие колебания
а) Общая характеристика волны. Волны продольные и поперечные.
б) Уравнение плоской волны
в) Поток энергии волны. Уравнение Умова.
а) Общая характеристика и уравнение колебательного движения.
Колебательное движение – один из видов механического движения. В жизни оно встречается повсюду: маятник в настенных часах, груз, подвешенный на пружине, вода в открытом сосуде, вагон на рессорах, корабль на волнах и др. Главной характерной чертой колебательного движения является егоповторяемость,т.е. каждое последующее движение повторяет предыдущее.
Для осуществления колебательного движения необходимы следующие условия: во-первых, должно быть наличие инертной массы, во-вторых, при выведении тела из положения равновесия должна возникать возвращающая сила.Данная сила должна быть пропорциональна величине отклонения тела от положения равновесия. Данная сила сообщает телу ускорение.
F = -kX– сила упругости; F = ma– сила инерции.
В данном случае, сила упругости является силой инерции: ma = -kX
Отсюда: a = -(k/m)XВведём обозначение: k/m = w 2 Здесь w– циклическая частота колебаний. Перепишем это уравнение в виде:
d 2 X/dt 2 = -w 2 X
Это – дифференциальное уравнение 2-го порядка. Представим его в виде:
d 2 X/dt 2 + w 2 X = 0
где d 2 X/dt 2 = kX/m w = k/m
Частное решение этого уравнения будет выглядеть так:
X = A sin ( wt + fо)
X – текущая координата
A – амплитуда
w – циклическая частота
t – время
f – фаза
fо – начальная фаза.
Следует напомнить, что здесь, как и во всей физике принято координату и амплитуду измерять в метрах, время – в секундах, фазу – в радианах, циклическую частоту – в с -1 .
Кроме того, в физике колебательного движения приняты следующие единицы:
n– частота (Гц)
Т – период (с)
Частота (в герцах) показывает, сколько колебаний совершит тело за 1 секунду.
Частота w ( в с -1 ) показывает, сколько колебаний тело совершит за 2pсекунд.
Период Т показывает продолжительность одного полного колебания (в секундах)
Особенность колебательного движения в том, что его легко можно связать с вращательным. Если представить себе какое-либо тело, движущееся по окружности в плоскости чертежа, то тень от него, падающая на вертикальную ось координат Х, будет совершать колебания вверх-вниз и если развернуть это движение на горизонтальную ось t, то получится кривая, являющаяся синусоидой.
Следует заметить, что графиком частного решения вышеуказанного дифференциального уравнения является кривая той же формы:
Наибольшее затруднение у студентов вызывает понятие фазы. В колебательном движении фаза играет туже роль, что координата в поступательном движении.
X = (ut + X ) для поступательного движения
f = ( wt + f ) для колебательного движения
В колебательном движении фаза показывает, какая часть периода прошла от начала колебания.
Зная, что координата колеблющегося тела изменяется по закону:
Х = А sin (wt + f )
найдём закон, по которому изменяется скорость и ускорение:
u = X = A w cos(wt + f )
a = u = X = -Aw 2 sin (wt + f )
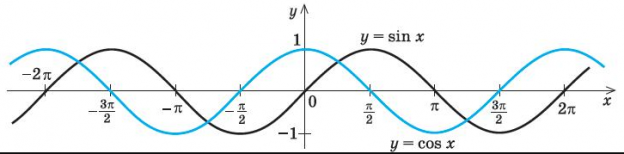
Отсюда видно, что координата, скорость и ускорение изменяются либо по закону синуса, либо по закону косинуса. Причём, производная любого порядка даст либо синус, либо косинус. Из этого следует, что синус и косинус являются гармоническими функциями. Значит движение, осуществляющееся по законам синуса или косинуса является гармоническим колебанием, или колебанием, типа «проще некуда».
Все эти три графика представляют собой кривую одинаковой формы, только эти кривые сдвинуты относительно друг друга на 90 о
б) Баланс энергии при колебательном движении
Следует напомнить формулы кинетической и потенциальной энергии, используемые в механике.
Ек = mu 2 /2 – кинетическая энергия
Еп = kX 2/ /2 – потенциальная энергия
Из закона сохранения энергии следует, что полная механическая энергия замкнутой системы – есть величина постоянная:
Ек + Еп = Е
u = dX/dt = ( A sin wt) = A cos wt u = Aw
a = d 2 X/dt 2 = du/dt (Acos wt) = -Aw 2 sin wt a = Aw 2
Кинетическая энергия точки:
Ek = mA 2 cos 2 w t
Потенциальная энергия точки:
Еп = kA 2 /2 здесь: k = m w 2 так как k = ma /X = mA 2 w 2 /X
Еп =mA 2 w 2 sin 2 w t
Ек = mA 2 w 2 sin 2 w t
2
Ек + Еп = mA 2 w 2 (sin 2 wt + cos 2 wt)
Учитывая, что выражение в скобках равно единице, окончательно получим значение полной механической энергии колеблющейся точки
Е = mA 2 w 2
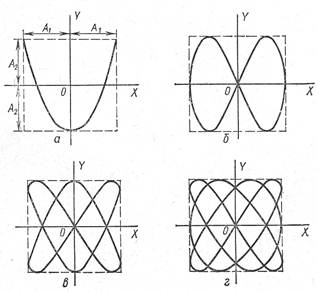
в) Сложение гармонических колебаний
Гармонические колебания можно сложить как в одном направлении, так и во взаимно перпендикулярных направлениях. Рассмотрим сложение колебаний в одном направлении. Возьмём простейший случай, когда складываются колебания одинаковой частоты, совпадающих по фазе. В этом случае будут складываться их амплитуды:
Если складываются колебания, находящиеся в противофазе, то их амплитуды будут вычитаться. При одинаковых амплитудах, колебания вообще погасят друг друга:
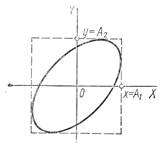
Если колебания складываются во взаимно перпендикулярном направлении, то колеблющаяся точка будет на плоскости выписывать сложную траекторию. Если частоты этих колебаний будут относиться как целые числа, то траектория будет иметь вид устойчивой кривой, которая называется фигурой Лиссажу:
г) Гармонический спектр
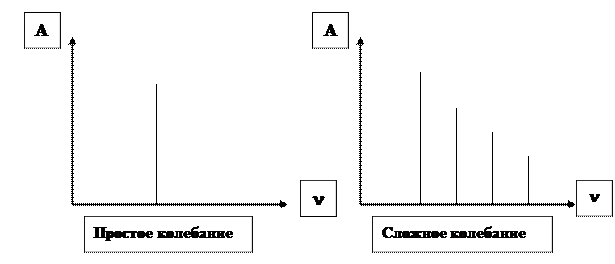
Если в одном направлении складываются колебания разных частот, то точка будет совершать сложные колебания, график которых будет представлять очень замысловатый вид, изобразить который графически бывает очень трудно. Существует ещё один способ графического изображения колебательного движения.
Французский математик Фурье доказал, что периодический процесс любой формы можно разложить на простые гармонические колебания. В связи с этим, графически колебания можно изобразить гармоническим спектром. По горизонтальной оси откладывается частота, а по вертикальной – амплитуда. Таким образом, гармонический спектр простого синусоидального колебания представляет собой отрезок прямой, перпендикулярный оси частот. Положение отрезка по горизонтали определяется частотой, а длина отрезка – амплитудой колебания.
Спектр сложного колебания представляет собой несколько линий.
Во многих случаях колебания изображать гармоническим спектром удобнее и проще, чем их графиком.
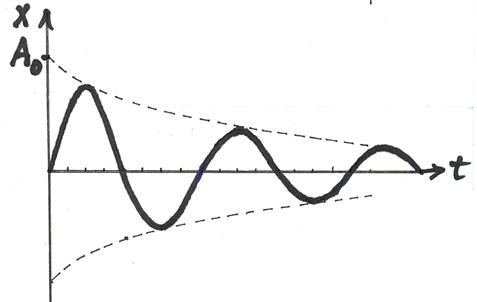
д) Затухающие колебания
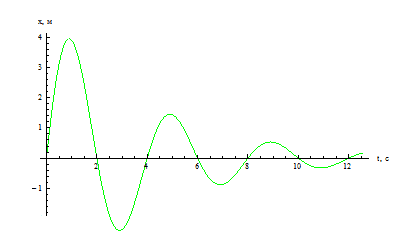
В идеальном случае в колебательной системе происходит обмен кинетической и потенциальной энергии, причём, потерь энергии на трение нет. Поэтому, амплитуда колебания остаётся постоянной. В реальных же условиях при каждом цикле часть энергии переходит во внутреннюю, поэтому амплитуда колебания постепенно уменьшается по экспоненциальному закону:
Х = Aoe – bt sinwt гдe b– коэффициент затухания
График затухающего колебания имеет вид:
Дата добавления: 2014-01-05 ; Просмотров: 3739 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Ответ оставил Гость
Решение: 1. запишем уровнение гк – X = Xmax * cos (wt + Фи(0)
2. выразим Омегу (w) через период (Т) : w = 2Пи/ T => w = 4*2Пи/10 = 4Пи/5 или
6.28 / 2.4 = 2,616. 7
3. подставляем в уравнение Х = 0.05*cos(4Пи/5 * 0.6)
Видео:Физика. 11 класс. Уравнение и графика гармонических колебаний /03.09.2020/Скачать

Гармонические Колебания
Механическое гармоническое колебание – это прямолинейное неравномерное движение, при котором координаты колеблющегося тела (материальной точки) изменяются по закону косинуса или синуса в зависимости от времени.
Согласно этому определению, закон изменения координаты в зависимости от времени имеет вид:

Уравнения (4.1) являются основными кинематическими уравнениями механических гармонических колебаний.
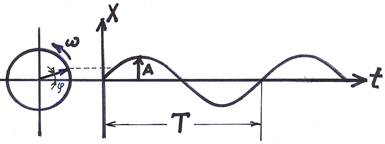
Рассмотрим следующий пример. Возьмем ось Ох (рис. 64). Из точки 0 проведем окружность с радиусом R = А. Пусть точка М из положения 1 начинает двигаться по окружности с постоянной скоростью v (или с постоянной угловой скоростью w , v = wА ). Через некоторое время t радиус повернется на угол ф: ф=wt .
При таком движении по окружности точки М ее проекция на ось х М х будет совершать движение вдоль оси х, координата которой х будет равна х = А • cos ф = = А • cos wt . Таким образом, если материальная точка движется по окружности радиусом А, центр которой совпадает с началом координат, то проекция этой точки на ось х (и на ось у) будет совершать гармонические механические колебания.
Если известна величина wt, которая стоит под знаком косинуса, и амплитуда А, то можно определить и х в уравнении (4.1).
Величину wt, стоящую под знаком косинуса (или синуса), однозначно определяющую координату колеблющейся точки при заданной амплитуде, называют фазой колебания . Для точки М, движущейся по окружности, величина w означает ее угловую скорость. Каков физический смысл величины w для точки М х , совершающей механические гармонические колебания? Координаты колеблющейся точки М х одинаковы в некоторый момент времени t и (Т +1) (из определения периода Т), т. е. A cos wt = A cos w (t + Т), а это значит, что w (t + Т) – wt = 2 ПИ (из свойства периодичности функции косинуса). Отсюда следует, что
Следовательно, для материальной точки, совершающей гармонические механические колебания, величину w можно интерпретировать как количество колебаний за определенный цикл времени, равный 2л . Поэтому величину w назвали циклической (или круговой) частотой .
Если точка М начинает свое движение не из точки 1 а из точки 2, то уравнение (4,1) примет вид:
Величину ф 0 называют начальной фазой .
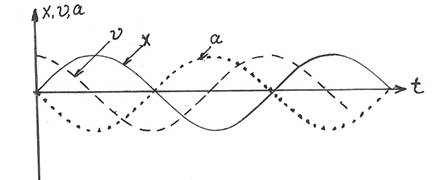
Скорость точки М х найдем как производную от координаты по времени:
Ускорение точки, колеблющейся по гармоническому закону, определим как производную от скорости:
Из формулы (4.4) видно, что скорость точки, совершающей гармонические колебания, изменяется тоже по закону косинуса. Но скорость по фазе опережает координату на ПИ/2 . Ускорение при гармоническом колебании изменяется по закону косинуса, но опережает координату по фазе на п . Уравнение (4.5) можно записать через координату х:
Ускорение при гармонических колебаниях пропорционально смещению с противоположным знаком. Умножим правую и левую части уравнения (4.5) на массу колеблющей материальной точки т, получим соотношения:
Согласно второму закону Ньютона, физический смысл правой части выражения (4.6) есть проекция силы F x , которая обеспечивает гармоническое механическое движение:
Величина F x пропорциональна смещению х и направлена противоположно ему. Примером такой силы является сила упругости, величина которой пропорциональна деформации и противоположно ей направлена (закон Гука).
Закономерность зависимости ускорения от смещения, вытекающую из уравнения (4.6), рассмотренную нами для механических гармонических колебаний, можно обобщить и применить при рассмотрении колебаний другой физической природы (например, изменение тока в колебательном контуре, изменение заряда, напряжения, индукции магнитного поля и т. д.). Поэтому уравнение (4.8) называют основным уравнением динамики гармонических колебаний .
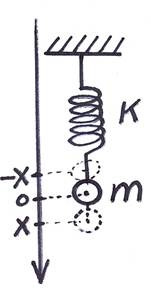
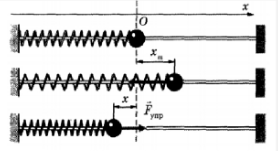
Рассмотрим движение пружинного и математического маятников.
Пусть к пружине (рис. 63), расположенной горизонтально и закрепленной в точке 0, одним концом прикреплено тело массой т, которое может перемещаться вдоль оси х без трения. Коэффициент жесткости пружины пусть будет равен k. Выведем тело m внешней силой из положения равновесия и отпустим. Тогда вдоль оси х на тело будет действовать только упругая сила, которая согласно закону Гука, будет равна: F yпp = -kx.
Уравнение движения этого тела будет иметь вид:
Сравнивая уравнения (4.6) и (4.9), делаем два вывода:
- Движение тела на пружине будет происходить по гармоническому закону, т. е. тело m будет совершать механические гармонические колебания;
- Сравнивая коэффициенты перед х уравнений (4.6) и (4.9), заключаем, что циклическая частота этих гармонических колебаний будет равна:
Из формул (4.2) и (4.10) выводим формулу для периода колебаний груза на пружине:
Математическим маятником называется тело массой т, подвешенное на длинной нерастяжимой нити пренебрежимо малой массы. В положении равновесия на это тело будут действовать сила тяжести и сила упругости нити. Эти силы будут уравновешивать друг друга.
Если нить отклонить на угол а от положения равновесия, то на тело действуют те же силы, но они уже не уравновешивают друг друга, и тело начинает двигаться по дуге под действием составляющей силы тяжести, направленной вдоль касательной к дуге и равной mg sin a .
Уравнение движения маятника принимает вид:
Знак минус в правой части означает, что сила F x = mg sin a направлена против смещения. Гармоническое колебание будет происходить при малых углах отклонения, т. е. при условии а 2* sin a .
Заменим sin а в уравнении (4.12), получим следующее уравнение:
Уравнение (4.13) показывает, что ускорение колебания маятника прямо пропорционально смещению и противоположно ему направлено. Следовательно, маятник будет совершать механические гармонические колебания с циклической частотой
и поэтому, согласно уравнению (4.2), период колебаний его будет равен:
Превращение энергии при гармонических механических колебаниях рассмотрим на примере пружинного маятника. В любой момент времени полная энергия колеблющегося груза (Е полн ) будет состоять из кинети-
Полная энергия при гармонических механических колебаниях пропорциональна квадрату амплитуды и квадрату циклической частоты.
На рис. 65 качественно изображены графики зависимостей потенциальной и кинетической энергии пружинного маятника от координаты х.
На рис. 66 представлены качественные графики зависимостей кинетической и потенциальной энергии от времени.
За начальный момент времени принято положение тела, максимально отклоненное от положения равновесия. Частота колебания потенциальной и кинетической энергии в два раза больше, чем частота колебания движущегося тела.
Видео:Тема 1. Колебательное движение. Гармонические колебания. Уравнение гармонических колебанийСкачать

Гармонические колебания
теория по физике 🧲 колебания и волны
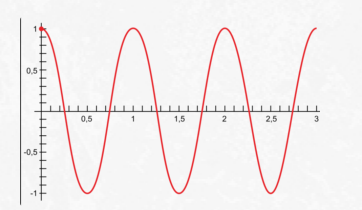
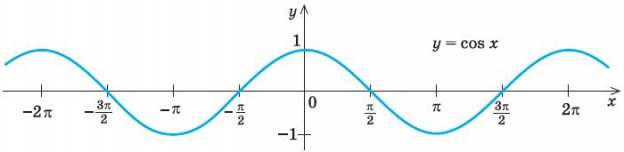
Гармоническими законами называют законы синуса и косинуса. Следовательно, гармоническими колебаниями называют те колебания, при которых координата тела изменяется синусоидально или косинусоидально.
Гармонические колебания — колебания, при которых координата тела изменяется с течением времени по гармоническому закону.
Ниже представлен график косинусоидальной функции. Обратите внимание, что косинус при возрастании аргумента от нуля сначала меняется медленно, а потом он все быстрее и быстрее приближается к нулю. Пройдя через него, его модуль снова быстро возрастает. Но по мере приближения к максимальному значению он снова замедляется. Точно так же меняются координаты свободно колеблющегося тела.
Важно! Гармоническими можно считать только те колебания, что совершаются грузом, закрепленном на пружине, или математическим маятником, отклоняемым на малый угол, при котором ускорение тела пропорционально его смещению.
Видео:Гармонические колебанияСкачать

Уравнение движения гармонических колебаний
Известно, что ускорение колеблющегося на пружине груза пропорционально его смещению от положения равновесия:
Также известно, что ускорение есть вторая производная координаты. Следовательно, при свободных колебаниях координата изменяется со временем так, что вторая производная координаты по времени прямо пропорциональна самой координате и противоположна ей по знаку.
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
x″ = − x m a x cos . t = − x
Видно, что в этом случае теряется величина k m . . , служащая постоянной для каждой колебательной системы. Чтобы получить ее во второй производной, нужно усложнить функцию до следующего вида:
x = x m a x cos . √ k m . . t
Тогда первая производная примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
x′ = − √ k m . . x m a x sin . √ k m . . t
Вторая производная примет вид:
x″ = − k m . . x m a x cos . √ k m . . t = − k m . . x
Так как мы получили ровно такое же выражение, то описать свободные колебания можно уравнениями следующего вида:
x = x m a x sin . √ k m . . t
x = x m a x cos . √ k m . . t
Обозначим постоянную величину √ k m . . , зависящую от свойств системы, за ω0:
x = x m a x sin . ω 0 t
x = x m a x cos . ω 0 t
Само уравнение движения, описывающего свободные колебания, примет вид:
Видео:Урок 329. Задачи на гармонические колебания - 1Скачать

Период и частота гармонических колебаний
Минимальный промежуток времени T, через который движение тела полностью повторяется, называют периодом колебания. Зная его, можно вычислить частоту колебаний, равную числу колебаний в единицу времени. Эти величины связаны между собой выражением:
Через промежуток времени, равный периоду T и соответствующий изменению аргумента косинуса на ω 0 T , движение тела повторяется, и косинус принимает прежнее значение. Но из математики известно, что наименьший период косинуса равен 2π. Следовательно:
ω 0 = 2 π T . . = 2 π ν
Таким образом, величина ω 0 представляет собой число колебаний тела, но не за 1 секунду, а за 2 π секунд. Эта величина называется циклической (круговой) частотой. А частоту свободных колебаний называют собственной частотой колебательной системы.
Видео:Гармонические колебания. Физика 11 классСкачать

Зависимость частоты и периода свободных колебаний от свойств системы
Изначально за величину ω 0 мы принимали постоянную, характеризующую свойства системы:
Теперь мы выяснили, что циклическая частота связана с периодом и частотой колебаний. Следовательно, период и частота колебаний также зависят от свойств системы:
ω 0 = √ k m . . = 2 π T . . = 2 π ν
Отсюда период и частота колебаний соответственно равны:
T = 2 π ω 0 . . = 2 π √ m k . .
ν = 1 2 π . . √ k m . .
Вспомним, что свойства колебательной системы математического маятника определяются постоянной величиной g l . . . Следовательно, циклическая частота для него равна:
Отсюда период и частота колебаний математического маятника соответственно равны:
T = 2 π ω 0 . . = 2 π √ l g . .
ν = 1 2 π . . √ g l . .
Эта формула была впервые получена и проверена на опыте голландским ученым Г. Гюйгенсом, современником И. Ньютона.
Период колебания возрастает с увеличением длины маятника. От массы маятника он не зависит. Это легко проверить на опыте с различными маятниками. Зависимость периода от ускорения свободного падения также легко прослеживается. Чем меньше величина g, тем больше период колебания маятника, и, следовательно, тем медленнее идут часы с маятником. Так, часы с маятником в виде груза на стержне отстанут в сутки почти на 3 с, если их поднять из подвала на верхний этаж Московского университета, который находится на высоте 200 м. И это только за счет уменьшения ускорения свободного падения с высотой.
Зависимость периода колебаний маятника от значения g используется на практике. Измеряя период колебания, можно легко измерить g. Ускорение свободного падения меняется с географической широтой. Но и на данной широте оно неодинаково, так как плотность земной коры неоднородна. В районах, где залегают более плотные породы, ускорение свободного падения принимает большие значения.
Пример №1. Сколько колебаний совершает математический маятник длиной 4,9 м за время 5 минут?
Искомое число колебаний равно отношению времени к периоду колебаний:
Период колебаний для математического маятника определяется формулой:
N = t 2 π . . √ g l . . = 300 2 · 3 , 14 . . √ 9 , 8 4 , 9 . . ≈ 68
Видео:Физика ЦТ | Механические колебания. Часть1. Уравнение колебаний гармонического осциллятораСкачать

Фаза колебаний
При заданной амплитуде гармонических колебаний координата колеблющегося тела в любой момент времени однозначно определяется аргументом косинуса или синуса, который равен ω 0 t . Обозначим его за ϕ и получим:
Величину ϕ, стоящую под знаком косинуса или синуса, называют фазой колебаний, описываемой этой функцией. Выражается фаза в угловых единицах — радианах (рад).
Фаза определяет значение не только координаты, но и других физических величин (к примеру, скорости и ускорения, которые также изменяются по гармоническому закону). Отсюда можно сделать вывод, что фаза определяет при заданной амплитуде состояния колебательной системы в любой момент времени.
Колебания с одинаковыми частотами и амплитудами могут отличаться друг от друга фазами. Так как ω 0 = 2 π T . . , фаза определяется формулой:
ϕ = ω 0 t = 2 π t T . .
t T . . — отношение, которое указывает, какая часть периода прошла от момента начала колебаний. Любому моменту времени, выраженному в долях периода, соответствует значение фазы, выраженное в радианах. К примеру:
| Время, t (с) | 0 |
| Фаза, ϕ (рад) | 0 |