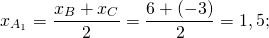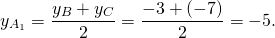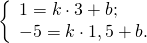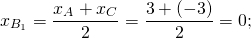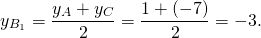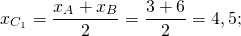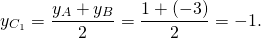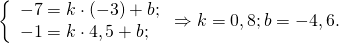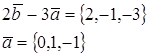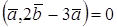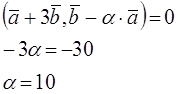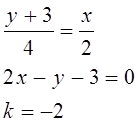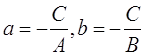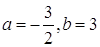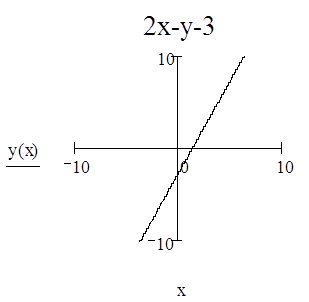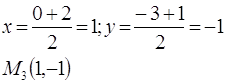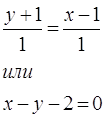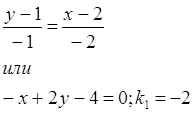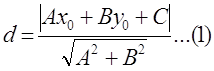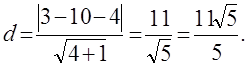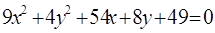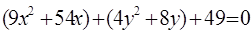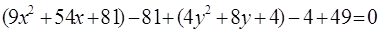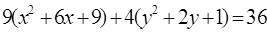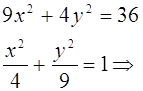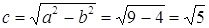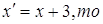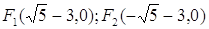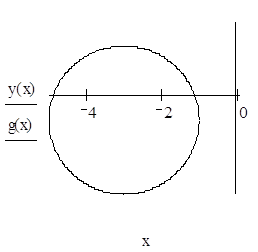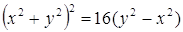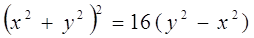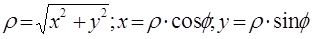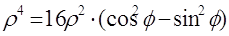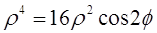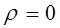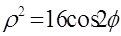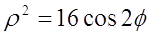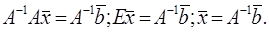Как составить уравнение медианы треугольника по координатам его вершин?
Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:
- Найти координаты середины отрезка по координатам его концов.
- Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.
Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).
Найти уравнения медиан треугольника.
Обозначим середины сторон BC, AC, AB через A1, B1, C1.
Уравнение медианы AA1 будем искать в виде y=kx+b.
Найдём уравнение прямой, проходящей через точки A(3;1) и A1(1,5;-5). Составляем и решаем систему уравнений:
Отсюда k= 4; b= -11.
Уравнение медианы AA1: y=4x-11.
2) Аналогично, координаты точки B1 — середины отрезка AC
Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B1(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы BB1 можно найти ещё быстрее: y= -3.
3) Координаты точки C1 — середины отрезка BC:
Отсюда уравнение медианы CC1 : y=0,8x-4,6.
Видео:Вычисление медианы, высоты и угла по координатам вершинСкачать
Краткие сведения и задачи по курсу векторной и линейной алгебры
Краткие сведения и задачи по курсу векторной и линейной алгебры
1. Найти скалярное произведение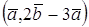 
.
2. При каком значении α векторы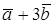 
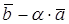
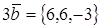
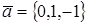
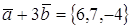
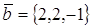
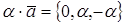
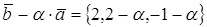
и 
ортогональны?
;
;
;
;
;
;
Два вектора ортогональны, когда их скалярное произведение равно нулю.
3. Для прямой М1М2 написать уравнение с угловым коэффициентом, в отрезках и общее уравнение. Начертить график прямой. М1(0,-3) М2(2,1).
Общий вид уравнения прямой с угловым коэффициентом записывается в виде:
Общий вид уравнения прямой, проходящей через две точки записывается в виде:
,
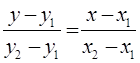
Общий вид уравнения прямой в отрезках записывается в виде:
,
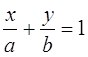
Уравнения прямой в отрезках для прямой М1М2
;
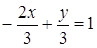
4. В треугольнике М0М1М2 найти уравнение медианы, высоты, проведенных их вершины М0, а также уравнение средней линии EF, параллельной основанию М1М2.(М0(-1,-2); М1(0,-3); М2(2,1)).
Найдём координаты точки М3, координаты середины стороны М1М2:
уравнения прямой, проходящей через две точки записывается в виде:
,
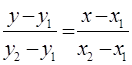
Найдём уравнение прямой М1М2:
Из условия перпендикулярности (k2=-1/k1) следует, что k2=1/2.
Уравнения прямой с угловым коэффициентом записывается в виде:
тогда уравнение для высоты примет вид:
Расстояние от точки М(x0,y0) до прямой Ax+By+c=0 находится по формуле:
Чтобы найти длину высоту, найдём расстояние от точки М0(-3,-5) до прямойМ1М2, уравнение которой имеет вид -x+2y-4=0. Подставим данные в формулу(1):
Найдём координаты точек Е иF.
Для точки Е: x=-1/2; y=-5/2; E(-1/2;-5/2).
Для точки F: x=1/2; y=-1/2; F(1/2;-1/2).
Уравнение прямой EF:
y+5/2=-2x-1 или 2x+y+3,5=0.
5. По каноническому уравнению кривой второго порядка определить тип кривой, начертить её график. Найти координаты фокусов, вершин и центра (для центральной кривой).
(1)
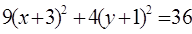
Воспользуемся параллельным переносом (O’(-3,-1))
(2)
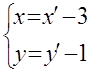
Подставим (2) в (1), получим
кривая второго порядка является эллипсом.
т.к.
Координаты центра: O’(-3,-1).
6. Преобразовать к полярным координатам уравнения линии.
1)
2) 
Первое уравнение представляет собой (при любых значениях φ) полюс О. Второе – дает все точки линии, в том числе полюс. Поэтому первое уравнение можно отбросить. Следовательно, получаем:
Ответы на вопросы
1. Дайте определение обратной матрицы. Какие вы знаете способы вычисления обратной матрицы?
Матрица В называется обратной для матрицы А, если выполняется условие АВ=ВА=Е, где Е – единичная матрица. Способы вычисления обратной матрицы: 1) использование алгебраических дополнений; 2) привести исходную матрицу к ступенчатому виду методом Гаусса, после чего необходимо преобразовать её в единичную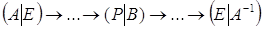 
.
2. Как записывается система уравнений в матрично-векторной форме? Как найти решение системы уравнений при помощи обратной матрицы?
Система уравнений в матрично-векторной форме записывается в виде: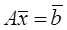 
.
Решение системы уравнения при помощи обратной матрицы:
3. Сформулируйте, в чем состоит процедура Гаусса и для решения каких линейных задач применяется?
Процедура Гаусса используется для решения систем линейных уравнений и состоит в следующем:
Выполняются элементарные преобразования, вследствие чего можно получить два исхода:
Видео:Вычисляем высоту через координаты вершин 1Скачать
В треугольнике м1 м2 м3 найти уравнение медианы высоты проведенных из вершины м1
Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет — тут
Неправильный логин или пароль.
Укажите электронный адрес и пароль.
Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.
Инструкция по изменению пароля отправлена на почту.
Чтобы зарегистрироваться, укажите ваш email и пароль
Нажимая кнопку «Зарегистрироваться» вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.
Видео:Уравнения стороны треугольника и медианыСкачать
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. 🎦 Видео№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать  Задача 7. Найти расстояние от точки M0 до плоскости, проходящей через три точки M1, M2, M3.Скачать  7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать  Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать  найти уравнение высоты треугольникаСкачать  №973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать  Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать  Аналитическая геометрия на плоскости. Решение задачСкачать  Уравнение медианыСкачать  Уравнение прямой и треугольник. Задача про высотуСкачать  Математика без Ху!ни. Смешанное произведение векторовСкачать  Математика без Ху!ни. Уравнение плоскости.Скачать  Формулы для медианы треугольникаСкачать  Аналитическая геометрия, 6 урок, Уравнение прямойСкачать  Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать  найти уравнения биссектрис углов между прямымиСкачать  Найдите площадь треугольника, если его медианы равны 3, 4 и 5Скачать  | ||