Про уравнения - легко » Статьи

В трансцендентном уравнении функции f и g является аналитические функции

Обновлено
Трансцендентные функции: типы, определение, свойства, примеры

Трансцендентные функции: типы, определение, свойства, примеры — Наука

Содержание
  1. Содержание:
  2. Определение и свойства
  3. Экспоненциальная функция
  4. Свойства экспоненциальной функции
  5. Функции синуса, косинуса и тангенса
  6. Производные и интегралы
  7. Производная экспоненциальной функции
  8. Интеграл от экспоненциальной функции
  9. Таблица производных и интегралов трансцендентных функций
  10. Примеры
  11. Пример 1
  12. Пример 2
  13. Ссылки
  14. 63. Основные трансцендентные функции
  15. Трансцендентная функция — аналитическая функция, не являющаяся алгебраической
  16. Трансцендентные функции
  17. Примеры решения, формулы и задачи
  18. 🎬 Видео

Видео:Понятие функции. 7 класс.Скачать

Понятие функции. 7 класс.

Содержание:

Втрансцендентные функции Элементарными являются экспоненты, логарифмические, тригонометрические, обратные тригонометрические функции, гиперболические и обратные гиперболические функции. То есть они не могут быть выражены с помощью многочлена, частного многочленов или корней многочленов.

Неэлементарные трансцендентные функции также известны как специальные функции, и среди них может быть названа функция ошибок. В алгебраические функции (многочлены, частные от многочленов и корни многочленов) вместе с трансцендентные функции элементалы составляют то, что в математике известно как элементарные функции.

Трансцендентными функциями также считаются те, которые возникают в результате операций между трансцендентными функциями или между трансцендентными и алгебраическими функциями. Этими операциями являются: сумма и разность функций, произведение и частное функций, а также композиция двух или более функций.

Видео:Функция. Область определения функции. Практическая часть. 10 класс.Скачать

Функция. Область определения функции. Практическая часть. 10 класс.

Определение и свойства

Видео:Способы задания функции. 10 класс.Скачать

Способы задания функции. 10 класс.

Экспоненциальная функция

Это действительная функция действительной независимой переменной вида:

где к положительное действительное число (а> 0) исправлено называется базой. Циркумфлекс или надстрочный индекс используются для обозначения операции потенцирования.

Скажем а = 2 тогда функция выглядит так:

f (x) = 2 ^ х = 2 Икс

Что будет оцениваться для нескольких значений независимой переменной x:

Ниже приведен график, на котором экспоненциальная функция представлена ​​для нескольких значений базы, включая базовую. а также (Непер число а также ≃ 2.72). Основание а также настолько важен, что, когда мы говорим об экспоненциальной функции, мы думаем о e ^ x, который также обозначается ехр (х).

Видео:9 класс, 15 урок, Определение числовой функции. Область определения, область значения функцииСкачать

9 класс, 15 урок, Определение числовой функции. Область определения, область значения функции

Свойства экспоненциальной функции

Из рисунка 1 видно, что область значений экспоненциальных функций — это действительные числа (Dom f = р), а диапазон или диапазон — положительные числа (Ran f = р + ).

С другой стороны, независимо от значения основания a, все экспоненциальные функции проходят через точку (0, 1) и через точку (1, a).

Когда база а> 1, то функция возрастает и при 0 1), функция логарифма возрастает. Но если (0

Видео:Как найти область определения функции? #shortsСкачать

Как найти область определения функции? #shorts

Функции синуса, косинуса и тангенса

Функция синуса присваивает каждому значению x действительное число y, где x представляет собой меру угла в радианах. Чтобы получить значение Sen (x) угла, угол представлен в единичном круге, а проекция указанного угла на вертикальную ось представляет собой синус, соответствующий этому углу.

Тригонометрический круг и синус для различных угловых значений X1, X2, X3 и X4 показаны ниже (на рисунке 3).

Определенное таким образом максимальное значение, которое может иметь функция Sen (x), равно 1, что происходит, когда x = π / 2 + 2π n, где n — целое число (0, ± 1, ± 2,). Минимальное значение, которое может принимать функция Sen (x), происходит, когда x = 3π / 2 + 2π n.

Функция косинуса y = Cos (x) определяется аналогичным образом, но проекция угловых положений P1, P2 и т.д. осуществляется на горизонтальную ось тригонометрической окружности.

С другой стороны, функция y = Tan (x) представляет собой частное между функцией синуса и функцией косинуса.

Ниже представлен график трансцендентных функций Sen (x), Cos (x) и Tan (x).

Видео:Функция. Область определения и область значения функции. Алгебра, 9 классСкачать

Функция. Область определения и область значения функции. Алгебра, 9 класс

Производные и интегралы

Видео:Тригонометрические функции, y=tgx и y=ctgx, их свойства и графики. 10 класс.Скачать

Тригонометрические функции, y=tgx и y=ctgx, их свойства и графики. 10 класс.

Производная экспоненциальной функции

Производная Y ‘ экспоненциальной функции у = а ^ х это функция а ^ х умноженный на натуральный логарифм основания a:

y ’= (a ^ x)’ = a ^ x ln a

В частном случае базы а также, производная экспоненциальной функции является самой экспоненциальной функцией.

Видео:Обратная функция. 10 класс.Скачать

Обратная функция. 10 класс.

Интеграл от экспоненциальной функции

Неопределенный интеграл от а ^ х — это сама функция, деленная на натуральный логарифм основания.

В частном случае основания e интеграл экспоненциальной функции является самой экспоненциальной функцией.

Видео:ТФКП. Восстановление аналитической функции по ее известной действительной частиСкачать

ТФКП. Восстановление аналитической функции по ее известной действительной части

Таблица производных и интегралов трансцендентных функций

Ниже представлена ​​сводная таблица основных трансцендентных функций, их производных и неопределенных интегралов (первообразных):

Видео:01. Что такое функция в математикеСкачать

01. Что такое функция в математике

Примеры

Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график Парабола

Пример 1

Найдите функцию, полученную в результате композиции функции f (x) = x ^ 3 с функцией g (x) = cos (x):

(f или g) (x) = f (g (x)) = cos 3 (Икс)

Его производная и его неопределенный интеграл:

Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Построить график ЛИНЕЙНОЙ функции и найти:

Пример 2

Найдите композицию функции g с функцией f, где g и f — функции, определенные в предыдущем примере:

(g или f) (x) = g (f (x)) = cos (x 3 )

Следует отметить, что композиция функций не является коммутативной операцией.

Производная и неопределенный интеграл для этой функции соответственно равны:

Интеграл оставлен указанным, потому что невозможно точно записать результат в виде комбинации элементарных функций.

Видео:Сложная функция. Алгебра 10Скачать

Сложная функция. Алгебра 10

Ссылки

  1. Исчисление одной переменной. Рон Ларсон, Брюс Х. Эдвардс. Cengage Learning, 10 ноября 2008 г.
  2. Теорема о неявной функции: история, теория и приложения. Стивен Г. Кранц, Гарольд Р. Паркс. Springer Science & Business Media, 9 ноября. 2012 г.
  3. Многопараметрический анализ. Сатиш Ширали, Харкришан Лал Васудева. Springer Science & Business Media, 13 декабря. 2010 г.
  4. Системная динамика: моделирование, моделирование и управление мехатронными системами. Дин К. Карнопп, Дональд Л. Марголис, Рональд К. Розенберг. John Wiley & Sons, 7 марта 2012 г.
  5. Исчисление: математика и моделирование. Уильям Баулдри, Джозеф Р. Фидлер, Фрэнк Р. Джордано, Эд Лоди, Рик Витрей. Эддисон Уэсли Лонгман, 1 января 1999 г.
  6. википедия. Трансцендентная функция. Получено с: es.wikipedia.com

Когнитивная карта: виды, характеристики и примеры

Вестибулокохлеарный нерв: что это такое и какие функции выполняет

Видео:10 класс, 10 урок, Обратная функцияСкачать

10 класс, 10 урок, Обратная функция

63. Основные трансцендентные функции

Определение. Трансцендентными называются аналитические функции, которые не являются алгебраическими.

Если аргументом показательной или тригонометрических функций является комплексное число, то определение этих функций, вводимое в элементарной алгебре теряет смысл.

Рассмотрим разложение в степенной ряд следующих функций:

В трансцендентном уравнении функции f и g является аналитические функции

В трансцендентном уравнении функции f и g является аналитические функции

В трансцендентном уравнении функции f и g является аналитические функции

См. Представление функций по формуле Тейлора.

Функции ez, cosz, sinz связаны между собой формулой Эйлера (см. Уравнение Эйлера.) Эта формула может быть очень легко получена сложением соотвествующих рядов.

В трансцендентном уравнении функции f и g является аналитические функции

Также справедливы равенства:

В трансцендентном уравнении функции f и g является аналитические функции

В трансцендентном уравнении функции f и g является аналитические функции

В трансцендентном уравнении функции f и g является аналитические функцииВ трансцендентном уравнении функции f и g является аналитические функции

В трансцендентном уравнении функции f и g является аналитические функции

Для тригонометрических функций комплексного аргумента справедливы основные тригонометрические тождества (синус и косинус суммы, разности и т. д.), которые справедливы для функций действительного аргумента.

Определение. Гиперболическим синусом, косинусом, тангенсом и котангенсом Называются соответственно функции:

В трансцендентном уравнении функции f и g является аналитические функции

Гиперболические функции могут быть выражены через тригонометрические:

В трансцендентном уравнении функции f и g является аналитические функции

Гиперболические функции Sh Z И Ch Z имеют период 2pi, а функции Th Z и Cth Z – период pi.

Пример. Найти sin(1+2i).

В трансцендентном уравнении функции f и g является аналитические функции

В трансцендентном уравнении функции f и g является аналитические функции

Определение. Логарифмическая функция комплексного аргумента определяется как функция, обратная показательной.

В трансцендентном уравнении функции f и g является аналитические функции

Если W = U + Iv, то В трансцендентном уравнении функции f и g является аналитические функциии Arg Ew =В трансцендентном уравнении функции f и g является аналитические функции = V.

Тогда Eu = В трансцендентном уравнении функции f и g является аналитические функции.

Итого: В трансцендентном уравнении функции f и g является аналитические функции

Для комплексного числа Z = A + Ib В трансцендентном уравнении функции f и g является аналитические функции

Определение. Выражение В трансцендентном уравнении функции f и g является аналитические функцииназывается Главным значением логарифма.

Логарифмическая функция комплексного аргумента обладает следующими свойствами:

1) В трансцендентном уравнении функции f и g является аналитические функции

2) В трансцендентном уравнении функции f и g является аналитические функции

3) В трансцендентном уравнении функции f и g является аналитические функции

4) В трансцендентном уравнении функции f и g является аналитические функции

Обратные тригонометрические функции комплексного переменного имеют вид:

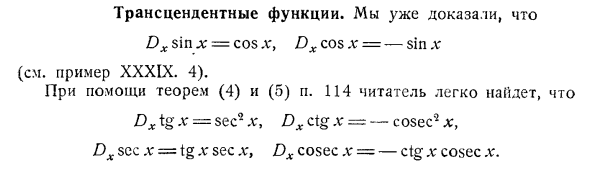
Видео:СПОРИМ ты поймешь Математику — Функция и ее свойства, Область определения, Нули ФункцииСкачать

СПОРИМ ты поймешь Математику — Функция и ее свойства, Область определения, Нули Функции

Трансцендентная функция — аналитическая функция, не являющаяся алгебраической

В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции

В трансцендентном уравнении функции f и g является аналитические функции

Видео:Отображения множествСкачать

Отображения множеств

Трансцендентные функции

Трансцендентальная функция. Мы уже доказали это Dx sin l: = cos x, Dx cos x = -sin x (Пример XXXIX, см. 4). Используя теорему (4) и (o) в стихе 114, читатели могут легко найти ее. Dx t g .v = sec2 L ‘, Dx ctg x = -cos it * x, Dx sec x = tg x sec x, Dx cosec x = -ig x cosec x

Теорема (7) позволяет легко найти производную обратной функции циркуляции. Читатель должен проверить следующую формулу: Dx arc sin x = zh. , Dx arc cos l: = 1 ^ arctgArrrry ^, Z) ^ arcctgA: = —j-p ^, D .arc sec * = ± — / * ■ -, Dx arc cosec x X Y ^ X * -1 * * dgu ^ -Г

Это легко вывести из теоремы (6) и (7) в разделе 114. Людмила Фирмаль

Видео:Математика для всех. Алексей Савватеев. Лекция 6.9. Алгебраические и трансцендентные числаСкачать

Математика для всех. Алексей Савватеев. Лекция 6.9. Алгебраические и трансцендентные числа

Примеры решения, формулы и задачи

Решение задачЛекции
Расчёт найти определенияУчебник методические указания
  • Для функций arc sin x и arc cosec x берется знак, соответствующий знаку cos (arc sin x), а для arc cos x и arc sec l * знак совпадает со знаком sin (arc cos x) Я сделаю это Следующее более общее выражение также очень важно: Z ^ arc sin — ===: £ _! =, Dx arctg — == L а х а х * — — а **

В первом разделе знак cos (arc sin так Ci как В зависимости от того, положительный он или отрицательный. Наконец, теорема §114 (6) может использоваться для различения комплексных функций, которые состоят как из алгебраических, так и из тригонометрических функций.

Следовательно, вы можете вычислить производную функции, как показано в следующем примере. Людмила Фирмаль

В трансцендентном уравнении функции f и g является аналитические функции

В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции В трансцендентном уравнении функции f и g является аналитические функции

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

🎬 Видео

Логарифмическая функция, ее свойства и график. 11 класс.Скачать

Логарифмическая функция, ее свойства и график. 11 класс.

Математика это не ИсламСкачать

Математика это не Ислам

10 класс, 20 урок, Функции y=tgx, y=ctgx, их свойства и графикиСкачать

10 класс, 20 урок, Функции y=tgx, y=ctgx, их свойства и графики
Поделиться или сохранить к себе: