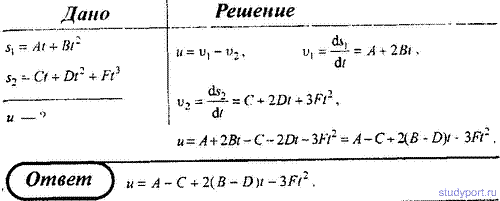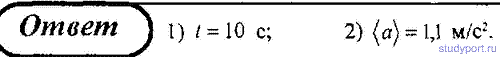В течении времени t скорость тела задается уравнением u a bt ct 2 (2 видео)

В течении времени t скорость тела задается уравнением u a bt ct 2

В течение времени τ скорость тела задается уравнением вида v = А + Bt + Ct 2 (0 ≤ t ≤ τ). Определите среднюю скорость за промежуток времени τ.

Скорость реактивного самолета на некотором участке меняется с расстоянием по закону v = D + Bs. Найти работу за промежуток времени (t₁,t₂), если масса самолета m. В момент времени t₁ скорость равна v₁.

Циклическая частота свободных незатухающих колебаний материальной точки ω₀. Определить наименьший промежуток времени, за который потенциальная энергия колебаний уменьшается в два раза по сравнению со своим наибольшим значением.

Сила F = 20 Н, действовавшая в течение короткого промежутка времени t = 10 –2 c на покоящееся тело, сообщила ему кинетическую энергию 3 Дж. Какую энергию сообщит эта сила тому же телу за то же время, если начальная скорость тела 10 м/с, а сила действует в направлении скорости?

На материальную точку М действует сила F = 3t 2 i + 4tj. Определить проекцию импульса силы на ось Ох за промежуток времени τ = t₂ – t₁, где t₂ = 2 с, t₁ = 0.

Электрон в бетатроне движется по орбите радиусом r = 0,4 м и приобретает за один оборот кинетическую энергию T = 20 эВ. Вычислить скорость изменения магнитной индукции d /dt, считая эту скорость в течение интересующего нас промежутка времени постоянной.

Закон движения материальной точки имеет вид: X(t) = (3–t) 2 . Найти перемещение и пройденный путь за промежуток времени от t₁ = 2 c до t₂ = 4 c, а также среднюю путевую скорость и среднюю скорость перемещения.

Закон движения материальной точки имеет вид: X(t) = A+Bt+Ct 2 , где A = 25 м, B = 10 м/с, C = 1 м/с 2 . Найти перемещение, пройденный путь, среднюю путевую скорость и среднюю скорость перемещения для промежутка времени от t₁ = 2 с до t₂ = 6 c.

Маховик начал вращаться равноускоренно и за промежуток времени t = 10 с достиг частоты n = 300 мин –1 . Запишите уравнение зависимости φ = f(t) рад, согласно которому вращается диск.

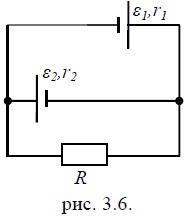
Два источника ЭДС ε₁ = 10 В, ε₂ = 8 В с внутренними сопротивлениями r₁ = 1,0 Ом и r₂ = 2,0 Ом включены параллельно реостату R = 6,0 Ом (рис.3.6). Определите: 1) силу тока в источниках и реостате; 2) работу, совершенную источниками за промежуток времени Δt = 10,0 с.

Определите величины токов во всех участках цепи (рис. 16.15), если ε₁ = 24 В, ε₂ = 18 В, r₁ = 0,2 Ом, r₂ = 0,5 Ом, R₁ = 20 Ом, R₂ = R₃ = 2,0 Ом. Чему равна работа, совершенная источниками за промежуток времени Δt = 0,1 с?

Зная постоянную распада λ ядра, определить: а) вероятность того, что оно распадется за промежуток времени от 0 до t; б) его среднее время жизни τ.

На частицу массой m действует сила F = α ехр (–βt), где α и β — положительные постоянные. При t = 0 скорость частицы v = 0. Найти работу силы за очень большой промежуток времени (t → ∞).

В течение времени τ скорость тела задается уравнением V = A + Bt + Ct 2 (0

Содержание

Кинематика
Контрольная работа по физике 1
Примеры решения задач по классической и релятивистской механике
💥 Видео

Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Кинематика

1. Физические основы механики

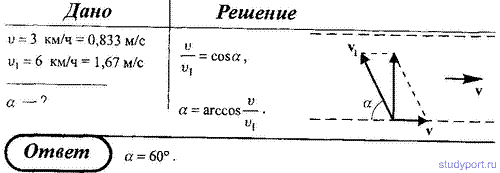
1. Скорость течения реки v, а скорость движения лодки относительно воды v₁. Определить, под каким углом относительно берега должна двигаться лодка, чтобы проплыть поперек реки.

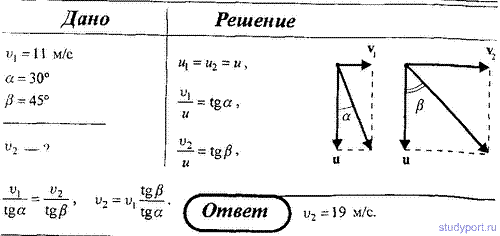
2. Капля дождя при скорости ветра v₁ падает под углом α к вертикали. Определить, при какой скорости ветра v₂ капля будет падать под углом В.

3. Два автомобиля, выехав одновременно из одного пункта, движутся прямолинейно в одном направлении. Зависимость пройденного ими пути задается уравнениями s₁ = At + Bt 2 и s₂ = Ct + Dt 2 + Ft 3 . Определить относительную скорость u автомобилей.

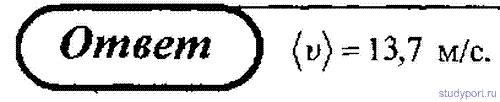
4. Велосипедист проехал первую половину времени своего движения со скоростью v₁, вторую половину времени – со скоростью v₂. Определить среднюю скорость движения велосипедиста.

5. Велосипедист проехал половину пути со скоростью v₁ = 16 км/ч, вторую половину пути — со скоростью v₂ = 12 кмч. Определите среднюю скорость движения велосипедиста.

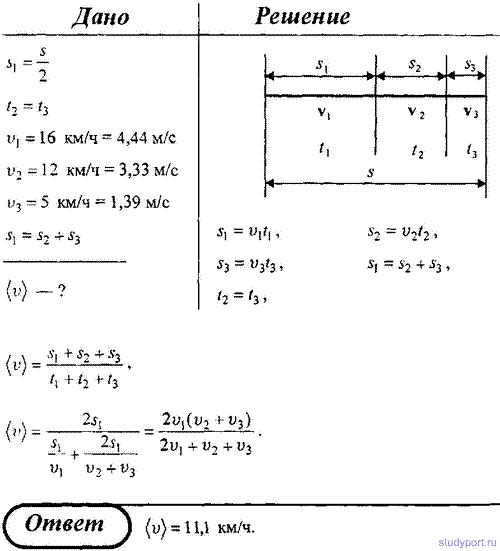
6. Студент проехал половину пути на велосипеде со скоростью v₁ = 16 Далее в течение половины оставшегося времени он ехал со скоростью v₂ = 12, а затем до конца пути шел пешком со скоростью v₃ = 5. Определить среднюю скорость движения студента на всем пути.

7. В течении времени τ скорость тела задается уравнением вида v = A + Bt + Ct 2 (0 2 + Dt 3 (A = 6 м, B = 3 м/с, C = 2 м/с 2 , D = 1 м/с 3 ) Определить для тела в интервале от t₁ = 1 до t₂ = 4 с: 1) среднюю скорость; 2) среднее ускорение.

19. Зависимость пройденного телом пути от времени задается уравнением s(t) = A + Bt + Ct 2 + Dt 3 (C = 0,1 м/с 2 , D = 0,03 м/с^ 3 ) Определите: 1) через сколько времени после начала движения ускорение тела будет равно 2 м/с 2 ; 2) среднее ускорение (a) тела за этот промежуток времени.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Видео:Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

Контрольная работа по физике 1

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Примеры решения задач по классической и релятивистской механике

1. В течение времени τ скорость тела задается уравнением вида A+Bt+Ct²
(0 ≤ t ≤ τ). Определить среднюю скорость за промежуток времени τ.

Средняя скорость тела за время τ:

Ответ: = A+Bτ/2+Cτ 2 /3.

2. Мяч, брошенный со скоростью 10 м/с под углом 45 0 к горизонту, ударяется о стенку, находящуюся на расстоянии 3 м от места бросания. Когда происходит удар мяча о стенку (при подъеме мяча или при его опускании)? На какой высоте мяч ударится о стенку (считая от высоты, с которой брошен мяч)? Найти скорость мяча в момент удара.

Горизонтальная составляющая скорости не изменяется со временем и равна

С такой скоростью мяч пройдет путь l за время t₁:

По вертикали мяч начинает движение со скоростью

и движется равноускоренно. Вертикальная составляющая скорости изменяется по закону

В момент t₁ удара мяча о стену вертикальная составляющая скорости равна

Так как вертикальная составляющая скорости в момент удара мяча о стену положительна, то мяч ударился при подъеме.

В момент удара высота равна

Ответ: удар происходит при подъеме мяча; v₁ = 7,65 м/c; h = 2,12 м.

3. В вагоне, движущемся горизонтально с постоянным ускорением 3 м/с 2 , висит на проволоке груз массой 2 кг. Определить силу натяжения проволоки и угол ее отклонения от вертикали, если груз неподвижен относительно вагона.

На основании II закона Ньютона запишем

или в проекции на оси координат

Ответ: 1) Т = 20,51 Н; 2) φ = 17°.

4. На железнодорожной платформе, движущейся по инерции со скоростью 3 км/ч, укреплено орудие. Масса платформы с орудием 10 т. Ствол орудия направлен в сторону движения платформы. Снаряд массой 10 кг вылетает из ствола под углом 60 0 к горизонту. Определить скорость снаряда, если после выстрела скорость платформы уменьшилась в 2 раза.

v₀ = 3 км/ч = 0,833 м/с

М = 10 т = 10 4 кг

Вдоль оси x во время взаимодействия снаряда с платформой на систему не действуют внешние силы в горизонтальном направлении. Поэтому можно применить закон сохранения импульса для проекций импульсов системы на ось x.

Запишем закон сохранения момента импульса в проекции на ось x:

Ответ: v = 835 м/с.

5. Ветер действует на парус площадью S с силой F=ASρ(υ₀ -υ) 2 /2, где А – некоторая постоянная; ρ – плотность воздуха; υ₀ – скорость ветра, равная 15 м/с; υ − скорость лодки. Определить скорость лодки при максимальной мгновенной мощности ветра.

Мощность ветра ― это мощность, передаваемая ветром катеру:

где F ― сила ветра, действующая на парус;

v ― скорость лодки.

S ― площадь паруса;

ρ ― плотность воздуха;

v₀ ― скорость ветра.

Найдем экстремум функции N(v):

Решаем квадратное уравнение относительно v:

При v = v₀ мощность N = 0.

При v = v₀/3 = 5 м/с мощность

Ответ: v = v₀/3 = 5 м/с. N=250 ASp.

6. Полый тонкостенный цилиндр массой 0,5 кг, катящийся без скольжения, ударяется о стену и откатывается от нее. Скорость цилиндра до удара о стену равнялась 1,4 м/с, после удара 1 м/с. Определить количество теплоты, выделившееся при ударе.

В момент удара шара о стенку часть кинетической энергии шара перейдет в тепло Q. На основании закона сохранения энергии запишем

где ω₁ = v₁/R, ω₂ = v₂/R — угловые скорости шара до и после удара, J = mR 2 — момент инерции шара.

откуда найдем количество тепла

Ответ: Q = 0,48 Дж.

7. Период обращения кометы Галлея вокруг Солнца 76 лет. Минимальное расстояние, на котором она проходит от Солнца, составляет 180 Гм. Определить максимальное расстояние, на которое комета удаляется от Солнца. Радиус орбиты Земли принять равным 150 Гм.