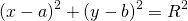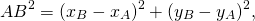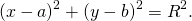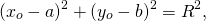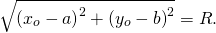В прямоугольной системе координат уравнение окружности радиусом r с центром в точке a x0 y0 (3 видео)

Уравнение окружности

Уравнение окружности с центром в точке (a;b) и радиусом R в прямоугольной системе координат имеет вид

1. Пусть в прямоугольной системе координат задана окружность с центром в точке A (a;b) и радиусом R (R>0).

Чтобы составить уравнение этой окружности, выберем на окружности произвольную точку B (x;y).

По определению окружности, расстояние от центра до любой точки окружности равно радиусу R, то есть AB=R.

Так как B (x;y) — произвольная точка окружности, координаты любой точки окружности удовлетворяют этому уравнению.

2. Если пара чисел (x_o;y_o) удовлетворяет данному уравнению, то

А это значит, что расстояние между точками C(x_o;y_o) и A(a;b) равно R. Значит, точка C(x_o;y_o) принадлежит окружности с центром в точке A(a;b) и радиусом R.

Следовательно, данное уравнение фигуры является уравнением окружности.

Содержание

Уравнение окружности, уравнение прямой
Уравнение окружности и прямой
Описание презентации по отдельным слайдам:
Математика: теория и методика преподавания в образовательной организации
Дистанционное обучение как современный формат преподавания
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
Материал подходит для УМК
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Автор материала
Дистанционные курсы для педагогов
Подарочные сертификаты
💥 Видео

Видео:Уравнение окружности (1)Скачать

Уравнение окружности, уравнение прямой

Уравнение окружности с радиусом R и с центром в точке O (( x_0;y_0)) имеет вид: (( x-x_0 )^2 + ( y-y_0)^2 = R^2 ) .

Если центр окружности совпадает с началом координат, то уравнение окружности упрощается: (x^2+y^2=R^2) .

Пример 1. Дано уравнение окружности: ((x-1)^2+(y+2)^2=4) . Найдем центр и радиус.

Решение: Центр этой окружности – точка (C(1;-2)) , радиус (R=2) .

Уравнение прямой на плоскости

Любую прямую на плоскости можно задать уравнением прямой первой степени вида (Ax + By + C = 0) , где A и B не могут быть одновременно равны нулю.

Уравнение прямой с угловым коэффициентом

Общее уравнение прямой при (b≠0) можно привести к виду:

(y = kx + b) , где (k) – угловой коэффициент, равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.

Уравнение прямой в отрезках на осях

Если прямая пересекает оси OX и OY в точках с координатами ((a; 0) и (0; b)) , то она может быть найдена, используя формулу уравнения прямой в отрезках: (frac+frac=1) .

Уравнение прямой, проходящей через две различные точки на плоскости

Если прямая проходит через две точки (A(x_1;y_1)) и (B(x_2; y_2)) , такие, что (x_1 ≠ x_2 и y_1 ≠ y_2) , то уравнение прямой можно найти, используя следующую формулу: (frac=frac) .

Пример 2. Составим общее уравнение прямой, которая в прямоугольной системе координат проходит через две точки (M_1(1;1)) и (M_2(4;2)) .

Решение: Сначала напишем уравнение прямой, проходящей через две заданные точки. Оно имеет вид (frac=frac Leftrightarrow frac3=frac1) . Теперь приведем полученное уравнение к требуемому виду: (frac3=frac1 Leftrightarrow 1cdot (x-1)=3cdot(y-1) Leftrightarrow x-3y+2=0) .

Составьте уравнение прямой, содержащей медиану (MK) треугольника (MDC) , если его вершины – (M(- 1; 5), D(8; — 2), C(- 4; — 2)) .

Найдите координаты точек пересечения окружности (x^2+y^2 — 8x- 8y + 7 = 0) с осью абсцисс.

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Уравнение окружности и прямой

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Описание презентации по отдельным слайдам:

ТЕМА: «Уравнение окружности и прямой» Цели урока: Повторить уравнение окружности и прямой. Показать применение уравнений окружности и прямой при решении задач. Совершенствование навыков решения задач методом координат.

1. Как называется геометрическая фигура, состоящая из множества всех точек, равноудаленных от данной точки? Математический диктант Проверить 1. Окружность

2. Как называется хорда, проходящая через центр окружности? Проверить 2. Диаметр

3. Как называется отрезок, соединяющий центр окружности с точкой на окружности? Проверить 3. Радиус

4. Как называется геометрическая фигура, состоящая из множества всех точек плоскости, находящихся от данной точки на расстоянии, не превышающем данного? Проверить 4. Круг

5. Пересекаются ли окружности с центрами А и В, если АВ = 10 см, а радиусы равны 5 см, и 6 см? Проверить 5. Пересекаются

6. Расстояние от центра окружности до точки А равно d, а радиус окружности равен r. Сравните d и r, если точка А лежит вне круга, ограниченного данной окружностью? Проверить 6. d > r

7. Расстояние от центра окружности до точки В равно m, а радиус окружности равен r. Сравните m и r, если точка B лежит внутри круга, ограниченного данной окружностью? Проверить 7. m (0 – 1)2 + (0 + 3)2 = 9 > (0 – 1)2 + (1 + 3)2 = 9 > x

Дана окружность Определите, какие из точек А(-4; 3), В(5; 1), С(-5; 4), D(10; 5) лежат: а) на окружности; б) внутри круга, ограниченного данной окружностью; в) вне круга, ограниченного данной окружностью. (x – 4 )2 + (y + 3)2 = 100 (– 4 – 4)2 + (3 + 3)2 > 100 (5 – 4)2 + (1 + 3)2 100 (10 – 4)2 + (5 + 3)2 = 100

Найдите множество точек, удаленных от окружности на расстояние 3. x 2 + y 2 = 16 x y x 2 + y 2 = 49 x 2 + y 2 = 1

(x + 5)2 + (y – 5)2 = 25 Центр? Радиус? O1(-5;5) r = 5 x y A O O1 450 5 5

Центр? Радиус? x y O1 O E 300 На чертеже расстояние ОО1= , ОЕ – касательная к окружности. EOF = 600. Написать уравнение окружности. ОЕ = ОF, отрезки касательных 6

Домашнее задание п. 93 — 95 № 972(б), 973, 978 (а)

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 693 человека из 75 регионов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 859 человек из 78 регионов

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

Сейчас обучается 49 человек из 21 региона

«Мотивация здорового образа жизни. Организация секций»

Свидетельство и скидка на обучение каждому участнику

Для всех учеников 1-11 классов
и дошкольников
Интересные задания
по 16 предметам

«Как закрыть гештальт: практики и упражнения»

Свидетельство и скидка на обучение каждому участнику

Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 842 302 материала в базе

Материал подходит для УМК

«Геометрия», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.

§ 3. Уравнения окружности и прямой

Ищем педагогов в команду «Инфоурок»

Другие материалы

09.11.2020
514
17

30.09.2020
395
11

09.01.2020
3798
195

21.12.2019
1508
45

30.11.2019
1240
47

31.10.2019
781
44

30.10.2019
2154
199

16.08.2019
846
9

«Учись, играя: эффективное обучение иностранным языкам дошкольников»

Свидетельство и скидка на обучение
каждому участнику

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

07.12.2020 1274
PPTX 3 мбайт
51 скачивание
Рейтинг: 5 из 5
Оцените материал:

Настоящий материал опубликован пользователем Малышок Елена Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

На сайте: 8 лет и 5 месяцев
Подписчики: 1
Всего просмотров: 36087
Всего материалов: 28

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:ДЕКАРТОВЫ КООРДИНАТЫ. Контрольная № 3 Геометрия 9 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минпросвещения рекомендует школьникам сдавать телефоны перед входом в школу

Время чтения: 1 минута

С 1 сентября в российских школах будут исполнять гимн России

Время чтения: 1 минута

Минпросвещения проведет Всероссийский конкурс для органов опеки и попечительства

Время чтения: 1 минута

В Госдуме предложили унифицировать школьные программы

Время чтения: 1 минута

Инфофорум о буллинге в школе: итоги и ключевые идеи

Время чтения: 6 минут

Российские школьники начнут изучать историю с первого класса

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.