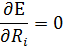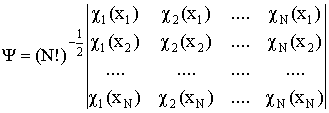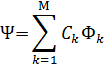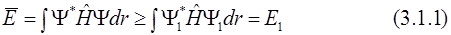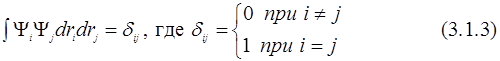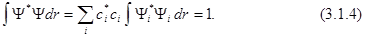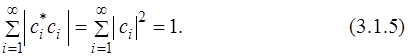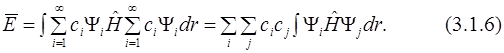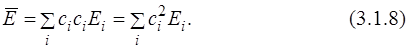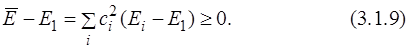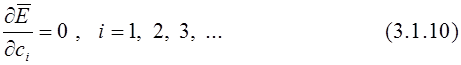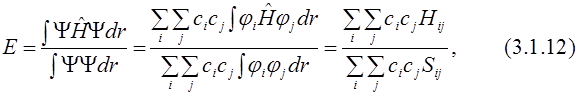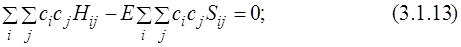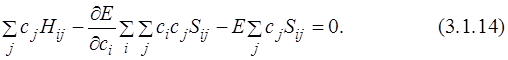Оба эти приближения основаны на том, что масса ядер примерно в тысячи раз больше массы электрона. Электроны движутся с высокой скоростью около 1% от скорости света. Поэтому можно считать, что электрон движется в поле покоящихся ядер. В этом заключается смысл приближений. ( формулы лекций). Допустим, известно решение электронного уравнения Шредингера.
параметры задаются до начала решения уравнения. Поскольку оператор Гамильтона эрмитов, то мы выбираем решение электронного уравнения Шредингера ввиде ортонормированных электронноволновых функций.
(формулки тут всякие) для того, чтобы упростить полученные уравнения мы используем свойство ортонормальности электроноволновых функций.
Переходим к интегралам умножая слева на житую электронную функцию и интегрируем…( еще куча формулок) Приближение Борна-Оппенгеймера заключается в приближении элементами не адиабатического приближения 1,2 порядка. (формулки) Не адиабатические элементы ответственны за преобразование типа электронноволновой функции при изменении ядерных координат. Адиабатическое приближение и приближение Оппенгеймера не применимо в том случае, если при изменении ядерной конфигурации меняется тип конфигурации. Ядерные параметры становятся переменными. В адиабатическом приближении остается 1 не адиабатический элемент 2 порядка для i=j. Этот вклад называется диогональной коллекцией (формулка). Чаще всего приближение Борна – Оппенгеймера не применимо к фотохимическим реакциям и иногда не применимо к реакциям сопровождающимся гомолитическими разрывами связи. (реакция)
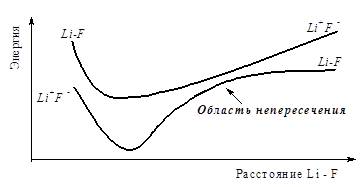
молекула LiF полярна и описывается ввиде 2 суперпозиций 2-х волновых функций полярной и неполярной. Энергия полярной меньше энергии неполярной, но полярная молекула диссоциирует на атомы.
Изолированные атомы устойчивее ионов. Для разделенных Li и F энергия ионноволновой функции больше чем энергия неполярной волновой функции.
Р и с. 3.2. Кривые диссоциации молекулы Li-F
В области пересечения приближения Оппенгеймера неприменимо. После принятия приближения Борна – Оппенгеймера молекулярное уравнение Шредингера распадается на 2 уравнения ( формулки) .
Сначало решают электронное уравнение Шредингера при заданных координатах ядер. Координаты ядер можно задать 2 способами. Далее оптимизируют геометрию с целью поиска минимума эл. Энергии.
Далее решают ядерное уравнение Шредингера. Из найденной ядерно-волновой функции вычисляются колебательные и вращательные уровни Е.
Эти результаты помогают вычислить ИК спектры, микроволновые спектры, комбинационно рассеянные (Романовские).
Решение ядерного уравнения позволяет вычислить энергию нулевых колебаний ядер, а также энергию колебательную, поступательную и вращательную движения молекулы в целом. Эти 4 вклада необходимы для вычисления энергетического характера молекул при стандартных условиях.
Классификация движений молекул позволяет вычислить как энтропию, так и энтальпию энергетических молекул. Зная энтропию, можно узнать энегрия Гиббса. Е эл. (типа стрелочка вправо) ΔЕ, G°( тоже стрелка) ΔG°.
ΔЕ практически ΔG°
Орбитальная модель. Электронный оператор Гамильтона. Одноэлектронный гамильтониан и оператор электронного отталкивания. Понятия «орбиталь», «спин-орбиталь». Спин-орбитальный детерминант (детерминант Слэйтера). Полная формулировка орбитальной модели.
Орбитальная модель – графическое изображение распределения плотности заряда электрона в атоме… Обоснование орбитальной модели атома, исходящее из корпускулярного характера электрона, состоит в следующем. Вероятность определенного положения электрона внутри объема пространства, окружающего атомное ядро, весьма велика, так как рассматривается устойчивое ( реально существующее) состояние атома. Такое распределение следует понимать так, что на любом выбранном расстоянии от ядра вероятность пребывания электрона одинакова во всех направлениях радиуса-вектора. Как следует из рис. 9, вероятность пребывания электрона в атомном ядре равна нулю, она незначительна вблизи ядра, но быстро возрастает при удалении от ядра. На некотором расстоянии ( для атома водорода оно равно. Бора) вероятность достигает максимума, а затем, медленно уменьшается, асимптотически приближаясь к нулю на расстоянии, стремящемся к бесконечности
Электронный оператор Гамильтона— (Оператор набла ∇ )– это символический вектор, сочетающий в себе векторные и дифференцирующие свойства.
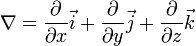
Более близкие к истинным решения получают с помощью метода самосогласованного поля (ССП), предложенного Хартри. В методе ССП межэлектронным отталкиванием не пренебрегают, но действие на данный электрон всех остальных электронов заменяют средним полем, приближенно воспроизводящим их суммарное действие; последнее зависит от координат только рассматриваемого электрона. Это дает возможность разделить в сферической системе координат переменные в уравнении Шредингера. С формальной точки зрения это достигается следующим образом. Одноэлектронный гамильтониан записывают в виде: http://quant.distant.ru/files/Atom/Atom_razd.pdf (со стр 8 формулы)
Последнее слагаемое описывает отталкивание между электронами i и j, усредненное по всем положениям электрона j и, следовательно, зависящее только от координат электрона i . Последствия этого состоят в следующем.
Рассмотрим гамильтониан ( формула)
Его собственные функции (функции Хартри) имеют вид орбитальных произведений: ( формула)
Собственные значения Н представляются суммой собственных значений h i ССП : ( опять долбанная формула)
Энергия εi есть сумма кинетической энергии i-го электрона, потенциальной энергии его притяжения к ядру и средней потенциальной энергии его отталкивания от остальных электронов. Следовательно, Е` есть сумма кинетической энергии всех электронов, потенциальной энергии их притяжения к ядру и удвоенной потенциальной энергии их усредненного отталкивания от остальных электронов. Удвоение возникло потому, что отталкивание между электронами i и j учтено дважды: как среднее по j в hi ССП и среднее по i в hj ССП . С учетом этого, полная энергия атома равна: ( формулы) Соответственно, гамильтониан атома должен иметь вид: (формулы) Таким образом, необходимо решить систему одноэлектронных уравнений с гамильтонианом (45), включающим усредненное межэлектронное взаимодействие – систему уравнений Хартри. Для этого нужно построить набор операторов hi ССП для чего следует прежде рассчитать усредненные величины (формул). Значит, отталкивание электрона i, усредненное по всем положениям электрона j, равно: (формула)
Однако, чтобы вычислить этот интеграл, волновые функции χ j (rj) должны уже быть известны! Это противоречие преодолевается следующим образом. Сначала задаются некоторым набором N одноэлектронных функций, максимально близких к правильным χ j 0 (rj) (позже мы увидим, что сделать это легко). С их помощью вычисляют интеграл (46) и строят оператор (hi 0 ) ССП . Затем решают набор одноэлектронных уравнений Хартри, возникающий из условия минимума среднего значения гамильтониана (40), вычисляемого с волновой функцией Хартри (42): ( формула)
Полученные решения χ j 1 (rj) используют, чтобы построить «исправленный» оператор (hi 1 ) ССП , вновь решают ту же систему уравнений, но теперь – с (hi 1 ) ССП и т.д. – до тех пор, пока получаемые собственные значения уравнений Хартри (т.е. энергии состояний) будут отличаться от полученных на предыдущей итерации лишь на очень незначительную величину (
10 -6 а.е.) Этот процесс называется самосогласованием, а результирующее поле, создающее усредненный потенциал в (40), называется самосогласованным полем – отсюда и название метода. ( хз то ли вообще, другого не нашла)
ОРБИТАЛЬ – область наиболее вероятного местонахождения электрона в атоме (атомная орбиталь) или в молекуле (молекулярная орбиталь).
Спин-орбиталь — это одноэлектронная волновая функция, получаемая из орбитали умножением ее на «спин-функцию», описывающую спиновое состояние отдельного электрона.
Детерминант Слейтера – детерминант, построенный из ортонормированных спин-орбиталей — атомных или молекулярных. Позволяет получить приближенную многоэлектронную волновую функцию N электронов, обеспечивая ее правильные антисимметричные свойства. Элементы детерминанта Слейтера есть описывающие электроны орбитали и перестановка электронов эквивалентна перестановке местами столбцов (строк) детерминанта, что изменяет его знак:
Детерминант Слейтера является единственной функцией, обеспечивающей антисимметричность волновой функции, записанной через орбитали (орбитальное приближение). Следовательно, он дает только одно решение соответствующих одноэлектронных уравнений. Хотя электроны неразличимы, в орбитальном приближении каждый электрон описывается «своей» волновой функцией. Системы, в которых все электроны занимают орбитали попарно, называются системами с закрытыми (замкнутыми) электронными оболочками. Для таких систем детерминант Слейтера состоит из дважды занятых электронами орбиталей, число которых равно половине числа электронов. Системы с нечетным числом электронов называются системами с открытыми (незамкнутыми) оболочками.
Наиболее полная формулировка орбитальной модели такова:
волновая функция многоэлектронной системы может быть представлена ввиде линейной комбинации функций Фk ( k=1,2,…М)
Каждая функция Фk особым образом построена из множества (набора) спин-орбиталей ψ(r, ϭ). Каждая из спин-орбиталей представляет из себя произведение : ψ(r, ϭ)=φ(r) * η(ϭ).
Одной из орбиталей φ(r), входящих в исходный набор ортонормированных функций φi(r), i=1,2…,К., и одной из двух ортонормированных спиновых функций ηi(ϭ), i=1,2.
Применение вариационного принципа для оптимизации волновой функции орбитальной модели. Линейный вариационный метод (метод Ритца). Вековое (секулярное) уравнение. Гамильтонова матрица.
Решением дифференциального уравнения Шрёдингера является волновая функция, и для ее поиска используется вариационный принцип, основанный на следующей теореме:
Пусть самое низкое собственное значение оператора Гамильтона для исследуемой системы равно Е1, а Ψ1 – точная волновая функция, соответствующая этому собственному значению. То есть точная функция Ψ1 определяет основное состояние системы с энергией Е1. В этом случае для любой произвольной нормированной функции Ψ выполняется условие:
(условимся, что r – набор координат всех рассматриваемых частиц, а знак интеграла – многомерный интеграл с пределами интегрирования по всему пространству: от 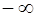
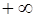
Согласно вариационному принципу, энергия любой пробной функции будет не меньше энергии точной функции. Действительно, произвольная функция Ψ может быть представлена в виде разложения в ряд по собственным функциям оператора Гамильтона:
Будем считать эти функции ортонормированными (здесь δij – символ Кронекера):
Если функция Ψ нормирована, то
Отсюда следует, что
Подставим разложение неизвестной функции по собственным функциям (3.1.2) в уравнение для средней энергии (см. постулат 5) (будем считать для простоты все функции и коэффициенты ci действительными):
Здесь интеграл отличен от 0 только при равных i и j, т.к. функции ортогональны (3.1.3). С учётом того, что
Теперь надо показать, что разность между средней энергией ( 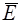
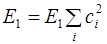
Действительно, выражение под знаком суммы всегда положительно или равно нулю, т.к. 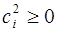
Приближённая функция Ψ называется пробной волновой функцией. Чем лучше пробная функция аппроксимирует точную, тем ближе вычисленное значение энергии к точному. При этом вычисленное значение всегда будет не меньше точного.
Коэффициенты 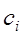
Однако в действительности полный набор собственных функций оператора Гамильтона неизвестен. Найти полный набор невозможно хотя бы потому, что он бесконечен. Поэтому Ритц предложил использовать пробную волновую функцию в виде линейной комбинации некоторых независимых функций. При этом число этих функций конечно и равно n, а сами функции не являются ортонормированными:
где 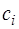
где Hij и Sij – матричные элементы оператора Гамильтона и матрицы перекрывания соответственно ( 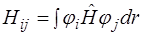
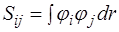
Перепишем уравнение в другом виде и продифференцируем его по коэффициентам 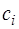
Так как 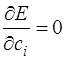
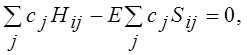
Полученная система однородных линейных уравнений имеет нетривиальное решение только тогда, когда её детерминант равен нулю:
Уравнения (3.1.16) называются секулярными, или вековыми. При решении системы уравнений (3.1.16) находят корни Е1, Е2, …, En. Наименьший корень соответствует энергии основного состояния, остальные – энергиям возбуждённых состояний. Для нахождения функции основного состояния необходимо подставить в систему уравнений найденное значение Е1 и найти коэффициенты 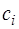
Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

ПРИБЛИЖЕНИЕ БОРНА-ОППЕНГЕЙМЕРА
Квантовая механика позволяет описать электронное строение и спектры атомов. Она также дает ответы на основные вопросы теории химического строения, которые были рассмотрены ранее:
- 1) почему атомы отдельных элементов соединяются в молекулу, т. е. почему устойчивы одни молекулы и неустойчивы другие;
- 2) в каком порядке могут объединяться атомы, т. е. каково химическое и пространственное строение молекул, каковы свойства химических связей.
Оператор Гамильтона молекулы с N ядрами и п электронами содержит члены кинетической энергии электронов, потенциальной энергии притяжения электронов к ядрам, а также члены, обусловливающие межэлектронное отталкивание. Кроме того, по сравнению с гамильтонианом атома добавляется член электростатического отталкивания ядер и их кинетической энергии:
где индексы аир принадлежат атомным ядрам, а индексы ; и ] относятся к электронам; Да() = |КЦ — Нр|, Д,„ = |г,- — 11а|
Так как гамильтониан молекулы (4.15) зависит не только от координат электронов, но и от ядерных координат, полная волновая функция системы должна содержать как электронные (г), так и ядерные (Д) координаты волновой функции |/(г, Д). Это значительно усложняет задачу математического поиска волновой функции. Поэтому в конкретных расчетах молекулярных свойств стремятся обычно к раздельному рассмотрению движения ядер и электронов.
Вид гамильтониана (4.15) существенно усложнен по сравнению с гамильтонианом многоэлектронного атома (3.2) главным образом из-за наличия члена кинетической энергии ядер. Однако масса ядра значительно превышает массу электрона, даже масса легчайшего ядра водорода (протона) в 1836 раз больше массы электрона. Соответственно скорость движения ядер значительно меньше по сравнению со скоростью движения электронов. В результате медленно движущиеся ядра образуют электростатическое поле, в котором с намного большей скоростью движутся электроны, успевающие почти мгновенно подстроиться к любому изменению координат ядер. Поэтому в первом приближении можно считать ядра атомов фиксированными и рассматривать только движение электронов. В рамках квантовой механики такое приближение эквивалентно допущению, что полная волновая функция молекулы |/(г, Д) может быть выражена в виде произведения электронной |/э(г, Д) и ядерной уя(Д) функций:
Координаты ядер К входят в |/э(г, К) в качестве параметров, а не переменных величин.
Рассмотрим условия, при которых справедливо допущение (4.16). Запишем уравнение Шрёдингера для молекулы с гамильтонианом (4.15) и волновой функцией (4.16):
где
— энергия отталкивания ядер;
— энергия притяжения электронов к ядрам;
— энергия отталкивания электронов.
Введем следующие обозначения операторов:
Электронная функция уэ(г, И) определяется как собственная функция оператора Нэ:
где Еэ — суммарная энергия, включающая электронную энергию К. обусловленную движением п электронов в поле N ядер молекулы, и энергию взаимодействия между ядрами Уяя (эту величину называют адиабатическим электронным термом молекулы или адиабатическим потенциалом).
Таким образом, полный гамильтониан молекулы состоит из суммы членов, соответствующих кинетической энергии (Т) и потенциальной энергии (10. которые можно записать следующим образом:
где индексы «э» и «я» относятся, соответственно, к электронам и ядрам.
Следует отметить, что в уравнении (4.21) не учтены некоторые малые члены, зависящие от спинов электронов и ядер. В соответствии с уравнением (2.11) операторы кинетической энергии являются дифференциальными, а члены, соответствующие потенциальной энергии, имеют тот же вид, что и в классической механике. Так, оператор отталкивания между электронами Уэа в атомных единицах имеет вид
где г,у — расстояние между электронами г и у.
Если из выражения (4.21) убрать член, соответствующий кинетической энергии ядер, то оставшаяся часть будет представлять собой гамильтониан для неподвижных ядер, который называют электронным гамильтонианом На:
Оператор Нэ зависит от положений как электронов, так и ядер, потому что от них зависит Уая, но для любой конкретной конфигурации ядер Нэ содержит в качестве переменных лишь координаты электронов. Решения уравнения Шрёдингера
определяют электронные волновые функции у? и электронные энергии Е?, характерные для рассматриваемой ядер- ной конфигурации. Энергия Е? в уравнении (4.24) называется потенциальной энергией, в которой движутся ядра.
Условие (4.16) означает, что электронная волновая функция уэ должна быть настолько медленно меняющейся функцией ядерных координат Л, что можно пренебречь ее первой и второй производными по этим координатам. М. Борн и Р. Оппенгеймер (1927) впервые показали, что электронные волновые функции обычно подчиняются этому условию с требуемой степенью точности. Такое приближение является весьма существенным для квантовой химии, его называют приближением Борна-Оппенгеймера или простым адиабатическим приближением. В нем полная энергия молекулы представляет собой сумму электронной энергии, вычисленной при фиксированной конфигурации ядер, и колебательно-вращательной энергии ядер:
Естественно, возникает вопрос, насколько оправданно использование приближения Борна-Оппенгеймера в квантовохимических расчетах и каковы при этом ошибки. Рассмотрим этот вопрос более подробно.
Как уже было отмечено, основой приближения Борна- Оппенгеймера является предположение о том, что относительное положение атомных ядер медленно меняется по сравнению с положением электронов (адиабатическое приближение). Положение атомного ядра и его колебания относительно точки равновесия можно сравнительно легко определить по отклонению рентгеновских лучей или другими методами. Это приближение позволяет, следовательно, задавать структуру расположения ядер и в соответствии с ней вычислять состояния электронов.
Для случая устойчивых многоатомных молекул существует простой критерий применимости адиабатического приближения:
где V — наибольшая из частот малых колебаний ядер вблизи точки равновесия, Е% и Е%, — энергии двух соседних электронных состояний.
Критерий (4.26) обычно выполняется для многих молекул, вследствие этого расчеты различных физических характеристик молекул, основанные на простом адиабатическом приближении (приближении Борна-Оппенгеймера), позволяют получить результаты, хорошо согласующиеся с экспериментальными данными. Причем адиабатическая поправка уменьшается с ростом массы ядер. Даже для самых легких молекул эта поправка очень мала: для Н2 она равна 0,016%, а для Б2 — 0,007%. Естественно ожидать, что для молекул, содержащих более тяжелые ядра, приближение Борна-Оппенгеймера будет выполняться с достаточной для квантовохимических расчетов точностью.
Видео:Лекции 5-6. Уравнение Шредингера и его приближенные решения. Межатомные.Скачать

Разделение электронного и ядерного движений
Для раздельного рассмотрения движения ядер и электронов учитывают, что масса ядра значительно превышает массу электрона (например, масса легчайшего ядра — протона
в 1836 раз больше массы электрона). Борн и Оппенгеймер показали, что величины электронной, колебательной и вращательной энергий двухатомной молекулы с приведенной массой |! находятся в следующем соотношении:
Для молекулы водорода это дает соответственно
В квантовой химии большое значение для проверки качества осуществленных квантово-механических расчетов имеет теорема вириала. Она устанавливает соотношения между полной, кинетической Т и потенциальной U энергиями, которые должны выполняться при точных решениях для любых квантово-механических систем. Так, при равновесной геометрии справедливы соотношения
Поэтому в вышеприведенном соотношении находятся и кинетические энергии различных форм движения, а это значит, что скорость движения ядер мала по сравнению со скоростью движения электрона. В результате движение электронов можно рассматривать независимо от медленного движения ядер.
Поскольку гамильтониан взаимодействия электронов с ядрами нельзя разделить на составляющие, зависящие только от координат электронов и только от координат ядер, ищут частное решение, получающееся при фиксированных положениях ядер. В этом случае полная волновая функция молекулы ЧДг, R) может быть выражена в виде произведения электронной v|/(r, R) и ядерной f„(R) функций:
Причем координаты ядер R входят в 1|/(г, R) в качестве параметров.
Поскольку некоторые квантово-механические операторы (импульса, кинетической энергии) содержат первую или вторую производные волновой функции по координатам, то предположение о разделении ядерного и электронного движения (8.4) справедливо тогда, когда этими производными по ядерным координатам можно пренебречь. Борн и Оппенгеймер показали, что электронные волновые функции обычно меняются в зависимости от ядерных координат достаточно медленно и можно пренебречь ее упомянутыми производными по ядерным координатам. Такое пренебрежение позволяет гамильтониан (8.3) заменить приближенным выражением, называемым электронным гамильтонианом
Тогда электронное уравнение Шрёдингера можно решить при фиксированных («замороженных» R0) координатах ядер и не учитывать движения ядер
Используемые при этом допущения называются грубым приближением Борна — Оппенгеймера.
Для описания движения ядер требуется решить соответствующее ядерное уравнение с ядерным гамильтонианом
Однако для этого нужно знать потенциал E(Ra,Rh. RN ), создаваемый для ядер всеми электронами, т.е. иметь решения электронного уравнения при всех положениях ядер. Величина E(Ra,Rb. RN ) определяется набором собственных значений гамильтониана при различных координатах ядер. Обычно она вычисляется в координатах, характеризующих относительное расположение ядер. Она является многомерной потенциальной функцией и выше была определена как поверхность потенциальной энергии. Ее также называют термом (энергетическим уровнем) молекулы. Такой учет движения ядер называется приближением Борна — Оппенгеймера.
Электронный гамильтониан можно дополнить поправкой первого порядка по теории возмущений, если в качестве возмущения выбрать отсутствующий в нем оператор кинетической энергии ядер
Возникающее при этом более точное приближение называется адиабатическим приближением (первого порядка).
Разделение электронного и ядерпого движений позволяет многие задачи квантовой химии свести к решению только электронного уравнения Шрёдингера и обычно выполняется для основных состояний молекул. Однако следует учитывать, что оно тем более справедливо, чем больше отличаются массы ядра и электрона. Приближение успешно работает при изучении свойств систем тяжелых ядер и может оказаться не совсем подходящим для легких ядер, в частности протонов. Последнее замечание важно для теории кислотно-основных реакций. Это приближение часто нарушается, когда возможно пересечение поверхностей потенциальной энергии различных электронных состояний. Энергия колебания ядер при этом становится соизмеримой с разностью энергий электронных состояний, что и является условием взаимодействия электронного и ядерного движений. Оно не справедливо для вырожденных электронных состояний любых молекулярных систем с нелинейным и симметричным пространственным строением.
🔍 Видео
06 03 окт 15 Прибл Борна ОппенгеймераСкачать

Урок 455. Уравнение ШрёдингераСкачать

Квантовая механика 41 - Уравнение Шредингера. Гамильтониан.Скачать

Лекция профессора Владислава Блатова «Основные приближения квантовой химии».Скачать

Степанов Н. Ф. - Квантовая химия - Волновая функцияСкачать
Новаковская Ю. В. - Строение молекул - Молекулярная задачаСкачать

Оператор Набла. Градиент. Дивергенция. Ротор. Лапласиан.Скачать

Лекция 1 (вторая часть)Скачать

Консультация по квантовой механике. Часть 10. "Эффект Зеемана. ЭПР и ЯМР"Скачать

Классические уравнения | уравнение Шрёдингера (координатное представление) | простейший выводСкачать

Атомная физика. Лекция 14. Атом водорода. Гамильтониан и решение уравнения Шредингера.Скачать

Структура материи 6: уравнение Шрёдингера. Зачем нужна квантовая механика – Виталий Бейлин | НаучпопСкачать

Введение к квантовую химиюСкачать

Теория Бора. Гипотеза де Бройля. Принцип неопределенности. Уравнение Шрёдингера.Скачать

Квантовая механика 49 - Реальна ли волновая функция?Скачать

Новаковская Ю. В. - Квантовая химия - Метод функционала плотностиСкачать

Воронина Е. Н. - Атомная физика. Семинары - МолекулаСкачать

Лучшая модель атома? [Минутка физики]Скачать
![Лучшая модель атома? [Минутка физики]](https://i.ytimg.com/vi/eybcxXiYJfc/0.jpg)