В поле z7 решить систему уравнений (5 видео)

Вычисления в полях вычетов

Рассмотрим некоторые особенности вычислений в полях вычетов. Найдем, например, определитель 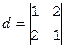, элементы которого суть вычеты из поля
(Z₃, +₃, ×₃). Если действовать «по науке», надо писать

Можно, однако, поступить проще. Будем считать элементы определителя обычными целыми числами из кольца Z, тогда d=1×1–2×2= –3.

Как найти для целого числа из Z соответствующий вычет из Z_n? Для этого надо к числу прибавить (или отнять от него) величину, кратную n, чтобы результат принадлежал множеству вычетов Z_n=<0,1,¼,n–1>. В данном случае прибавим 3 и получим –3+3=0 – тот же результат.

В дальнейшем станем действовать аналогично, к тому же не будем педантично ставить индекс +_n, ×_n около символов операций, обозначая их просто + и
× , если значение индекса n ясно из контекста.

Рассмотрим решение системы линейных уравнений над полем вычетов.

Пример. Решим над тремя полями: Q, Z₃, Z₅ систему уравнений A×X=B, где . т.е.

Заметим, что коэффициенты системы (0, 1 и 2), включая свободные члены, можно рассматривать не только как числа (т.е. элементы поля Q), но и как элементы интересующих нас конечных полей Z₃ и Z₅. В противном случае постановку задачи пришлось бы как-то изменять.

Решать систему будем по правилу Крамера. Вычислим над полем Q четыре определителя:

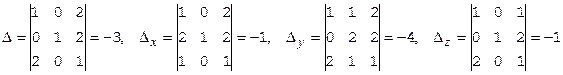
Значения неизвестных найдем по формулам Крамера: .

Приведем значения определителей в поле вычетов Z₃=, получим: D=0, D_x=2, D_y=2, D_z=2. Видим, что над этим полем система несовместна.

Приведем значения определителей в поле вычетов Z₅=: D=2, D_x=4, D_y=1, D_z=4. Значения неизвестных снова найдем по формулам Крамера: . Как понимать найденное значение неизвестной ? Дробь не является элементом поля Z₅, поэтому ее надо рассматривать как выражение, которое необходимо вычислить согласно правилам действий в этом поле: (поскольку произведение 2×3=6, а 6 в поле Z₅ переходит в 1). Итак, решение системы уравнений над полем Z₅ таково: x=2, y=3, z=2.

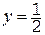
Сделаем проверку (символом Þ обозначен переход от целых чисел к вычетам по модулю 5). Первое уравнение: 1×2+2×2=6 Þ 1, второе уравнение: 1×3+2×2=7 Þ 2, третье уравнение: 2×2+1×2=6 Þ 1. Видим, что найденные значения вычетов удовлетворяют системе уравнений над полем Z₅.

Решим ту же систему над полем Z₃ методом Гаусса. Составим расширенную матрицу: . Если бы мы решали систему над полем рациональных чисел Q, то первым шагом выполнили бы операцию (3)–2×(1). В поле Z₃ коэффициенту –2 соответствует вычет 1, поэтому выполним операцию (3)+1×(1). В 1-ом столбце имеем 2+1×1=3Þ0, во 2-ом столбце сохранится 0, в третьем столбце 1+1×2=3Þ0, в столбце свободных членов 1+1×1=2, так что . В алгебраической форме 3-е уравнение этой системы имеет вид 0×x+0×y+0×z=2. Очевидно, что оно не имеет решения, поэтому система над полем Z₃ несовместна.

Найдем решение той же системы над полем Z₅ методом Гаусса. Вместо операции (3)–2×(1), с которой начинается решение этой системы над полем рациональных чисел Q, выполним операцию (3)+3×(1), поскольку в поле Z₅ коэффициенту –2 соответствует вычет 3. В 1-ом столбце получим 2+3×1=5Þ0, во 2-ом столбце сохранится 0, в третьем, в 3-ем столбце имеем 1+3×2=7Þ2, в столбце свободных членов 1+3×1=4. Таким образом, получим . 3-ю строку этой матрицы можно сократить (разделить) на 2: .

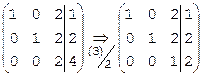
Теперь выполним операции (1)+3×(3) и (2)+3×(3) – в 1-й и во 2-й строках 3-го столбца получится 2+3×1=5Þ0, остальные элементы этих строк сохраняться: .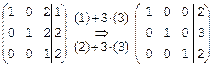

Видим, что получилось решение, ранее найденное по правилу Крамера: x=2, y=3, z=2.

Видео:Система уравнений. Метод алгебраического сложенияСкачать

Помогите с алгеброй. Поле вычетов по модулю

Здесь на сайте как-то кто-то писал решение к вот такой задачке

Решить систему уравнений в поле вычетов по модулю 7.

x + y + z = 1
4x + 2y + 3z = 1
x + 4y + 4z = 2

Вот собственно решение:

Значит, так. Поле вычетов по модулю 7 состоит всего из семи элементов:

При этом противоположные элементы будут выглядеть так:
-1 = 6
-2 = 5
-3 = 4
-4 = 3
-5 = 2
-6 = 1

Обратные элементы, соответственно, будут выглядеть так:
1/2 = 4
1/3 = 5
1/4 = 2
1/5 = 3
1/6 = 6

Разнообразные арифметические аксиомы ассоциативности, коммутативности и дистрибутивности сохраняются в неизменном виде.

Теперь можно решать исходную систему.

Из первого уравнения получаем:
x = 1-y-z = 1+6y+6z
Подставляем это в третье уравнение:
(1+6y+6z) + 4y + 4z = 2
1 + (6+4)y + (6+4)z = 2
1 + 3y + 3z = 2
1 + 3y + 3z + 6 = 2 + 6
3y + 3z = 1
y + z = 5
Подставляем это в первое уравнение:
x + 5 = 1
x + 5 + 2 = 1 + 2
x = 3
Подставляем это во второе уравнение:
4*3 + 2y + 3z = 1
5 + 2(y+z) + z = 1
5 + 2*5 + z = 1
5 + 3 + z = 1
1 + z = 1
z = 0
Тогда y = 5

Получаем ответ: x = 3, y = 5, z = 0

Подскажите пожалуйста, откуда взялось вот это :

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решение систем линейных уравнений

Эта страничка поможет решить Системы Линейных Алгебраических Уравнений (СЛАУ) методом Гаусса, матричным методом или методом Крамера, исследовать их на совместность (теорема Кронекера-Капелли), определить количество решений, найти общее, частное и базисные решения.

Введите коэффициенты при неизвестных в поля. Если Ваше уравнение имеет меньшее количество неизвестных, то оставьте пустыми поля при переменных, не входящих в ваше уравнение. Можно использовать дроби ( 13/31 ).