В линейном уравнении тренда у а0 а1 t параметр а0 характеризует (6 видео)

Содержание

Тенденция во временном ряду
Линейный тренд
Параметры тренда
В линейном уравнении тренда у а0 а1 t параметр а0 характеризует
Тест: Ответы на тест по эконометрике
Добавление отзыва к работе
🎥 Видео

Видео:Excel. Линия трендаСкачать

Тенденция во временном ряду

Синонимом тенденции в эконометрике является тренд. Одним из наиболее популярных способов моделирования тенденции временного ряда является нахождение аналитической функции, характеризующей зависимость уровней ряда от времени. Этот способ называется аналитическим выравниванием временного ряда.

Зависимость показателя от времени может принимать разные формы, поэтому находят различные функции: линейную, гиперболу, экспоненту, степенную функцию, полиномы различных степеней. Временной ряд исследуют аналогично линейной регрессии.

Параметры любого тренда можно определить обычным методом наименьших квадратов, используя в качестве фактора время t = 1, 2,…, n, а в качестве зависимой переменной используют уровни временного ряда. Для нелинейных трендов сначала проводят процедуру линеаризации.

К числу наиболее распространенных способов определения типа тенденции относят качественный анализ изучаемого ряда, построение и анализ графика зависимости уровней ряда от времени, расчет основных показателей динамики. В этих же целях можно часто используют и коэффициенты автокорреляции уровней временного ряда.

Видео:Эконометрика. Линейная парная регрессияСкачать

Линейный тренд

Тип тенденции определяют путем сравнения коэффициентов автокорреляции первого порядка. Если временной ряд имеет линейный тренд, то его соседние уровни yt и yt-1 тесно коррелируют. В таком случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть максимальный. Если временной ряд содержит нелинейную тенденцию, то чем сильнее выделена нелинейная тенденция во временном ряду, тем в большей степени будут различаться значения указанных коэффициентов.

Выбор наилучшего уравнения в случае, если ряд содержит нелинейную тенденцию, можно осуществить перебором основных видов тренда, расчета по каждому уравнению коэффициента корреляции и выбора уравнения тренда с максимальным значением коэффициента.

Параметры тренда

Наиболее простую интерпретацию имеют параметры экспоненциального и линейного трендов.

Параметры линейного тренда интерпретируют так: а — исходный уровень временного ряда в момент времени t = 0; b — средний за период абсолютный прирост уровней рада.

Параметры экспоненциального тренда имеют такую интерпретацию. Параметр а — это исходный уровень временного ряда в момент времени t = 0. Величина exp(b) — это средний в расчете на единицу времени коэффициент роста уровней ряда.

По аналогии с линейной моделью расчетные значения уровней рада по экспоненциальному тренду можно определить путем подстановки в уравнение тренда значений времени t = 1,2,…, n, либо в соответствии с интерпретацией параметров экспоненциального тренда: каждый последующий уровень такого ряда есть произведение предыдущего уровня на соответствующий коэффициент роста

При наличии неявной нелинейной тенденции нужно дополнять описанные выше методы выбора лучшего уравнения тренда качественным анализом динамики изучаемого показателя, для того, чтобы избежать ошибок спецификации при выборе вида тренда. Качественный анализ предполагает изучение проблем возможного наличия в исследуемом ряду поворотных точек и изменения темпов прироста, начиная с определенного момента времени под влиянием ряда факторов, и т. д. В том случае если уравнение тренда выбрано неправильно при больших значениях t, результаты прогнозирования динамики временного ряда с использованием исследуемого уравнения будут недостоверными по причине ошибки спецификации.

Иллюстрация возможного появления ошибки спецификации приведем на рисунке

Если оптимальной формой тренда является парабола, в то время как на самом деле имеет место линейная тенденция, то при больших t парабола и линейная функция естественно будут по разному описывать тенденцию в уровнях ряда.

Источник: Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М: Финансы и статистика, 2002. – 344 с.

Видео:Парная регрессия: линейная зависимостьСкачать

В линейном уравнении тренда у а0 а1 t параметр а0 характеризует

Пример 14.6. Построим линейный тренд процентных ставок по кредитам на основе статистических данных, опубликованных в Бюллетене банковской статистики № 4 (47) за 1997 г. [c.612]

Вторым этапом является поиск значений параметров уравнения. Параметры трендовых моделей определяются с помощью системы нормальных уравнений. В случае применения линейного тренда используют следующую систему уравнений, которую решают способом наименьших квадратов [c.612]

Пример 14.7. Предполагая наличие циклических колебаний, проведем гармонический анализ динамики отклонений от линейного тренда данных о ставках по кредитам (у, — у,). [c.617]

Линейный тренд хорошо отражает тенденцию изменений при действии множества разнообразных факторов, изменяющихся различным образом по разным закономерностям. Равнодействующая этих факторов при взаимопогашении особенностей отдельных фак- [c.322]

При b = 1 имеем линейный тренд, b = 2 — параболический и т.п. Степенная форма — гибкая, пригодная для отображения изменений с разной мерой пропорциональности изменений во времени. Жестким условием является обязательное прохождение через начало координат при t = 0, у = 0. Можно усложнить форму тренда у = а + th или у = а + th, но эти уравнения нельзя логарифмировать, трудно вычислять параметры, и они крайне редко применяются. [c.325]

Таблица 9.4 Проверка гипотезы о линейном тренде индекса цен (1990 г. = 100%)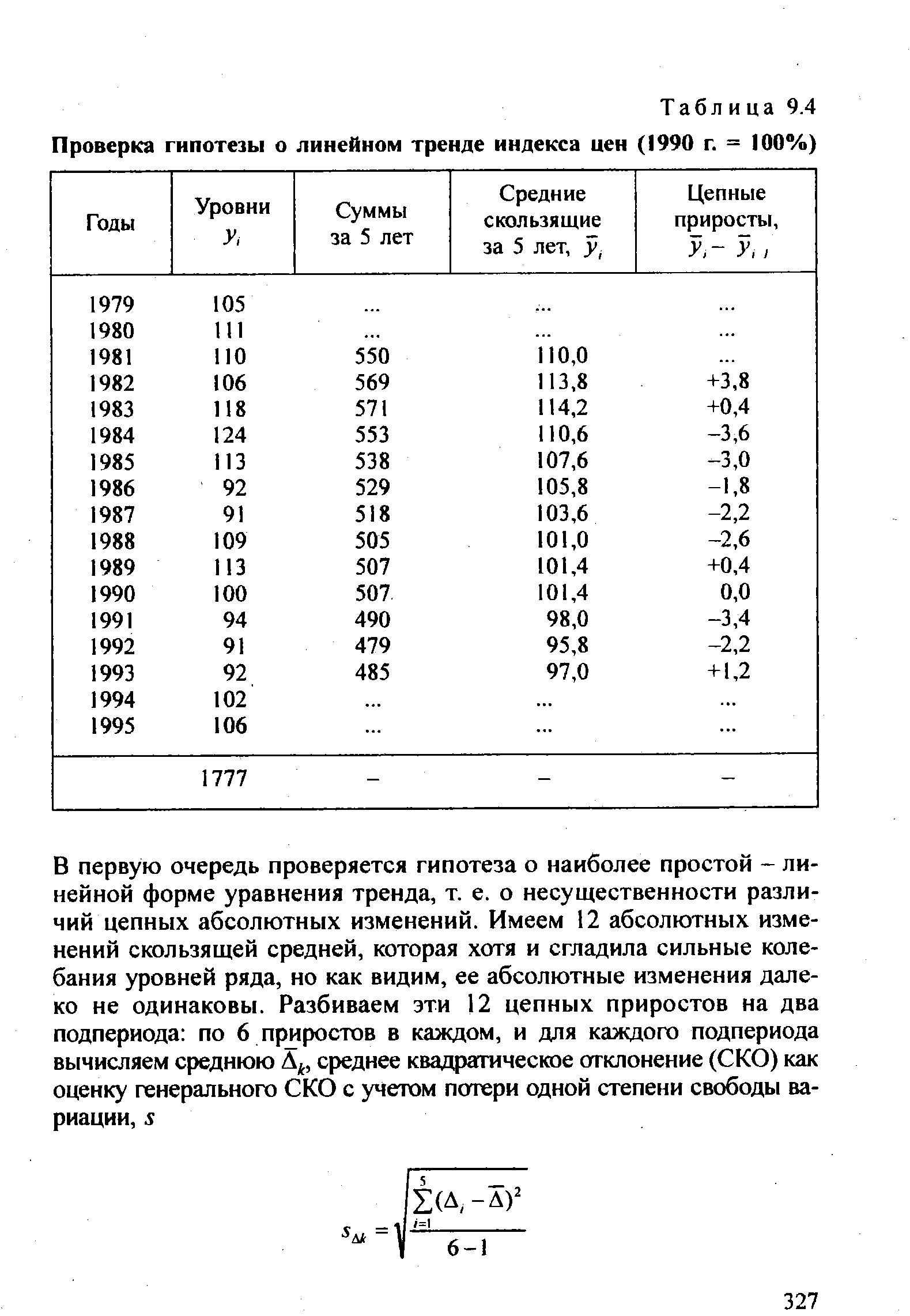

В линейном уравнении тренда у а0 а1 t параметр а0 характеризует

Для линейного тренда нормальные уравнения МНК имеют вид [c.329]

В формуле (9.33) суммирование от = -(л-1) 2до/ = (л- 1) 2 в целом формула (9.33) аналогична формуле для линейного тренда (9.29). [c.331]

Согласно формуле (9.29) параметры линейного тренда равны а = 1894/11 = 172,2 ц/га 2>Л= 486/110 = 4,418 ц/га. Уравнение линейного тренда имеет вид у = 172,2 + 4,418/, где ( = 0 в 1987 г. Это означает, что средний фактический и выравненный уровень, отнесенный к середине периода, т.е. к 1991 г., равен 172 ц с 1 га, а среднегодовой прирост составляет 4,418 ц/га в год. [c.332]

Поскольку по данным табл. 9.4, уже было установлено, что тренд имеет линейную форму, проводим расчет среднегодового абсолютного прироста, т. е. параметра Ъ уравнения линейного тренда сколь- [c.336]

Колеблемость умеренная, не сильная. Для сравнения приводим показатели (без расчета) по колебаниям урожайности картофеля, данные таблиц 9.1 и 9.5 — отклонение от линейного тренда s(t) = 14,38 ц с 1 га, v(t) = 8,35%. [c.342]

Средняя ошибка прогноза положения линейного тренда на год (момент) с номером tk вычисляется по формулам [c.358]

Для получения достаточно надежных границ прогноза положения тренда, скажем, с вероятностью 0,9 того, что ошибка будет не более указанной, следует среднюю ошибку умножить на величину /-критерия Стьюдента при указанной вероятности (или значимости 1 — 0,9 = 0,1) и при числе степеней свободы, равном, для линейного тренда, N- 2, т. е. 15. Эта величина равна 1,753. Получаем предельную с данной вероятностью ошибку [c.359]

Другим приемом измерения корреляции в рядах динамики может служить корреляция между теми из цепных показателей рядов, которые являются константами их трендов. При линейных трендах — это цепные абсолютные приросты. Вычислив их по исходным рядам динамики (axl, ayi), находим коэффициент корреляции между абсолютными изменениями по формуле (9.52) или, что более точно, по формуле (9.51), так как средние изменения не равны нулю в отличие от средних отклонений от трендов. Допустимость данного способа основана на том, что разность между соседними уровнями в основном состоит из колебаний, а доля тренда в них невелика, следовательно, искажение корреляции от тренда очень большое при кумулятивном эффекте на протяжении длительного периода, весьма мало — за каждый год в отдельности. Однако нужно помнить, что это справедливо лишь для рядов с с-показателем, существенно меньшим единицы. В нашем примере для ряда урожайности с-по-казатель равен 0,144, для себестоимости он равен 0,350. Коэффициент корреляции цепных абсолютных изменений составил 0,928, что очень близко к коэффициенту корреляции отклонений от трендов. [c.366]

В одном из предыдущих примеров мы рассмотрели прогноз по объему производства за два месяца некой компании из Дублина. Были получены оценки на 1997 год, при этом использовался линейный тренд и метод сложения. Прогнозные значения даны в тоннах [c.213]

Значения k для оценки доверительных интервалов прогноза относительно линейного тренда с вероятностью 0,8 [c.33]

Адаптивное моделирование линейного тренда с помощью экспоненциальных скользящих средних. [c.165]

Алгоритм вычисления параметров линейного тренда [c.169]

Вычислить в первом приближении параметры линейного тренда [c.169]

Определить окончательные значения параметров линейного тренда [c.169]

ЕМА ошибок могут ухудшить качество прогноза. В этом случае при расчете параметров линейного тренда нужно остановиться на шаге 2 этого алгоритма. [c.169]

Когда мы рассматриваем сектор рынка, соответствующий долгосрочным сделкам, вероятно, следует признать, что определяющее влияние на цены оказывают здесь такие экзогенные факторы, как обменные курсы и процентные ставки, показатели экономического роста, тенденции (тренды) цен и показателей прибыли. Поведение рынка здесь удовлетворительно описывается так называемой гипотезой эффективного рынка, согласно которой в каждый момент вся доступная информация о текущих и будущих событиях дисконтируется в текущие цены рынка, так что изменения цен бывают вызваны только поступающей свежей информацией. Напротив, в краткосрочной перспективе появляются новые возможности для прогнозов, связанные с учетом регулирования платежей, обратных связей и многочисленных технических и структурных факторов. Старые парадигмы финансовой науки типа модели случайного блуждания или гипотезы эффективного рынка внушают нам представление о том, что финансовые рынки склонны относительно плавно и разумно приспосабливаться к поступающей информации. В этом круге идей вполне убедительно выглядят описания поведения рынка на основе линейных зависимостей и законов обращения трендов (стационарности). Однако драматические обвалы рынка при отсутствии существенных изменений информации, резкие изменения условий доступа и сроков при пересечении компанией какого-то невидимого порога в кредитной сфере — все это проявления нелинейности. Действительность показывает, что поведение финансовых рынков едва ли может быть описано линейными трендами. [c.15]

LN — линейный тренд, сезонность не учитывается [c.68]

Если считать, что изменения цен, вопреки соображениям эффективности на продолжительных отрезках времени, определяются многочисленными и часто нелинейными обратными связями, то на основе теории хаоса можно построить улучшенные модели, описывающие влияние прошлого на настоящее (см. [213]-[216]). Драматические обвалы рынка при отсутствии существенных изменений информации, резкие изменения условий доступа и сроков при пересечении компанией какого-то невидимого порога в кредитной сфере — все это проявления нелинейности. Реальное поведение финансовых рынков, скорее, противоречит правилам обращения линейных трендов, чем подтверждает их. [c.74]

Метод последовательных разностей заключается в следующем если ряд содержит линейный тренд, тогда исходные данные заменяются первыми разностями [c.139]

Значения Лу не имеют четко выраженной тенденции, они варьируют вокруг среднего уровня, что означает наличие в ряде динамики линейного тренда (линейной тенденции). Аналогичный вывод можно сделать и по ряду х абсолютные приросты не имеют систематической направленности, они примерно стабильны, а следовательно, ряд характеризуется линейной тенденцией. [c.145]

Постройте уравнение линейного тренда и дайте интерпретацию его параметров, [c.163]

Это привело к идее измерения корреляции не самих уровней х, иу а первых разностей Дх, = х, — , ,, 6у, — у, — у. (при линейных трендах). В общем случае было признано необходимым коррелировать отклонения от трендов (за вычетом циклической компоненты) Еу —у, — %, Ех = х, — %, (у,,% — тренды временных рядов). [c.19]

На графике рис. 5.3 наглядно видно наличие возрастающей тенденции. Возможно существование линейного тренда. [c.236]

Параметры линейного тренда можно интерпретировать так а — начальный уровень временного ряда в момент времени t = 0 b — средний за период абсолютный прирост уровней ряда. Применительно к данному временному ряду можно сказать, что темпы роста номинальной месячной заработной платы за 10 месяцев 1999 г. изменялись от уровня 82,66% со средним за месяц абсолютным приростом, равным 4,72 проц. пункта. Расчетные по линейному тренду значения уровней временного ряда определяются двумя способами. Во-первых, можно последовательно подставлять в найденное уравнение тренда значения / = 1, 2. л, т.е. [c.237]

Во-вторых, в соответствии с интерпретацией параметров линейного тренда каждый последующий уровень ряда есть сумма предыдущего уровня и среднего цепного абсолютного прироста, т. е. [c.238]

Таким образом, начальный уровень ряда в соответствии с уравнением экспоненциального тренда составляет 83,96 (сравните с начальным уровнем 82,66 в линейном тренде), а средний цепной коэффициент роста — 1,046. Следовательно, можно сказать, что темпы роста номинальной месячной заработной платы за 10 месяцев 1999 г. изменялись от уровня 83,96% со средним за месяц цепным темпом роста, равным 104,6%. Иными словами, средний за месяц цепной темп прироста временного ряда составил 4,6%. [c.238]

Шаг 4. Определим компоненту Т данной модели. Для этого проведем аналитическое выравнивание ряда (Т+ Е) с помощью линейного тренда. Результаты аналитического выравнивания следующие [c.244]

Такой переход позволяет определить знак изменения курса валюты, что достаточно для достижения прибыли от операций с ней. При наличии у временного ряда линейного тренда могут быть применены и другие методы адаптивного прогнозирования Брауна, Хольта и Тей-ла-Вейджа. [c.676]

Рассчитанные по уравнениям трендов уровни записаны в трех последних графах табл. 9.5. Как видно по этим данным, расчетные значения уровней по всем трем видам трендов различаются ненамного, так как и ускорение параболы, и темп роста экспоненты невелики. Существенное отличие имеет парабола — рост уровней с 1995 г. прекращается, в то время как при линейном тренде уровни растут и далее, а при экспоненте их рост ускоряется. Поэтому для прогнозов на будущее эти три тренда неравноправны при экстраполяции параболы на будущие годы уровни резко разойдутся с прямой и экспонентой, что видно из табл. 9.6. В этой таблице представлена распечатка решения на ПЭВМ по программе Statgraphi s тех же трех трендов. Отличие их свободных членов от приведенных выше объясняется тем, что программа нумерует года не от середины, а от начала, так что свободные члены трендов относятся к 1986 г., для которого / = 0. Уравнение экспоненты на распечатке оставлено в логарифмированном виде. Прогноз сделан на 5 лет вперед, т.е. до 2001 г.. При изменении начала координат (отсчета времени) в уравнении параболы меняется и средний абсолютный прирост, параметр Ъ, так как в результате отрицательного ускорения [c.332]

Для определения параметров линейного тренда по методу наименьших квадратов используется статистическая функция ЛИНЕЙН, для определения экспоненциального тренда -ЛГРФПРИБЛ. Порядок вычисления был рассмотрен в 1-м разделе практикума. В качестве зависимой переменной в данном примере выступает время (г = 1, 2,. . л). Приведем результаты вычисления функций ЛИНЕЙН и ЛГРФПРИБЛ (рис. 4.2 и 4.3). [c.151]

Видео:Excel для полных чайников Урок 16 Линия трендаСкачать

Тест: Ответы на тест по эконометрике

Тема: Ответы на тест по эконометрике

Аддитивная модель содержит компоненты в виде …

комбинации слагаемых и сомножителей

слагаемых

В линейной регрессии Y=b0+b1X+e параметрами уравнения регрессии являются: (неск)

В правой части приведенной формы системы одновременных уравнений, построенной по перекрестным данным (cross-section data) без учета временных факторов, могут стоять _______ переменные.

экзогенные

В стационарном временном ряде трендовая компонента …

имеет линейную зависимость от времени

отсутствует

имеет нелинейную зависимость от времени

Величина коэффициента детерминации … (неск)

характеризует долю дисперсии зависимой переменной y, объясненную уравнением, в ее общей дисперсии

рассчитывается для оценки качества подбора уравнения регрессии

характеризует долю дисперсии остаточной величины в общей дисперсии зависимой переменной у

оценивает значимость каждого из факторов, включенных в уравнение регрессии

Величина коэффициента регрессии показывает …

среднее изменение фактора при изменении результата на одну единицу измерения

на сколько процентов изменится результат при изменении фактора на 1 %

значение тесноты связи между фактором и результатом

среднее изменение результата при изменении фактора на одну единицу измерения

Величина коэффициента эластичности показывает …

на сколько процентов изменится в среднем результат при изменении фактора на 1%

во сколько раз изменится в среднем результат при изменении фактора в два раза

предельно допустимое изменение варьируемого признака

предельно возможное значение результата

Временным рядом является совокупность значений …

экономического показателя за несколько последовательных моментов (периодов) времени

последовательных моментов (периодов) времени и соответствующих им значений экономического показателя

экономических однотипных объектов по состоянию на определенный момент времени

экономического показателя для однотипных объектов на определенный момент времени

Выберите верные утверждения по поводу структурной формы системы эконометрических уравнений:

каждое уравнение системы может рассматриваться в качестве отдельного уравнения регрессии зависимости одной переменной от группы факторов

система регрессионных уравнений, матрица коэффициентов которых симметрична

эндогенные переменные в одних уравнениях могут выступать в роли независимых переменных в других уравнениях системы

система одновременных уравнений описывает реальное экономическое явление или процесс

Гомоскедастичность остатков подразумевает …

рост дисперсии остатков с увеличением значения фактора

максимальную дисперсию остатков при средних значениях фактора

уменьшение дисперсии остаток с уменьшением значения фактора

одинаковую дисперсию остатков при каждом значении фактора

Диаграмма рассеяния указывает на нелинейную зависимость. В этом случае следует осуществить … (неск)

расчет линейного коэффициента корреляции и использование линейной модели

включение в модель дополнительных факторных признаков

визуальный подбор функциональной зависимости нелинейного характера, соответствующего структуре точечного графика

подбор преобразования переменных, дающего наибольшее по абсолютной величине значение коэффициента парной корреляции

Для линейного уравнения регрессии у = а + bx + e метод наименьших квадратов используется при оценивании параметров…(неск)

Для расчета критического значения распределения Стьюдента служат следующие параметры:

количество зависимых переменных

объем выборки и количество объясняющих переменных

уровень значимости

К классам эконометрических моделей относятся: (неск)

системы нормальных уравнений

корреляционно – регрессионные модели

модели временных рядов

Компонентами временного ряда являются: (неск)

циклическая (сезонная) компонента

тренд

Корреляция подразумевает наличие связи между …

результатом и случайными факторами

переменными

Косвенный метод наименьших квадратов применим для …

неидентифицируемой системы уравнений

неидентифицируемой системы рекурсивных уравнений

любой системы одновременных уравнений

идентифицируемой системы одновременных уравнений

Коэффициент детерминации рассчитывается для оценки качества…

подбора уравнения регрессии

параметров уравнения регрессии

факторов, не включенных в уравнение регрессии

Коэффициент парной корреляции характеризует тесноту ____ связи между _____ переменными.

линейной … двумя

Критические значения критерия Стьюдента определяются по…

двум степеням свободы

трем и более степеням свободы

уровню значимости и одной степени свободы

Метод наименьших квадратов используется для оценивания …

величины коэффициента детерминации

параметров линейной регрессии

величины коэффициента корреляции

средней ошибки аппроксимации

Нелинейным является уравнение регрессии нелинейное относительно входящих в него …

факторов

Несмещенность оценки характеризует …

равенство нулю математического ожидания остатков

наименьшую дисперсию остатков

ее зависимость от объема выборки

увеличение точности ее вычисления с увеличением объема выборки

Обобщенный метод наименьших квадратов применяется в случае…

автокорреляции остатков

Под автокорреляцией уровней временного ряда подразумевается _____ зависимость между последовательными уровнями ряда.

корреляционная

При выполнении предпосылок МНК оценки параметров регрессии обладают свойствами: (неск)

несмещенность

эффективность

Предпосылками МНК являются … (неск)

случайные отклонения коррелируют друг с другом

гетероскедастичность случайных отклонений

случайные отклонения являются независимыми друг от друга

дисперсия случайных отклонений постоянна для всех наблюдений

Примерами фиктивных переменных могут служить: (неск)

пол

образование

Примером нелинейной зависимости экономических показателей является …

зависимость объема продаж от недели реализации, выраженная линейным трендом

линейная зависимость затрат на производство от объема выпуска продукции

линейная зависимость выручки от величины оборотных средств

классическая гиперболическая зависимость спроса от цены

Принципиальные сложности применения систем эконометрических уравнений связаны с ошибками…

однородности выборочной совокупности

спецификации модели

определения случайных воздействий

Система эконометрических уравнений включает в себя следующие переменные:

эндогенные

экзогенные

Способами определения структуры временного ряда являются: (неск)

анализ автокорреляционной функции

расчет коэффициентов корреляции между объясняющими переменными

построение коррелограммы

агрегирование данных за определенный промежуток времени

Среди нелинейных эконометрических моделей рассматривают следующие классы нелинейных уравнений: …

внутренне нелинейные

внутреннее линейные

Структурной формой модели называется система ____ уравнений.

взаимосвязанных

Тенденция временного ряда характеризует совокупность факторов, …

оказывающих сезонное воздействие

оказывающих единовременное влияние

оказывающих долговременное влияние и формирующих общую динамику изучаемого показателя

не оказывающих влияние на уровень ряда

Укажите верные характеристики коэффициента эластичности:

коэффициент эластичности показывает на сколько процентов изменится значение результирующего фактора при изменении на один процент объясняющего фактора

коэффициент эластичности является постоянной величиной для всех видов моделей

коэффициент эластичности показывает на сколько изменится значение результирующего фактора при изменении объясняющего фактора на одну единицу

по значению коэффициента эластичности можно судить о силе связи объясняющего фактора с результирующим

Укажите последовательность этапов оценки параметров нелинейной регрессии Y = a + b*X + c*X².

3 оцениваются параметры регрессии b0, b1, b2

1 выполняется замена переменной X2 на Z

2 задается спецификация модели в виде Y = b₀ + b₁*X +b₂*Z, где b₀ = a; b₁ = b; b₂ =c

4 определяются исходные параметры из тождеств: a = b₀; b = b₁; c = b₂

Укажите последовательность этапов проведения теста Голдфелда-Квандта для парной линейной регрессии.

4 вычисление статистики Фишера

1 упорядочение наблюдений по возрастанию значений объясняющей переменной

3 оценка сумм квадратов отклонений для регрессий по k-первым и k-последним наблюдений

2 оценка регрессий для k-первых и k-последних наблюдений

Укажите справедливые утверждения по поводу критерия Дарбина-Уотсона: (неск)

позволяет проверить гипотезу о наличии автокорреляции первого порядка

изменяется в пределах от 0 до 4

равен 0 в случае отсутствия автокорреляции

применяется для проверки гипотезы о наличии гетероскедастичности остатков

Укажите существующие классы эконометрических систем: (неск)

система нормальных уравнений

система стандартных уравнений

система одновременных уравнений

система независимых уравнений

Укажите требования к факторам, включаемым в модель множественной линейной регрессии: (неск)

между факторами не должна существовать высокая корреляция

факторы должны быть количественно измеримы

факторы должны иметь одинаковую размерность

факторы должны представлять временные ряды

Установите соответствие между названием модели и видом ее уравнения:

3 y = ab x *e;

Установите соответствие между наименованиями элементов уравнения Y=b0+b1X+e и их буквенными обозначениями:

1. параметры регрессии

2. объясняющая переменная

3. объясняемая переменная

4. случайные отклонения

3 Y

4 e

1 b0, b1

2 X

Установите соответствие между эконометрическими терминами и их определениями.

1. автокорреляция уровней временного ряда

2. коэффициент автокорреляции уровней временного ряда

3. автокорреляционная функция

3 последовательность коэффициентов автокорреляции первого, второго и т.д. порядков

4 график зависимости значений автокорреляционной функции от величины лага

1 корреляционная зависимость между последовательными уровнями ряда

2 коэффициент линейной корреляции между последовательными уровнями

Фиктивными переменными в уравнении множественной регрессии являются …

качественные переменные, преобразованные в количественные

комбинации из включенных в уравнение регрессии факторов, повышающие адекватность модели

переменные, представляющие простейшие функции от уже включенных в модель переменных

дополнительные количественные переменные, улучшающие решение

Число степеней свободы общей, факторной и остаточной дисперсий связано …

только с числом единиц совокупности

с числом единиц совокупности и видом уравнения регрессии

характером исследуемых переменных

только с видом уравнения регрессии

Число степеней свободы связано с числом … (неск)

единиц совокупности (количеством наблюдений)

видом уравнения регрессии

раздел экономической теории, связанный с анализом статистической информации

специальный раздел математики, посвященный анализу экономической информации

наука, которая осуществляет качественный анализ взаимосвязей экономических явлений и процессов

наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

Чтобы скачать бесплатно Тесты на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Тесты для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Если Тест, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

Видео:Прогнозирование в Excel с помощью линий трендаСкачать