В линейном уравнении парной регрессии y a bx e переменными являются (5 видео)

Основы линейной регрессии

Содержание

Что такое регрессия?
Линия регрессии
Метод наименьших квадратов
Предположения линейной регрессии
Аномальные значения (выбросы) и точки влияния
Гипотеза линейной регрессии
Оценка качества линейной регрессии: коэффициент детерминации R 2
Применение линии регрессии для прогноза
Простые регрессионные планы
Пример: простой регрессионный анализ
Задача исследования
Просмотр результатов
Коэффициенты регрессии
Распределение переменных
Диаграмма рассеяния
Критерии значимости
Ответы на тесты по эконометрике
Тест: Ответы на тест по эконометрике
Добавление отзыва к работе
Эконометрика
📸 Видео

Видео:Парная регрессия: линейная зависимостьСкачать

Что такое регрессия?

Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.

Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.

Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).

Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).

Видео:Парная и множественная линейная регрессияСкачать

Линия регрессии

Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:

x называется независимой переменной или предиктором.

Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»

a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.

Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.

Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)

Видео:Эконометрика. Линейная парная регрессияСкачать

Метод наименьших квадратов

Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).

Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).

Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).

Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.

Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.

Видео:Регрессия - как строить и интерпретировать. Примеры линейной и множественной регрессии.Скачать

Предположения линейной регрессии

Итак, для каждой наблюдаемой величины остаток равен разнице и соответствующего предсказанного Каждый остаток может быть положительным или отрицательным.

Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:

Между и существует линейное соотношение: для любых пар данные должны аппроксимировать прямую линию. Если нанести на двумерный график остатки, то мы должны наблюдать случайное рассеяние точек, а не какую-либо систематическую картину.

Остатки нормально распределены с нулевым средним значением;

Остатки имеют одну и ту же вариабельность (постоянную дисперсию) для всех предсказанных величин Если нанести остатки против предсказанных величин от мы должны наблюдать случайное рассеяние точек. Если график рассеяния остатков увеличивается или уменьшается с увеличением то это допущение не выполняется;

Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).

Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Аномальные значения (выбросы) и точки влияния

«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).

Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.

И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).

При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.

Видео:Метод наименьших квадратов. Парная регрессия расчет без Excel @economc #МНК #регрессия #корреляцияСкачать

Гипотеза линейной регрессии

При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.

Если угловой коэффициент линии равен нулю, между и нет линейного соотношения: изменение не влияет на

Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:

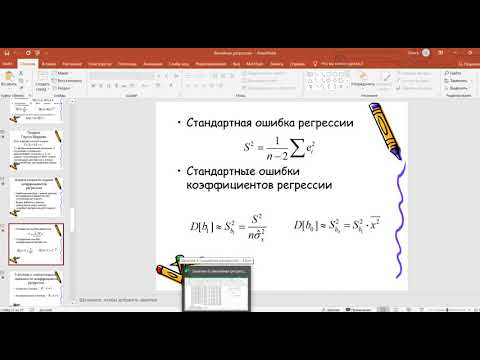
Вычислить статистику критерия, равную отношению , которая подчиняется распределению с степенями свободы, где стандартная ошибка коэффициента

— оценка дисперсии остатков.

Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.

Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :

где процентная точка распределения со степенями свободы что дает вероятность двустороннего критерия

Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.

Для больших выборок, скажем, мы можем аппроксимировать значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)

Видео:Уравнение парной линейной регрессии с помощью Анализа ДанныхСкачать

Оценка качества линейной регрессии: коэффициент детерминации R 2

Из-за линейного соотношения и мы ожидаем, что изменяется, по мере того как изменяется , и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.

Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.

Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R 2 (в парной линейной регрессии это величина r 2 , квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.

Разность представляет собой процент дисперсии который нельзя объяснить регрессией.

Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.

Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Применение линии регрессии для прогноза

Можно применять регрессионную линию для прогнозирования значения по значению в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).

Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение путем подстановки этого значения в уравнение линии регрессии.

Итак, если прогнозируем как Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины в популяции.

Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.

Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.

Видео:Что такое линейная регрессия? Душкин объяснитСкачать

Простые регрессионные планы

Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P , например, 7, 4 и 9, а план включает эффект первого порядка P , то матрица плана X будет иметь вид

а регрессионное уравнение с использованием P для X1 выглядит как

Если простой регрессионный план содержит эффект высшего порядка для P , например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:

а уравнение примет вид

Y = b 0 + b 1 P 2

Сигма -ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X . При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X , а работать только с регрессионным уравнением.

Видео:Парный линейный регрессионный анализСкачать

Пример: простой регрессионный анализ

Этот пример использует данные, представленные в таблице:

Рис. 3. Таблица исходных данных.

Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:

Рис. 4. Таблица спецификаций переменных.

Задача исследования

Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 ( Pt_Poor ) как зависимую переменную.

Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 ( Pop_Chng ) как переменную-предиктор.

Просмотр результатов

Коэффициенты регрессии

Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.

На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374 . Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p . Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.

Распределение переменных

Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor .

Рис. 6. Гистограмма переменной Pt_Poor.

Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»

Рис. 7. Гистограмма переменной Pt_Poor.

Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.

Диаграмма рассеяния

Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.

Рис. 8. Диаграмма рассеяния.

Диаграмма рассеяния показывает явную отрицательную корреляцию ( -.65 ) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.

Критерии значимости

Рис. 9. Таблица, содержащая критерии значимости.

Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor , p .

На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.

Видео:Парная нелинейная регрессияСкачать

Ответы на тесты по эконометрике

Q=………..min соответствует методу наименьших квадратов

Автокорреляция — это корреляционная зависимость уровней ряда от предыдущих значений.

Автокорреляция имеется когда каждое следующее значение остатков

Аддитивная модель временного ряда имеет вид: Y=T+S+E

Атрибутивная переменная может употребляться, когда: независимая переменная качественна;

В каких пределах изменяется коэффициент детерминанта: от 0 до 1.

В каком случае модель считается адекватной Fрасч>Fтабл

В каком случае рекомендуется применять для моделирования показателей с увелич. ростом параболу если относительная величина…неограниченно

В результате автокорреляции имеем неэффективные оценки параметров

В хорошо подобранной модели остатки должны иметь нормальный закон

В эконометрическом анализе Xj рассматриваются как случайные величины

Величина доверительного интервала позволяет установить предположение о том, что: интервал содержит оценку параметра неизвестного.

Величина рассчитанная по формуле r=…является оценкой парного коэф. Корреляции

Внутренне нелинейная регрессия — это истинно нелинейная регрессия, которая не может быть приведена к линейной регрессии преобразованием переменных и введением новых переменных.

Временной ряд — это последовательность значений признака (результативного переменного), принимаемых в течение последовательных моментов времени или периодов.

Выберете авторегрессионную модель Уt=a+b0x1+Ɣyt-1+ƹt

Выберете модель с лагами Уt= a+b0x1…….(самая длинная формула)

Выборочное значение Rxy не > 1, |R|

Гомоскидастичность – это когда дисперсия остатков постоянна и одинакова для всех … наблюдений.

Дисперсия — показатель вариации.

Для определения параметров неиденцифицированной модели применяется.: не один из сущ. методов применить нельзя

Для определения параметров сверх иденцифицированной модели примен.: применяется. 2-х шаговый МНК

Для определения параметров структурную форму модели необходимо преобразовать в приведенную форму модели

Для определения параметров точно идентифицируемой модели: применяется косвенный МНК;

Для оценки … изменения y от x вводится: коэффициент эластичности:

Для парной регрессии ơ²b равно ….(xi-x¯)²)

Для проверки значимости отдельных параметров регрессии используется: t-тест.

Для регрессии y=a+bx из n наблюдений интервал доверия (1-а)% для коэф. b составит b±t…….·ơb

Для регрессии из n наблюдений и m независимых переменных существует такая связь между R² и F..=[(n-m-1)/m]( R²/(1- R²)]

Доверительная вероятность – это вероятность того, что истинное значение результативного показателя попадёт в расчётный прогнозный интервал.

Допустим что для описания одного экономического процесса пригодны 2 модели. Обе адекватны по f критерию фишера. какой предоставить преимущество, у той у кот.: большее значения F критерия

Допустим, что зависимость расходов от дохода описывается функцией y=a+bx среднее значение у=2…равняется 9

Если Rxy положителен, то с ростом x увеличивается y.

Если в уравнении регрессии имеется несущественная переменная, то она обнаруживает себя по низкому значению T статистки

Если качественный фактор имеет 3 градации, то необходимое число фиктивных переменных 2

Если коэффициент корреляции положителен, то в линейной модели с ростом х увеличивается у

Если мы заинтересованы в использовании атрибутивных переменных для отображения эффекта разных месяцев мы должны использовать 11 атрибутивных методов

Если регрессионная модель имеет показательную зависимость, то метод МНК применим после приведения к линейному виду.

Зависимость между коэффициентом множественной детерминации (D) и корреляции (R) описывается следующим методом R=√D

Значимость уравнения регрессии — действительное наличие исследуемой зависимости, а не просто случайное совпадение факторов, имитирующее зависимость, которая фактически не существует.

Значимость уравнения регрессии в целом оценивают: -F-критерий Фишера

Значимость частных и парных коэф. корреляции поверен. с помощью: -t-критерия Стьюдента

Интеркорреляция и связанная с ней мультиколлинеарность — это приближающаяся к полной линейной зависимости тесная связь между факторами.

Какая статистическая характеристика выражается формулой R²=…коэффициент детерминации

Какая статистическая хар-ка выражена формулой : r_xy=Ca(x;y) разделить на корень Var(x)*Var(y): коэффициент. корреляции

Какая функция используется при моделировании моделей с постоянным ростом степенная

Какие точки исключаются из временного ряда процедурой сглаживания и в начале, и в конце.

Какое из уравнений регрессии является степенным y=a˳aͯ¹a

Классический метод к оцениванию параметров регрессии основан на: – метод наименьших квадратов (МНК)

Количество степеней свободы для t статистики при проверки значимости параметров регрессии из 35 наблюдений и 3 независимых переменных 31;

Количество степеней свободы знаменателя F-статистики в регрессии из 50 наблюдений и 4 независимых переменных: 45

Компоненты вектора Ei имеют нормальный закон

Корреляция — стохастическая зависимость, являющаяся обобщением строго детерминированной функциональной зависимости посредством включения вероятностной (случайной) компоненты.

Коэффициент автокорреляции: характеризует тесноту линейной связи текущего и предстоящего уровней ряда

Коэффициент детерминации — показатель тесноты стохастической связи в общем случае нелинейной регрессии

Коэффициент детерминации – это величина, которая характеризует связь между зависимыми и независимыми переменными.

Коэффициент детерминации – это квадрат множественного коэффициента корреляции

Коэффициент детерминации – это: величина, которая характеризует связь между независимой и зависимой (зависящей) переменными;

Коэффициент детерминации R показывает долю вариаций зависимой переменной y, объяснимую влиянием факторов, включаемых в модель.

Коэффициент детерминации изменяется в пределах: – от 0 до 1

Коэффициент доверия — это коэффициент, который связывает линейной зависимостью предельную и среднюю ошибки, выясняет смысл предельной ошибки, характеризующей точность оценки, и является аргументом распределения (чаще всего, интеграла вероятностей). Именно эта вероятность и есть степень надежности оценки.

Коэффициент доверия (нормированное отклонение) — результат деления отклонения от среднего на стандартное отклонение, содержательно характеризует степень надежности (уверенности) полученной оценки.

Коэффициент корелляции Rxy используется для определения полноты связи X и Y.

Коэффициент корелляции меняется в пределах : от -1 до 1

Коэффициент корелляции равный 0 означает, что: –отсутствует линейная связь.

Коэффициент корелляции равный 1 означает, что: -существует функциональная зависимость.

Коэффициент корреляции используется для: определения тесноты связи между случайными величинами X и Y;

Коэффициент корреляции рассчитывается для измерения степени линейной взаимосвязи между двумя случайными переменными.

Коэффициент линейной корреляции — показатель тесноты стохастической связи между фактором и результатом в случае линейной регрессии.

Коэффициент регрессии — коэффициент при факторной переменной в модели линейной регрессии.

Коэффициент регрессии b показывает: на сколько единиц увеличивается y, если x увеличивается на 1.

Коэффициент регрессии изменяется в пределах: применяется любое значение ; от 0 до 1; от -1 до 1;

Коэффициент эластичности измеряется в: неизмеримая величина.

Критерий Дарвина-Чотсона применяется для: – отбора факторов в модель; или – определения автокорреляции в остатках

Критерий Стьюдента — проверка значимости отдельных коэффициентов регрессии и значимости коэффициента корреляции.

Критерий Фишера показывает статистическую значимость модели в целом на основе совокупной достоверности всех ее коэффициентов;

Лаговые переменные : – это переменные, относящиеся к предыдущим моментам времени; или -это значения зависим. перемен. за предшествующий период времени.

Лаговые переменные это значение зависимых переменных за предшествующий период времени

Модель в целом статистически значима, если Fрасч > Fтабл.

Модель идентифицирована, если: – число параметров структурной модели равно числу параметров приведён. формы модели.

Модель неидентифицирована, если: – число приведён. коэф . больше числа структурных коэф.

Модель сверхидентифицирована, если: число приведён. коэф. меньше числа структурных коэф

Мультиколлениарность возникает, когда: ошибочное включение в уравнение 2х или более линейно зависимых переменных; 2. две или более объясняющие переменные, в нормальной ситуации слабо коррелированные, становятся в конкретных условиях выборки сильно коррелированными; . в модель включается переменная, сильно коррелирующая с зависимой переменной.

Мультипликативная модель временного ряда имеет вид: – Y=T*S*E

Мультипликативная модель временного ряда строится, если: амплитуда сезонных колебаний возрастает или уменьшается

На основе поквартальных данных…значения 7-1 квартал, 9-2квартал и 11-3квартал …-5

Неправильный выбор функциональной формы или объясняющих переменных называется ошибками спецификации

Несмещённость оценки параметра регрессии, полученной по МНК, означает: – что она характеризуется наименьшей дисперсией.

Одной из проблем которая может возникнуть в многофакторной регрессии и никогда не бывает в парной регрессии, является корреляция между независимыми переменными

От чего зависит количество точек, исключаемых из временного ряда в результате сглаживания: от применяемого метода сглаживания.

Отметьте основные виды ошибок спецификации: отбрасывание значимой переменной; добавление незначимой переменной;

Оценки коэффициентов парной регрессии является несмещённым, если: математические ожидания остатков =0.

Оценки параметров парной линейной регрессии находятся по формуле b= Cov(x;y)/Var(x);a=y¯ bx¯

Оценки параметров регрессии являются несмещенными, если Математическое ожидание остатков равно 0

Оценки параметров регрессии являются состоятельными, если: -увеличивается точность оценки при n, т. е. при увеличении n вероятность оценки от истинного значения параметра стремится к 0.

Оценки парной регрессии явл. эффективными, если: оценка обладают наименьшей дисперсией по сравнению с другими оценками

При наличии гетероскедастичности следует применять: – обобщённый МНК

При проверке значимости одновременно всех параметров используется: -F-тест.

При проверке значимости одновременно всех параметров регрессии используется: F-тест.

Применим ли метод наименьших квадратов для расчетов параметров показательной зависимости применим после ее приведения

Применим ли метод наименьших квадратов(МНК) для расчёта параметров нелинейных моделей? применим после её специального приведения к линейному виду

С помощью какого критерия оценивается значимость коэффициента регрессии T стьюдента

С увеличением числа объясняющих переменных скоррестированный коэффициент детерминации: – увеличивается.

Связь между индексом множественной детерминации R² и скорректированным индексом множественной детерминации Ȓ² есть

Скорректиров. коэф. детерминации: – больше обычного коэф. детерминации

Стандартизованный коэффициент уравнения регрессии Ƀk показывает на сколько % изменится результирующий показатель у при изменении хi на 1%при неизмененном среднем уровне других факторов

Стандартный коэффициент уравнения регрессии: показывает на сколько 1 изменится y при изменении фактора xk на 1 при сохранении др.

Суть коэф. детерминации r 2 _xy состоит в следующем: – характеризует долю дисперсии результативного признака y объясняем. регресс., в общей дисперсии результативного признака.

Табличное значение критерия Стьюдента зависит от уровня доверительной вероятности и от числа включённых факторов и от длины исходного ряда.(от принятого уровня значимости и от числа степеней свободы ( n – m -1))

Табличные значения Фишера (F) зависят от доверительной вероятности и от числа включённых факторов и от длины исходного ряда (от доверительной вероятности p и числа степеней свободы дисперсий f1 и f2)..

Уравнение в котором H число эндогенных переменных, D число отсутствующих экзогенных переменных, идентифицируемо если D+1=H

Уравнение в котором H число эндогенных переменных, D число отсутствующих экзогенных переменных, НЕидентифицируемо если D+1 H

Уравнение идентифицировано, если: – D+1=H

Уравнение неидентифицировано, если: – D+1 H

Фиктивные переменные – это: атрибутивные признаки (например, как профессия, пол, образование), которым придали цифровые метки;

Формула t= rxy….используется для проверки существенности коэффициента корреляции

Частный F-критерий: – оценивает значимость уравнения регрессии в целом

Число степеней свободы для факторной суммы квадратов в линейной модели множественной регрессии равно: m;

Что показывает коэффициент наклона – на сколько единиц изменится у, если х изменился на единицу,

Что показывает коэффициент. абсолютного роста на сколько единиц изменится у, если х изменился на единицу

Экзогенная переменная – это независимая переменная или фактор-Х.

Экзогенные переменные — это переменные, которые определяются вне системы и являются независимыми

Экзогенные переменные – это предопределенные переменные, влияющие на зависимые переменные (Эндогенные переменные), но не зависящие от них, обозначаются через х

Эластичность измеряется единица измерения фактора…показателя

Эластичность показывает на сколько % изменится редуктивный показатель y при изменении на 1% фактора xk .

Эндогенные переменные – это: зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через у

Определения

T-отношение (t-критерий) — отношение оценки коэффициента, полученной с помощью МНК, к величине стандартной ошибки оцениваемой величины.

Аддитивная модель временного ряда – это модель, в которой временной ряд представлен как сумма перечисленных компонент.

Критерий Фишера — способ статистической проверки значимости уравнения регрессии, при котором расчетное (фактическое) значение F-отношения сравнивается с его критическим (теоретическим) значением.

Линейная регрессия — это связь (регрессия), которая представлена уравнением прямой линии и выражает простейшую линейную зависимость.

Метод инструментальных переменных — это разновидность МНК. Используется для оценки параметров моделей, описываемых несколькими уравнениями. Главное свойство — частичная замена непригодной объясняющей переменной на такую переменную, которая некоррелированна со случайным членом. Эта замещающая переменная называется инструментальной и приводит к получению состоятельных оценок параметров.

Метод наименьших квадратов (МНК) — способ приближенного нахождения (оценивания) неизвестных коэффициентов (параметров) регрессии. Этот метод основан на требовании минимизации суммы квадратов отклонений значений результата, рассчитанных по уравнению регрессии, и истинных (наблюденных) значений результата.

Множественная линейная регрессия — это множественная регрессия, представляющая линейную связь по каждому фактору.

Множественная регрессия — регрессия с двумя и более факторными переменными.

Модель идентифицируемая — модель, в которой все структурные коэффициенты однозначно определяются по коэффициентам приведенной формы модели.

Модель рекурсивных уравнений — модель, которая содержит зависимые переменные (результативные) одних уравнений в роли фактора, оказываясь в правой части других уравнений.

Мультипликативная модель – модель, в которой временной ряд представлен как произведение перечисленных компонент.

Несмещенная оценка — оценка, среднее которой равно самой оцениваемой величине.

Нулевая гипотеза — предположение о том, что результат не зависит от фактора (коэффициент регрессии равен нулю).

Обобщенный метод наименьших квадратов (ОМНК) — метод, который не требует постоянства дисперсии (гомоскедастичности) остатков, но предполагает пропорциональность остатков общему множителю (дисперсии). Таким образом, это взвешенный МНК.

Объясненная дисперсия — показатель вариации результата, обусловленной регрессией.

Объясняемая (результативная) переменная — переменная, которая статистически зависит от факторной переменной, или объясняющей (регрессора).

Остаточная дисперсия — необъясненная дисперсия, которая показывает вариацию результата под влиянием всех прочих факторов, неучтенных регрессией.

Предопределенные переменные — это экзогенные переменные системы и лаговые эндогенные переменные системы.

Приведенная форма системы — форма, которая, в отличие от структурной, уже содержит одни только линейно зависящие от экзогенных переменных эндогенные переменные. Внешне ничем не отличается от системы независимых уравнений.

Расчетное значение F-отношения — значение, которое получают делением объясненной дисперсии на 1 степень свободы на остаточную дисперсию на 1 степень свободы.

Регрессия (зависимость) — это усредненная (сглаженная), т.е. свободная от случайных мелкомасштабных колебаний (флуктуаций), квазидетерминированная связь между объясняемой переменной (переменными) и объясняющей переменной (переменными). Эта связь выражается формулами, которые характеризуют функциональную зависимость и не содержат явно стохастических (случайных) переменных, которые свое влияние теперь оказывают как результирующее воздействие, принимающее вид чисто функциональной зависимости.

Регрессор (объясняющая переменная, факторная переменная) — это независимая переменная, статистически связанная с результирующей переменной. Характер этой связи и влияние изменения (вариации) регрессора на результат исследуются в эконометрике.

Система взаимосвязанных уравнений — это система одновременных или взаимозависимых уравнений. В ней одни и те же переменные выступают одновременно как зависимые в одних уравнениях и в то же время независимые в других. Это структурная форма системы уравнений. К ней неприменим МНК.

Система внешне не связанных между собой уравнений — система, которая характеризуется наличием одних только корреляций между остатками (ошибками) в разных уравнениях системы.

Случайный остаток (отклонение) — это чисто случайный процесс в виде мелкомасштабных колебаний, не содержащий уже детерминированной компоненты, которая имеется в регрессии.

Состоятельные оценки — оценки, которые позволяют эффективно применять доверительные интервалы, когда вероятность получения оценки на заданном расстоянии от истинного значения параметра становится близка к 1, а точность самих оценок увеличивается с ростом объема выборки.

Спецификация модели — определение существенных факторов и выявление мультиколлинеарности.

Стандартная ошибка — среднеквадратичное (стандартное) отклонение. Оно связано со средней ошибкой и коэффициентом доверия.

Степени свободы — это величины, характеризующие число независимых параметров и необходимые для нахождения по таблицам распределений их критических значений.

Тренд — основная тенденция развития, плавная устойчивая закономерность изменения уровней ряда.

Уровень значимости — величина, показывающая, какова вероятность ошибочного вывода при проверке статистической гипотезы по статистическому критерию.

Фиктивные переменные — это переменные, которые отражают сезонные компоненты ряда для какого-либо одного периода.

Эконометрическая модель — это уравнение или система уравнений, особым образом представляющие зависимость (зависимости) между результатом и факторами. В основе эконометрической модели лежит разбиение сложной и малопонятной зависимости между результатом и факторами на сумму двух следующих компонентов: регрессию (регрессионная компонента) и случайный (флуктуационный) остаток. Другой класс эконометрических моделей образует временные ряды.

Эффективность оценки — это свойство оценки обладать наименьшей дисперсией из всех возможных.

Видео:Линейная регрессияСкачать

Тест: Ответы на тест по эконометрике

Тема: Ответы на тест по эконометрике

Аддитивная модель содержит компоненты в виде …

комбинации слагаемых и сомножителей

слагаемых

В линейной регрессии Y=b0+b1X+e параметрами уравнения регрессии являются: (неск)

В правой части приведенной формы системы одновременных уравнений, построенной по перекрестным данным (cross-section data) без учета временных факторов, могут стоять _______ переменные.

экзогенные

В стационарном временном ряде трендовая компонента …

имеет линейную зависимость от времени

отсутствует

имеет нелинейную зависимость от времени

Величина коэффициента детерминации … (неск)

характеризует долю дисперсии зависимой переменной y, объясненную уравнением, в ее общей дисперсии

рассчитывается для оценки качества подбора уравнения регрессии

характеризует долю дисперсии остаточной величины в общей дисперсии зависимой переменной у

оценивает значимость каждого из факторов, включенных в уравнение регрессии

Величина коэффициента регрессии показывает …

среднее изменение фактора при изменении результата на одну единицу измерения

на сколько процентов изменится результат при изменении фактора на 1 %

значение тесноты связи между фактором и результатом

среднее изменение результата при изменении фактора на одну единицу измерения

Величина коэффициента эластичности показывает …

на сколько процентов изменится в среднем результат при изменении фактора на 1%

во сколько раз изменится в среднем результат при изменении фактора в два раза

предельно допустимое изменение варьируемого признака

предельно возможное значение результата

Временным рядом является совокупность значений …

экономического показателя за несколько последовательных моментов (периодов) времени

последовательных моментов (периодов) времени и соответствующих им значений экономического показателя

экономических однотипных объектов по состоянию на определенный момент времени

экономического показателя для однотипных объектов на определенный момент времени

Выберите верные утверждения по поводу структурной формы системы эконометрических уравнений:

каждое уравнение системы может рассматриваться в качестве отдельного уравнения регрессии зависимости одной переменной от группы факторов

система регрессионных уравнений, матрица коэффициентов которых симметрична

эндогенные переменные в одних уравнениях могут выступать в роли независимых переменных в других уравнениях системы

система одновременных уравнений описывает реальное экономическое явление или процесс

Гомоскедастичность остатков подразумевает …

рост дисперсии остатков с увеличением значения фактора

максимальную дисперсию остатков при средних значениях фактора

уменьшение дисперсии остаток с уменьшением значения фактора

одинаковую дисперсию остатков при каждом значении фактора

Диаграмма рассеяния указывает на нелинейную зависимость. В этом случае следует осуществить … (неск)

расчет линейного коэффициента корреляции и использование линейной модели

включение в модель дополнительных факторных признаков

визуальный подбор функциональной зависимости нелинейного характера, соответствующего структуре точечного графика

подбор преобразования переменных, дающего наибольшее по абсолютной величине значение коэффициента парной корреляции

Для линейного уравнения регрессии у = а + bx + e метод наименьших квадратов используется при оценивании параметров…(неск)

Для расчета критического значения распределения Стьюдента служат следующие параметры:

количество зависимых переменных

объем выборки и количество объясняющих переменных

уровень значимости

К классам эконометрических моделей относятся: (неск)

системы нормальных уравнений

корреляционно – регрессионные модели

модели временных рядов

Компонентами временного ряда являются: (неск)

циклическая (сезонная) компонента

тренд

Корреляция подразумевает наличие связи между …

результатом и случайными факторами

переменными

Косвенный метод наименьших квадратов применим для …

неидентифицируемой системы уравнений

неидентифицируемой системы рекурсивных уравнений

любой системы одновременных уравнений

идентифицируемой системы одновременных уравнений

Коэффициент детерминации рассчитывается для оценки качества…

подбора уравнения регрессии

параметров уравнения регрессии

факторов, не включенных в уравнение регрессии

Коэффициент парной корреляции характеризует тесноту ____ связи между _____ переменными.

линейной … двумя

Критические значения критерия Стьюдента определяются по…

двум степеням свободы

трем и более степеням свободы

уровню значимости и одной степени свободы

Метод наименьших квадратов используется для оценивания …

величины коэффициента детерминации

параметров линейной регрессии

величины коэффициента корреляции

средней ошибки аппроксимации

Нелинейным является уравнение регрессии нелинейное относительно входящих в него …

факторов

Несмещенность оценки характеризует …

равенство нулю математического ожидания остатков

наименьшую дисперсию остатков

ее зависимость от объема выборки

увеличение точности ее вычисления с увеличением объема выборки

Обобщенный метод наименьших квадратов применяется в случае…

автокорреляции остатков

Под автокорреляцией уровней временного ряда подразумевается _____ зависимость между последовательными уровнями ряда.

корреляционная

При выполнении предпосылок МНК оценки параметров регрессии обладают свойствами: (неск)

несмещенность

эффективность

Предпосылками МНК являются … (неск)

случайные отклонения коррелируют друг с другом

гетероскедастичность случайных отклонений

случайные отклонения являются независимыми друг от друга

дисперсия случайных отклонений постоянна для всех наблюдений

Примерами фиктивных переменных могут служить: (неск)

пол

образование

Примером нелинейной зависимости экономических показателей является …

зависимость объема продаж от недели реализации, выраженная линейным трендом

линейная зависимость затрат на производство от объема выпуска продукции

линейная зависимость выручки от величины оборотных средств

классическая гиперболическая зависимость спроса от цены

Принципиальные сложности применения систем эконометрических уравнений связаны с ошибками…

однородности выборочной совокупности

спецификации модели

определения случайных воздействий

Система эконометрических уравнений включает в себя следующие переменные:

эндогенные

экзогенные

Способами определения структуры временного ряда являются: (неск)

анализ автокорреляционной функции

расчет коэффициентов корреляции между объясняющими переменными

построение коррелограммы

агрегирование данных за определенный промежуток времени

Среди нелинейных эконометрических моделей рассматривают следующие классы нелинейных уравнений: …

внутренне нелинейные

внутреннее линейные

Структурной формой модели называется система ____ уравнений.

взаимосвязанных

Тенденция временного ряда характеризует совокупность факторов, …

оказывающих сезонное воздействие

оказывающих единовременное влияние

оказывающих долговременное влияние и формирующих общую динамику изучаемого показателя

не оказывающих влияние на уровень ряда

Укажите верные характеристики коэффициента эластичности:

коэффициент эластичности показывает на сколько процентов изменится значение результирующего фактора при изменении на один процент объясняющего фактора

коэффициент эластичности является постоянной величиной для всех видов моделей

коэффициент эластичности показывает на сколько изменится значение результирующего фактора при изменении объясняющего фактора на одну единицу

по значению коэффициента эластичности можно судить о силе связи объясняющего фактора с результирующим

Укажите последовательность этапов оценки параметров нелинейной регрессии Y = a + b*X + c*X².

3 оцениваются параметры регрессии b0, b1, b2

1 выполняется замена переменной X2 на Z

2 задается спецификация модели в виде Y = b₀ + b₁*X +b₂*Z, где b₀ = a; b₁ = b; b₂ =c

4 определяются исходные параметры из тождеств: a = b₀; b = b₁; c = b₂

Укажите последовательность этапов проведения теста Голдфелда-Квандта для парной линейной регрессии.

4 вычисление статистики Фишера

1 упорядочение наблюдений по возрастанию значений объясняющей переменной

3 оценка сумм квадратов отклонений для регрессий по k-первым и k-последним наблюдений

2 оценка регрессий для k-первых и k-последних наблюдений

Укажите справедливые утверждения по поводу критерия Дарбина-Уотсона: (неск)

позволяет проверить гипотезу о наличии автокорреляции первого порядка

изменяется в пределах от 0 до 4

равен 0 в случае отсутствия автокорреляции

применяется для проверки гипотезы о наличии гетероскедастичности остатков

Укажите существующие классы эконометрических систем: (неск)

система нормальных уравнений

система стандартных уравнений

система одновременных уравнений

система независимых уравнений

Укажите требования к факторам, включаемым в модель множественной линейной регрессии: (неск)

между факторами не должна существовать высокая корреляция

факторы должны быть количественно измеримы

факторы должны иметь одинаковую размерность

факторы должны представлять временные ряды

Установите соответствие между названием модели и видом ее уравнения:

3 y = ab x *e;

Установите соответствие между наименованиями элементов уравнения Y=b0+b1X+e и их буквенными обозначениями:

1. параметры регрессии

2. объясняющая переменная

3. объясняемая переменная

4. случайные отклонения

3 Y

4 e

1 b0, b1

2 X

Установите соответствие между эконометрическими терминами и их определениями.

1. автокорреляция уровней временного ряда

2. коэффициент автокорреляции уровней временного ряда

3. автокорреляционная функция

3 последовательность коэффициентов автокорреляции первого, второго и т.д. порядков

4 график зависимости значений автокорреляционной функции от величины лага

1 корреляционная зависимость между последовательными уровнями ряда

2 коэффициент линейной корреляции между последовательными уровнями

Фиктивными переменными в уравнении множественной регрессии являются …

качественные переменные, преобразованные в количественные

комбинации из включенных в уравнение регрессии факторов, повышающие адекватность модели

переменные, представляющие простейшие функции от уже включенных в модель переменных

дополнительные количественные переменные, улучшающие решение

Число степеней свободы общей, факторной и остаточной дисперсий связано …

только с числом единиц совокупности

с числом единиц совокупности и видом уравнения регрессии

характером исследуемых переменных

только с видом уравнения регрессии

Число степеней свободы связано с числом … (неск)

единиц совокупности (количеством наблюдений)

видом уравнения регрессии

раздел экономической теории, связанный с анализом статистической информации

специальный раздел математики, посвященный анализу экономической информации

наука, которая осуществляет качественный анализ взаимосвязей экономических явлений и процессов

наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

Чтобы скачать бесплатно Тесты на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Тесты для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Если Тест, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

Видео:Множественная регрессия в ExcelСкачать

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

Видео:Множественная регрессияСкачать

Эконометрика

Кафедра ___Математика и информатика_________________________

Рейтинговая работа _______________________________________________

(домашняя творческая работа, расчетно-аналитическое задание, реферат, контрольная работа)

по дисциплине ____эконометрика_______________________

Выполнена обучающимся группы __________

(фамилия, имя, отчество)

Москва – 201__ г.

2.3. Рассчитать коэффициенты корреляции и эластичности, коэффициенты эластичности сопоставить с коэффициентами регрессии……………….…….6

2.4. Сделать прогноз на следующий шаг…………………..…………………. 8

1. ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ РЕЙТИНГОВОЙ РАБОТЫ

В соответствии со своим вариантом выбрать исходные данные. Выполнить следующие расчеты:

Построить модель парной линейной регрессии y = a + bx +e.
Изобразить на графике исходные и модельные значения.
Рассчитать коэффициенты корреляции и эластичности, коэффициенты эластичности сопоставить с коэффициентами регрессии.
Сделать прогноз на следующий шаг.

Данные по вариантам: первая строка – значения х, вторая строка – значения у

2. ВЫПОЛНЕНИЕ РЕЙТИНГОВОЙ РАБОТЫ