В какой калибровке уравнения для скалярного и векторного потенциалов независимы

Проблемы, заблуждения и ошибки в электродинамике

Видео:Скалярный и векторный потенциалыСкачать

Часть 2. Заблуждения, порожденные некорректным анализом. Излучение

, , (Исследовательская группа «Анализ»)

Аннотация. В работе рассмотрены явные ошибки в физических теориях. Они порождают негативные следствия в области фундаментальных и прикладных исследований. Ставится проблема исправления этих ошибок в учебниках, лекциях, монографиях.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Введение

«Группа «Анализ» не ставит своей специальной задачей выдвижение каких-либо гипотез. Она четко понимает, что строить новую науку на гнилом основании – авантюризм и безответственность. Главная цель – очистить физические теории от внутренних противоречий, математических, физических и гносеологических ошибок, чтобы создать платформу для новых исследований.» [1].

Теперь мы перейдем к анализу формальных «доказательств», из которых следуют ошибочные или некорректные выводы. В настоящее время эти выводы превратились в предрассудки.

Видео:Останина М.В. - Электродинамика.Лекции.Ч.1 - 3. Векторный и скалярный потенциалы. Уравнение ПуассонаСкачать

1. Обобщение теоремы Пойнтинга

Мы начнем с теоремы Пойнтинга. Общеизвестно, что для ее доказательства Пойнтинг использовал только два из четырех уравнений Максвелла. Он получил закон сохранения для поперечной электромагнитной волны. С тех пор вектором Пойнтинга как шаблоном пользуются во всех случаях даже тогда, когда он принципиально неприменим и ведет к абсурдным результатам. Примеры можно найти в работе [2].

Уравнения Максвелла в калибровке Лоренца имеют следующий вид

(1.1)

Из уравнений следует, что должны существовать хотя бы продольные волны скалярного потенциала. Для них в доказательстве Пойнтинга места не нашлось. Положение усугубилось тем, что продольные волны до сих пор не были обнаружены экспериментально.

Нам удалось математически строго доказать работе [3] (Глава 7), что для уравнений Максвелла в калибровке Лоренца имеет место обобщенный закон сохранения энергии-импульса. Он вытекает из тензора энергии-импульса для электромагнитных волн. Попутно заметим, что «тензор энергии-импульса», который встречается в работе [4] является фальсификацией. Из дивергенции этого тензора не следуют законы сохранения, а «выводится» одно из уравнений Максвелла.

Итак, выпишем из работы [3] (Глава 7) обобщенные выражения для законов сохранения. Они имеют стандартный вид для свободного пространства

1. Закон сохранения плотности потока S электромагнитного поля волны

(1.2)

2. Закон сохранения плотности энергии w электромагнитного поля волны

(1.3)

Для наглядности мы представим векторный потенциал и плотность тока в виде суммы вихревой и безвихревой компонент

(1.4)

Иными словами, мы разделили векторное уравнение на два независимых волновых уравнения. Таким образом, мы имеем дело фактически с тремя волновыми уравнениями: волновым уравнением для вихревой составляющей векторного потенциала, волновым уравнением для безвихревой составляющей векторного потенциала и волновым уравнением для скалярного потенциала.

В соответствии с этим мы будем иметь три закона сохранения для соответствующих плотностей энергии и три закона сохранения для соответствующих плотностей потоков вида (1.2) и (1.3).

Поперечные волны векторного потенциала

Продольные волны векторного потенциала

Продольные волны скалярного потенциала

Из полученных соотношений следуют весьма интересные выводы.

1.Во-первых, вопреки сложившимся представлениям в общем случае уравнения Максвелла в калибровке Лоренца описывают три различных вида потоков. Первый поток энергии есть известный поток поперечных электромагнитных волн, описываемый вектором Пойнтинга. Его плотность равна . Второй поток – поток продольных электрических волн векторного потенциала А. Его плотность равна . Третий поток – поток продольных волн, образованный скалярным потенциалом f с плотностью потока .

2.Во вторых, плотность энергии и плотность потоков S1 и S2 , образованных векторным потенциалом А, положительны, а плотность энергии и плотность потока S3 , созданного скалярным потенциалом f, отрицательны.

Итак, мы выявили первое заблуждение. Вопреки сложившемуся мнению уравнения Максвелла могут описывать продольные волны скалярного и векторного потенциалов.

Видео:Аналитическая геометрия, 2 урок, Скалярное произведениеСкачать

2. Безынерциальные заряды и токи

Поскольку экспериментально продольные волны до настоящего времени не были обнаружены, мы имеем право предположить, что продольные волны скалярного и векторного потенциалов взаимно уничтожают друг друга. Иными словами, величины S2 + S3 и w2 + w3 при очень больших расстояниях должны убывать быстрее, чем r-2.

В работе [3] (Глава 7) показано, что взаимное уничтожение потоков продольных волн возможно в том и только в том случае, если плотности зарядов и плотности токов удовлетворяют однородному волновому уравнению

(2.1)

Поскольку плотность пространственного заряда обуславливает как вихревую, так и безвихревую части суммарной плотности тока, выражение (2.1) можно распространить на суммарную плотность тока j.

Выражение (2.1) не согласуется с формулой для тока (1.1) j = vr. Из выражения (2.1) следует, что мы имеем дело с безынерциальными зарядами, которые движутся (например, вдоль проводника) со скоростью света j = cr. Только безынерциальные токи способны обеспечить отсутствие излучения продольных волн диполем Герца.

Нетрудно показать, используя потенциалы Льенара-Виехерта, что зяряд, совершающий возвратно-поступательное движение вблизи положения равновесия при малых линейных скоростях перемещения (v ≠ c), создает на большом расстоянии от себя изотропное излучение в виде суммы продольных и поперечных волн [5].

Безынерциальные заряды отнюдь не гипотеза. Специалисты по антенно-фидерным устройствам сталкиваются с ними постоянно. Действительно, поверхностные токи в волноводах, коаксиальных линиях (без диэлектриков) распространяются со скоростью света в вакууме. Попытки описать эти токи и заряды, опираясь на электронную проводимость, ведут к противоречию с опытом. Во-первых, при таком описании мы должны считать инерциальную массу носителей равной нулю. Во вторых, при описании (например, распространения переменного тока в бесконечной длинной линии) неизбежно появляется постоянная составляющая магнитного поля, которая экспериментально не обнаруживается.

Все это ведет к мысли, что безынерциальные заряды могут быть как положительными, так и отрицательными. Такой вид проводимости в проводниках существует наряду (параллельно) с электронной, ионной и дырочной проводимостями. Природу этих зарядов еще предстоит установить.

Интересный эксперимент, подтверждающий волновой характер безинерциальных зарядов, был проделан Авраменко схема эксперимента показана на рис. 1. Им было отмечено интересное свойство этого тока. Безинерциальные заряды как будто «не чувствовуют» сопротивления.

Рис. 1 С – уединенные емкости.

На рис. 1 показана упрощенная схема опыта. В первом случае микроамперметр показывал ток I0. Во втором случае (Рис. 1b) замена диода короткозамыкающей перемычкой должна была приводить к исчезновению тока через прибор. Однако ток протекал, и его величина была ровно в два раза меньше, чем в предыдущем случае. На Рис.1 показаны направления прохождения токов при различных фазах переменного напряжения, иллюстрирующие причину уменьшения тока в 2 раза.

Теперь можно сказать, что выявлен второй предрассудок. Оказывается, что за излучение поперечных электромагнитных волн отвечают безинерциальные заряды и токи, о которых нет упоминания в физической научной и учебной литературе.

Видео:Сравнение скалярного и векторного произведений векторов (видео 16) | Магнетизм | ФизикаСкачать

3. Загадка калибровочной инвариантности

Существуют доказательства того, что при заданных начальных и граничных условиях уравнения Максвелла имеют единственное решение. Это позволяет выразить электрические и магнитные поля через потенциалы, чтобы упростить постановку задач, формулировку начальных и граничных условий. В настоящее время широко используются в основном две калибровки (кулоновская калибровка и калибровка Лоренца). Считается, что эти калибровки эквивалентны. Тем не менее, в физической литературе постоянно обсуждается проблема эквивалентности этих калибровок [6], [7], [8] и др.

Рассмотрим таблицу, в которой приведены основные формулы.

Система уравнений Максвелла

Выражения для полей Е и Н

Критики принципа эквивалентности калибровок делают следующие справедливые замечания, вытекающие из сопоставления уравнений для этих калибровок.

1. Все потенциалы в калибровке Лоренца имеют запаздывающий характер. В кулоновской калибровке скалярный потенциал f’описываемый уравнением Пуассона, является мгновенно действующим.

2. В общем случае калибровка Лоренца может описывать излучение продольных волн. В то же время, кулоновская калибровка описывает только поперечные волны вихревого векторного потенциала.

Этих аргументов достаточно, чтобы подвергнуть сомнению справедливость формального (символьного) доказательства эквивалентности калибровок. Формальный подход не учитывает функционального различия (мгновенное дальнодействие, запаздывание) преобразуемых потенциалов.

Калибровочную инвариантность нельзя рассматривать в отрыве от условия поперечного характера электромагнитных волн. Это условие накладывает жесткие рамки на источники электромагнитного излучения (заряды и токи).

Как мы установили, заряды в калибровке Лоренца при этом условии должны иметь запаздывающий характер, т. е. зависеть от r – ct, т. е. они должны распространяться вдоль проводников со скоростью света. С учетом этого условия Таблица 1 примет следующий вид

Система уравнений Максвелла

Выражения для полей Е и Н

Источники формируют электромагнитные поля. От них зависит характер излученных волн и это принципиально важно учитывать. Только при таких источниках и при такой связи потенциалов имеет место эквивалентность кулоновской калибровки и калибровки Лоренца (а) и обеспечивается отсутствие продольных электромагнитных волн в решениях уравнений Максвелла (б). Любые другие варианты требуют дополнительного исследования.

Из анализа следует интересный и важный вывод: инерциальные заряды (электроны, позитроны, протоны и т. д.) не излучают электромагнитные волны при ускоренном движении! Они «выпали» из уравнений. Более подробно об этом в [9]. Это позволяет отсечь еще один предрассудок, касающийся излучения волн ускоренными инерциальными зарядами.

Видео:СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

4. Неполнота уравнений Максвелла

Как мы убедились, калибровка Лоренца и требование отсутствия в решениях продольных волн исключает описание полей инерциальных зарядов. Тем не менее, такие заряды существуют и их описание необходимо.

Проблема описания полей инерциальных зарядов была нами решена в дифференциальной форме [10] еще в 1974 г. В более поздних работах была разработана интегральная форма описания полей зарядов, сформулированы законы сохранения для этих полей и описано взаимодействие этих зарядов [3] (Главы 3, 4, 5, 6). Эти вопросы были решены в рамках нерелятивистских представлений. В следующей части мы рассмотрим эти вопросы.

Но прежде мы рассмотрим возможность решения проблемы электромагнитной массы в рамках запаздывающих потенциалов. Хотя мы заранее предвидели негативный результат, мы провели исследования, чтобы очертить возникающие при этом проблемы.

Обратимся к результатам работы [2]. Там рассмотрены два варианта модели точечного заряда. Заметим, что инерциальная масса покоя заряженной частицы отлична от нуля, а сама частица может иметь любую скорость в рамках квазистатических представлений.

Первый вариант. Скалярное поле заряда описывается выражением (решение волнового уравнения для скалярного потенциала)

(4.1)

где

Анализ, опирающийся на изложенные в параграфе 1 (Обобщение теоремы Пойнтинга) законы сохранения, привел к странным результатам.

Электромагнитная масса, определяемая из энергии поля скалярного потенциала имеет отрицательный знак! (4.2) В то же время, кинетическая энергия, этой массы имеет положительный знак!

Ситуация с точки зрения классических представлений весьма абсурдная. Возможно, частицы с такими необычными свойствами встречаются в природе, но пока о частицах с такими свойствами в современной научной литературе мы не обнаружили. Этот вариант не может быть использован для описания свойств заряженных частиц (например, электронов).

Второй вариант. Он опирается на использование уравнения непрерывности для скалярного потенциала, описываемого волновым уравнением

(4.3)

Поскольку этот вопрос не обсуждался в учебниках по математической физике, мы рассмотрим его подробнее.

Уравнение непрерывности для векторного потенциала позволяет преобразовать волновое уравнение для скалярного потенциала к виду

(4.4)

Итак, мы преобразовали уравнение гиперболического типа в уравнение эллиптического типа, волновое уравнение в уравнение Пуассона. Теперь начальные условия нам не нужны. Решением этого уравнения будет

(4.5)

Этот же результат можно получить, используя преобразование Лоренца. Факт интересен с той точки зрения, что формально выражение (4.5) описывает мгновенное действие на расстоянии (уравнение Пуассона)! С другой стороны, выражение (4.5) является также решением волнового уравнения (вырожденное решение).

По этой причине мы можем формально выражение (4.5) представить как сумму опережающего и запаздывающего потенциалов [2].

Можно показать [2], что для такого потенциала существует свой закон сохранения энергии-импульса

, (4.6)

где — плотность потока и плотность энергии поля заряда.

Плотность потока Su есть плотность потока вектора Умова. Она, в отличие от вектора Пойнтинга, описывает конвективный перенос энергии поля зарядом со скоростью v зарядом. Здесь мы устраняем путаницу между векторами, которая существует уже не одно десятилетие.

Соотношения (4.6) имеют форму, близкую к классической (наличие релятивистского множителя). Здесь нарушений логики нет. Однако описанный механизм возникновения инерции имеет существенные недостатки.

1. Во-первых, в потенциал поля заряда входит опережающий компонент. С точки зрения причинности это серьезный дефект описания.

2. Во вторых, плотность энергии и плотность потока сохраняют отрицательный знак в соответствии с выражением (4.2).

Таким образом, решение проблемы электромагнитной массы в рамках волнового характера потенциала невозможно. Это определяет неполноту уравнений Максвелла. Возможно, что в калибровке Лоренца «скрыта» еще одна система уравнений

(4.7)

Индексом «0» мы обозначили мгновенно действующие потенциалы. Но это предмет обсуждения следующей части.

Итак, мы уничтожаем еще одно заблуждение. Мы установили, что: «Поля заряженных частиц и электромагнитные волны суть разные виды материи, обладающие каждый своими уникальными свойствами».

Видео:Соколов В.А. - Электродинамика.Часть 2.Лекции - 3. Уравнения для потенциаловСкачать

5. Так кто же отвечает за Российскую Науку?

Ошибки и предрассудки, тиражируясь в лекциях, учебниках и исследованиях, не способствуют нормальному развитию науки и воспитанию будущих ученых. Эти «погрешности науки» необходимо искоренять. Есть много организаций, которые имеют отношение к высшему образованию и науке.

Минобрнауки, возглавляемое Фурсенко. Можно обратиться туда. Но какой смысл? Судя по реформам образования, в этом министерстве нет специалистов ни по науке, ни педагогике («кухарки»!). Недавно Чубайс назвал Фурсенко крупным реформатором. Сколько же нужно сделать нехорошего для России, чтобы заслужить такую похвалу?

Есть РАН с Осиповым. Многочисленные обращения профессоров по поводу современного состояния физики (без ответов от РАН) не оставляют сомнения, что Осипов мирно дремлет в Президентском кресле. Вместе с ним богатырским сном спит Отделение Физических Наук. Их мирный сон охраняет Комиссия по борьбе с лженаукой и фальсификацией научных исследований.

Обращение в Комиссию по борьбе с лженаукой и фальсификацией научных исследований тоже не имеет перспектив. Уж больно «топорным» критерием научности пользуется эта Комиссия: «ЕСТЬ МИРОВАЯ НАУКА, А ВСЕ, ЧТО НЕ ВПИСЫВАЕТСЯ В ЕЕ КРИТЕРИИ – ЭТО ЛЖЕНАУКА» [8]. Мы обнаружили ошибки в научных теориях современной физики. Выводы «противоречат твердо установленным научным фактам» (по Гинзбургу), т. е. «не вписываются в кругляковские критерии научности». Нам заранее уготовлена участь быть обвиненными в «невежестве», «некомпетентности», «шарлатанстве» и т. д. Однако сейчас кличка «альтернативщик» уже утратила свой оскорбительный смысл. Напротив, она отражает нетерпимость исследователя-альтернативщика к ошибкам и предрассудкам в современной физике. Не без оснований Грызлов назвал эту Комиссию «гнездом мракобесия». Быть может Единая Россия здесь поможет?

Обратились в Приемную Грызлова. Нам обещали дать ответ через месяц. Год ждем. Как при игре «домино» и здесь выпадает фишка «пусто-пусто». Уж очень странная эта Партия «Единая Россия», много обещающая.

Есть пословица: «У семи нянек дитя без глазу». Это верно, если нянек интересует не «дитя», а ученые степени, научные звания, хорошие зарплаты и высокие должности. Им ли до «дитяти»? Все как в сказке: Докторов наук тьма, а Ученых нема!

Так и остался наш вопрос без ответа: Кто же все-таки отвечает за Российскую Науку?

В последующих Частях мы продолжим публикацию анализа ошибок и предрассудков в электродинамике. Мы рассмотрим вопросы, касающиеся электромагнитной массы инерциальных зарядов и квазистатических явлений.

1. Исследовательская группа АНАЛИЗ http://n-t/ru/ac/iga/

2. , , Кулигина и инерция http://www. /texsts/rus/stat/st3637.htm

3. , , Кулигина классической электродинамики и теории относительности http:///tp/ns/ak. htm

4. , Лифшиц поля. Физматгиз., М. 1961.

5. , , Кулигина ляпы в электродинамике http://www. /rus/catalog/pages/8802.html

6. Onoochin V On non-equivalence of Lorentz and Coulomb gauges within classical electrodynamics Ann.Fond. Louis Broglie 27 163–84 (2002)

7. Engelhardt W Gauge invariance in classical electrodynamics Ann. Fond. Louis Broglie 30 157–78

8. Arfken G B and Weber H J 1995 Mathematical Methods for Physicists (New York: Academic) (2005)

9. . Противоречия в современной концепции излучения заряженных частиц и строения атома. //Проблемы пространства, времени, тяготения. (IV Международная конференция 16-1.09.1996). ПОЛИТЕХНИКА, С.-П., 1997.

10. , ВНИИГПЭ. Заявка на открытие «Электромагнитная масса» 32-ОТ- 8457, 1974

Видео:Скалярное произведение векторов. 9 класс.Скачать

Векторный потенциал и его связь с вектором индукции магнитного поля

Вы будете перенаправлены на Автор24

Видео:Линал | Лекция 2. Скалярное, векторное, смешанное, двойное векторное произведения.Скачать

Определение векторного потенциала

Одно из основных уравнений магнитостатики имеет вид:

Решение этого уравнения может быть определено как:

где вектор $overrightarrow$ называют векторным потенциалом магнитного поля. Из векторного анализа хорошо известно тождество:

Видео:Оператор набла (оператор Гамильтона) и оператор ЛапласаСкачать

Многозначность векторного потенциала

Поле, в котором известен вектор индукции ($overrightarrow$) может быть описано несколькими векторными потенциалами. Покажем, что если потенциал $overrightarrow$описывает поле с индукцией $overrightarrow$, то и другой потенциал $overrightarrow$, в виде:

при любом $varkappa$, описывает то же самое поле. Проведем операцию rot уравнения (4), получим:

так как $rotleft(gradvarkappa right)equiv 0.$

Многозначность векторного потенциала магнитного поля эквивалентна неоднозначности скалярного потенциала электростатического поля. Разница состоит в том, что потенциал в электростатике определяется с точностью до произвольной постоянной, тогда как векторный потенциал магнитостатического поля, определятся с точностью до произвольной функции определённого класса. Произвольность в выборе векторного потенциала показывает, что векторный потенциал имеет вспомогательное значение. Он не может быть измерен в эксперименте.

Видео:Скалярные и векторные поля. ТемаСкачать

Калибровка векторного потенциала

В магнитостатике в качестве калибровочного условия для векторного потенциала используют уравнение:

Уравнение (6) называют условием калибровки потенциала.

Видео:О диаграмме Смитта и калибровке векторных рефлектометров.Скачать

Уравнение для векторного потенциала

Запишем теорему о циркуляции вектора $overrightarrow$ в дифференциальной форме:

где $overrightarrow$ — вектор плотности тока, $_0$ — магнитная постоянная. Подставим (2) в уравнение циркуляции (7), получим:

В координатном представлении уравнение (10) запишется в форме:

В системе уравнений (11) мы получили, что каждая компонента векторного потенциала подчиняется уравнению Пуассона. Следовательно, можно предположить, что решение уравнений (11) можно записать в виде:

где $r$ — радиус вектор, который проведен из элемента тока в точку наблюдения. В векторной форме (12) запишем как:

Готовые работы на аналогичную тему

Для тока в прямолинейном проводнике (линейного тока), можно записать, что векторный потенциал равен:

где $L_i$- контуры токов, $I_i$- силы токов в контурах.

Если найден векторный потенциал, то используя его определение можно отыскать соответствующую ему индукцию магнитного поля. Введение векторного потенциала существенно облегчает изучение магнитного поля постоянных токов.

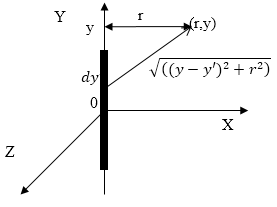
Задание: Найдите вектор-потенциал магнитного поля, которое создается прямолинейным током проводника длинны L. Сила тока в проводнике I.

Пусть начало координат находится в середине, рассматриваемого участка с током (рис.1).

Магнитное поле прямолинейного проводника с током обладает цилиндрической симметрией, следовательно. Координаты точки в данной плоскости характеризуются расстоянием r от оси Y и координатой y. В качестве основы для решения задачи используем выражение:

Из (1.1) следует, что не равна нулю только компонента $A_yne 0$. ($A_x=0_z=0$) так как ток течет только по оси Y. В таком случае запишем:

Для бесконечно длинного проводника векторный магнитный потенциал равен:

Задание: Используя результат решения задачи «Пример 1». Найдите индукцию магнитного поля, которое создается прямолинейным током проводника длинны L. Сила тока в проводнике I. (рис.1).

Из симметрии магнитного поля данного проводника с током индукцию достаточно вычислить в точках плоскости XY. Будем вычислять ее по формуле:

где из предыдущей задачи имеем:

Удобнее индукцию, опять таки из соображений симметрии поля, записать в цилиндрических координатах. При этом будем иметь, что не равна нулю только проекция $B_$, где $varphi $ — угол цилиндрической системы координат. При этом можно записать, что:

На рис. 1 на плоскости XY $компонента B_$ направлена перпендикулярно плоскости в против оси Z. Подставим (2.2) в (2.3), получим:

Для бесконечного прямолинейного проводника имеем:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 09.02.2022

🎥 Видео

Лекция 18. Скалярное произведение векторов и его свойства.Скачать

Векторный метод в стереометрии. Задача 14 профильный ЕГЭСкачать

Скалярное и векторное поля. Определения и отличия.Скачать

Лекция 233 оператор набла. Уравнения МаксвеллаСкачать

Линейные комбинации, span и базисные вектора | Сущность Линейной Алгебры, глава 2Скачать

Суть векторного регулированияСкачать

Геометрический смысл скалярного произведения. ТемаСкачать

Скалярные произведения и дуальность | Сущность Линейной Алгебры, глава 7Скачать