- Конспект урока по алгебре 7 класс на тему «Линейное уравнение с одной переменной» план-конспект урока по алгебре (7 класс)
- Скачать:
- Предварительный просмотр:
- «Линейное уравнение с одной переменной». 7-й класс
- Ход урока
- I. Организационный момент.
- II. Актуализация знаний.
- III. Изучение нового материала.
- IV. Первичное закрепление изученного материала.
- V. Домашнее задание
- VI. Итог урока.
- 📽️ Видео
Конспект урока
Решение линейных уравнений с одним неизвестным
Перечень рассматриваемых вопросов:
• Решение линейных уравнений.
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
Корень уравнения – это число, при подстановке которого в уравнение получается верное равенство.
Переменная – символ, используемый для представления величины, которая может принимать любое из ряда значений.
Свободный член – член уравнения, не содержащий неизвестного.
Решить уравнение – значит найти все его корни или установить, что их нет.
Преобразование – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному.
Основная литература:
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Давайте вспомним, что называется корнем уравнения?
Корнем уравнения называют, такое значение переменной, при которой уравнение преобразуется в верное числовое равенство.
А что же означает решить уравнение?
Решить уравнение означает найти все его корни или доказать, что корней нет.
Давайте попробуем сформулировать теперь, как решать линейные уравнения и подумаем, а какие у нас могут быть случаи?
Решение линейного уравнения – это приведение его путем тождественных преобразований к стандартному виду.
Давайте решим уравнение:
Следовательно, уравнение не имеет корней.
А теперь давайте решим другое уравнение:
Попробуем решить уравнение:
При любом значении переменной, уравнение принимает вид верного равенства:
0 = 0, следовательно, уравнение имеет бесконечное множество корней.
Отсюда можно сделать вывод, что возможные варианты решения уравнения, зависят от того, какие значения принимает свободный член и коэффициент при переменной.
При решении уравнения вида возможны следующие три случая:
Замечательно, а теперь узнаем, можно ли проверить, является число корнем уравнения не решая его?
Да, конечно можно. Для этого нужно подставить в уравнение вместо переменной это число, если после упрощения, мы получаем верное равенство, то данное число будет являться корнем уравнения.
Давайте проверим, так ли это. Узнаем, является ли число
Замечательно. А теперь давайте попробуем порешать линейные уравнения первой степени.
является корнем уравнения.
уравнение к стандартному виду. Слагаемые, зависящие от икс, перенесём в левую часть уравнения, числа – в правую, изменяя их знаки на противоположные.
Разбор заданий тренировочного модуля.
содержащие переменной в правую часть, меняя знак на противоположный;
слагаемые, содержащие переменную в левую часть, не содержащие переменной, в правую часть, меняя знак на противоположный;
Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Конспект урока по алгебре 7 класс на тему «Линейное уравнение с одной переменной»
план-конспект урока по алгебре (7 класс)
Конспект урока по алгебре 7 класс на тему «Линейное уравнение с одной переменной» Тип урока : урок изучения первичного закрепления новых знаний.
Цели: — общеобразовательные: ВВести определение линейного уравнения с одной переменной; отработать вычислительные навыки решения линейных уроавнений с одним неизвестным сведением его к линейному уравнению с помощью свойств равносильности.
— развивающие: способствовать формированию умений применять приемы обобщения, сравнения, развития мышления и памяти;
— воспитательные: содействовать формированию культуры общения.
Видео:Алгебра 7 Линейное уравнение с одной переменнойСкачать

Скачать:
| Вложение | Размер |
|---|---|
| Урок на тему «Линейное уравнение с одной переменной» | 2.58 МБ |
Видео:Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Предварительный просмотр:
Тема урока: Линейное уравнение с одной переменной
Тип урока : урок изучения и первичного закрепления новых знаний
- Общеобразовательные : ввести определение линейного уравнения с одной переменной; отработать вычислительные навыки решения уравнения с одним неизвестным сведением его к линейному уравнению с помощью свойств равносильности; выяснить, сколько корней может иметь линейное уравнение; проверить усвоение знаний и умений;
— развивающие: способствовать формированию умений применять приемы обобщения, сравнения, развития мышления и памяти;
научить учащегося решать линейные уравнения, используя свойства равносильности уравнений.
— воспитательные: содействовать формирование культуры общения, воспитание чувства взаимопомощи, активности, организованности, ответственности, волевых качеств, умению работать в группе.
Оборудование : Компьютер, программа Power Point
- Организационный момент. (слайд 1,2)
Поприветствовать учащегося, проверить его готовность к уроку, объявить тему урока и цель урока.
Первое условие, которое надлежит выполнять в
математике, — это быть точным,
второе — быть ясным и, насколько можно, простым.
Природа говорит языком
этого языка — круги,
треугольники и иные
- Проверка домашнего задания.
Проверка домашней работы вместе с учащимся при помощи демонстрации экрана.
1)Фронтальный опрос. (Слайд3)
— Определение линейного уравнения с одной переменной.
— Когда линейное уравнение с одной переменной может иметь один корень, два корня, ни одного корня?
— Какие тождественные преобразования помогают сделать замену уравнения равносильным ему??
— Какие свойства уравнений вы знаете?
— Что значит «решить уравнение»?
-Что называется корнем уравнения?
2)Устная работа. (Слайд 4)
а) 5х=-60; 6х=-50; -1,5х=6; 0,7х=0.
б) 14-у=19-11у; 0,5а+11=4-3а; 1,2n+1=1-n; -0,7х+2=65.
в) Является ли корнем уравнения х 2 -1=0 число: а)-2; б)-1; в)0 ; г) 1; д)2 ?
г) Равносильны ли уравнения(устно):
д)Решите уравнения (устно):
IхI=11; IхI=0; IхI=-5
5.Изучение нового материала. ( Слайд5)
Мухаммед ибн Муса аль – Хорезми
Уравнение и его свойства
(повторение теоретического материала)
Уравнение – это равенство, содержащее одну или несколько переменных.
Линейное уравнение с одной переменной
- если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному.
- если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Линейное уравнение с одной переменной. Правила.
Уравнением с одной переменной, называется равенство, содержащее только одну переменную.
Корнем (или решением) уравнения называется такое значение переменной, при котором уравнение превращается в верное числовое равенство.
Найти все корни уравнения или доказать, что их нет – это значит решить уравнение.
Свойство 1 . При переносе слагаемого из одной части уравнения в другую с противоположным знаком, получается уравнение с теми же корнями.
x – 3 = 6 ⇒ x = 6 + 3 ⇒ x = 9 .
Свойство 2 . При умножении или делении обеих частей уравнения на одно и то же число, отличное от нуля, мы получим уравнение с теми же корнями (решениями).
3x = 6 ⇒ 3x : 3 = 6 : 3 ⇒ x = 2 .
Уравнение вида ax = b называется линейным. Например:
2. 3x – 3 = 9 ; 3x = 9 + 3 ; 3x = 12 ( ax = b ) .
Принято: цифры в алгебраических выражениях заменять
первыми буквами латинского алфавита — a, b, c, …,
а переменные обозначать последними — x, y, z.
a ≠ 0 b — любое значение ax = b имеет один корень x = b : a .
a = 0 b ≠ 0 ax = b не имеет корней .
a = 0 b = 0 ax = b имеет бесконечно много корней .
3x = 3 один корень x = 3 : 3 x = 1 .
0 • x = 5 корней нет .
0 • x = 0 бесконечно много корней x — любое число . . ( Слайд №7 )
Рассмотрим алгоритм решения линейных уравнений с одной переменной:
Работа по группам
8(2х – 1) – 5(3х + 0,8) = х-4
-(18 + 4х)х = 76 – 2х(2х – 1)
- 12 – х) – (3х + 4) = – х – 1
- — 4 + (2х – (4х+1))+ х = — 5 — х
- 8х + 40 = 100 + 2х
- 61 – (3х – 51) = 1
- 3,5 – 3х = 2,3 + х
- Закрепление изученного материала.
Поле чудес (слайд 12)
- 8х + 40 = 100 + 2х 10 Х
- 61 – (3х – 51) = 1 3 О
- 3,5 – 3х = 2,3 + х 0,3 Р
- (12 – х) – (3х + 4) = – х – 1 3 Е
- — 4 + (2х – (4х+1))+ х = — 5 — х л/ч З
- 8(2х – 1) – 5(3х + 0,8) = х-4 к/н М
- -(18 + 4х)х = 76 – 2х(2х – 1) -3 4/5 И
Все умеем мы считать
Раз, два, три, четыре, пять,
Все умеем мы считать. (Сгибание и разгибание рук вверх.)
До пяти мы все считаем,
С силой гири поднимаем.
Сколько раз ударю в бубен,
Столько раз дрова разрубим. (Наклоны вперед, руки в «замок», резко вниз.)
Сколько точек будет в круге,
Столько раз поднимем руки. (Расслабленное поднимание и опускание рук.)
Наклонитесь столько раз,
Сколько форточек у нас. (Наклоны в стороны, руки на пояс.)
Сколько клеток до черты,
Столько раз подпрыгни ты. (Прыжки на месте.)
Мы теперь — канатоходцы,
Сколько можем простоять. (Ходьба на месте, руки в стороны. Ступни ног на одной линии, одна впереди другой, руки в стороны.)
а)Найди ошибку (слайд13)
(3х + 7) * 2 – 3 = 17
Решите уравнения: ( по вариантам)
-5х – 1 = 2х + 2 -9х + 5 = 6х – 4
1)1/3 2) -3/7 3) -1/3 4)3/7 1)1/3 2)0,3 3)3/5 4)-3
-2(5 – х) = 1,5х + 0,5(х + 4) 3(2 – х)=(6 – 5х)+2х
1)-3 2)-4 3)н/к 4)л/ч 1)1 2)0 3)н/к 4)л/ч
1) 3 и -3 2) -3 3) 3 4) н/к 1)11 2) -11 3) н/к 4) 11 и -11
8.Домашнее задание ( слайд16 )
9. Подведение итогов:
Алгоритм решения уравнения:
-Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.
-Привести подобные члены.
-Разделить обе части уравнения на коэффициент при неизвестном.
Вывод : Ребята, сегодня на уроке мы отработали применение алгоритма решения линейного уравнения с одной неизвестной. Повторили правила, используемые при решении уравнений.
1. Линейные уравнения.
Эпизод из жизни М.Ю.Лермонтова:
– Задумайте какое угодно число, и я с помощью простых арифметических действий определю его, – предложил М.Ю.Лермонтов.
– Хорошо, я задумал, – сказал один из стоявших вокруг него офицеров…
– Благоволите прибавить к нему еще 25. Теперь не угодно ли прибавить еще 125? Засим вычтите 38. Еще вычтите число, которое вы задумали сначала. Теперь остаток умножьте на 5. Засим полученное число разделите на 2. Теперь посмотрим, что у вас должно получиться. Если не ошибаюсь, число 280?.
Офицер даже привскочил, так поразила его точность вычисления:
– Да, совершенно верно.
На чем основан фокус?
(x + 25 + 125 – 38 – x) * 5 / 2 = 280
Предлагаю задачу : На зимних каникулах из 36 учащихся класса только двое просидели дома, а 25 ребят ходили в кино, 15 – в театр, 17 – в цирк. Кино и театр посетили 11 человек, кино и цирк – 10, театр и цирк – 4. сколько ребят побывало и в кино, и в театре, и цирке?
Решается линейное уравнение: 25 + (3 + Х) + (4 – Х) + Х = 34
Это занимательный элемент напрямую связан с темой урока.
Хозяин нанял работника с таким условием: за каждый рабочий день будет платить ему 20 копеек, а за каждый нерабочий день – вычитать 30 копеек. По прошествии 60 дней работник ничего не заработал. Сколько было рабочих дней?
В решении таких задач используется уравнение.
1) Искусство решать уравнения зародилось у вавилонян, у которых для него было специальное название, перешедшее в арабский язык. Вавилонские математики решали уже уравнения 1-ой и 2-ой степени, а при помощи таблиц – и некоторые виды уравнений 3-ей степени. Узбекский математик аль-Хорезми свою книгу начала IX века, которая, переведенная в XVII веке на латинский язык, стала родоначальником европейских учебников алгебры, называет “Китаб-ал-джабр вал-мукабала”, что в переводе означает “Книга о восстановлении и противосставлении”. “Восстановление” означает превращение вычитаемого ( т.е. “отрицательного”) числа в положительное при перенесении из одной половины уравнения в другую. Так как в те времена отрицательные числа не считались настоящими числами, то операция “ал – джабр” (алгебра), как бы возвращающая число из небытия в бытие, казалась чудом этой науки, которую в Европе после этого называли “великим искусством” рядом с “малым искусством” — арифметикой.
2)Значительный вклад в развитие языка алгебры – символики внес француз Франсуа Виет. В своей работе “Введение в аналитическое искусство” изложил усовершенствованную им теорию уравнений с применением изобретенных символов. Числовые коэффициенты он стал обозначать согласными буквами и придумал новый термин – “коэффициент”, позаимствовав из латинского языка слово “содержащий” . Знаки “+” и “- “ он употреблял в современном значении, неизвестные обозначал гласными буквами латинского алфавита. Дальнейшее усовершенствование алгебраической символики принадлежит Рене Декарту. Именно он ввел для обозначения коэффициентов строчные буквы латинского алфавита: а; в; с;…, а для обозначения неизвестного – последние буквы этого же алфавита – х; у; z. Однако долго еще неизвестные в уравнении писали R (от латинского — корень), а квадрат его буквы буквой q. Слово “равно” Декарт заменил символом.
а) 3х – 12 + 8х – 5; б) 5а – (4 – 3а) + (2а + 1); в) 3(b – 2) + 2(3b + 5).
- Составьте какое-нибудь уравнение вида ax = b, корнем которого является число 3.
- Найдите корень уравнения:
а) 7х = – 1 4; б) – х = 4; в) 0,3 = 9; г) 3х = 0; д) 0х = 0; е) 0х = – 21;
Видео:Линейное уравнение с одной переменнойСкачать

«Линейное уравнение с одной переменной». 7-й класс
Разделы: Математика
Класс: 7
Цели:
Образовательные: cформировать понятие линейного уравнения с одной переменной, закрепить знания обучающихся по данной теме с использованием алгоритма решения линейного уравнения.
Развивающие: развивать умения пользоваться опорным конспектом и вспомогательной литературой для постановки задачи и ее выполнения в ходе решения уравнений; развивать внимательность, собранность и аккуратность; развивать умения работать самостоятельно и в микро группах, ставить перед собой цель и делать выводы, выполнять безошибочно необходимые арифметические вычисления.
Воспитательные: воспитывать внимательность учащихся, создание позитивного отношения учащихся к изученному разделу, умения ясно и четко излагать свои мысли, способствовать математической и общей грамотности.
Видео:7 класс, 4 урок, Линейное уравнение с одной переменнойСкачать

Ход урока
«Уравнение представляет собой наиболее серьёзную и важную вещь в математике».
Лодж О.
I. Организационный момент.
– Сегодня на уроке мы познакомимся с понятием линейного уравнения с одной переменной; рассмотрим алгоритм решения уравнения. Девизом нашего урока будут слова английского физика и изобретателя Сэра Оливера Джозефа Лоджа.
II. Актуализация знаний.
Учитель проводит устное тестирование.
Выберите строку, в которой записано уравнение:
- 48 – 4(5 – 2) = 36
- 48 – 4(5 – х)
- 48 – 4(х – 2) = 36
- 48 – 4(5 – 2)
Какое из чисел является корнем уравнения –2х = 24?
Для какого из уравнений число –2 является корнем?
Приведите подобные слагаемые: 3а + 2а + 4а – 7а
Равносильны ли уравнения:
–2(х — 4) = 4 и 2(х — 4) = –4
- нет
- не знаю
- да
- другой ответ
В ходе тестирования обучающимся предлагает ответить на вопросы:
– Что называется уравнением?
– Что называется корнем уравнения?
– Что значит решить уравнение?
– Какие уравнения называются равносильными?
III. Изучение нового материала.
Учитель предлагает обучающимся из списка выбрать уравнения вида ах =b
- -0,8x 2 =48;
- -1,2х=-3,6;
- 5x 2 -3х=0;
- 6у=2,4;
- 3z=-9
| 2(8 – х) = 10 | Раскрыть скобки в обеих частях уравнения |
| 16 – 2х =10 | Перенести слагаемые, содержащие переменнуюв одну часть, а не содержащие – в другую |
| –2х = 10 – 16 | Привести подобные слагаемые в каждой части |
| –2х = –6 | Разделить обе части уравнения на коэффициент переменной |
| х = 3 |
Затем дает определение линейного уравнения с одной переменной и рассматривает алгоритм решения уравнения.
Учитель предлагает обучающимся выяснить, сколько корней может иметь данное уравнение. Для этого составляют опорный конспект.
Затем учитель разбирает решение линейных уравнений, используя опорный конспект:
Проводит физкультминутку:
Рисуй глазами треугольник
Рисуй глазами треугольник.
Теперь его переверни
Вершиной вниз.
И вновь глазами
ты по периметру веди.
Рисуй восьмерку вертикально.
Ты головою не крути,
А лишь глазами осторожно
Ты вдоль по линиям води.
И на бочок ее клади.
Теперь следи горизонтально,
И в центре ты остановись.
Зажмурься крепко, не ленись.
Глаза открываем мы, наконец.
Зарядка окончилась.
Ты – молодец!
IV. Первичное закрепление изученного материала.
Учитель предлагает обучающимся выполнить задание на доске и в тетрадях.
Задание. Используя опорный конспект, решите уравнения:
- 4(х + 5) = 5(х + 4) – х
- 6х + 3 = 6(х + 5)
- 8х + 4 = 2х + 22
- –12n – 3 = 11n – 3
Обучающиеся на уроке продолжают работу в группах:
1 группа работает самостоятельно, выполняя № 130(в), 132(б, г), один ученик – за доской.
2 и 3 группы – совместно выполняют задание на доске и в тетради №128(а, б, в), 130 (а, е).
Затем 2 и 3 группе учитель предлагает выполнить обучающийся тест, а с 1 группой осуществляет проверку № 130(в), 132 (б, г).
Тест 2 и 3 группе:
| Задание 2 группе | Задание 3 группе |
| 1. Укажите уравнение, которое не является линейным уравнением с одной переменной | |
|
|
| 2. Решите равнение | |
0, 8х – (0, 2х + 4) = 2
| 0,3х – 0,45 =0
|
| 3. Сколько корней имеет уравнение? | |
4х + 3 = 5 + 4( х – 2)
| 2х + 3 = — 6
|
| 4. Найдите корни уравнения | |

| 
|
| 5. Найдите значение а, при котором равны значения выражений | |
–15а + 8 и –17а – 12
| 4а – 2 и а + 4
|
Затем учитель разбирает с 1 группой решение линейных уравнений с параметром.
Задание 1. При каком а уравнение 2ах + 5 = 3х имеет корень, равный –1?
Задание 2. При каких а уравнение 6(ах – 1) + а = 3(а – х) +7 имеет бесконечно много корней?
Задание 3. При каких а уравнение 2(3х – 2а) = 2 + ах не имеет о корней?
А группа 2 и 3 проверяет решение теста с помощью готовых ответов.
| 2 группа. Ответы. 13442 | 3 группа. Ответы. 42113 |
V. Домашнее задание
Учитель предлагает каждому обучающемуся:
1. Карточку для работы с текстом параграфа по плану:
|
2. Дифференцированное домашнее задание по группам:
1 группа №132 (б, г), №138
2 группа №129 (в, ж, г), №133 (б, в)
3 группа №126 (а, г, ж), №128 (г, д)
VI. Итог урока.
Итак, что нового сегодня Вы узнали на уроке?
Дайте определение линейного уравнения. Сколько корней может иметь линейное уравнение? Приведите примеры линейных уравнений с одной переменной.
📽️ Видео
Линейные уравнения с одной переменной, содержащие переменную под знаком модуля. 6 класс.Скачать

Линейное уравнение с одной переменной. Практическая часть. 6 класс.Скачать

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Математика. 6 класс. Линейное уравнение, содержащее переменную под знаком модуля /20.01.2021/Скачать

Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Линейные уравнения с одной переменной . Алгебра . 7 класс .Скачать

Линейное уравнение с одной переменнойСкачать

ЛИНЕЙНЫЕ УРАВНЕНИЯ с одной переменной. §2 алгебра 7 классСкачать

6 класс, 18 урок, Линейные уравнения с одной переменнойСкачать

Математика. 6 класс. Равносильные уравнения. Линейное уравнение с одной переменной /13.01.2021/Скачать

Линейные уравнения с одной переменной, содержащие переменную под знаком модуля. Практ. ч. 6 класс.Скачать

Линейное уравнение с одной переменной | Алгебра 7 класс #17 | ИнфоурокСкачать

Контрольная №1 7 класс. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Решение линейных уравнений с одной переменной. Алгебра 7 класс.Скачать
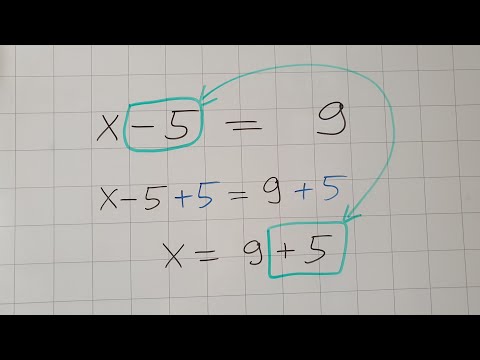
ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ 7 класс МакарычевСкачать








 +
+  = 12
= 12