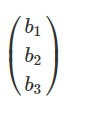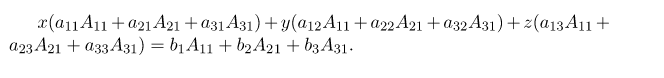В каком году были получены формулы крамера для решения системы линейных уравнений

Видео:Решение системы уравнений методом Крамера.Скачать

Метод Крамера – теорема, примеры решений

Время чтения: 28 минут

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Краткая биография Габриэля Крамера

Габриэль Крамер — (нем. Gabriel Cramer), Швейцария, 31 июля 1704 г. родился в семье врача. Он уже в детстве опередил своих сверстников в развитии интеллектуальной деятельности и проявил завидную способность в математике. В 18 лет успешно защитил дипломную работу. Через два года Крамер выдвинул свою кандидатуру на пост преподавателя в университете в Женеве.

Юноша привлек внимание магистрата, поэтому для него и еще одного кандидата на должность преподавателя был учрежден отдельный факультет математики, где Крамер затем работал в течение последующих нескольких лет.

Учёный очень много путешествовал в Европу, принимая опыт известных математиков того времени, как – Иоганна Бернулли и Эйлера в Базеле, Галлея и де Муавра в Лондоне, Мопертюи и Клеро в Париже и других. Всю жизнь поддерживал с ними тесный контакт.

В 1729 г. Крамер возвращается на должность преподавателя в Женеве. В этот период времени участвует в Парижском конкурсе и занимает заслуженное второе место. Используя свой исключительный талант пишет много статей по самым разным дисциплинам: геометрии, истории, математике, философии.

В 1730 г. он выпускает труд по астрономии.

В 1740 году Иоганн Бёрнулли поручил Крамеру опубликовать сборник его произведений. В 1742 г. Крамер подготовил и опубликовал сборник в 4 -х томах.

В 1744 г. выходит посмертная книга Якоба Бернули брата Иоанна Бернули и двухтомная переписка Лейбницы с Иоанном Бернули. Эти работы вызывали большой интерес ученых по всему миру.

Крамер — один из тех, кто изобрел линейную алгебру. Одна из его наиболее известных работ «Введение в анализ алгебраических кривых», опубликованная в 1750 г. на французском.

В ней Крамер создает систему уравнений по линейным уравнениям и алгоритм, который позже будет носить его имя, — метод Крамера. Габриэль умер во Франции 4 Января 1752 года.

Видео:Решение системы трех уравнений по формулам КрамераСкачать

Метод Крамера – теоремы замещения и аннулирования

Перед решением систем линейных уравнений методом Крамера необходимо изучить две важные закономерности. К ним относятся: теорема аннулирования; теорема замещения.

Теорема замещения. Складывая произведения алгебраического дополнения какого-то столбца, а также произвольные чисел b1, b2, b3, получается новый определитель, в котором значения заменяют соответствующие элементы первоначального определения, соответствующие данному алгебраическому дополнению.

Теорема аннулирования. В сумме произведения компонентов одного столбца или таблицы и алгоритмических дополнений соответствующих элементов другого столбца – будут равняться нулю.

Видео:Решение системы уравнений методом Крамера 2x2Скачать

Применение метода Крамера для решения систем линейных уравнений (СЛАУ)

Для поиска ответов по задачам для решения систем линейных уравнений актуальна эта методика. Метод Крамера позволяет находить решение системы с количеством строк равным количеству неизвестного. Так решаются квадратные уравнения. В процессе нужно вычислить матричные определители, в том числе основные, и дополнительные, полученные с помощью замены одного столбца основного определителя на столбец со свободными членами системы алгоритмов. На рисунке можно найти наглядное представление алгоритма.

Для этого необходимо применить метод Крамера СЛАУ:

Рассмотрим решение системы уравнений методом Крамера:

Первое: вычислим определитель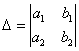, а именно – определитель системы.

Если [Delta=0] система имеет только 1 решение, чтобы найти корни, следует сделать вычислить еще два определителя:

На практике данные определители обычно могут быть обозначены обычной латинской буквой D. Чтобы найти корни уравнения используем следующую формулу:

Пример: Решите систему уравнений линейным методом Крамера

Решение: Из уравнения следует, что коэффициенты уравнения велики, в правой части уравнения видим десятичные дроби с запятой. Запятая – крайне редко можно увидеть в практике по математике, эта система взята из эконометрической задачи.

1. Есть вариант выразить одну переменную через другую, это не самый удобный способ, так как мы получим дроби, с которыми невозможно будет работать, и будет хромать оформление самого решения.
2. В таких случаях применимо правило Крамера.

Оба корня имеют бесконечные хвосты, решение дает лишь приближенное значение, что допустимо, если это задачи по эконометрике. Данное условие решается по готовым формулам, однако, есть одна деталь. Если используется данный метод, то обязательным условием, является использование вот этого фрагмента: 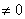это значит, что уравнение имеет одно решение». Если этого не сделать, то при проверке вас могут наказать за пренебрежением теоремой Крамера.

Оба корня имеют бесконечные хвосты, решение дает лишь приближенное значение, что допустимо, если это задачи по эконометрике. Данное условие решается по готовым формулам, однако, есть одна деталь. Если используется данный метод, то обязательным условием, является использование вот этого фрагмента: [neq 0] это значит, что уравнение имеет одно решение». Если этого не сделать, то при проверке вас могут наказать за пренебрежением теоремой Крамера.

Важно сделать проверку, ее удобно провести на калькуляторе: подставляем приближенные значения [a approx-0,35 quad b approx 37,77] в левую часть каждого уравнения системы. По итогу с небольшой погрешностью получаться числа, которые находятся в правых частях.

Метод Крамера — это простой метод решения линейных алгебраических уравнений. Этот вариант применим только к СЛАУ, в которых количество уравнений согласуется с неизвестным числом, а определитель не равен нулю.

Поэтому, когда вы изучили все шаги, вы можете продолжать использовать метод Крамера для решения алгоритма уравнения. Записываем их по порядку:

• Найти главный определитель матрицы:

Важно, чтобы определитель не имел значения – 0.

• Ищем определители:

В итоге получаем, определители матриц, которые мы вывели из матрицы A заменяя столбцы на свободные члены.

• Найдем неизвестные переменные значения:

Тут важно помнить тождества Крамера, при помощи которых, можно найти корни или по-другому неизвестные переменные.

• Выполняем проверку:

Мы проверяем решение, подставляя x, y и z в исходную СЛАУ. Все уравнения в абсолютной системе необходимо преобразовать в тождества. Вы также можете вычислить произведение матрицы A * X. Если результатом является матрица, равная B, система решена правильно. Если он не равен B, то одно из уравнений, вероятно, содержит ошибку.

Давайте сначала рассмотрим систему, состоящую из двух линейных уравнений, потому что она проще и поможет вам понять, как правильно использовать правило Крамера. Если вы разбираетесь в простых и коротких уравнениях, вы можете решать более сложные системы из трех уравнений с тремя неизвестными.

Среди прочего, существуют уравнения с двумя переменными, и решение этих уравнений целиком связано с правилом Крамера.

Пример. Таким образом, дана система, состоящая из двух линейных уравнений:

• Ищем главный определитель системы:

• Это означает, что если [Delta=0], то либо у системы много решений, либо у системы нет решений. В этом случае нет смысла использовать правило Крамера, потому что решение не будет работать, и вам нужно запомнить метод Гаусса, который можно использовать для быстрого и простого решения этого примера.

Если [Delta neq 0], система имеет только одно решение, но для этого необходимо вычислить два других определителя и найти корень системы.

На практике определитель обычно может быть представлен не только [Delta], но и латинской буквой D, что тоже правильно.

• Найти корни уравнения несложно, ведь главное знать формулу:

Теперь, когда мы можем решить двух линейные уравнения, мы можем решить трех линейные уравнения без каких-либо проблем. Для этого мы рассмотрим систему:

Здесь алгебраическим дополнением элементов является первый столбец [A_, A_, A_]. При решении не забывайте и о других элементах. Следовательно, в системе линейных уравнений вам нужно найти три неизвестных — x, y, z и другие известные элементы.

Составим определитель системы из коэффициентов неизвестных: мы умножаем каждый член уравнения на [A_, A_, A_] — алгебраическое дополнение элементов в первом столбце (коэффициент при x), а затем складываем все три уравнения вместе. У нас есть:

Согласно теореме о разложении коэффициент при x равен [Delta].Коэффициенты при y и z будут равняться нулю по теореме аннулирования. Правая часть равенства по теореме замещения даёт новый определитель, который называется вспомогательным и обозначается:

Далее, можно записать равенство:

Для нахождения y и z перемножим каждое из уравнений изначальной системы в первом случае соответственно [A_, A_, A_] во втором [A_, A_, A_] и прибавим значение.

Видео:Метод Крамера для решения систем линейных алгебраических уравнений (СЛАУ) в ExcelСкачать

Метод Гаусса и Крамера

В данной работе представлены: определение метода Гаусса и Крамера; мини биография (годы жизни) Иоганн Карл Фридрих Гаусс, Габриэль Крамер; примеры и их решения.

Просмотр содержимого документа
«Метод Гаусса и Крамера»

Прямоугольная таблица из m , n чисел, содержащая m – строк и n – столбцов, вида:

называется матрицей размера m  n

Числа, из которых составлена матрица, называются элементами матрицы.

Положение элемента а i j в матрице характеризуются двойным индексом:

первый i – номер строки;

второй j – номер столбца, на пересечении которых стоит элемент.

Сокращенно матрицы обозначают заглавными буквами: А, В, С…

Коротко можно записывать так:

Иоганн Карл Фридрих Гаусс (30 апреля 1777, Брауншвейг — 23 февраля 1855, Гёттинген)

Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Система т линейных уравнений с п неизвестными имеет вид:

a i j — коэффициенты при неизвестных.

b i — свободные члены (или правые части)

Система линейных уравнений называется совместной , если она имеет решение, и несовместной , если она не имеет решения.

Совместная система называется определенной , если она имеет единственное решение и неопределенной , если она имеет бесчисленное множество решений.

Две совместные системы называются равносильными , если они имеют одно и то же множество решений.

К элементарным преобразованиям системы отнесем следующее:

• перемена местами двух любых уравнений;
• умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;
• прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.

Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с тремя неизвестными в случае, когда существует единственное решение:

1-ый шаг метода Гаусса

На первом шаге исключим неизвестное х 1 из всех уравнений системы (1), кроме первого. Пусть коэффициент . Назовем его ведущим элементом. Разделим первое уравнение системы (1) на а 11 . Получим уравнение:

Исключим х 1 из второго и третьего уравнений системы (1). Для этого вычтем из них уравнение (2), умноженное на коэффициент при х 1 (соответственно а 21 и а 31 ).

Система примет вид:

Верхний индекс (1) указывает, что речь идет о коэффициентах первой преобразованной системы.

2-ой шаг метода Гаусса

На втором шаге исключим неизвестное х 2 из третьего уравнения системы (3) . Пусть коэффициент . Выберем его за ведущий элемент и разделим на него второе уравнение системы (3) , получим уравнение:

Из третьего уравнения системы (3) вычтем уравнение (4), умноженное на Получим уравнение:

Предполагая, что находим

В результате преобразований система приняла вид:

Система вида (5) называется треугольной .

Процесс приведения системы (1) к треугольному виду (5) (шаги 1 и 2 ) называют прямым ходом метода Гаусса .

Нахождение неизвестных из треугольной системы называют обратным ходом метода Гаусса.

Для этого найденное значение х 3 подставляют во второе уравнение системы (5) и находят х 2 . Затем х 2 и х 3 подставляют в первое уравнение и находят х 1 .

Если в ходе преобразований системы получается противоречивое уравнение вида 0 = b , где b  0, то это означает, что система несовместна и решений не имеет.

В случае совместной системы после преобразований по методу Гаусса, составляющих прямой ход метода, система т линейных уравнений с п неизвестными будет приведена или к треугольному или к ступенчатому виду.

Треугольная система имеет вид:

Такая система имеет единственное

решение, которое находится в

результате проведения обратного хода метода Гаусса.

Ступенчатая система имеет вид:

Такая система имеет бесчисленное

Рассмотрим на примере

• Покажем последовательность решения системы из трех уравнений методом Гаусса

• Поделим первое уравнение на 2, затем вычтем его из второго (a 21 =1, поэтому домножение не требуется) и из третьего, умножив предварительно на a 31 =3

• Поделим второе уравнение полученной системы на 2, а затем вычтем его из третьего, умножив предварительно на 4,5 (коэффициент при x 2 )

Метод Крамера—способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы. Создан Габриэлем Крамером в 1751 году.

Габриэль Крамер (31 июля 1704, Женева, Швейцария—4 января 1752, Баньоль-сюр-Сез, Франция)

Рассмотрим систему линейных уравнений с квадратной матрицей A , т.е. такую, у которой число уравнений совпадает с числом неизвестных:

a 11 x 1 +a 12 x 2 +…+a 1n x n =b 1

a 21 x 1 +a 22 x 2 +…+a 2n x n =b 2

a n1 x 1 +a n2 x 2 +…+a nn x n =b n

• a 11 x 1 +a 12 x 2 +…+a 1n x n =b 1 a 21 x 1 +a 22 x 2 +…+a 2n x n =b 2 … … a n1 x 1 +a n2 x 2 +…+a nn x n =b n
• a 11 x 1 +a 12 x 2 +…+a 1n x n =b 1 a 21 x 1 +a 22 x 2 +…+a 2n x n =b 2 … … a n1 x 1 +a n2 x 2 +…+a nn x n =b n
• a 11 x 1 +a 12 x 2 +…+a 1n x n =b 1 a 21 x 1 +a 22 x 2 +…+a 2n x n =b 2 … … a n1 x 1 +a n2 x 2 +…+a nn x n =b n

Имеет единственное решение тогда и только тогда, когда определитель матрицы этой системы отличен от нуля:

a 11 a 12 … a 1n

a 21 a 22 … a 2n

a n1 a n2 … a nn

• a 11 a 12 … a 1n a 21 a 22 … a 2n … … a n1 a n2 … a nn

В этом случае решение можно вычислить по формуле Крамера

Для получения значения x k в числитель ставится определитель, получающийся из det(A) заменой его k- го столбца на столбец правых частей

• Пример. Решить систему уравнений :

Найдите оставшиеся компоненты решения.

• Формулы Крамера не представляют практического значения в случае систем с числовыми коэффициентами: вычислять по ним решения конкретных систем линейных уравнений неэффективно, поскольку они требуют вычисления (n+1)-го определителя порядка n , в то время как метод Гаусса фактически эквивалентен вычислению одного определителя порядка n . Тем не менее, теоретическое значение формул Крамера заключается в том, что они дают явное представление решения системы через ее коэффициенты. Например, с их помощью легко может быть доказан результат
• Решение системы линейных уравнений с квадратной матрицей A является непрерывной функцией коэффициентов этой системы при условии, что det A не равно 0 .

Найдите оставшиеся компоненты решения.

• Кроме того, формулы Крамера начинают конкурировать по вычислительной эффективности с методом Гаусса в случае систем, зависящих от параметра.
• зависящей от параметра , определить предел отношения компонент решения:

• В этом примере определитель матрицы системы равен . По теореме Крамера система совместна при . Для случая применением метода Гаусса убеждаемся, что система несовместна. Тем не менее, указанный предел существует. Формулы Крамера дают значения компонент решения в виде

и, хотя при каждая из них имеет бесконечный предел, их отношение стремится к пределу конечному.

Приведенный пример поясняет также каким образом система линейных уравнений, непрерывно зависящая от параметра, становится несовместной: при стремлении параметра к какому-то критическому значению (обращающему в нуль определитель матрицы системы) хотя бы одна из компонент решения «уходит на бесконечность».

• В.С. Щипачев, Высшая математика
• Ильин В. А., Позняк Э. Г. Линейная алгебра: Учебник для вузов.
• Волков Е.А. Численные методы.
• В.Е. Шнейдер и др., Краткий курс высшей математики,том I.

Видео:10. Метод Крамера решения систем линейных уравнений.Скачать

Метод Крамера

Видео:Решение систем линейных алгебраических уравнений методом Крамера.Скачать

Общие понятия

Методом Крамера, или как его еще называют, правилом Крамера, является такой способ нахождения неизвестных для заданной системы уравнений. Такой метод используется лишь тогда, когда количество неизвестных равняется числу уравнений системы, иными словами, матрица, образованная из заданной системы уравнений, должна быть квадратной без нулевых строк и ее главный определитель не должен равняться нулю. Рассмотрим теорему Крамера:

При условии, что главный детерминант матрицы (D) , состоящей их коэффициентов системы уравнений, не равняется нулю, эта система уравнений считается совместной, с существующим для нее единственным решением. Неизвестные этих систем линейных уравнений рассчитывают по формуле Крамера: (x_i=) .

Порядок определения неизвестных по методу Крамера включает такие действия:

1. Сперва рассчитывают главный детерминант матрицы (D) . Если найденный детерминант равняется нулю, то для данной системы уравнений не существует решений или их существует бесконечное множество. В таком варианте рекомендуют воспользоваться методом Гаусса для определения базисного решения.
2. Если же главный детерминант не равняется нулю, то эту систему уравнений рассчитывают методом Крамера. Левый столбик главной матрицы заменяют на столбик свободных членов и рассчитывают детерминант (D_1) .
3. Проделывают те же действия для всех следующих столбиков по порядку и определяют детерминанты (D_1, D_2, …, D_n) , где (n) – число столбиков.
4. Теперь, имея все детерминанты, рассчитывают все переменные от (x_1) до (x_n) .

Не нашли что искали?

Просто напиши и мы поможем

Видео:2 минуты на формулы Крамера ➜ Решение систем уравнений методом КрамераСкачать

Способы расчета определителей матриц

Для расчета определителей матриц, размером более 2х2, применяют различные способы, рассмотрим их подробнее:

1. Метод Гаусса, второе его название – метод понижения порядка определителя. При данном методе матрицу преобразуют к форме треугольника, после этого перемножают составляющие главной диагонали. Стоит отметить, что при применении этого метода запрещено множить или делить строки, или столбцы на числа, не вынося их как множители или делители.

При данном методе можно лишь плюсовать или минусовать строки, или столбцы друг с другом, перед этим перемножив минусуемую строку на нуль. Необходимо также помнить, что во время перестановки столбиков или строк местами, нужно изменять знак матрицы.

2. Правило треугольников или правило Саррюса, которые очень похожи между собой. Для применения правила Саррюса, вначале записывают матрицу, а потом справа от нее снова записывают ее первый и второй столбики.

Числа матрицы и этих столбиков соединяют диагоналями, числа, что лежат на главной и параллельных диагоналях, записывают с плюсом, а числа, что лежат на побочной и параллельных ей диагоналях – с минусом.

Правило треугольников заключается в том, что для расчета детерминанта произведения всех чисел, что соединены на рисунке красной линией слева, записывают с плюсом, а те, что соединены так же справа – с минусом.

Оба способа применимы для матриц величиной 3х3.

3. Для расчета систем линейных арифметических уравнений с четырьмя неизвестными, стоит отметить, что более применимым для расчета определителей является метод Гаусса, либо также применяют метод миноров.

Видео:Формулы КРАМЕРАСкачать

Использование метода Крамера

Метод Крамера применяют для определения неизвестных в системах линейных арифметических уравнений.

Разберем применение метода Крамера для расчета системы уравнений с двумя неизвестными:

( begin a_1 x_1+a_2 x_2=b_1 \ a_3 x_1+a_4 x_2=b_2 end)

Преобразуем ее в такую форму:

Рассчитаем главный определитель системы, его так же именуют детерминантом основной матрицы:

Далее, если главный детерминант не равняется нулю, рассчитываем систему линейных уравнений методом Крамера. Для этого рассчитываем все детерминанты, заменяя поочередно столбики основной матрицы столбиками свободных членов:

Затем по формуле Крамера рассчитаем все переменные:

Рассмотрим задачу с конкретными уравнениями. Рассчитаем данную систему уравнений методом Крамера:

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

1. Определим главный детерминант по вышеизложенному принципу:

2. Далее рассчитаем остальные детерминанты:
(D_1=begin21& -2&4\9&4&-2\10& -1&1end=) (21∙4∙(-1)+2∙(-2)∙10+4∙9∙(-1)-4∙4∙10-9∙(-2)∙(-1)-(-1)∙2∙21=)
(=-84-40-36-160-18+42=-296.)

3. Затем рассчитаем наши неизвестные, применяя формулы Крамера:

📺 Видео

Формулы Крамера для системы двух линейных уравненийСкачать

Решение СЛАУ методом Крамера. Линейная алгебраСкачать

Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

Формулы Крамера для решения систем уравненийСкачать

Линейная алгебра, 8 урок, Метод КрамераСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

Решение системы уравнений с тремя неизвестными с помощью формул Крамера | Высшая математикаСкачать

Доказательство формул Крамера для системы двух уравненийСкачать

Решение системы уравнений методом Крамера 4x4Скачать

Матричный метод решения систем уравненийСкачать

Лекция 10. Решение систем линейных уравнений по формулам КрамераСкачать