Видео:ЕГЭ. Физика. Уравнение состояния идеального газа. ПрактикаСкачать

Ваш ответ
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

решение вопроса
Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Похожие вопросы
- Все категории
- экономические 43,414
- гуманитарные 33,633
- юридические 17,906
- школьный раздел 608,054
- разное 16,856
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Уравнения состояния реальных газов
Вопрос №1
Идеальный газ. Законы идеальных газов
Идеальным называется газ, у которого объемы молекул бесконечно малы и отсутствуют силы межмолекулярного взаимодействия. Молекулы идеального газа представляют собой материальные точки, взаимодействие между которыми ограничено молекулярными соударениями.
Любой реальный газ тем ближе к идеальному, чем ниже его давление и выше температура. Например, окружающий нас воздух можно считать идеальным газом. Понятие идеального газа и законы идеальных газов полезны в качестве предела законов реального газа.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
На практике часто приходится иметь дело с газами при невысоких давлениях, поэтому расчеты различных термодинамических процессов с достаточной степенью точности можно проводить по уравнениям идеального газа.
Закон Авогадро
Согласно этому закону, все газы при одинаковых температурах и одинаковом давлении содержат в одном и том же объеме одинаковое число молекул. Большую техническую значимость имеет следствие из закона Авогадро: объемы киломолей различных газов равны, если они находятся при одинаковых температурах и давлениях. При нормальных физических условиях (Т= 273,15 К, р = 760 мм рт. ст.) объем киломоля любого вещества равен Vµ=µν=22,4 м 3 /кмоль.Напомним, что киломолем называется количество вещества в килограммах, численно равное его молекулярной массе.
Этот закон был открыт независимо друг от друга английским физиком Р. Бойлем и французским ученым Э. Мариоттом. Ими было доказано, что при постоянной температуре газа произведение давления газа на его объем есть величина постоянная, т.е. при
рV= const и рv = const.
Закон Гей-Люссака
Этот закон устанавливает, что если в процессе нагрева или охлаждения газа давление подцерживается постоянным, то объем изменяется пропорционально абсолютной температуре, т.е. если
Р = const, то и v/ Т = const.
Если же мы рассмотрим процесс нагрева или охлаждения газа в сосуде постоянного объема (v= const), то р/Т = const.
Уравнение состояния идеального газа
Для 1 кг газа Клапейроном установлено уравнение состояния рv = RT, в котором газовая постоянная Rимеет для каждого газа свое постоянное значение. Измеряется Rв Дж/кг-К и имеет вполне определенный физический смысл — это работа, совершаемая 1 кг газа при его нагреве на один кельвин при постоянном давлении. Для газа с произвольной массой M/(кг) уравнение состояния имеет вид
Для одного киломоля вещества уравнение состояния (получено Д.И. Менделеевым) имеет вид рVµ =µRT, где µR— универсальная газовая постоянная, которая одинакова для всех газов и равна 8314 Дж/кмольК.
Во всех этих уравнениях давление подставляется в Па, температура — в К, объем — в м 3 и удельный объем — в м 3 /кг.
В резервуаре объемом 10 м 3 находится азот при избыточном давлении 100 кПа и при температуре 27 °С. Атмосферное давление равно 750 мм рт. ст. Требуется найти массу и плотность азота.
Выразим атмосферное давление в паскалях: рб = 10 5 Па.
Абсолютное давление газа равно:p =ри +рб = 100 • 10 3 + 10 5 = = 2 • 10 5 Па.
Газовая постоянная азота равна (µ = 28 кг/кмоль)
R = 8314/28 = 297 Дж/кгЧК. Масса газа равна
М =рV/RT= 2*10 5* 10/297 • (273,15 + 27) = 22,43 кг.
р = M/V= 22,43/10 = 2,243 кг/м 3 .
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
РЕАЛЬНЫЕ ГАЗЫ
Свойства реальных газов
Свойства реальных газов значительно отличаются от свойств идеальных газов, причем отличия тем значительнее, чем выше давление и ниже температура газа. Это объясняется тем, что молекулы реальных газов имеют конечный объем и между ними существуют силы межмолекулярного взаимодействия. Уравнение состояния 1 кг реального газа имеет вид
где z= φ(р, T) — коэффициент сжимаемости, который может быть как больше, так и меньше единицы.
При проведении термодинамических расчетов с реальными газами нужно учитывать зависимость внутренней энергии, энтальпии и теплоемкости не только от температуры, но и от давления газа. При одном и том же давлении какое-либо вещество в зависимости от температуры может находиться в разных состояниях.
Из физики известно, что любое вещество может находиться в твердом, жидком или газообразном состоянии. Эти состояния будем называть фазами, а процесс перехода из одного состояния в другое — фазовым переходом.
При определенных условиях могут существовать одновременно две фазы вещества, например, лед и жидкость, пар и жидкость. Если пар и жидкость находятся в состоянии равновесия, то пар называется насыщенным.
У всех веществ фазовые переходы происходят при определенных физических параметрах, поэтому рассмотрение свойств реальных газов можно начать на примере вещества, которое является основным рабочим телом в циклах тепловых электростанций, в том числе и атомных. Этим рабочим телом является вода, и не только потому, что она относительно дешева и нетоксична, а потому, что она обладает благоприятными для работы термодинамическими свойствами.
Рассмотрим диаграмму «v—p» воды и водяного пара, на которой изобразим границы между фазами (рис. 1.1). В области а находится в равновесии смесь льда и некипящей воды, в области Ь находится некипящая вода, в области с находится смесь кипящей воды и водяного пара, в области d— перегретый водяной пар. Прямой 1-2 показан изобарный процесс подвода теплоты.
Показанные на рис. 1.1 кривые называются пограничными; кривые, ограничивающие с двух сторон область с, называются левой и правой пограничными кривыми. Им соответствуют кипящая вода (левой) и сухой насыщенный пар (правой). Область между этими кривыми называется областью влажного насыщенного пара — в этой области находятся в равновесии сухой насыщенный пар и кипящая вода. Смесь сухого насыщенного пара и кипящей воды называют влажным насыщенным паром. Масса влажного насыщенного пара равна
где М’ — масса кипящей воды и М» — масса сухого насыщенного пара.
В дальнейшем все параметры, относящиеся к кипящей жидкости, будут иметь индекс «штрих» (р’, h’и т.д.), а все параметры, относящиеся к сухому насыщенному пару,— индекс «два штриха» (р’, h» и т.д.).
Температуру и давление насыщенного пара принято обозначать Тн и рн. В то же время в ряде литературных источников их обозначают Тs и рs (буква s является первой буквой английского слова sаturation — насыщение). Отношение массы сухого насыщенного пара к общей массе влажного насыщенного пара называется степенью сухости и обозначается х. Ясно, что на левой пограничной кривой х = 0, а на правой — х = 1. Разность <1-х) называется степенью влажности.
Чем выше давление пара, тем меньше расстояние по горизонтали между левой и правой пограничными кривыми, а при определенном давлении пара эти кривые смыкаются. Точка, в которой исчезают различия в свойствах кипящей жидкости и сухого насыщенного пара, называется критической (точка к на рис. 1.1).
Термические параметры различных веществ в критической точке различны. Эти параметры для ряда химических веществ приведены в табл. 1
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Таблица 1 Критические параметры веществ
| Вещество | Tкр, К | pкр,МПа | ρкр, кг/м 3 |
| Азот N2 | 3,40 | ||
| Водород Н2 | 33,2 | 1,29 | |
| Водяной пар H2O | 647,12 | 22,115 | |
| Кислород О2 | 5,05 | ||
| Ртуть Нg | — | ||
| Диоксид углерода СО2 | 7,38 |
При сверхкритическом давлении не может быть влажного насыщенного пара. Если давление пара больше критического и постоянно по величине (р > ркр), то при подводе (или отводе) теплоты физические параметры (удельный объем, энтальпия и др.) меняются плавно, в то же время наблюдается резкое изменение тепло-емкостей сp исvв тех процессах, где сверхперегретая вода переходит в сверхперегретый водяной пар.
Уравнения состояния реальных газов
Известно значительное число уравнений состояния реальных газов, и одна из самых удачных попыток была сделана Ван-дер-Ваальсом, который получил уравнение в виде
Слагаемое a/v 2 учитывает внутреннее давление, обусловленное силами взаимодействия молекул газа, а величина b— уменьшение объема, в котором движутся молекулы реального газа. Если по этому уравнению находить величины удельных объемов реальных газов, то уравнение (1) имеет три действительных корня при Т Ткр . Точность вычислений по этому уравнению невелика.
В самой общей форме уравнение состояния реальных газов имеет вид
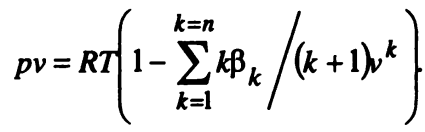
где 𝛽k — вириальные коэффициенты, зависящие от температуры газа.
Число членов ряда в уравнении (2) может быть достаточно велико, поэтому расчеты по этому уравнению вызывают значительные трудности.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
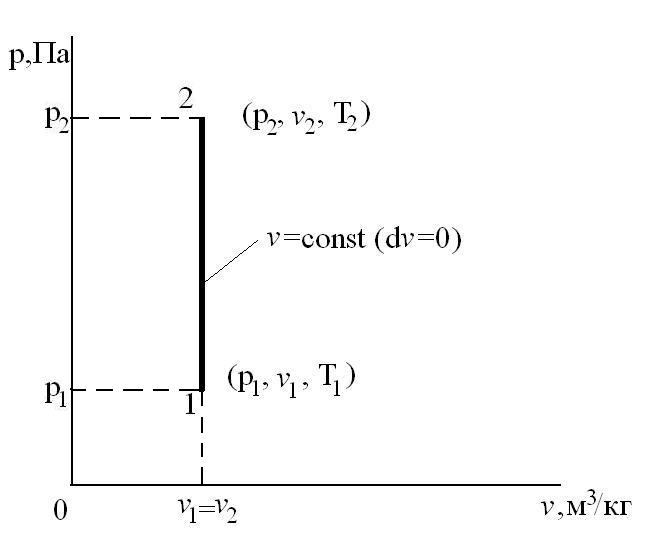
Изохорный процесс – это процесс сообщения или отнятия теплоты от газа при постоянном объеме v=const.
Этот процесс используется как подготовительный процесс в циклах.
Соотношение между параметрами для конечного участка процесса 1-2 определяется законом Шарля: 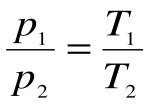
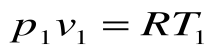
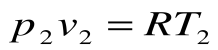
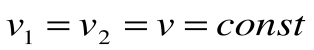
Поскольку работа расширения в этом процессе равна нулю: 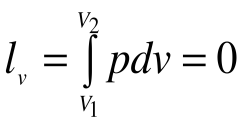
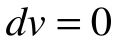
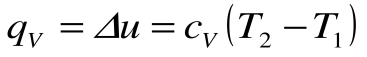
Таким образом, подведенная к газу в изохорном процессе теплота целиком идет на увеличение его внутренней энергии. Для ТП 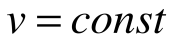
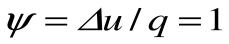


| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
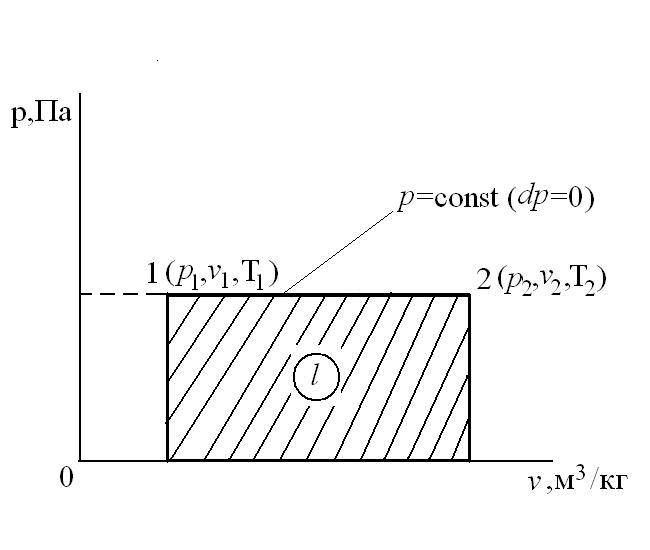
Изобарный процесс – это процесс сообщения или отнятия теплоты от газа при постоянном давлении р=const.
Соотношение между параметрами в процессе р=const: 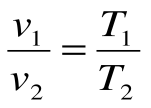


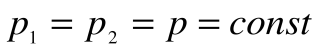
Работа расширения 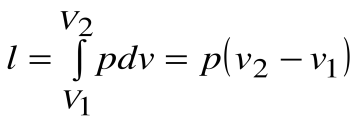
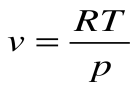
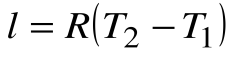
Следовательно, удельная газовая постоянная R— это работа, совершаемая 1кг газа в процессе p=const при его нагревании на один градус. Размерность R: Дж/кгК. Уравнение 1-го закона термодинамики в этом случае имеем вид:
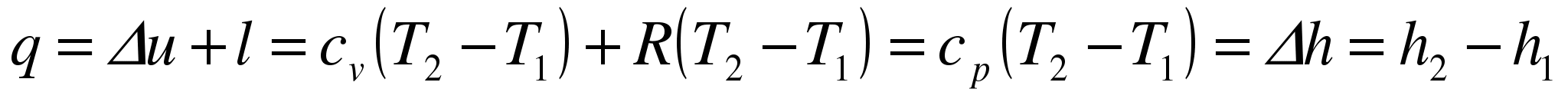
Таким образом, вся теплота, подведенная к газу в изобарном процессе, расходуется на увеличение его энтальпии.
Коэффициент распределения теплоты в процессе р=const равен:
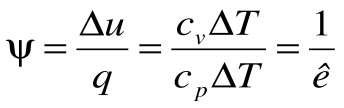
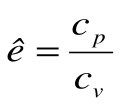
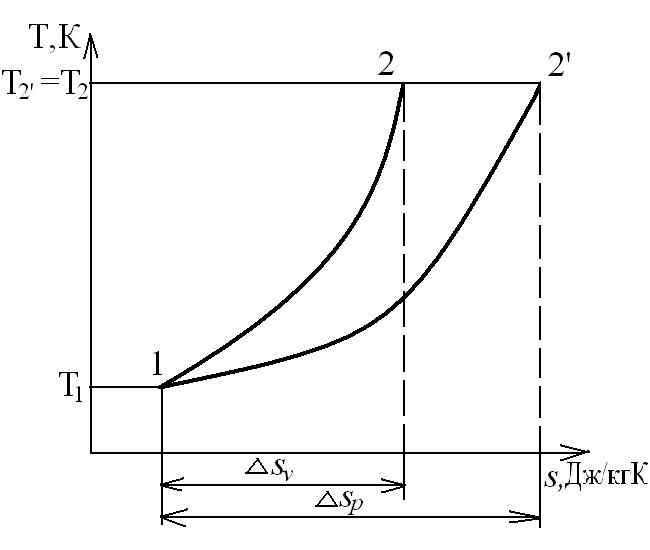
В T-s координатах взаимное положение изобары и изохоры имеет вид:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
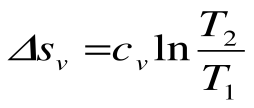
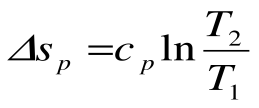
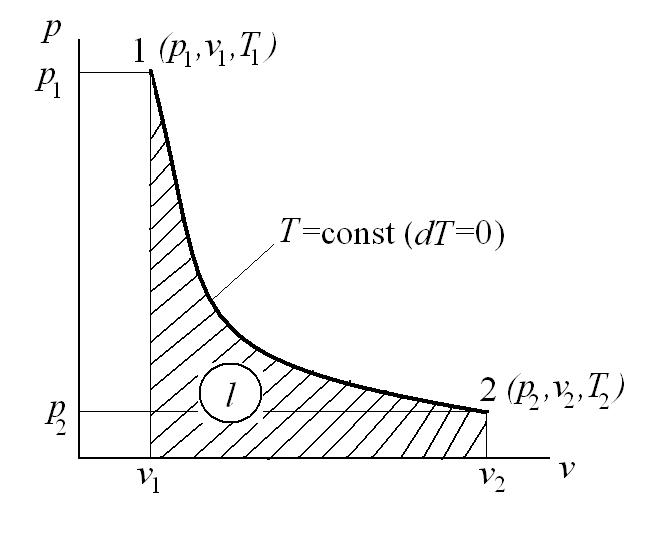
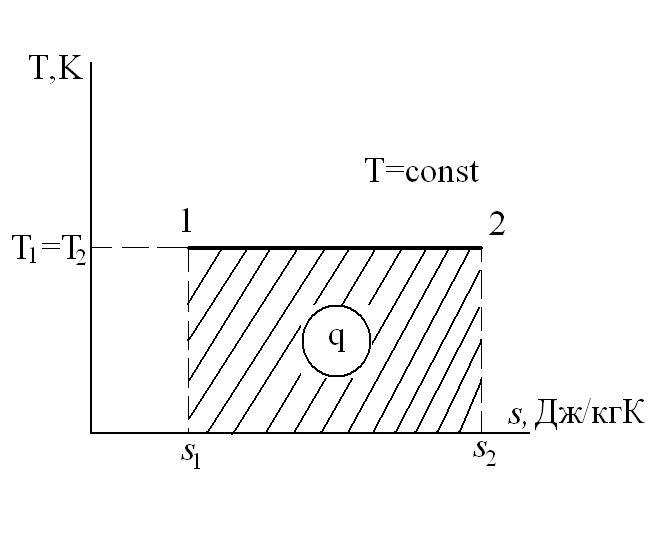
Изотермический процесс – это процесс сообщения или отнятия теплоты от газа при постоянной температуре
При Т=const из уравнения состояния 
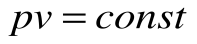
Тогда 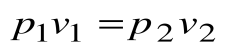
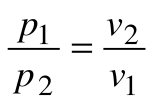
Из уравнения 1-го закона термодинамики 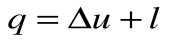
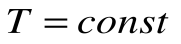
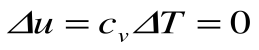
Изменение энтальпии в процессе T=const равно:
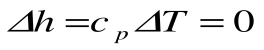
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
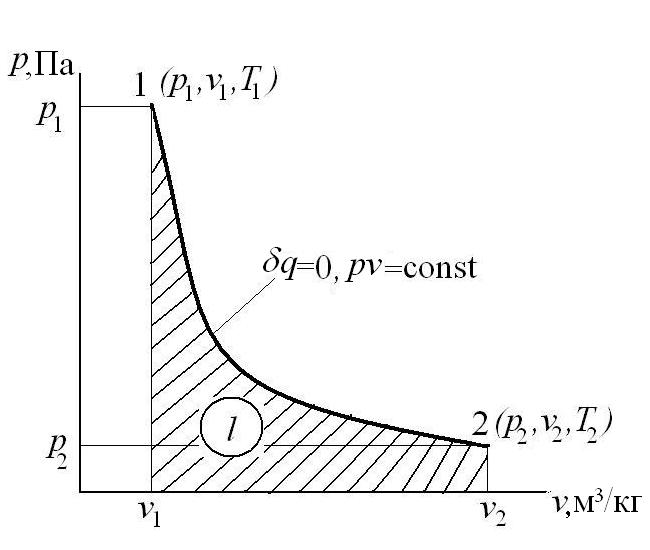
Работа расширения 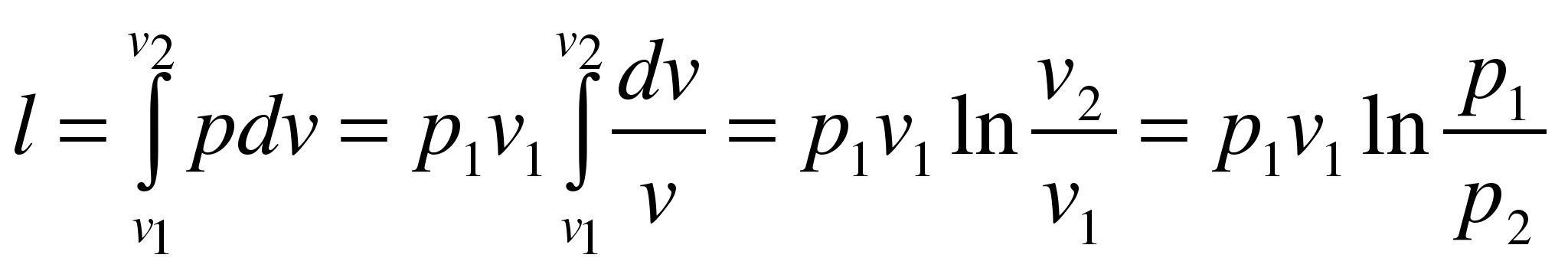
Коэффициент распределения теплоты
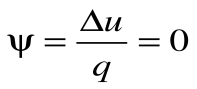
Тогда теплоемкость 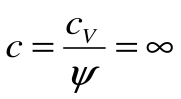
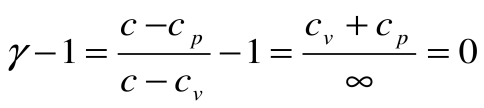
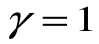
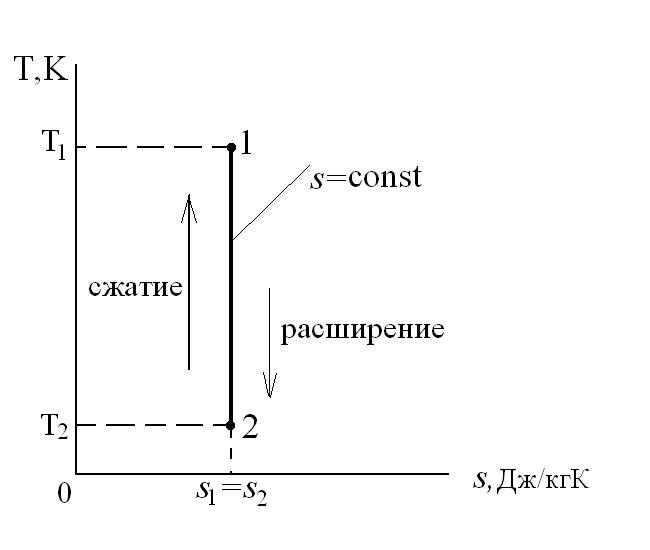
Адиабатный процесс – это процесс, протекающий без внешнего теплообмена, т.е. q=0 и 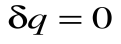
Если записать для этого случая уравнения 1-го закона термодинамики в виде:
1. 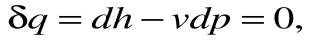
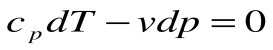
2. 
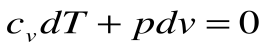

Тогда после интегрирования выражения 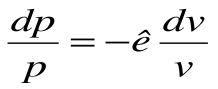

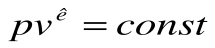
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
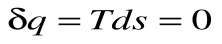
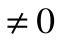
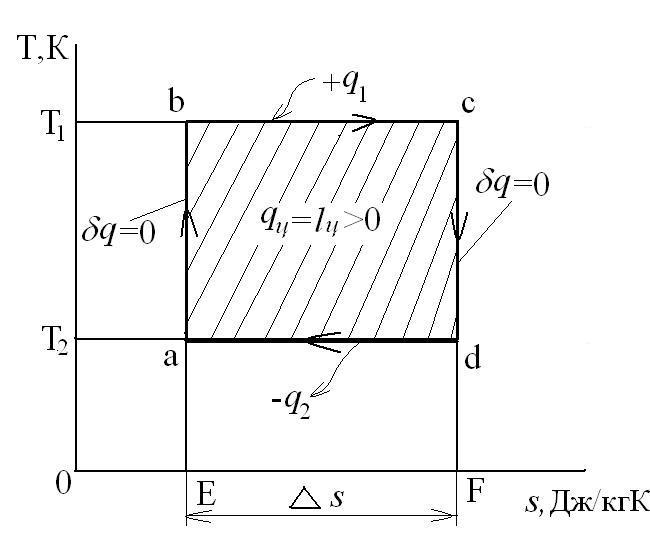
Для теплового двигателя цикл Карно – прямой цикл, состоящий из двух адиабат и двух изотерм, а для тепловых трансформаторов используется обратный цикл Карно. Тепловые машины, работающие по циклу Карно, имеют наибольшие значения термических кпд по сравнению с любым другим циклом при одинаковых предельных температурах цикла Т1 и Т2.
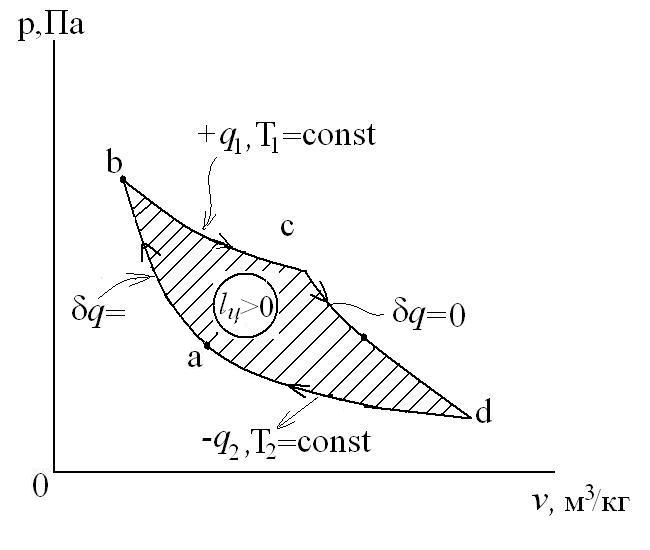
Рассмотрим прямой цикл Карно.
Графически в p-v и T-s координатах этот цикл можно представить в виде:
где ab – адиабатное сжатие ТРТ;
bc – подвод теплоты q1 в изотермическом процессе при Т1=const;
cd – адиабатное расширение ТРТ;
da – отвод теплоты 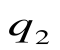
q1 = площадь bсFEb – теплота, затраченная на совершение цикла 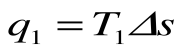
q2 = площадь adFЕa – теплота, отведенная в холодильник 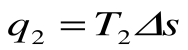
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
Тогда термический кпд прямого цикла Карно будет равен:
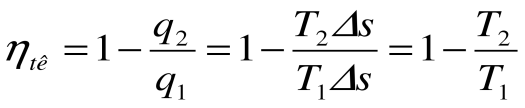
Таким образом, термический кпд цикла Карно зависит только от предельных температур источника и холодильника и не зависит от рода рабочего тела. (Первая теорема Карно). Температура Т1 и Т2 являются основными параметрами цикла Карно, которые полностью определяют этот цикл.
При Т1=Т2 термический кпд цикла Карно 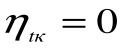
При Т2=0 или Т1= 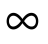
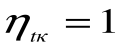
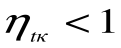
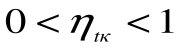
Любое заключение, вытекающее из анализа прямого цикла Карно, можно рассматривать как формулировку второго закона термодинамики.
В двух разобщенных между собой теплоизолированных сосудах А и В содержатся газы, в сосуде А – аргон, в сосуде В– водород, объем сосуда А– 150 л, сосуда В – 250 л. Давление и температура аргона – р1, t1, водорода – р2, t2. Определить давление и температуру, которые установятся после соединения сосудов и смешения газов. Теплообменом с окружающей средой пренебречь
Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

6.2. Уравнения состояния реального газа
Наиболее простым и качественно верно отображающим поведение реального газа, является уравнение Ван-дер-Ваальса:
(P + a/ n 2 )·( n – b) = R·T . (6.3)
а, b – постоянные величины, первая учитывает силы взаимодействия, вторая учитывает размер молекул.
a/ n 2 – характеризует добавочное давление, под которым находится реальный газ вследствие сил сцепления между молекулами и называется внутренним давлением. Для жидких тел это давление имеет большие значения (например, для воды при 20 0 С составляет 1050 Мпа), а для газов из-за малых сил сцепления молекул оно очень мало. Поэтому внешнее давление, под которым находится жидкость, оказывает ничтожное влияние на её объем, и жидкость считают несжимаемой. В газах в виду малости значения a/ n 2 внешнее давление легко изменяет их объем.
Уравнение Ван-дер-Ваальса качественно верно отображает поведение жидких и газообразных веществ, для двухфазных состояний оно неприменимо.
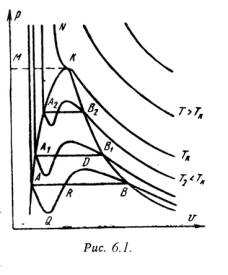
На PV – диаграмме (рис.6.1) показаны изотермы построенные по уравнению Ван-дер-Ваальса. Из кривых видно, что при сравнительно низких температурах имеются волнообразные участки. Чем выше температура, тем короче эти части кривых. Эти волнообразные кривые указывают на непрерывный переход от жидкого состояния в парообразное при данной температуре. Точка А соответствует состоянии жидкости, точка В относится парообразному состоянии вещества.
В действительности переход из жидкого состояния в парообразное всегда происходит через двухфазное состояние вещества. При этом при данной температуре процесс перехода происходит также и при постоянном давлении. Этот действительный переход из жидкого состояния в парообразное изображается прямой линией АВ.
Практически для особо чистых веществ возможно осуществление участков волнообразной кривой AQ и DB. В первом случае имеют место неустойчивые состояния перегретой жидкости, а во втором – переохлажденного пара.
При определенной температуре изотерма уравнения Ван-дер-Ваальса не будет иметь волнообразного участка (точка К). Эту температуру называют критической. Если соединить точки А1, А2, А3 … и В1, В2, В3 . получим кривую похожую на параболу. Кривая АК называется нижней пограничной кривой и соответствует в состоянии кипения жидкости. Кривая КВ называется верхней пограничной кривой и соответствует состояния сухого насыщенного пара.
Таким образом, для реального вещества PV – диаграмму можно разбить на 3 области:
1 — область жидкого состояния, расположена левее нижней пограничной кривой;
2 — область двухфазных состояний (влажный пар), расположена между нижней и верхней пограничной кривой);
3 – область перегретого пара, расположена правее верхней пограничной кривой и выше критической точки. Условно область жидкости ограничивают сверху линией КМ – критическая изобара.
Критическую температуру Д.И.Менделеев называл абсолютной температурой кипения, при которой поверхностное натяжение в жидкости становится равным нулю, т.е. исчезает различие между жидкостью и парообразным состоянием вещества (насыщенным паром).
Связь между критическими параметрами и постоянными уравнения Ван-дер-Ваальса:
Уравнение Ван-дер-Ваальса при больших плотностях газа дает значительные ошибки. Кроме этого экспериментальным путем доказана, что коэффициенты а, b зависят от температуры и давления, причем эта зависимость очень сложная.
М.П.Вукалович и И.И.Новиков в 1939 г. предложили новое универсальное уравнение состояния реальных газов с учетом ассоциации и диссоциации их молекул, который имеет следующий вид:
(P + a/ n 2 )·( n – b) = R·T (1 – С/( n ·Т (3+2m)/2 ), (6.6)
С, m – постоянные, определяемые на основании опытных данных.
📺 Видео
Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

МКТ идеального газа. Уравнения состояния идеального газа | Физика, онлайн-форумСкачать

Уравнение состояния идеального газаСкачать

Эта тема ВСЕГДА встречается на экзамене ЦТ — Изопроцессы (Физика для чайников)Скачать

Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать

Подготовка к ЕГЭ по физике. Уравнение состояния идеального газа. Изопроцессы.Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Уравнение состояния идеального газаСкачать

Физика. 10 класс. Уравнение состояния идеального газа /23.11.2020/Скачать

Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Уравнение Ван-дер-Ваальса | Газы.Молекулярно-кинетическая теория | Химия (видео 8)Скачать

Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Идеальный и реальный газ | Газы.Молекулярно-кинетическая теория | Химия (видео 7)Скачать