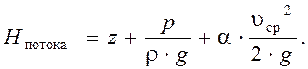- Энергетическая интерпретация уравнения Бернулли для установившегося движения
- Энергетическая интерпретация уравнения Бернулли
- Лекция 4
- 4.2. Геометрическая интерпретация уравнения Бернулли
- 4.3. Энергетическая интерпретация уравнения Бернулли
- 4.4. Уравнение Бернулли для потока реальной жидкости
- В энергетической интерпретации уравнения бернулли для установившегося движения невязкой
- Популярные тесты
- Преимущества
- Пользователям
- 📺 Видео
Видео:Закон БернуллиСкачать

Энергетическая интерпретация уравнения Бернулли для установившегося движения
Энергетическая интерпретация уравнения Бернулли для установившегося движения. Рассмотрим уравнение Бернулли для стационарного движения невязкой несжимаемой жидкости под действием силы тяжести и давления (4.13) 2 + п! Ре + У2 / 2§ копз!。 Где r-высота поперечного сечения элементарного потока на горизонтальной плоскости, называемой плоскостью сравнения. Эта высота легко дает ощущение energy. In дело в том, что когда плоскость сравнения является плоскостью потенциальной энергии нуля, то можно сказать, что потенциальная энергия mg передавалась при подъеме массы жидкости M на высоту r.
В результате r-Mrg / Mr представляет собой потенциальную энергию на единицу веса, а r называется удельной потенциальной энергией позиции. значение p / ryo также может иметь энергетическое значение. Рассмотрим основную струйку с площадью поперечного сечения u>0, давлением p, скоростью u. давление прикладывается к ПУ (.o. если частицы в этом сечении выходят за пределы расстояния u Людмила Фирмаль
- Эта работа относится к массе вытесненной жидкости ui1, Т объема. e.by деление ©кнана на исисиси, влияние давления на основе единицы веса жидкости Частица массой M и массой C = Mo, движущаяся со скоростью M и обладающая кинетической энергией mi2 / 2.Разделив эту кинетическую энергию на массу частиц, получим удельную кинетическую энергию (на единицу массы) U2 / 2d. Поэтому каждый член уравнения Бернулли представляет собой определенную потенциальную или кинетическую энергию. 86.
Сумма всех членов в уравнении Бернулли представляет собой сумму (потенциально положительное движение) энергии отношения жидкости в сечении потока. В приведенном выше примере удельная энергия была связана с удельным весом жидкости.Энергия также может быть отнесена к единицам массы[справочное уравнение(4.12)、(4.14)、(4.19)]или единичный объем. Общий потенциал и кинетическая энергия на единицу массы §Р+ п! п + » 72. Общая энергия на единицу объема §г + п + п » 72.
- Кроме того, если мы говорим об определенной энергии, то имеем в виду энергию, выделяемую на единицу веса. Удельная энергия определяется для произвольно выбранной горизонтальной опорной плоскости. Бернулли интерпретирует уравнение Бернулли для стационарного движения невязкой несжимаемой жидкости из энергетического положения следующим образом: в потенциальном движении и спиральном движении полная удельная энергия распределяется равномерно по всему потоку.
То есть она одинакова для любой пары точек в области, занимаемой движущейся жидкостью. При вихревых движениях (кроме спиралей) определенные энергии различаются в разных точках потока и постоянны только на каждой отдельной линии потока или линии вихря. Для Удельной (на единицу веса) энергии гидравлики используется термин напор. r + P’re + » 72 ^ = I.(4.22) Кроме того, r + p /p§называется пьезометрикой [(4.22) P = RPC case], или гидростатическим давлением. «2/25-скоростное давление.Я гидродинамическое давление.
Члены уравнения Бернулли имеют линейный размер, который можно интерпретировать как высоту.Р ■ геометрическая высота, или высота положения. p / p§ высота, соответствующая давлению, » 72 ^ высота скорости. Если вытянуть вертикальные сегменты r, p / p§и u2 / 2§из плоскости сравнения, то можно увидеть геометрическое положение ребер суммы этих сегментов. 。 4.3 его след представлен горизонтальной линией в верхней части, называемой линией давления или конкретной энергетической линией.
Таким образом, физический смысл уравнения Бернулли это закон сохранения энергии для движущейся жидкости. Людмила Фирмаль
- Если соединить концы отрезка r + p /ё, то получится пьезоэлектрический провод. Разница между высотой, соответствующей давлению, и высотой, соответствующей избыточному давлению Настройка Rat1re.Затем, в показанных 2 случаях (p или risb), как положение напорной головки, так и пьезометрическая линия являются rat/ p. Обычно под пьезометрической линией понимают линию, соединяющую концы сегмента, представляющего в общей сложности 2.
Пьезометрический наклон / n-это изменение пьезометрической головки r + p / p§ или изменение метки пьезометрической линии из-за общего случая, единицы длины. При движении потенциального шнека в данном потоке напорная поверхность равна 1, а при движении вихря каждая линия потока и вихревая линия имеют свою собственную напорную поверхность (след на рисунке-напорная линия). Линия пьезометра может быть уменьшена. Длина (r H ^




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Уравнение Бернулли гидравликаСкачать

Энергетическая интерпретация уравнения Бернулли
Выше было получено уравнение Бернулли с использованием энергетических характеристик жидкости. Суммарной энергетической характеристикой жидкости является её гидродинамический напор.
С физической точки зрения это отношение величины механической энергии к величине веса жидкости, которая этой энергией обладает. Таким образом, гидродинамический напор нужно понимать как энергию единицы веса жидкости. И для идеальной жидкости эта величина постоянна по длине. Таким образом, физический смысл уравнения Бернулли это закон сохранения энергии для движущейся жидкости
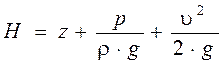
Физический смысл слагаемых, входящих в уравнение следующий:
ü z –удельная потенциальная энергия положения – энергия, обусловленная положением (высотой) единицы веса жидкости относительно плоскости сравнения (нулевого уровня), принимаемой за начало отсчета;
ü 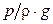
ü 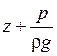
ü 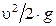
ü 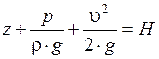
3.7Уравнение Бернулли для потока идеальной жидкости
Поток идеальной жидкости, как указывалось ранее, можно представить совокупностью элементарных струек жидкости. Скорости по сечению потока неодинаковы, причём в середине потока скорости наибольшие, а к периферии они уменьшаются (струйная модель потока) (рисунок 3.4). Это означает, что различные струйки в одном сечении имеют различные значения кинетической энергии. Отсюда следует, что кинетическая энергия, посчитанная с использованием скоростей элементарных струек υS, и кинетическая энергия, посчитанная с использованием значения средней скорости потока υ, будет иметь разные значения.
Вводят коэффициент кинетической энергии или коэффициента Кориолисаα.Смысл этого коэффициента заключается в отношении действительной кинетической энергии потока в определённом сечении к кинетической энергии в том же сечении потока, но при равномерном распределении скоростей. При равномерном распределении скоростей его значение равно единице, а при неравномерном – всегда больше единицы и для любого потока его значение находится в пределах от 1 до 2 и более.
Учитывая коэффициент кинетической энергии, приведём уравнение Бернулли для потока идеальной жидкости, которое примет вид:
Надо учесть, что в общем случае в разных сечениях потока коэффициент α будет иметь различные значения. При ламинарном режиме движения a=2; при развитом турбулентном режиме a=1,05 ¸ 1,1. Для большинства технических задач обычно принимается a=1.
3.8 Уравнение Бернулли для потока реальной (вязкой) жидкости
В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. По этой причине в процессе движения неизбежны потери энергии. Эта энергия, как и при любом трении, преобразуется в тепловую энергию. Из-за этих потерь энергия потока жидкости по длине потока, и в его направлении постоянно уменьшается. Т.е. напор потока Hпотока в направлении движения потока становится меньше. Если рассмотреть два соседних сечения 1-1 и 2-2, то потери гидродинамического напора Δh составят
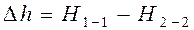
где 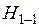
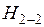
В этом случае уравнение Бернулли будет иметь вид
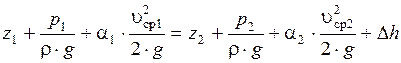
3.9Разность напоров и потери напора
Различие в применении терминов «разность напоров» и «потери напора»с одним и тем же обозначением Δh поясним на примерах.
Движение жидкости происходит только при наличии разности напоров(Δh = H1— H2), от точки с большим напором H1к точке с меньшим H2. Например, если два бака, заполненных водой до разных высотных отметок, соединить трубопроводом, то по нему начнётся перетекание в бак с меньшей отметкой уровня воды под влиянием разности напоров Δh, равной в этом случае разности отметок уровней воды в баках. При выравнивании уровней напоры в обоих баках становятся одинаковыми H1= H2, разность напоровΔh=0 и перетекание прекращается.
Потери напора Δh отражают потерю полной энергии потока при движении жидкости. Если в предыдущем примере на трубе установить задвижку и закрыть её, то движение воды прекратится и потерь напора не будет (Δh = 0), однако разность уровней воды будет создавать некоторую разность напоровΔh. После открывания задвижки вода вновь начнёт перетекать по трубе и общие потери напора в трубопроводе при движении из одного бака в другой будут равны разности напоров в баках Δh = H1— H2, то есть мы опять пришли к уравнению Бернулли.
Таким образом, «разность напоров»является причиной движения воды, а «потеря напора» — следствием. При установившемся движении жидкости они равны. Измеряются они в одних и тех же единицах СИ: метрах по высоте.
Обычно в гидравлических задачах при известных скорости 

3.10Кавитация
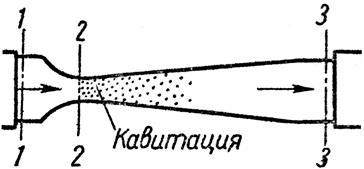
В некоторых случаях при движении жидкости в закрытых руслах происходят явления, связанные с изменением агрегатного состояния жидкости, т. с. с превращением ее в пар, а также с выделением из жидкости растворенных в ней газов. Например, при течении жидкости через местное сужение трубы (сечение 2-2) (рисунок 3.8) увеличивается скорость и падает давление согласно уравнению Бернулли
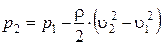
Рисунок 3.8 – Возникновение кавитации
Если абсолютное давление при этом достигает значения, равного давлению насыщенных паров этой жидкости при данной температуре, или давлению, при котором начинается выделение из нее растворенных газов, то в данном месте потока начинается интенсивное парообразование (кипение) и выделение газов. В расширяющейся части (сечение 3-3) скорость потока уменьшается, а давление возрастает, и выделение паров и газов прекращается; выделившиеся пары конденсируются, а газы постепенно вновь растворяются. Эта труба переменного сечения называется трубой Вентури, которая сначала плавно сужает поток, затем еще более плавно расширяет.
Это местное нарушение сплошности течения с образованием паровых и газовых пузырей (каверн), обусловленное местным падением давления в потоке, называется кавитацией.
Размеры зоны кавитации возрастают по мере увеличения скорости потока жидкости т. е. при увеличении давления в сечении 1-1, а следовательно, и расхода. Но давление в узком сечении 2-2 постоянно, потому, что постоянно давление насыщенных паров.
Кавитация сопровождается характерным шумом и вибрациями, а при длительном ее воздействии также эрозионным разрушением металлических стенок. Последнее объясняется тем. что конденсация пузырьков пара (и сжатие пузырьков газа) происходит со значительной скоростью, частицы жидкости, заполняющие полость конденсирующегося пузырька, устремляются к его центру и в момент схлопывания пузырька вызывают местные удары, т. е. значительное повышение давления в отдельных точках. Материал при кавитации разрушается не там, где выделяются пузырьки, а там, где они конденсируются. Это явление называется кавитационным износом.
При возникновении кавитации значительно увеличивается сопротивление трубопроводов и, следовательно, уменьшается их пропускная способность, потому что каверны уменьшают живые сечения потоков, скорость в которых резко возрастает.
Кавитация в обычных случаях является нежелательным явлением, и ее не следует допускать в трубопроводах и других элементах гидросистем. Она может возникать во всех местных гидравлических сопротивлениях, где поток претерпевает местное сужение с последующим расширением, например в кранах, вентилях, задвижках, диафрагмах, жиклерах и др. В отдельных случаях возникновение кавитации возможно также и без расширения потока вслед за его сужением, а также в трубах постоянного сечения при увеличении геометрической высоты и гидравлических потерь.
Кавитация возникает не только при движении жидкости в трубопроводе, но и при внешнем обтекании тел, в частности, на лопастях гребных винтов, рабочих колес насосов и гидравлических турбин.
Для оценки режима течения жидкости в каком-либо сечении потока вводят специальный критерий – число кавитации
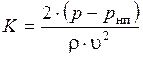
где p,υ — давление и средняя скорость течения жидкости в данном сечении потока.
3.11Моделирование гидродинамических явлений
Существует два различных метода моделирования:
— физическое моделирование, т.е. на модели воспроизводится изучаемое явление с сохранением его физических свойств;
— математическое моделирование, т.е. исследование натурных состояний или процессов выполняется путем изучения явлений, имеющих иное физическое содержание, но описываемое теми же математическими зависимостями.
Кроме того следует различать две разных категории моделей:
— воображаемые или мысленные, которые не полностью отражают действительность и могут быть также названы идеальными телами или процессами. Эти модели исследуются теоретически и результаты их исследования могут быть применены к реальности с помощью поправочных коэффициентов. Эти модели могут быть описаны чертежами, словами или математическими знаками.
— материальные, которые воспроизводят в определенном масштабе конструкции или процессы, имеющие место в действительности. Эти модели могут быть воспроизведены в лаборатории или в полевых условиях.
Оба видов моделей могут относиться и к математическому и физическому моделированию.
В дальнейшем понятие моделирование будет относиться к «материальному физическому» моделированию.
В процессе проектирования различных гидросистем, трубопроводов, гидротехнических сооружений, гидравлических и газовых систем нередко возникает необходимость не только математического, но и натурного моделирования. В таком случае необходимо, чтобы работа гидросистемы действующей модели соответствовала функционированию реального объекта. Это означает, что различные характеристики потоков жидкости, которые имеют место в модели и в реальной системе, должны описываться одинаковыми закономерностями, хотя их численные значения могут существенно различаться. В натурной модели они меньше (как правило) или больше (встречается реже), чем в действительности. Для этого необходимо иметь критерии, которые позволяли ли бы «масштабировать» реальную систему. Эти критерии устанавливаются в теории подобия потоков жидкости.
Представим себе две геометрически подобные фигуры (рисунок 3.9). Сходственными точками этих фигур называются точки, одинаково расположенные по отношению к границам этих фигур. Причем в сходственных точках фигур на частицы жидкости (сплошной среды) действуют силы одной физической природы.
Рисунок 3.9 – Подобные потоки жидкости
Гидродинамическое подобие— это подобие потоков несжимаемой жидкости, включающее в себя подобие геометрическое, кинематическое и динамическое.
Геометрическое подобие означает пропорциональность сходственных размеров и равенство соответствующих углов. В гидравлике под геометрическим подобием понимают подобие тех поверхностей, которые ограничивают потоки жидкости, т.е. подобие русел или трубопроводов, по которым течёт жидкость.
Например, для двух трубопроводов: 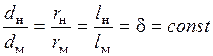
где δ – линейный масштаб подобия.
Кинематическоеподобие это подобие линий тока и пропорциональность сходственных скоростей. Это значит, что для кинематического подобия потоков требуется соблюдение геометрического подобия.
Например, для вращающегося движущегося тела
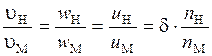
Т.о. кинематически подобные системы всегда будут геометрически подобными.
Динамическое подобие заключается в пропорциональности сил, действующих на сходственные элементы кинематически и геометрически подобных потоков, и равенство углов, характеризующих направление действия этих сил.
Т.е. можно сказать, что динамически подобными системами будут такие, для которых векторные поля сил, действующих на жидкость, образованы одноименными силами, причем эти поля будут геометрически подобными и одинаково ориентированы относительно границ систем.
В потоках жидкостей (в нашем случае в трубопроводах, в гидромашинах и т.д.) обычно действуют разные силы – силы давления, силы вязкого трения, силы тяжести, инерционные силы. Соблюдение пропорциональности всех сил, действующих в потоке, означает полное гидродинамическое подобие.
На практике полное гидродинамическое подобие достигается редко, поэтому обычно ограничиваются частичным (неполным) гидродинамическим подобием, при котором имеется пропорциональность лишь основных сил.
Записывается подобие следующим образом. Например, пропорциональность сил давления Р и сил трения Т, действующих в потоках I и II, можно записать в виде
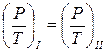
3.12Теория ламинарного и турбулентного движения жидкости
3.12.1Режимы течения жидкости в трубах
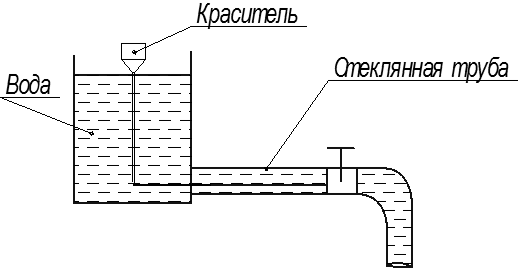
Еще в середине XIX века в результате опытов Гагена (1838 г.), Пуазейля (1841 г.) было установлено, что существуют два принципиально различных режима течения жидкости. Наиболее полно этот вопрос исследовал О.Рейнольдс (1883 г.). Различные режимы течения жидкости можно наблюдать вводя в поток подкрашивающую струйку красителя (рисунок 3.10).
Рисунок 3.10 – Схема установки О. Рейнольдса.
Замечено, что при небольшой скорости воды струйка красителя вытягивается в тонкую нить, которая, не размываясь, достигает конца трубы. Это свидетельствует о том, что пути частиц прямолинейны и параллельны друг другу.
Режим движения, при котором поток жидкости движется параллельно, скользящими друг относительно друга слоями или струйками, называется ламинарным. При этом режиме слои потока жидкости между собой не перемешиваются и движение происходит без пульсаций скорости. Ламинарный режим можно наблюдать в капиллярных трубках при движении вязких жидкостей типа нефти, мазута, сахарного сиропа и т. д.
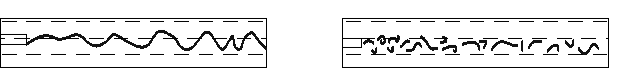
Если скорость воды в трубе увеличивать сверх определенного предела, то окрашенная струйка сначала приобретает волнообразное движение (рисунок 3.11), а затем начинает размываться, смешиваясь с водой. Такое неоднородное движение, при котором отдельные частицы жидкости движутся по беспорядочным, хаотическим траекториям, налагающимся на осредненное движение, называется турбулентным. В турбулентном потоке происходят пульсации скоростей, под действием которых частицы жидкости, движущиеся в главном (осевом) направлении, получают поперечные перемещения, приводящие к интенсивному перемешиванию потока по сечению.
Переход ламинарного режима в турбулентный происходит при определённой средней скорости течения υср, которая зависит от диаметра трубы и вязкости жидкости. Эту скорость называют критической и определяют по формуле
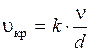
где 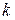
Т.е. изменение режима течения происходит при определённом соотношении между скоростью, диаметром и вязкостью ν
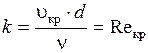
Полученное безразмерное число называется критическим числом Рейнольдса. С физической точки зрения число Рейнольдса есть отношение сил инерции потока к силам трения.
Опытным путём установлено, что критическое число Рейнольдса для круглых труб — 2320для круглых труб, а для других сечений 580.
Для определения режима движения в потоке надо найти фактическое число Рейнольдса Re , которое можно установить для любого потока по формуле
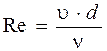
и сравнить его с критическим числом Reкр.
При движении жидкости в прямых круглых трубах на участках, достаточно удаленных от входа, и при отсутствии различных возмущающих условий установлено, что
¾ при Re 2320 – режим движения жидкости – турбулентный.
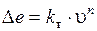
где kт и kл – коэффициенты пропорциональности (сопротивления трубопровода).
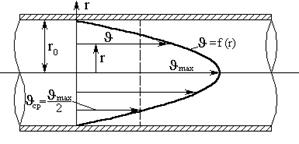
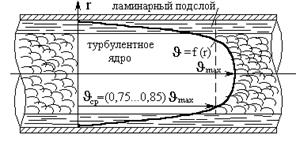
Различие между ламинарным и турбулентным режимами имеется также и в распределении скоростей в живом сечении потока.
При ламинарном режиме распределение скорости по сечению имеет параболический закон (рисунок 3.12, а); при турбулентном режиме закон распределения более сложный (рисунок 3.12, б).
Рисунок 3.12 – Распределение скорости в поперечном сечении трубы при ламинарном и турбулентном режиме движения жидкости.
Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Лекция 4
4.1. Уравнение Бернулли для жидкости
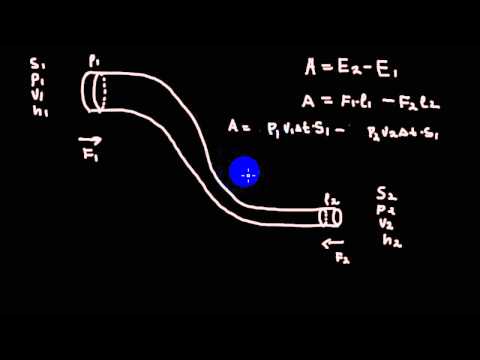
Рассмотрим поток жидкости, проходящий по трубопроводу переменного сечения (рис. 10). В первом сечении гидродинамический напор пусть равен H1. По ходу движения потока часть напора H1 необратимо потеряется из-за проявления сил внутреннего трения жидкости и во втором сечении напор уменьшится до H2 на величину потерь напора H.
Уравнение Бeрнýлли для жидкости в самом простейшем виде записывается так:
то есть это уравнение для двух сечений потока в направлении его течения, выраженное через гидродинамические напоры и отражающее закон сохранения энергии (часть энергии переходит в потери) при движении жидкости.
Уравнение Бeрнýлли в традиционной записи получим, если в последнем равенстве раскроем значения гидродинамических напоров H1 и H2 (м) :

Энергетический смысл уравнения Бeрнулли заключается в том, что оно отражает закон сохранения энергии: сумма потенциальной z+hp, кинетической v2/2g энергии и энергии потерь H остаётся неизменной во всех точках потока.
4.2. Геометрическая интерпретация уравнения Бернулли
Положение любой частицы жидкости относительно некоторой произвольной линии нулевого уровня 0-0 определяется вертикальной координатой Z. Для реальных гидравлических систем это может быть уровень, ниже которого жидкость из данной гидросистемы вытечь не может. Например, уровень пола цеха для станка или уровень подвала дома для домашнего водопровода.
· Как и в гидростатике, величину Z называют нивелирной высотой.
· Второе слагаемое — 
· Сумма первых двух членов уравнения 
· Третье слагаемое в уравнения Бернулли 
· Сумму всех трёх членов (высот) называют гидродинамическим или полным напором и, как уже было сказано, обозначают буквой Н.
 |
Все слагаемые уравнения Бернулли имеют размерность длины и их можно изобразить графически.
4.3. Энергетическая интерпретация уравнения Бернулли
Выше было получено уравнение Бернулли с использованием энергетических характеристик жидкости. Суммарной энергетической характеристикой жидкости является её гидродинамический напор.
С физической точки зрения это отношение величины механической энергии к величине веса жидкости, которая этой энергией обладает. Таким образом, гидродинамический напор нужно понимать как энергию единицы веса жидкости. И для идеальной жидкости эта величина постоянна по длине. Таким образом, физический смысл уравнения Бернулли это закон сохранения энергии для движущейся жидкости.

Физический смысл слагаемых, входящих в уравнение следующий:
· Z — потенциальная энергия единицы веса жидкости (удельная энергия) – энергия, обусловленная положением (высотой) единицы веса жидкости относительно плоскости сравнения (нулевого уровня), принимаемой за начало отсчета;
· 

· 
· 
· H — полная энергия единицы веса жидкости (полная удельная энергия).
4.4. Уравнение Бернулли для потока реальной жидкости
В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. По этой причине в процессе движения неизбежны потери энергии. Эта энергия, как и при любом трении, преобразуется в тепловую энергию. Из-за этих потерь энергия потока жидкости по длине потока, и в его направлении постоянно уменьшается. Т. е. напор потока Hпотока в направлении движения потока становится меньше. Если рассмотреть два соседних сечения 1-1 и 2-2, то потери гидродинамического напора Δh составят:

где H1-1— напор в первом сечении потока жидкости,
H2-2 — напор во втором сечении потока,
∆h — потерянный напор — энергия, потерянная каждой единицей веса движущейся жидкости на преодоление сопротивлений на пути потока от сечения 1-1 до сечения 2-2.
С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть
Индексами 1 и 2 обозначены характеристики потока в сечениях 1-1 и 2-2.
Если учесть, что характеристики потока V и α зависят от геометрии потока, которая для напорных потоков определяется геометрией трубопровода, понятно, что потери энергии (напора) в разных трубопроводах будут изменяться неодинаково. Показателем изменения напора потока является гидравлический уклон I, который характеризует потери напора на единице длины потока. Физический смысл гидравлического уклона – интенсивность рассеяния энергии по длине потока. Другими словами, величина I показывает, как быстро трубопровод поглощает энергию потока, протекающего в нём

Изменение энергии по длине потока удобно проследить на графиках. Из уравнения Бернулли для потока реальной жидкости (закона сохранения энергии) видно, что гидродинамическая линия для потока реальной жидкости (с одним источником энергии) всегда ниспадающая. То же справедливо и для пьезометрической линии, но только в случае равномерного движения, когда скоростной напор 
4.5. Разность напоров и потери напора
Различие в применении терминов «разность напоров» и «потери напора» с одним и тем же обозначениемH поясним на примерах.
Движение жидкости происходит только при наличии разности напоров (H = H1 — H2), от точки с бóльшим напором H1 к точке с меньшим H2. Например, если два бака, заполненных водой до разных высотных отметок, соединить трубопроводом, то по нему начнётся перетекание в бак с меньшей отметкой уровня воды под влиянием разности напоров H, равной в этом случае разности отметок уровней воды в баках. При выравнивании уровней напоры в обоих баках становятся одинаковыми H1 = H2 , разность напоров H=0 и перетекание прекращается.
Потери напора H отражают потерю полной энергии потока при движении жидкости. Если в предыдущем примере на трубе установить задвижку и закрыть её, то движение воды прекратится и потерь напора не будет (H = = 0), однако разность уровней воды будет создавать некоторую разность напоров H. После открывания задвижки вода вновь начнёт перетекать по трубе и общие потери напора в трубопроводе при движении из одного бака в другой будут равны разности напоров в баках H = H1 — H2 , то есть мы опять пришли к уравнению Бернулли.
Таким образом, «разность напоров» является причиной движения воды, а «потеря напора» — следствием. При установившемся движении жидкости они равны. Измеряются они в одних и тех же единицах СИ: метрах по высоте.
Обычно в гидравлических задачах при известных v или q определяемая величина H назывется потерей напора и, наоборот, при определении v или q известная H — разностью напоров.
4.6. Связь давления и скорости в потоке
Связь давления и скорости в потоке жидкости — обратная: если в каком-то месте потока скорость увеличивается, то давление здесь малó, и, наоборот, там, где скорости невелики, давление повышенное. Эту закономерность объясним на основе уравнения Бернýлли.
Рассмотрим работу водоструйного насоса (см. рис. 11). На подходе по нагнетательному трубопроводу 1 поток рабочей жидкости имеет относительно небольшую скорость v1 и высокое избыточное давление pизб1. Проходя через соплó 2, поток сужается, скорость его резко возрастает до v2. Для дальнейших рассуждений запишем уравнение Бернýлли так:

Здесь нет z1 и z2, так как труба горизонтальная, а величиной потерь напора DH» 0 пренебрегаем. Так как в правой части уравнения кинетическая составляющая энергии потока резко возросла из-за увеличения v2, то потенциальная составляющая, связанная с избыточным давлением после соплá pизб2, наоборот, уменьшится. Величину pизб2 можно выразить из этого уравнения и найти численное значение. Если pизб2 получается отрицательным, то, значит, возник вакуум (полное давление в струе стало меньше атмосферного). В последнем случае пьезометрическая линия опустится ниже отметки самой струи (см. рис 11).
Таким образом в струе рабочей жидкости после соплá образуется область пониженного давления или даже вакуум, что вызывает подсос транспортируемой жидкости по всасывающему трубопроводу 3 (см. рис. 11). Далее обе жидкости смешиваются в горловине 4 и транспортируются по отводящему трубопроводу 5.
Водоструйные насосы не имеют трущихся частей, в этом их преимущество перед механическими. По их принципу работают также эжекторы, гидроэлеваторы, насосы для создания вакуума.
Видео:Закон Бернулли и движение по инерцииСкачать

В энергетической интерпретации уравнения бернулли для установившегося движения невязкой
Ваша эрудиция на высоте, если осилите наш тест хотя бы на 8/11 — ТЕСТ
HTML-кодАнна Количество прохождений: 405 669 769 855 просмотров — 04 апреля 2020 Пройти тест
Лучший в мире тест на четкость зрения и мышления? Сможете пройти?
HTML-кодНикитин Константин Количество прохождений: 349 888 782 491 просмотров — 26 декабря 2016 Пройти тест
Блесните своей эрудицией, ответив на 70% вопросов верно
HTML-кодАндрей Количество прохождений: 554 672 1 475 221 просмотров — 26 февраля 2019 Пройти тест
Если вы наберете 11/12 в этом тесте на эрудицию, то такого начитанного и разностороннего человека еще поискать
HTML-кодАндрей Количество прохождений: 574 814 1 192 148 просмотров — 04 августа 2019 Пройти тест
Ваш словарный запас на высоком уровне, если наберете в нашем тесте хотя бы 8/11 — ТЕСТ
HTML-кодАнна Количество прохождений: 694 821 1 310 265 просмотров — 09 апреля 2020 Пройти тест
Тест, который проверит вашу эрудицию: где вы на шкале от 0 до 12?
HTML-кодАндрей Количество прохождений: 1 179 821 2 232 193 просмотров — 18 февраля 2019 Пройти тест
Тест на сленг СССР, который вы завалите, если не жили в то время
HTML-кодАндрей Количество прохождений: 304 725 495 414 просмотров — 27 февраля 2019 Пройти тест
Если вы закончите представленные 15 фраз, то вы настоящий интеллектуал!
HTML-кодАндрей Количество прохождений: 389 387 698 676 просмотров — 06 марта 2019 Пройти тест
Тест: Узнайте что говорит дата рождения о вашей Личности
HTML-кодНикитин Константин Количество прохождений: 1 142 788 2 247 862 просмотров — 26 декабря 2016 Пройти тест
Только те, кто росли в СССР, смогут без труда ответить на все вопросы нашего теста
HTML-кодАндрей Количество прохождений: 301 964 474 274 просмотров — 23 ноября 2018 Пройти тест
Не заглядывая в Гугл, сможете ответить хотя бы на половину вопросов этого теста?
HTML-кодАндрей Количество прохождений: 425 571 694 964 просмотров — 22 августа 2019 Пройти тест
Элементарный тест на логику и интеллект, который заваливает большинство взрослых. А вы наберете 15 из 15?
HTML-кодАндрей Количество прохождений: 353 887 654 618 просмотров — 07 августа 2019 Пройти тест
Тест на интеллект: Если наберете 9/9, то уровень вашего IQ точно выше среднего
HTML-кодАндрей Количество прохождений: 810 223 1 604 721 просмотров — 16 ноября 2019 Пройти тест
Сможете ответить на вопросы на общие знания, в которых стыдно сделать ошибку?
HTML-кодАндрей Количество прохождений: 302 918 497 362 просмотров — 24 декабря 2018 Пройти тест
Из какой страны вы душой?
HTML-кодКоклягина Полина Количество прохождений: 742 181 1 097 163 просмотров — 05 января 2017 Пройти тест
Главный тест на общие знания: насколько ты умён?
HTML-кодВсякие Научные Штуки Количество прохождений: 460 306 647 968 просмотров — 28 февраля 2019 Пройти тест
Сумеешь угадать фильм с одного кадра?
HTML-кодАндрей Количество прохождений: 290 552 535 968 просмотров — 15 июня 2018 Пройти тест
Сможете ли вы узнать 20 людей, определивших ход истории?
HTML-кодАндрей Количество прохождений: 658 821 1 075 950 просмотров — 12 февраля 2019 Пройти тест
Вы невероятно умны, если смогли пройти этот тест на 10 из 10
HTML-кодАндрей Количество прохождений: 403 606 722 373 просмотров — 21 февраля 2019 Пройти тест
Тест о животных: Угадай зверя по его носу
HTML-кодVyacheslaw Количество прохождений: 368 396 581 133 просмотров — 10 декабря 2018 Пройти тест
Подписывайтесь на наши странички! Обязательно делитесь с друзьями! Впереди много новых интересных тестов! Ежедневные добавления! Страницы: Яндекс Дзен, ВКонтакте, Одноклассники, Facebook
Популярные тесты
Ваша эрудиция на высоте, если осилите наш тест хотя бы на 8/11 — ТЕСТ
HTML-кодАнна Количество прохождений: 405 669 769 855 просмотров — 04 апреля 2020 Пройти тест
Лучший в мире тест на четкость зрения и мышления? Сможете пройти?
HTML-кодНикитин Константин Количество прохождений: 349 888 782 491 просмотров — 26 декабря 2016 Пройти тест
Блесните своей эрудицией, ответив на 70% вопросов верно
HTML-кодАндрей Количество прохождений: 554 672 1 475 221 просмотров — 26 февраля 2019 Пройти тест
Если вы наберете 11/12 в этом тесте на эрудицию, то такого начитанного и разностороннего человека еще поискать
HTML-кодАндрей Количество прохождений: 574 814 1 192 148 просмотров — 04 августа 2019 Пройти тест
Ваш словарный запас на высоком уровне, если наберете в нашем тесте хотя бы 8/11 — ТЕСТ
HTML-кодАнна Количество прохождений: 694 821 1 310 265 просмотров — 09 апреля 2020 Пройти тест
Тест, который проверит вашу эрудицию: где вы на шкале от 0 до 12?
HTML-кодАндрей Количество прохождений: 1 179 821 2 232 193 просмотров — 18 февраля 2019 Пройти тест
Тест на сленг СССР, который вы завалите, если не жили в то время
HTML-кодАндрей Количество прохождений: 304 725 495 414 просмотров — 27 февраля 2019 Пройти тест
Если вы закончите представленные 15 фраз, то вы настоящий интеллектуал!
HTML-кодАндрей Количество прохождений: 389 387 698 676 просмотров — 06 марта 2019 Пройти тест
Тест: Узнайте что говорит дата рождения о вашей Личности
HTML-кодНикитин Константин Количество прохождений: 1 142 788 2 247 862 просмотров — 26 декабря 2016 Пройти тест
Только те, кто росли в СССР, смогут без труда ответить на все вопросы нашего теста
HTML-кодАндрей Количество прохождений: 301 964 474 274 просмотров — 23 ноября 2018 Пройти тест
Не заглядывая в Гугл, сможете ответить хотя бы на половину вопросов этого теста?
HTML-кодАндрей Количество прохождений: 425 571 694 964 просмотров — 22 августа 2019 Пройти тест
Элементарный тест на логику и интеллект, который заваливает большинство взрослых. А вы наберете 15 из 15?
HTML-кодАндрей Количество прохождений: 353 887 654 618 просмотров — 07 августа 2019 Пройти тест
Тест на интеллект: Если наберете 9/9, то уровень вашего IQ точно выше среднего
HTML-кодАндрей Количество прохождений: 810 223 1 604 721 просмотров — 16 ноября 2019 Пройти тест
Сможете ответить на вопросы на общие знания, в которых стыдно сделать ошибку?
HTML-кодАндрей Количество прохождений: 302 918 497 362 просмотров — 24 декабря 2018 Пройти тест
Из какой страны вы душой?
HTML-кодКоклягина Полина Количество прохождений: 742 181 1 097 163 просмотров — 05 января 2017 Пройти тест
Главный тест на общие знания: насколько ты умён?
HTML-кодВсякие Научные Штуки Количество прохождений: 460 306 647 968 просмотров — 28 февраля 2019 Пройти тест
Сумеешь угадать фильм с одного кадра?
HTML-кодАндрей Количество прохождений: 290 552 535 968 просмотров — 15 июня 2018 Пройти тест
Сможете ли вы узнать 20 людей, определивших ход истории?
HTML-кодАндрей Количество прохождений: 658 821 1 075 950 просмотров — 12 февраля 2019 Пройти тест
Вы невероятно умны, если смогли пройти этот тест на 10 из 10
HTML-кодАндрей Количество прохождений: 403 606 722 373 просмотров — 21 февраля 2019 Пройти тест
Тест о животных: Угадай зверя по его носу
HTML-кодVyacheslaw Количество прохождений: 368 396 581 133 просмотров — 10 декабря 2018 Пройти тест
Преимущества
Можете встраивать тесты на Ваш сайт. Тест показывается нашем и других сайтах. Гибкие настройки результатов. Возможность поделиться тестом и результатами. Лавинообразный («вирусный») трафик на тест. Русскоязычная аудитория. Без рекламы!
Создавайте тесты онлайн, всё бесплатно. У нас можно бесплатно: создать тест онлайн для для учеников, друзей, сотрудников, для вашего сайта, с ответами и результатами — Все Бесплатно!
Пользователям
Вам захотелось отдохнуть? Или просто приятно провести время? Выбирайте и проходите онлайн-тесты, делитесь результатом с друзьями. Проверьте, смогут они пройти также как Вы, или может лучше?
Конструктор Тестов ру — это огромное количество интересных и бесплатных тестов на сообразительность, IQ, зрение, знания правил дорожного движения, программирования и многое другое. Если Вам понравилось, обязательно поделитесь со своими друзьями в социальных сетях или просто ссылкой. А еще Вы можете легко создать свой тест и его будут проходить десятки тысяч людей.
Внимание! Наши тесты не претендуют на достоверность – не стоит относиться к ним слишком серьезно!
📺 Видео
Закон БернуллиСкачать

Урок 134. Применения уравнения Бернулли (ч.1)Скачать

Уравнение Бернулли. Диаграмма Бернулли.Скачать

Уравнение Бернулли для потока жидкостиСкачать

Уравнение БернуллиСкачать

Галилео. Эксперимент. Закон БернуллиСкачать

10. Уравнения БернуллиСкачать

Уравнение Бернулли и его приложения | Гидродинамика, ГидравликаСкачать

Уравнение БернуллиСкачать

Якута А. А. - Механика - Гидростатика. Уравнение Бернулли. Формула ПуайзеляСкачать

Уравнение Бернулли. Практическая часть. 10 класс.Скачать

Уравнение Бернулли Метод БернуллиСкачать

Вывод уравнения неразрывности - Лекция 1Скачать

Основы гидродинамики и аэродинамики | условие неразрывностиСкачать

Основы гидродинамики и аэродинамики | уравнение БернуллиСкачать
Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать