В длинном шнуре распространяется гармоническая поперечная волна которая описывается уравнением (3 видео)

Упругие волны

116. Определите разность фаз Δφ колебаний двух точек, лежащих на луче и друг от друга на расстоянии Δl = 1 м, если длина волны λ = 0,5 м.

117. Две точки лежат на луче и находятся от источника колебаний на расстоянии x₁ = 4 м и x₂ = 7 м. Период колебаний T = 20 мс и скорость v распространения волны равна 300 м/с. Определите разность фаз колебаний этих точек.

118. Волна распространяется в упругой среде со скоростью v = 150 м/с. Определите частоту ν колебаний, если минимальное расстояние Δx между точками среды, фазы колебаний которых противоположны, равно 0,75 м.

119. Определите длину волны λ, если числовое значение волнового вектора k равно 0,02512 см -1 .

120. Звуковые колебания с частотой ν = 450 Гц и амплитудой А = 0,3 мм распространяются в упругой среде. Длина волны λ = 80 см. Определите: 1) скорость распространения волн; 2) максимальную скорость частиц среды.

121. Плоская синусоидальная волна распространяется вдоль прямой, совпадающей с положительным направлением оси x в среде, не поглощающей энергию, со скоростью v = 10 м/с. Две точки, находящиеся на этой прямой на расстоянии x₁ = 7 м и x₂ = 10 м от источника колебаний, колеблются с разностью фаз Δφ = Зπ/5 . Амплитуда волны А = 5 см. Определите: 1) длину волны λ; 2) уравнение волны; 3) смещение E₂ второй точки в момент времени t₂ = 2 с.

122. Поперечная волна распространяется вдоль упругого шнура со скоростью v = 10 м/с. Амплитуда колебаний точек шнура A = 5 см, а период колебаний T = 1 с. Запишите уравнение волны и определите: 1) длину волны; 2) фазу колебаний, смещение, скорость и ускорение точки, расположенной на расстоянии x₁ = 9 м от источника колебаний в момент времени t₁ = 2,5 с.

124. Выведите связь между групповой и фазовой скоростями.

126. Определите групповую скорость для частоты ν = 800 Гц, если фазовая скорость задается выражением v = a₀ / корень(v+b), где a₀ = 24 м*с -3/2 , b = 100 Гц.

127. Два когерентных источника колеблются в одинаковых фазах с частотой ν = 400 Гц. Скорость распространения колебаний в среде v = 1 км/с. Определите, при какой наименьшей разности хода, не равной нулю, будет наблюдаться: 1) максимальное усиление колебаний; 2) максимальное ослабление колебаний.

128. Два когерентных источника посылают поперечные волны в одинаковых фазах. Периоды колебаний Т = 0,2 с, скорость распространения волн в среде v = 800 м/с. Определите, при какой разности хода в случае наложения волн будет наблюдаться: 1) ослабление колебаний; 2) усиление колебаний.

130. Два динамика расположены на расстоянии d = 0,5 м друг от друга и воспроизводят один и тот же музыкальный тон на частоте ν = 1500 Гц. Приемник находится на расстоянии l = 4 м от центра динамиков. Принимая скорость звука v = 340 м/с, определите, на какое расстояние от центральной линии параллельно динамикам надо отодвинуть приемник, чтобы он зафиксировал первый интерференционный минимум.

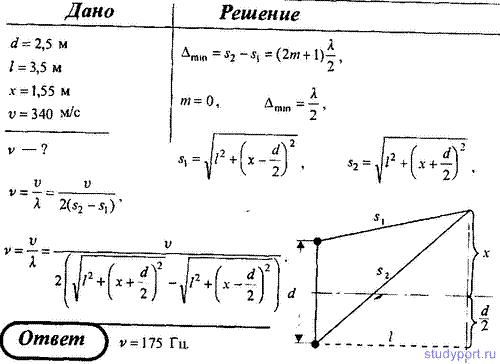
131. Два динамика расположены на расстоянии d = 2,5 м друг от друга и воспроизводят один и тот же музыкальный тон на определенной частоте, который регистрируется приемником, находящимся на расстоянии l = 3,5 м от центра динамиков. Если приемник передвинуть от центральной линии параллельно динамикам на расстояние x = 1,55 м, то он фиксирует первый интерференционный минимум. Скорость звука v = 340 м/с. Определите частоту звука.

134. Определите длину бегущей волны λ, если расстояние Δl между первым и четвертым узлами стоячей волны равно 30 см.

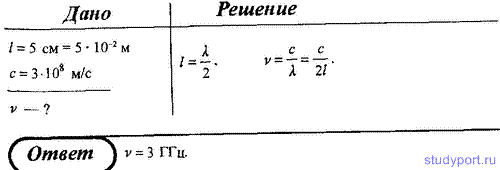
135. СВЧ-генератор излучает в положительном направлении оси x плоские электромагнитные волны, которые затем отражаются обратно. Точки M₁ и M₂ соответствуют положениям двух соседних минимумов интенсивности и отстоят друг от друга на расстоянии l = 5 см. Определите частоту микроволнового генератора.

136. Один конец упругого стержня соединен с источником гармонических колебаний, подчиняющихся закону ε = A cos ωt, а другой его конец жестко закреплен. Учитывая, что отражение в месте закрепления стержня происходит от менее плотной среды, определите характер колебаний в любой точке стержня.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Содержание

Падающая гармоническая поперечная волна (см. рис. 250) описывается уравнением [А — амплитуда, со — частота, v — скорость волны].
Ваш ответ
решение вопроса
Похожие вопросы
§ 4.5. Уравнение бегущей волны
🌟 Видео

Видео:Распространение колебаний в среде. Волны | Физика 9 класс #28 | ИнфоурокСкачать

Падающая гармоническая поперечная волна (см. рис. 250) описывается уравнением [А — амплитуда, со — частота, v — скорость волны].

Видео:Урок 370. Механические волны. Математическое описание бегущей волныСкачать

Ваш ответ

Видео:Якута А. А. - Механика - Волновое уравнение. Механические волны. Скорость распространения волнСкачать

решение вопроса

Видео:Тема 6. Распространение колебаний в упругой среде. Волны. Частота, длина, скорость распространенияСкачать

§ 4.5. Уравнение бегущей волны

Ось X направим вдоль шнура, а начало отсчета свяжем с левым концом шнура (см. рис. 4.11). Смещение любой колеблющейся точки шнура от положения равновесия обозначим буквой S. Для описания волнового процесса необходимо знать значение S в любой точке шнура в любой момент времени, а следовательно, знать вид функции s = s(x, t).

Заставим конец шнура (точка х = 0) соверпгать гармонические колебания с частотой ω. Колебания этой точки будут происходить по закону

если начальную фазу колебаний считать равной нулю. Здесь s_m — амплитуда колебаний (рис. 4.14, а).

Колебания распространяются вдоль шнура (оси X) со скоростью v и в произвольную точку шнура с координатой х придут спустя время

Эта точка также начнет совершать гармонические колебания с частотой ω, но с запаздыванием на время τ (рис. 4.14, б). Если пренебречь затуханием волны по мере ее распространения, то колебания в точке х будут происходить с той же амплитудой s_m, но с другой фазой:

Это и есть уравнение бегущей волны*, распространяющ;ей-ся в положительном направлении оси X. В случае, когда начальная фаза колебаний в точке x = 0 равна не нулю, а произвольной величине φ₀, уравнение бегуньей волны запишется так:

Амплитуда колебаний s_m называется амплитудой волны. Величину, стоящую под знаком синуса, называют фазой волны. В общем случае фаза волны равна:

Разумеется, вместо синуса при записи уравнения бегущей волны мы могли бы использовать и косинус. Замена синуса на косинус эквивалентна изменению начальной фазы на π/2.

Выражение (4,5.5) для фазы волны можно преобразовать, если выразить циклическую частоту колебаний ω через частоту v или период Т, а скорость волны v заменить ее значением согласно формуле (4.3.2). Для случая φ₀ = 0 получим:

Уравнение (4.5.3) бегущей гармонической волны примет при этом форму:

В этой форме записи отчетливо видно, что функция s(x, t) обладает периодичностью двоякого рода. Она периодична по времени при фиксированном х (период равен периоду колебаний Т, см. рис. 4.14) и периодична по пространству при фиксированном моменте времени (период равен длине волны λ, см. рис. 4.11). Это означает, что при замене t ⇒ t + Т или x ⇒ x + λ смещение s от положения равновесия согласно уравнению (4.5.7) остается одним и тем же.

Итак, в бегущей волне все точки среды (участки шнура) совершают вынужденные колебания с одним и тем же периодом, но с различными фазами. Две точки с координатами х₁ и х₂ имеют разность фаз

При x₂ — х₁ = λ, разность фаз равна 2π. Точки колеблются синфазно. Если х₂ — х₁ = λ/2. О колебания происходят в противофазе.

Надо отметить, что строго гармонических волн не существует. Из-за неизбежных потерь механической энергии амплитуда колебаний постепенно уменьшается по мере распространения волны от источника возбуждения колебаний. Можно приближенно говорить о гармонической волне в том случае, когда затухание бегущей волны на одной длине волны очень мало и по всей длине шнура укладывается много длин волн. Уравнение (4.5.3) описывает процессы не только в поперечной волне, но и в продольной, например в длинном упругом стержне. При этом s(x, t) по-прежнему имеет смысл смещения колеблющихся частей стержня от положения равновесия. Эти смещения в продольной волне происходят вдоль направления распространения волны (оси X).

* Волна называется бегущей по той причине, что, как мы увидим в следующем параграфе, существуют и стоячие волны, у которых максимумы и минимумы колебаний не перемещаются с течением времени.