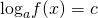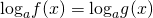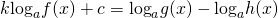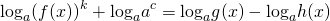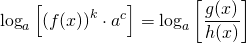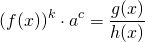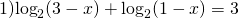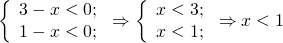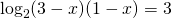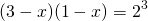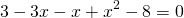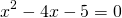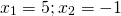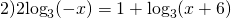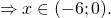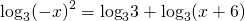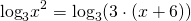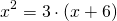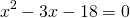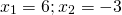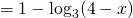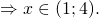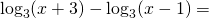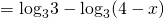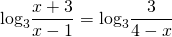Метод потенцирования [1, с. 125] – это один из методов решения уравнений. В этой статье мы всесторонне разберем этот метод. Сначала скажем, для решения каких уравнений он применяется. Дальше вникнем в суть метода потенцирования и дадим его обоснование. После этого запишем алгоритм решения уравнений методом потенцирования. Наконец, проанализируем решения нескольких характерных уравнений.
Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать

Когда применяется метод потенцирования
Метод потенцирования применяется для решения логарифмических уравнений, обе части которых представляют собой логарифмы по одинаковым основаниям. Например, применение метода потенцирования позволяет справиться с уравнениями log2(x−1)=log2(3·x−7) , и т.п. К методу потенцирования можно прибегать и в случаях, когда в основаниях логарифмов находятся не числа, а одинаковые выражения с переменными. Например, логарифмическое уравнение logx+4(x 2 −1)=logx+4(5−x) вполне можно решать методом потенцирования.
Видео:Логарифмические уравнения - Как решать методом потенцированияСкачать

Суть метода потенцирования
Суть метода потенцирования состоит в нахождении решения заданного уравнения посредством решения уравнения, полученного из исходного уравнения путем его почленного потенцирования, на области допустимых значений для исходного уравнения.
Не помешает пояснить, что такое почленное потенцирование. Напомним, что потенцирование заключается в восстановлении выражения по его логарифму. Поэтому, под почленным потенцированием уравнения logh(x)f(x)=logh(x)g(x) обычно понимают следующую последовательность преобразований уравнения:
которую обычно сокращают до , осуществляя первое преобразование в уме.
Проиллюстрируем суть метода потенцирования. Для этого обратимся к примеру: решение уравнения log2(x−1)=log2(3·x−7) методом потенцирования подразумевает переход к решению уравнения x−1=3·x−7 на ОДЗ для исходного логарифмического уравнения.
Видео:Логарифмические уравнения. 11 класс.Скачать

Обоснование метода
Метод потенцирования предполагает переход от уравнения logh(x)f(x)=logh(x)g(x) к сравнительно простому уравнению f(x)=g(x) . Но почему мы можем осуществлять такой переход, и каким является полученное уравнение, равносильным уравнением или уравнением-следствием? Ответы на эти вопросы дает следующее утверждение:
Почленное потенцирование уравнения в общем случае дает уравнение-следствие.
В первую очередь докажем, что любой корень уравнения logh(x)f(x)=logh(x)g(x) является корнем уравнения f(x)=g(x) .
Пусть x0 — корень уравнения logh(x)f(x)=logh(x)g(x) . Значит logh(x0)f(x0)=logh(x0)g(x0) — верное числовое равенство. Также из того, что x0 – корень уравнения logh(x)f(x)=logh(x)g(x) следует, что x0 принадлежит ОДЗ для этого уравнения, откуда вытекает, что h(x0)>0 и h(x0)≠1 . При этом известно, что две степени одного и того же положительного и отличного от единицы числа равны тогда и только тогда, когда равны показатели этих степеней (см. свойства степеней). Следовательно, (h(x0)) logh(x0)f(x0) =(h(x0)) logh(x0)g(x0) – верное числовое равенство. А основное логарифмическое тождество позволяет переписать его в виде f(x0)=g(x0) . Полученное равенство означает, что x0 – корень уравнения f(x)=g(x) .
Теперь докажем, что уравнение f(x)=g(x) может иметь корни, посторонние для уравнения logh(x)f(x)=logh(x)g(x) . На этом доказательство будет закончено. Для этого достаточно одного примера. В качестве такого примера приведем уравнение –x 2 +5·x+3=x 2 , которое получается в результате почленного потенцирования уравнения logx−1(–x 2 +5·x+3)=logx−1x 2 . Число −1/2 является корнем уравнения –x 2 +5·x+3=x 2 , но −1/2 – посторонний корень уравнения logx−1(–x 2 +5·x+3)=logx−1x 2 .
Остается обговорить, из-за чего при потенцировании обеих частей уравнения могут появляться посторонние корни. При переходе от уравнения logh(x)f(x)=logh(x)g(x) к уравнению f(x)=g(x) пропадают ограничения на значения переменной, связанные с логарифмами. Из-за этого может расшириться ОДЗ. А из-за расширения ОДЗ могут появиться посторонние корни. Других причин появления посторонних корней при потенцировании уравнения нет. Из этого следует, что при решении уравнений методом потенцирования отсеивание посторонних корней можно проводить с опорой на ОДЗ.
Видео:Проще простого! Как решить Логарифмическое Уравнение?Скачать

Алгоритм решения уравнений методом потенцирования
Информация предыдущих пунктов позволяет записать алгоритм решения уравнений методом потенцирования.
Чтобы решить уравнение методом потенцирования, надо
- Выполнить почленное потенцирование уравнения, то есть, перейти от уравнения logh(x)f(x)=logh(x)g(x) к уравнению f(x)=g(x) .
- Решить полученное уравнение.
- Если оно не имеет корней, то исходное уравнение тоже не имеет корней.
- Если оно имеет корни, то перейти к следующему шагу.
- Взять корни, принадлежащие условиям ОДЗ для исходного уравнения, или провести отсеивание посторонних корней любым другим способом.
Видео:Решение логарифмических уравнений ПРИМЕР #37 Метод логарифмированияСкачать

Примеры с решениями
Решение уравнений методом потенцирования обычно проводится в три этапа: проводится потенцирование уравнения, решается полученное уравнение, берутся все корни, удовлетворяющие условиям ОДЗ для исходного уравнения, остальные корни отбрасываются как посторонние. Давайте разберем пример решения уравнения методом потенцирования.
Решите уравнение методом потенцирования
Левая и правая части заданного уравнения представляют собой логарифмы по одинаковым основаниям 10 . Это позволяет нам использовать метод потенцирования для решения уравнения. Первое, что нам надо сделать по методу потенцирования, — это провести потенцирование уравнения:
Почленное потенцирование уравнения привело нас к рациональному уравнению . Теперь нам надо решить полученное уравнение:
Таким образом, уравнение имеет два корня x1=−1 и x2=3 .
Остается пройти последний шаг алгоритма решения уравнений методом потенцирования – отсеять посторонние корни. В нашем случае это удобно сделать по условиям ОДЗ для исходного уравнения . Для этого уравнения ОДЗ определяется системой . Корень x1=−1 не удовлетворяет записанной системе ( ), значит, является посторонним корнем уравнения . А x2=3 удовлетворяет ей ( ), значит, является корнем решаемого уравнения .
На этом решение уравнения методом потенцирования завершено. Уравнение имеет один корень 3 .
Для полноты картины стоит рассмотреть, как проводится потенцирование уравнений, когда в основаниях логарифмов находятся одинаковые выражения с переменными. Вот соответствующий пример с подробным решением.
Решите уравнение logx−1(–x 2 +5·x+3)=logx−1x 2
Перед нами логарифмическое уравнение. Части этого уравнения представляют собой логарифмы, в основаниях этих логарифмов находятся одинаковые выражения с переменной. Для решения подобных логарифмических уравнений подходит метод потенцирования.
Решение уравнений методом потенцирования проводится следующим образом:
- во-первых, выполняется почленное потенцирование уравнения,
- во-вторых, решается полученное уравнение,
- и, в-третьих, отсеиваются корни, посторонние для исходного уравнения.
Начинаем с потенцирования уравнения:
Полученное в результате потенцирования уравнение сводится к квадратному уравнению 2·x 2 −5·x−3=0 . Решаем его через дискриминант:
Остается пройти последний шаг метода потенцирования – отсеять посторонние корни. При решении уравнений методом потенцирования отсеивание посторонних корней обычно проводится по условиям ОДЗ. В нашем случае область допустимых значений для исходного уравнения logx−1(–x 2 +5·x+3)=logx−1x 2 определяется следующими условиями: –x 2 +5·x+3>0 , x 2 >0 , x−1>0 , x−1≠1 (выражения под знаками логарифмов должны быть положительными, а в основаниях логарифмов – положительными и отличными от единицы). Проверим, удовлетворяют ли найденные выше корни x1=−1/2 , x2=3 записанным условиям. Очевидно, x1=−1/2 не удовлетворяет условию x−1>0 , значит, x1=−1/2 – посторонний корень. А x2=3 удовлетворяет всем условиям ОДЗ ( ), следовательно, является корнем.
Таким образом, уравнение logx−1(–x 2 +5·x+3)=logx−1x 2 имеет единственный корень 3 .
В заключение этой статьи заметим, что почленное потенцирование уравнения logaf(x)=logag(x) с одинаковыми положительными и отличными от единицы числами в основаниях логарифмов ( a>0 и a≠1 ), дает такой же результат, что и освобождение от внешней функции: и в том, и в другом случае уравнение logaf(x)=logag(x) заменяется уравнением f(x)=g(x) .
Видео:Решение логарифмических уравнений #shortsСкачать

Урок-лекция по теме «Логарифмические уравнения. Основные методы их решения»
Презентация к уроку
В моём календарно-тематическом планировании на тему “Логарифмические уравнения” отводится 3 часа. Я их разбиваю следующим образом:
1 возможный вариант:
1 урок — лекция “Логарифмические уравнения. Основные методы их решения”. В конце лекции задаю блок уравнений обязательного уровня.
2 урок – решение уравнений различного типа и сложности (это зависит от уровня математической подготовки класса, использую индивидуальный подход).
3 урок – решение уравнений и зачётная работа с само- и взаимопроверкой, а также проверкой учителем.
2 возможный вариант:
1 урок — лекция “Логарифмические уравнения. Основные методы их решения”, но только два метода – на основании определения и потенцирования. Решение уравнений на применение этих методов.
2 урок – лекция “Логарифмические уравнения. Основные методы их решения”, два других метода – подстановки и логарифмирования. Решение уравнений на применение этих методов.
3 урок – решение уравнений и зачётная работа с само- и взаимопроверкой, а также проверкой учителем.
Вариант подачи темы зависит от подготовленности класса.
Лекция “Логарифмические уравнения. Основные методы их решения”.
Эпиграфом своей сегодняшней лекции я привожу слова Ричарда Олдингтона (1892 – 1962гг., английский поэт, прозаик, критик): “Ничему тому, что важно знать, научить нельзя, — всё, что может сделать учитель, это указать дорожки”.
А так же – русскую народную пословицу: “Кто говорит – тот сеет, кто слушает – тот собирает”.
В самом начале моей лекции я хотела бы обратить ваше внимание на следующее. При решении логарифмических уравнений применяют преобразования, которые не приводят к потере корней, но могут привести к приобретению посторонних корней. Поэтому проверка каждого из полученных корней обязательна, если нет уверенности в равносильности уравнений. Здесь возможны два подхода:
Проверка путём подстановки полученных решений в исходное уравнение.
Нахождение области допустимых значений уравнения (ОДЗ). Тогда корнями могут быть только те числа, которые принадлежат этой области.
В своей лекции я буду использовать оба этих подхода, а ваше право уже самим выбирать, какой лично вам больше нравится. Следует отметить, что при решении логарифмических неравенств возможен только один из них: ОДЗ!
Основные методы решения логарифмических уравнений.
Уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением.
Решение логарифмических уравнений на основании определения логарифма.
Определение логарифма: Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести основание а, чтобы получить число b. Т. е.
Таким образом, применяя его к нашей теме, мы получим следующее:

Пример 1:
Число 16 удовлетворяет ОДЗ, значит 16 – корень исходного уравнения.
Пример 2:
Проверка: 

Пример 3:
По определению логарифма 
Ответ:
А сейчас мы рассмотрим пример, в котором в основании логарифма уже не число, а выражение, содержащее переменную. Т. е. уравнение будет иметь вид 

Пример 4:
ОДЗ:
С учётом ОДЗ получим, что решением данного уравнения является число 2.
Как мы видим, наличие выражения с переменной в основании влияет лишь на ОДЗ, а не на ход рассуждений. Кроме того, данное уравнение можно решать, не прибегая к нахождению ОДЗ, а просто в конце выполнить проверку.
Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их.

Пример 5:




Значит, только число 1 является решением исходного уравнения.
Если же в основании – выражение с переменной, то рассуждения не меняем! В этом случае уравнение будет иметь вид

И пример такого уравнения можно разобрать на предыдущем примере 5.
Пример 6:




Значит, только число 1 является решением исходного уравнения.
ОДЗ для данного уравнения выглядит следующим образом:
Мы видим, что в этом уравнении рациональнее выполнить проверку, а не искать ОДЗ. Но ещё раз повторюсь, что при решении неравенств ОДЗ находить придётся ОБЯЗАТЕЛЬНО.
Рассмотрим пример, который, на первый взгляд, не может относиться к данному типу уравнений.
Пример7:
Сделаем замену 




Проверка: 

Замечу, что часто перед применением какого-либо метода решений, необходимо преобразовать уравнение, применив различные свойства логарифмов. Предыдущий пример, тому подтверждение.
Данный метод мы достаточно часто встречаем в математике, вспомните тригонометрические или показательные уравнения. Поэтому применение его при решении логарифмических уравнений я вам покажу на примере.
Пример 8: 
В этом уравнении рациональней найти ОДЗ:
Пусть 

Значит 

2)
Мы видим, что оба корня удовлетворяют ОДЗ, значит оба числа являются решениями исходного уравнения.
Ответ:
Если в основании логарифма лежит выражение с переменной, то уравнение в общем виде будет выглядеть следующим образом:

И опять, вы сами выбираете: ОДЗ или проверка.
Пример 9: 
ОДЗ:
Приведём логарифмы к одному основанию – 7, пользуясь свойством перехода к новому основанию 



 | или |  . . |
 |  | |
 |  |
Оба числа удовлетворяют ОДЗ.
Ответ:
Данный метод является “обратным” методу потенцирования, т. е. мы от уравнения без логарифмов переходим к уравнению, их содержащему.

Этот метод обычно используется, если в уравнении есть показательные функции, логарифмы – в показателе. Рассмотрим этот метод на примере.
Пример 10:
ОДЗ:
Прологарифмируем обе части уравнения по основанию 3:


Выполним подстановку 
 | или |  . . |
 |  | |
 |  |
Оба числа удовлетворяют ОДЗ.
Этот пример показывает, что при решении логарифмических уравнений, возможна комбинация нескольких методов. А значит необходимо уметь пользоваться каждым из них. Научиться этому – теперь ваша задача.
Итак, сегодня мы с вами рассмотрели основные методы решения логарифмических уравнений:
- На основании определения логарифма.
- Метод потенцирования.
- Метод постановки.
- Метод логарифмирования.
Главным, по моему мнению, является метод, основанный на определении логарифма. Практически в каждом их других методов происходит “выход” на него. Кроме того, на примерах мы увидели, что все методы взаимосвязаны, в “чистом” виде при решении уравнений не используется ни один из них. Поэтому вам необходимо уметь пользоваться КАЖДЫМ!
Для отработки навыков решения логарифмических уравнений, я вам предлагаю следующее домашнее задание. Уравнения являются базовыми, т. е. решать их должен уметь решать каждый. Отмечу, что подборка сделана из открытого банка заданий для экзамена по математике ЕГЭ http://mathege.ru .
| № п/п | Уравнения | Комментарии (даётся для слабых учащихся) |
| 1 |  | Пользуясь определением |
| 2 |  | Пользуясь определением |
| 3 |  | Потенциирование |
| 4 |  | Потенциирование |
| 5 |  | Потенциирование |
| 6 |  | Потенциирование |
| 7 |  | Применить свойства логарифмов и затем потенциировать |
| 8 |  | Применить свойства логарифмов и затем потенциировать |
| 9 |  | Пользуясь определением |
| 10 |  | Пользуясь определением, выход на показательное уравнение |
| 11 |  | Показательное уравнение, выход на логарифмическое |
Замечание: домашнее задание распечатано на листах для каждого ученика.
Решение задач по теме “Логарифмические уравнения”. Зачёт.
Уравнения (примерные, зависит от математической подготовки учащихся).
Видео:11 класс, 17 урок, Логарифмические уравненияСкачать

Потенцирование
Потенцирование — это действие, заключающееся в нахождении числа по данному логарифму через логарифмы других чисел (нем. potenzieren — возводить в степень, от Potenz — степень).
При решении уравнений потенцированием выражения преобразовывают с помощью свойств логарифмов, приводя их к виду
Схематически логарифмическое уравнение, решаемое потенцированием, можно представить приблизительно так:
Решение начинаем с нахождения ОДЗ:
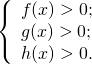
Затем преобразовываем выражение: число перед логарифмом вносим в показатель степени выражения, стоящего под знаком логарифма, а отдельно стоящее число представляем в виде логарифма по тому же основанию, что и остальные логарифмы:
От суммы логарифмов переходим к логарифму произведения, от разности — к логарифму частного:
Теперь приравниваем выражения, стоящие под знаками логарифмов
и решаем алгебраическое уравнение.
Рассмотрим примеры решения логарифмических уравнений потенцированием.
От суммы логарифмов переходим к логарифму произведения:
По определению логарифма
Первый корень не входит в ОДЗ.
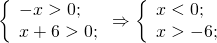
Число 2 вносим в показатель степени выражения, стоящего под знаком логарифма. Единицу представляем в виде логарифма по основанию 3
(-x)²=x². От суммы логарифмов переходим к логарифму произведения
Так как равны логарифмы с одинаковыми основаниями, можем приравнять выражения, стоящие под знаками логарифмов:
Первый корень не входит в ОДЗ.
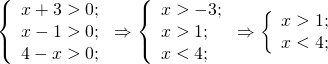
Единицу представляем в виде логарифма по основанию 3:
От разности логарифмов переходим к логарифму частного:
Приравниваем выражения, стоящие под знаками логарифмов:
📽️ Видео
84 людей этого не знают! Секретный способ решения Логарифмических УравненийСкачать

Решение логарифмических уравнений. Вебинар | МатематикаСкачать

Логарифмические уравнения. Часть 2 из 4. ПотенцированиеСкачать

✓ Как решать логарифмические уравнения и неравенства, не помня свойства логарифмов | Борис ТрушинСкачать

Алгебра 10 класс (Урок№27 - Логарифмические уравнения.)Скачать

Логарифмические уравнения. Видеоурок 18. Алгебра 10 классСкачать

Урок 7. Логарифмирование и потенцирование выражений.Скачать

Логарифм с нуля до уровня про. Уравнения, неравенства и параметр. Профильный ЕГЭСкачать

Подготовка к ЕГЭ #75. Решение логарифмических уравнений методом логарифмированияСкачать

Методы решения логарифмических уравненийСкачать

Логарифмирование и потенцирование.Taking the logarithm and potentiating.Скачать

Алгебра 11 класс Системы Логарифмических уравненийСкачать

ЕГЭ. Математика. Логарифмические уравнения, неравенства и их системы. ПрактикаСкачать