В чем сущность метода ньютона для решения систем нелинейных уравнений

В более общем случае мы имеем не одно уравнение (1), а систему нелинейных уравнений $$ begin tag f_i(x_1, x_2, ldots, x_n) = 0, quad i = 1, 2, ldots n. end $$ Обозначим через ( mathbf = (x_1, x_2, ldots, x_n) ) вектор неизвестных и определим вектор-функцию ( mathbf(mathbf) = (f_1(mathbf), f_2(mathbf), ldots, f_n(mathbf)) ). Тогда система (2) записывается в виде $$ begin tag mathbf(mathbf) = 0. end $$ Частным случаем (3) является уравнение (1) (( n = 1 )). Второй пример (3) — система линейных алгебраических уравнений, когда ( mathbf (mathbf) = A mathbf — mathbf ).

Видео:Методы решения систем нелинейных уравнений. Метод Ньютона. Численные методы. Лекция 14Скачать

Метод Ньютона

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Решение нелинейных уравнений

При итерационном решении уравнений (1), (3) задается некоторое начальное приближение, достаточно близкое к искомому решению ( x^* ). В одношаговых итерационных методах новое приближение ( x_ ) определяется по предыдущему приближению ( x_k ). Говорят, что итерационный метод сходится с линейной скоростью, если ( x_ — x^* = O(x_k — x^*) ) и итерационный метод имеет квадратичную сходимость, если ( x_ — x^* = O(x_k — x^*)^2 ).

В итерационном методе Ньютона (методе касательных) для нового приближения имеем $$ begin tag x_ = x_k + frac, quad k = 0, 1, ldots, end $$

Вычисления по (4) проводятся до тех пор, пока ( f(x_k) ) не станет близким к нулю. Более точно, до тех пор, пока ( |f_(x_k)| > varepsilon ), где ( varepsilon ) — малая величина.

Простейшая реализация метода Ньютона может выглядеть следующим образом:

Чтобы найти корень уравнения ( x^2 = 9 ) необходимо реализовать функции

Данная функция хорошо работает для приведенного примера. Однако, в общем случае могут возникать некоторые ошибки, которые нужно отлавливать. Например: пусть нужно решить уравнение ( tanh(x) = 0 ), точное решение которого ( x = 0 ). Если ( |x_0| leq 1.08 ), то метод сходится за шесть итераций.

Теперь зададим ( x_0 ) близким к ( 1.09 ). Возникнет переполнение

Возникнет деление на ноль, так как для ( x_7 = -126055892892.66042 ) значение ( tanh(x_7) ) при машинном округлении равно ( 1.0 ) и поэтому ( f^prime(x_7) = 1 — tanh(x_7)^2 ) становится равной нулю в знаменателе.

Проблема заключается в том, что при таком начальном приближении метод Ньютона расходится.

Еще один недостаток функции naive_Newton заключается в том, что функция f(x) вызывается в два раза больше, чем необходимо.

Учитывая выше сказанное реализуем функцию с учетом следующего:

1. обрабатывать деление на ноль
2. задавать максимальное число итераций в случае расходимости метода
3. убрать лишний вызов функции f(x)

Метод Ньютона сходится быстро, если начальное приближение близко к решению. Выбор начального приближение влияет не только на скорость сходимости, но и на сходимость вообще. Т.е. при неправильном выборе начального приближения метод Ньютона может расходиться. Неплохой стратегией в случае, когда начальное приближение далеко от точного решения, может быть использование нескольких итераций по методу бисекций, а затем использовать метод Ньютона.

При реализации метода Ньютона нужно знать аналитическое выражение для производной ( f^prime(x) ). Python содержит пакет SymPy, который можно использовать для создания функции dfdx . Для нашей задачи это можно реализовать следующим образом:

Видео:МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

Решение нелинейных систем

Идея метода Ньютона для приближенного решения системы (2) заключается в следующем: имея некоторое приближение ( pmb^ ), мы находим следующее приближение ( pmb^ ), аппроксимируя ( pmb(pmb^) ) линейным оператором и решая систему линейных алгебраических уравнений. Аппроксимируем нелинейную задачу ( pmb(pmb^) = 0 ) линейной $$ begin tag pmb(pmb^) + pmb(pmb^)(pmb^ — pmb^) = 0, end $$ где ( pmb(pmb^) ) — матрица Якоби (якобиан): $$ pmb(pmb^) = begin frac<partial f_1(pmb^)> & frac<partial f_1(pmb^)> & ldots & frac<partial f_1(pmb^)> \ frac<partial f_2(pmb^)> & frac<partial f_2(pmb^)> & ldots & frac<partial f_2(pmb^)> \ vdots & vdots & ldots & vdots \ frac<partial f_n(pmb^)> & frac<partial f_n(pmb^)> & ldots & frac<partial f_n(pmb^)> \ end $$ Уравнение (5) является линейной системой с матрицей коэффициентов ( pmb ) и вектором правой части ( -pmb(pmb^) ). Систему можно переписать в виде $$ pmb(pmb^)pmb = — pmb(pmb^), $$ где ( pmb = pmb^ — pmb^ ).

Таким образом, ( k )-я итерация метода Ньютона состоит из двух стадий:

1. Решается система линейных уравнений (СЛАУ) ( pmb(pmb^)pmb = -pmb(pmb^) ) относительно ( pmb ).

2. Находится значение вектора на следующей итерации ( pmb^ = pmb^ + pmb ).

Для решения СЛАУ можно использовать приближенные методы. Можно также использовать метод Гаусса. Пакет numpy содержит модуль linalg , основанный на известной библиотеке LAPACK, в которой реализованы методы линейной алгебры. Инструкция x = numpy.linalg.solve(A, b) решает систему ( Ax = b ) методом Гаусса, реализованным в библиотеке LAPACK.

Когда система нелинейных уравнений возникает при решении задач для нелинейных уравнений в частных производных, матрица Якоби часто бывает разреженной. В этом случае целесообразно использовать специальные методы для разреженных матриц или итерационные методы.

Можно также воспользоваться методами, реализованными для систем линейных уравнений.

Видео:Методы численного анализа - Метод Ньютона, секущих для решения систем нелинейных уравненийСкачать

5.1. Приближённое решение систем нелинейных уравнений. Метод Ньютона

Рассмотрим нелинейную систему уравнений

(5.1)

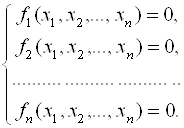
С действительными левыми частями. Систему (5.1) можно представить в матричном виде

(5.2)

Здесь приняты следующие обозначения:

— вектор аргументов, а — вектор – функция.

Для решения системы (5.2) воспользуемся методом последовательных приближений. Предположим, что найдено Р-ое приближение Xp = (X1(P), X2(P) , . Xn(P)) одного из изолированных корней X = (X1, X2, X3, . Xn) векторного уравнения (5.2). Тогда точный корень уравнения (5.2) можно представить в виде

(5.3)

Где — поправка (погрешность) корня на N – ом шаге.

Подставив выражение (5.3) в (5.2), получим

(5.4)

Предположим, что функция F(X) — непрерывно дифференцируема в некоторой выпуклой области, содержащей X и X(P). Тогда левую часть уравнения (5.4) разложим в ряд Тейлора по степеням малого вектора ε(P), ограничиваясь линейными членами:

, (5.5)

Или в развернутом виде:

(5.6)

Из анализа формул (5.5) и (5.6) следует, что под производной F¢(X) следует понимать матрицу Якоби системы функций F1 , F2, . Fn, относительно переменных X1, X2, X3, . Xn, то есть:

. (5.7)

Выражение (5.7) в краткой записи можно представить:

(5.8)

Выражение (5.6) представляет собой линейную систему относительно поправок (I = 1, 2, . N) с матрицей W(X), поэтому формула (5.5) может быть записана в следующем виде:

(5.9)

Отсюда, предполагая, что матрица W(X(P)) — неособенная, получим:

(5.10)

Теперь, подставив выражение (5.10) в формулу (5.3), окончательно получим:

(5.11)

Таким образом, получили вычислительную формулу (метод Ньютона), где в качестве нулевого приближения X(0) можно взять приближенное (грубое) значение искомого корня.

Пример 5.1. Рассмотрим применение метода Ньютона на примере системы двух нелинейных уравнений

(5.12)

Прежде чем разбирать конкретные шаги по решению системы (5.12), распишем в общем виде якобиан для системы из двух уравнений

Здесь A, B, C, D – функционалы от переменных X1, x2. Нас фактически интересует W-1. Пусть матрица W— неособенная, тогда обратная матрица вычисляется

Теперь вернемся к системе (5.12). Графическое решение этой системы дает две точки пересечения: М1 (1.4; -1.5) и М2 (3.4; 2.2). Зададим начальное приближение:

Видео:Алгоритмы С#. Метод Ньютона для решения систем уравненийСкачать

Численные методы решения нелинейных уравнений. Метод Ньютона для решения уравнений с одной переменной

Видео:Способы решения систем нелинейных уравнений. 9 класс.Скачать

Численные методы решения нелинейных уравнений. Метод Ньютона для решения уравнений с одной переменной

Метод Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643-1727), под именем которого и обрёл свою известность.

Метод был описан Исааком Ньютоном в рукописи De analysi per aequationes numero terminorum infinitas ( лат .О б анализе уравнениями бесконечных рядов), адресованной в 1669 году Барроу , и в работе De metodis fluxionum et serierum infinitarum ( лат.Метод флюксий и бесконечные ряды) или Geometria analytica ( лат.Аналитическая геометрия) в собраниях трудов Ньютона, которая была написана в 1671 году. Однако описание метода существенно отличалось от его нынешнего изложения: Ньютон применял свой метод исключительно к полиномам. Он вычислял не последовательные приближения x_n , а последовательность полиномов и в результате получал приближённое решение x.

Впервые метод был опубликован в трактате Алгебра Джона Валлиса в 1685 году, по просьбе которого он был кратко описан самим Ньютоном. В 1690 году Джозеф Рафсон опубликовал упрощённое описание в работе Analysis aequationum universalis (лат. Общий анализ уравнений). Рафсон рассматривал метод Ньютона как чисто алгебраический и ограничил его применение полиномами, однако при этом он описал метод на основе последовательных приближений x_n вместо более трудной для понимания последовательности полиномов, использованной Ньютоном.

Наконец, в 1740 году метод Ньютона был описан Томасом Симпсоном как итеративный метод первого порядка решения нелинейных уравнений с использованием производной в том виде, в котором он излагается здесь. В той же публикации Симпсон обобщил метод на случай системы из двух уравнений и отметил, что метод Ньютона также может быть применён для решения задач оптимизации путём нахождения нуля производной или градиента.

В соответствии с данным методом задача поиска корня функции сводится к задаче поиска точки пересечения с осью абсцисс касательной, построенной к графику функции .

Рис.1 . График изменение функции

Проведенная в любой точке касательная линия к графику функции определяется производной данной функции в рассматриваемой точке, которая в свою очередь определяется тангенсом угла α ( ). Точка пересечения касательной с осью абсцисс определяется исходя из следующего соотношения в прямоугольном треугольнике: тангенс угла в прямоугольном треугольнике определяется отношением противолежащего катета к прилежащему катету треугольнику. Таким образом, на каждом шаге строится касательная к графику функции в точке очередного приближения . Точка пересечения касательной с осью Ox будет являться следующей точкой приближения . В соответствии с рассматриваемым методом расчет приближенного значения корня на i -итерации производится по формуле:

Наклон прямой подстраивается на каждом шаге наилучшим образом, однако следует обратить внимание на то, что алгоритм не учитывает кривизну графика и следовательно в процессе расчета остается неизвестно в какую сторону может отклониться график.

Условием окончания итерационного процесса является выполнение следующего условия:

где ˗ допустимая погрешность определения корня.

Метод обладает квадратичной сходимостью. Квадратичная скорость сходимость означает, что число верных знаков в приближённом значении удваивается с каждой итерацией.

Математическое обоснование

Пусть дана вещественная функция , которая определена и непрерывна на рассматриваемом участке. Необходимо найти вещественный корень рассматриваемой функции.

Вывод уравнения основано на методе простых итераций, в соответствии с которым уравнение приводят к эквивалентному уравнению при любой функции . Введем понятие сжимающего отображения, которое определяется соотношением .

Для наилучшей сходимости метода в точке очередного приближения должно выполняться условие . Данное требование означает, что корень функции должен соответствовать экстремуму функции .

Производная сжимающего отображения определяется в следующем виде:

Выразим из данного выражение переменную при условии принятого ранее утверждения о том, что при необходимо обеспечить условие . В результате получим выражение для определения переменной :

С учетом этого сжимающая функция прием следующий вид:

Таким образом, алгоритм нахождения численного решения уравнения сводится к итерационной процедуре вычисления:

Алгоритм нахождения корня нелинейного уравнения по методу Ньютона для уравнения с одной переменной

1. Задать начальную точку приближенного значения корня функции , а также погрешность расчета (малое положительное число ) и начальный шаг итерации ( ).

2. Выполнить расчет приближенного значения корня функции в соответствии с формулой:

3. Проверяем приближенное значение корня на предмет заданной точности, в случае:

— если разность двух последовательных приближений станет меньше заданной точности , то итерационный процесс заканчивается.

— если разность двух последовательных приближений не достигает необходимой точности , то необходимо продолжить итерационный процесс и перейти к п.2 рассматриваемого алгоритма.

Пример решения уравнений

по методу Ньютона для уравнения с одной переменной

В качестве примера, рассмотрим решение нелинейного уравнения методом Ньютона для уравнения с одной переменной . Корень необходимо найти с точностью в качестве первого приближения .

Вариант решения нелинейного уравнения в программном комплексе MathCAD представлен на рисунке 3.

Результаты расчетов, а именно динамика изменения приближенного значения корня, а также погрешности расчета от шага итерации представлены в графической форме (см. рис.2).

Рис.2 . Результаты расчета по методу Ньютона для уравнения с одной переменной

Для обеспечения заданной точности при поиске приближенного значения корня уравнения в диапазоне необходимо выполнить 4 итерации. На последнем шаге итерации приближенное значение корня нелинейного уравнения будет определяться значением: .

Рис.3 . Листинг программы в MathCad

Модификации метода Ньютона для уравнения с одной переменной

Существует несколько модификаций метода Ньютона, которые направлены на упрощение вычислительного процесса.

Упрощенный метод Ньютона

В соответствии с методом Ньютона требуется вычислять производную функции f(x) на каждом шаге итерации, что ведет к увеличению вычислительных затрат. Для уменьшения затрат, связанных с вычислением производной на каждом шаге расчета, можно произвести замену производной f’( x_n ) в точке x_n в формуле на производную f’(x₀) в точке x₀. В соответствии с данным методом расчета приближенное значение корня определяется по следующей формуле:

Таким образом, на каждом шаге расчета строятся прямые , которые параллельны касательной к кривой y=f(x) в точке B₀ (см. рис.4). Преимуществом данного метода является то, что производная функции вычисляется один раз.

Разностный метод Ньютона

В соответствии с методом Ньютона требуется вычислять производную функции f(x) на каждом шаге итерации, что не всегда удобно, а иногда практически невозможно. Данный способ позволяет производную функции заменить разностным отношением (приближенным значением):

В результате приближенное значение корня функции f(x) будет определяться выражением разностного метода Ньютона:

Двух шаговый метод Ньютона

В соответствии с методом Ньютона требуется вычислять производную функции f(x) на каждом шаге итерации, что не всегда удобно, а иногда практически невозможно. Данный способ позволяет производную функции заменить разностным отношением (приближенным значением):

В результате приближенное значение корня функции f(x) будет определяться следующим выражением:

Метод секущих является двух шаговым, то есть новое приближение определяется двумя предыдущими итерациями и . В методе необходимо задавать два начальных приближения и . Скорость сходимости метода будет линейной.

Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.

Видео:4.2 Решение систем нелинейных уравнений. МетодыСкачать

Численные методы: решение нелинейных уравнений

Задачи решения уравнений постоянно возникают на практике, например, в экономике, развивая бизнес, вы хотите узнать, когда прибыль достигнет определенного значения, в медицине при исследовании действия лекарственных препаратов, важно знать, когда концентрация вещества достигнет заданного уровня и т.д.

В задачах оптимизации часто необходимо определять точки, в которых производная функции обращается в 0, что является необходимым условием локального экстремума.

В статистике при построении оценок методом наименьших квадратов или методом максимального правдоподобия также приходится решать нелинейные уравнения и системы уравнений.

Итак, возникает целый класс задач, связанных с нахождением решений нелинейных уравнений, например, уравнения или уравнения и т.д.

В простейшем случае у нас имеется функция , заданная на отрезке ( a , b ) и принимающая определенные значения.

Каждому значению x из этого отрезка мы можем сопоставить число , это и есть функциональная зависимость, ключевое понятие математики.

Нам нужно найти такое значение при котором такие называются корнями функции

Визуально нам нужно определить точку пересечения графика функции с осью абсцисс.

Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

Метод деления пополам

Простейшим методом нахождения корней уравнения является метод деления пополам или дихотомия.

Этот метод является интуитивно ясным и каждый действовал бы при решении задачи подобным образом.

Алгоритм состоит в следующем.

Предположим, мы нашли две точки и , такие что и имеют разные знаки, тогда между этими точками находится хотя бы один корень функции .

Поделим отрезок пополам и введем среднюю точку .

Тогда либо , либо .

Оставим ту половину отрезка, для которой значения на концах имеют разные знаки. Теперь этот отрезок снова делим пополам и оставляем ту его часть, на границах которой функция имеет разные знаки, и так далее, достижения требуемой точности.

Очевидно, постепенно мы сузим область, где находится корень функции, а, следовательно, с определенной степенью точности определим его.

Заметьте, описанный алгоритм применим для любой непрерывной функции.

К достоинствам метода деления пополам следует отнести его высокую надежность и простоту.

Недостатком метода является тот факт, что прежде чем начать его применение, необходимо найти две точки, значения функции в которых имеют разные знаки. Очевидно, что метод неприменим для корней четной кратности и также не может быть обобщен на случай комплексных корней и на системы уравнений.

Порядок сходимости метода линейный, на каждом шаге точность возрастает вдвое, чем больше сделано итераций, тем точнее определен корень.

Видео:15 Метод Ньютона (Метод касательных) Ручной счет Численные методы решения нелинейного уравненияСкачать

Метод Ньютона: теоретические основы

Классический метод Ньютона или касательных заключается в том, что если — некоторое приближение к корню уравнения , то следующее приближение определяется как корень касательной к функции , проведенной в точке .

Уравнение касательной к функции в точке имеет вид:

В уравнении касательной положим и .

Тогда алгоритм последовательных вычислений в методе Ньютона состоит в следующем:

Сходимость метода касательных квадратичная, порядок сходимости равен 2.

Таким образом, сходимость метода касательных Ньютона очень быстрая.

Запомните этот замечательный факт!

Без всяких изменений метод обобщается на комплексный случай.

Если корень является корнем второй кратности и выше, то порядок сходимости падает и становится линейным.

Упражнение 1. Найти с помощью метода касательных решение уравнения на отрезке (0, 2).

Упражнение 2. Найти с помощью метода касательных решение уравнения на отрезке (1, 3).

К недостаткам метода Ньютона следует отнести его локальность, поскольку он гарантированно сходится при произвольном стартовом приближении только, если везде выполнено условие , в противной ситуации сходимость есть лишь в некоторой окрестности корня.

Недостатком метода Ньютона является необходимость вычисления производных на каждом шаге.

Видео:Метод касательных (метод Ньютона)Скачать

Визуализация метода Ньютона

Метод Ньютона (метод касательных) применяется в том случае, если уравнение f(x) = 0 имеет корень , и выполняются условия:

1) функция y= f(x) определена и непрерывна при ;

2) f(a)·f(b) 0. Таким образом, выбирается точка с абсциссой x₀, в которой касательная к кривой y=f(x) на отрезке [a;b] пересекает ось Ox. За точку x₀ сначала удобно выбирать один из концов отрезка.

Рассмотрим метод Ньютона на конкретном примере.

Пусть нам дана возрастающая функция y = f(x) =x 2 -2, непрерывная на отрезке (0;2), и имеющая f ‘(x) = 2x > 0 и f »(x) = 2 > 0.

Уравнение касательной в общем виде имеет представление:

В нашем случае: y-y₀=2x₀·(x-x₀). В качестве точки x₀ выбираем точку B₁(b; f(b)) = (2,2). Проводим касательную к функции y = f(x) в точке B₁, и обозначаем точку пересечения касательной и оси Ox точкой x₁. Получаем уравнение первой касательной:y-2=2·2(x-2), y=4x-6.

Точка пересечения касательной и оси Ox: x₁ =

Рисунок 2. Результат первой итерации

Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x₁, получаем точку В₂ =(1.5; 0.25). Снова проводим касательную к функции y = f(x) в точке В₂, и обозначаем точку пересечения касательной и оси Ox точкой x₂.

Точка пересечения касательной и оси Ox: x₂ = .

Рисунок 3. Вторая итерация метода Ньютона

Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x₂, получаем точку В₃ и так далее.

В3 = ()

Рисунок 4. Третий шаг метода касательных

Первое приближение корня определяется по формуле:

= 1.5.

Второе приближение корня определяется по формуле:

=

Третье приближение корня определяется по формуле:

Таким образом, i-ое приближение корня определяется по формуле:

Вычисления ведутся до тех пор, пока не будет достигнуто совпадение десятичных знаков, которые необходимы в ответе, или заданной точности e — до выполнения неравенства |xi—xi-1|

using namespace std;

float f(double x) //возвращает значение функции f(x) = x^2-2

float df(float x) //возвращает значение производной

float d2f(float x) // значение второй производной

int _tmain(int argc, _TCHAR* argv[])

int exit = 0, i=0;//переменные для выхода и цикла

double x0,xn;// вычисляемые приближения для корня

double a, b, eps;// границы отрезка и необходимая точность

cin>>a>>b; // вводим границы отрезка, на котором будем искать корень

cin>>eps; // вводим нужную точность вычислений

if (a > b) // если пользователь перепутал границы отрезка, меняем их местами

if (f(a)*f(b)>0) // если знаки функции на краях отрезка одинаковые, то здесь нет корня

cout 0) x0 = a; // для выбора начальной точки проверяем f(x0)*d2f(x0)>0 ?

xn = x0-f(x0)/df(x0); // считаем первое приближение

cout eps) // пока не достигнем необходимой точности, будет продолжать вычислять

xn = x0-f(x0)/df(x0); // непосредственно формула Ньютона

> while (exit!=1); // пока пользователь не ввел exit = 1

Посмотрим, как это работает. Нажмем на зеленый треугольник в верхнем левом углу экрана, или же клавишу F5.

Если происходит ошибка компиляции «Ошибка error LNK1123: сбой при преобразовании в COFF: файл недопустим или поврежден», то это лечится либо установкой первого Service pack 1, либо в настройках проекта Свойства -> Компоновщик отключаем инкрементную компоновку.

Рис. 4. Решение ошибки компиляции проекта

Мы будем искать корни у функции f(x) = x2-2.

Сначала проверим работу приложения на «неправильных» входных данных. На отрезке [3; 5] нет корней, наша программа должна выдать сообщение об ошибке.

У нас появилось окно приложения:

Рис. 5. Ввод входных данных

Введем границы отрезка 3 и 5, и точность 0.05. Программа, как и надо, выдала сообщение об ошибке, что на данном отрезке корней нет.

Рис. 6. Ошибка «На этом отрезке корней нет!»

Выходить мы пока не собираемся, так что на сообщение «Exit?» вводим «0».

Теперь проверим работу приложения на корректных входных данных. Введем отрезок [0; 2] и точность 0.0001.

Рис. 7. Вычисление корня с необходимой точностью

Как мы видим, необходимая точность была достигнута уже на 4-ой итерации.

Чтобы выйти из приложения, введем «Exit?» => 1.

Видео:Вычислительная математика. Лекция 4. Решение нелинейных уравнений и систем уравненийСкачать

Метод секущих

Чтобы избежать вычисления производной, метод Ньютона можно упростить, заменив производную на приближенное значение, вычисленное по двум предыдущим точкам:

/

Итерационный процесс имеет вид:

где .

Это двухшаговый итерационный процесс, поскольку использует для нахождения последующего приближения два предыдущих.

Порядок сходимости метода секущих ниже, чем у метода касательных и равен в случае однократного корня .

Эта замечательная величина называется золотым сечением:

Убедимся в этом, считая для удобства, что .

Таким образом, с точностью до бесконечно малых более высокого порядка

Отбрасывая остаточный член, получаем рекуррентное соотношение, решение которого естественно искать в виде .

После подстановки имеем: и

Для сходимости необходимо, чтобы было положительным, поэтому .

Поскольку знание производной не требуется, то при том же объёме вычислений в методе секущих (несмотря на меньший порядок сходимости) можно добиться большей точности, чем в методе касательных.

Отметим, что вблизи корня приходится делить на малое число, и это приводит к потере точности (особенно в случае кратных корней), поэтому, выбрав относительно малое , выполняют вычисления до выполнения и продолжают их пока модуль разности соседних приближений убывает.

Как только начнется рост, вычисления прекращают и последнюю итерацию не используют.

Такая процедура определения момента окончания итераций называется приемом Гарвика.

Видео:10 Численные методы решения нелинейных уравненийСкачать

Метод парабол

Рассмотрим трехшаговый метод, в котором приближение определяется по трем предыдущим точкам , и .

Для этого заменим, аналогично методу секущих, функцию интерполяционной параболой проходящей через точки , и .

В форме Ньютона она имеет вид:

Точка определяется как тот из корней этого полинома, который ближе по модулю к точке .

Порядок сходимости метода парабол выше, чем у метода секущих, но ниже, чем у метода Ньютона.

Важным отличием от ранее рассмотренных методов, является то обстоятельство, что даже если вещественна при вещественных и стартовые приближения выбраны вещественными, метод парабол может привести к комплексному корню исходной задачи.

Этот метод очень удобен для поиска корней многочленов высокой степени.

Видео:МЗЭ 2021 Лекция 9 Метод Ньютона для решения нелинейных уравненийСкачать

Метод простых итераций

Задачу нахождения решений уравнений можно формулировать как задачу нахождения корней: , или как задачу нахождения неподвижной точки.

Пусть и — сжатие: (в частности, тот факт, что — сжатие, как легко видеть, означает, что).

По теореме Банаха существует и единственна неподвижная точка

Она может быть найдена как предел простой итерационной процедуры

где начальное приближение — произвольная точка промежутка .

Если функция дифференцируема, то удобным критерием сжатия является число . Действительно, по теореме Лагранжа

Таким образом, если производная меньше единицы, то является сжатием.

Условие существенно, ибо если, например, на [0,1] , то неподвижная точка отсутствует, хотя производная равна нулю. Скорость сходимости зависит от величины . Чем меньше , тем быстрее сходимость.

Рассмотрим уравнение: .

Если в качестве взять функцию , то соответствующая итерационная процедура будет иметь вид: . Как нетрудно убедиться, метод итераций в данном случае расходится при любой начальной точке , не совпадающей с собственно неподвижной точкой .

Однако можно в качестве можно взять, например, функцию . Соответствующая итерационная процедура имеет вид: .

Эти итерации сходятся к неподвижной точке для любого начального приближения :

Действительно, в первом случае , т.е. для выполнения условия необходимо чтобы , но тогда . Таким образом, отображение сжатием не является.

Рассмотрим , неподвижная точка та же самая, ситуация другая. Здесь, хотя формально производная может быть довольно большой (при малых ж), однако уже на следующем шаге она будет меньше 1.

т.е. такой итерационный процесс всегда сходится.

Метод Ньютона представляет собой частный случай метода простых итераций.

Здесь нетрудно убедиться, что при существует окрестность корня, в которой .

то если корень кратности , то в его окрестности и, следовательно,.

Если — простой корень, то сходимость метода касательных квадратичная (то есть порядок сходимости равен 2).

Поскольку , то

Таким образом, сходимость метода Ньютона очень быстрая.

Видео:9 класс, 11 урок, Методы решения систем уравненийСкачать

Нахождение всех корней уравнения

Недостатком почти всех итерационных методов нахождения корней является то, что они при однократном применении позволяют найти лишь один корень функции, к тому же, мы не знаем какой именно.

Чтобы найти другие корни, можно было бы брать новые стартовые точки и применять метод вновь, но нет гарантии, что при этом итерации сойдутся к новому корню, а не к уже найденному, если вообще сойдутся.

Для поиска других корней используется метод удаления корней.

Пусть — корень функции , рассмотрим функцию. Точка будет являться корнем функции на единицу меньшей кратности, чем, при этом все остальные корни у функций и совпадают с учетом кратности.

Применяя тот или иной метод нахождения корней к функции , мы найдем новый корень (который может в случае кратных корней и совпадать с ). Далее можно рассмотреть функцию и искать корни у неё.

Повторяя указанную процедуру, можно найти все корни с учетом кратности.

Заметим, что когда мы производим деление на тот или иной корень , то в действительности мы делим лишь на найденное приближение , и, тем самым, несколько сдвигаем корни вспомогательной функции относительно истинных корней функции . Это может привести к значительным погрешностям, если процедура отделения применялась уже достаточное число раз.

Чтобы избежать этого, с помощью вспомогательных функций вычисляются лишь первые итерации, а окончательные проводятся по исходной функции , используя в качестве стартового приближения, последнюю итерацию, полученную по вспомогательной функции.

Мы рассмотрели решение уравнений только в одномерном случае, нахождение решений многомерных уравнений существенно более трудная задача.

📹 Видео

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

Метод Ньютона для решения нелинйеных уравнений в MS ExcelСкачать

Метод Ньютона | Лучший момент из фильма Двадцать одно 21Скачать