Публикую первую часть второй главы лекций по теории автоматического управления.
В данной статье рассматриваются:
2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
2.2. Линеаризация уравнений динамики САУ (САР)
2.3. Классический способ решения уравнений динамики
Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.
Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.
- 2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
- 2.2. Линеаризация уравнений динамики САУ (САР)
- Пример
- 2.3. Классический способ решения уравнений динамики
- Пример
- Математическое описание линейных систем автоматического управления.
- В чем состоит задача линеаризации уравнений сау
- 📹 Видео
Видео:Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 3.5. Линеаризация систем диф.уровСкачать

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
При составлении уравнений, описывающих нестационарные процессы в САУ (САР) и которые в дальнейшем будем называть уравнениями динамики, система “разбивается” на отдельные элементы (звенья), для каждого из которых не существует проблем в записи соответствующего уравнения динамики.
На рис. 2.1.1 представлено схематичное представление САУ (звена) в переменных «вход-выход», где x(t) (или u(t)) — входное воздействие, а y(t) — выходное воздействие, соответственно. Нередко входное воздействие будет называться управляющим, а выходное воздействие — регулируемой величиной (переменной).
При составлении уравнений динамики используются фундаментальные законы сохранения из разделов “Механики”, “Физики”, “Химии” и др.
Например, при описании перемещения узла какого-то механизма силового привода используются законы сохранения: момента, энергии, импульса и др… В теплофизических (теплогидравлических) системах используются фундаментальные законы сохранения: массы (уравнение неразрывности), импульса (уравнение движения), энергии (уравнение энергии) и др
Уравнения сохранения в общем случае содержат постоянные и нестационарные члены, причем при отбрасывании нестационарных членов получают так называемые уравнения статики, которые соответствуют уравнениям равновесного состояния САУ (звена). Вычитанием из полных уравнений сохранения стационарных уравнений получают нестационарные уравнения САУ в отклонениях (от стационара).
где: — стационарные значения входного и выходного воздействий;
— отклонения от станционара, соотвесвенно.
В качестве примера рассмотрим «технологию» получения уравнений динамики для механического демпфера, схематическое изображение которого представлено на рис. 2.1.2.
Согласно 2-му закону Ньютона, ускорение тела пропорционально сумме сил, действующих на тело:
где, m — масса тела, Fj — все силы воздействующие на тело (поршень демпфера)
Подставляя в уравнение (2.1.1) все силы согласно рис. 2.2, имеем:
где — сила тяжести;
— сила сопротивления пружины,
— сила вязконо трения (пропорциональна скорости поршеня)
Размерности сил и коэффициентов, входящих в уравнение (2.1.2):
Предполагая, что при t ≤ 0 поршень демпфера находился в равновесии, то есть
перейдем к отклонениям от стационарного состояния:
Пусть при t>0 . Тогда, подставляя эти соотношения в уравнение (2.1.2), получаем:
если , то уравнение принимает вид:
Соотношение (2.1.4) – уравнение звена (демпфера) в равновесном (стационарном) состоянии, а соотношение (2.1.5) – статическая характеристика звена – демпфера (см. рисунок 2.1.3).
Вычитая из уравнения (2.1.3) уравнение (2.1.4), получаем уравнение динамики демпфера в отклонениях:
тогда, разделив на k, имеем:
Уравнение (2.1.6) — это уравнение динамики в канонической форме, т.е. коэффициент при Δy(t) равен 1.0!
«Легко» видеть, что коэффициенты перед членами, содержащими производные, имеют смысл (и размерность!) постоянных времени. В самом деле:
Таким образом, получаем, что:
— коэффициент перед первой производной имеет размерность [c] т.е. смысл некоторой постоянной времени;
— коэффициент перед второй производной: [];
— коэффициент в правой части (): [
].
Тогда уравнение (2.1.6) можно записать в операторной форме:
, что эквивалентно
где: — оператор диффренцирования;
-линейный дифференциальный оператор;
— линейный дифференциальный оператор, вырожденный в константу, равную
.
Анализ уравнения (2.1.6.а) показывает, что такое уравнение имеет размерные переменные, а также размерными являются все коэффициенты уравнения. Это не всегда удобно. Кроме того, если реальная САР (САУ) состоит из многих звеньев, выходными воздействиями которых являются различные физические переменные (скорость, температура, нейтронный поток, тепловой поток и т.д.), то значения коэффициентов могут различаться на большое число порядков, что ставит серьезные математические проблемы при численном решении уравнений динамики на компьютере (поскольку числа в компьютере всегда представляются с какой-то точностью). Одним из наилучших способов избежать численных трудностей является принцип нормализации, т.е. переход к безразмерным отклонениям, которые получены нормированием отклонения на стационарное значение соответствующей переменной.
Введем новые нормированные (безразмерные) переменные:
Подставляя эти соотношения в уравнение (2.1.2), имеем:
Поддчеркнутые члены выражения в сумме дают 0 (см. 2.1.4) Перенося в левую часть члены, содержащие , и, разделив на
, получаем:
где: — коэффициент усиления, причем безразмерный.
Проверим размерность коэффициента
Использованный выше «технический» прием позволяет перейти к безразмерным переменным, а также привести вид коэффициентов в уравнении динамики к легко интерпретируемому виду, т.е. к постоянным времени (в соответствующей степени) или к безразмерным коэффициентам усиления.
На рис. 2.1.4 представлены статические характеристики для механического демпфера:
Процедура нормировки отклонений позволяет привести уравнения динамики к виду:
где дифференциальные операторы.
Если дифференциальные операторы — линейные, а статическая характеристика САУ (звена) – тоже линейна, то выражение (2.1.8) соответствует линейному обыкновенному дифференциальному уравнению (ОДУ).
А если – нелинейные дифференциальные операторы, или
, то уравнение динамики — нелинейное. Под нелинейными действиями понимаются все математические действия, кроме сложения (+) и вычитания (-).
Пример создания модели демпфера можно посмотереть здесь: «Технология получения уравнений динамики ТАУ»
Видео:Теория автоматического управления. Лекция 5. Гармоническая линеаризацияСкачать

2.2. Линеаризация уравнений динамики САУ (САР)
Практически все реальные системы автоматического управления (САУ) являются нелинейными, причем нелинейность САУ может определяться различными причинами:
- Нелинейностью статической характеристики.
- Нелинейностью динамических членов в уравнениях динамики.
- Наличием в САУ принципиально нелинейных звеньев.
Если в замкнутой САУ (САР) нет принципиально нелинейных звеньев, то в большинстве случаев уравнения динамики звеньев, входящих в систему, могут быть линеаризованы. Линеаризация основана на том, что в процессе регулирования (т.е. САУ с обратной связью) все регулируемые величины мало отклоняются от их программных значений (иначе система регулирования или управления не выполняла бы своей задачи).
Например, если рассмотреть управление мощностью энергетического ядерного реактора, то главная задача САР — поддержание мощности на заданном (номинальном) уровне мощности. Существующие возмущения (внутренние и внешние) “отрабатываются” САР и поэтому параметры ядерного реактора незначительно отличаются от стационарных. На рис. 2.2.1 представлена временная зависимость мощности ядерного реактора, где нормированные отклонения мощности ΔN /N0 Рис. 2.2.1 – Пример изменения мощности реактора
Рассмотрим некоторое звено (или САР в целом), описание динамики которого можно представить в переменных “вход-выход”:
Предположим, что динамика данного звена описывается обыкновенным дифференциальным уравнением n-го порядка:
Перенесем в левую часть уравнения и запишем уравнение в виде%
где -– функция регулируемой переменной и ее производных, а также управляющего (входного) воздействия и его производных, причем F – обычно нелинейная функция.
Будем считать, что при t ≤ 0 САУ (звено) находилось в равновесии (в стационарном состоянии). Тогда уравнение (2.2.2) вырождается в уравнение статической характеристики:
Разложим левую часть уравнения (2.2.2) в ряд Тейлора в малой окрестности точки равновесного состояния .
Напомним, что разложение в ряд Тейлора трактуется следующим образом: если , то «простое» разложение функции в ряд Тейлора в окрестности точки
будет выглядеть так:
C учетом вышеприведенного разложение принимает вид:
Предполагая, что отклонения выходных и входных воздействий незначительны, (т.е.:), оставим в разложении только члены первого порядка малости (линейные). Поскольку
, получаем:
Подставляя соотношение (2.2.4) в уравнение (2.2.2), и перенося множители при у и u в разные части получаем уравнения:
Коэффициенты — постоянные коэффициенты, поэтому уравнения 2.2.5 — линейное дифференциальное с постоянными коэффициентами.
В дальнейшем нами будет часто использоваться операторная форма записи уравнений динамики:
где – оператор дифференцирования;
— линейный дифференциальный оператор степени n;
— линейный дифференциальный оператор степени m, причем обычно порядок оператора
выше порядка оператора
:
Уравнения (2.2.5) и (2.2.6) — уравнения динамики системы (звена) в отклонениях.
Если исходное уравнение (2.2.1) — дифференциальное уравнение в физических переменных (температура, скорость, поток и т.д.), то размерность коэффициентов может быть произвольной (любой).
Переход к нормализованным отклонениям позволяет “упорядочить” размерность коэффициентов. В самом деле, разделив уравнение (2.2.5) на начальные условия (значения в нулевой момент времени) и выполнив некоторые преобразования, получаем:
Приведение уравнения динамики САУ (звена) к нормализованному виду позволяет “унифицировать” размерность коэффициентов уравнений: ==>
Если вынести в правой части (2.2.7) коэффициент за общую скобку и разделить все уравнение на
, то уравнение принимает вид:
или в операторном виде:
Линеаризация уравнений динамики и нормализация переменных позволяют привести уравнения динамики САУ (звена) к виду, наиболее удобному для использования классических методов анализа, т.е. к нулевым начальным условиям.
Пример
Выполнить линеаризацию уравнения динамики некоторой «абстрактной» САР в окрестности состояния (x0, y0), если полное уравнение динамики имеет вид:
Нелинейность полного уравнения динамики проявляется в следующем:
• во-первых, в нелинейности статической характеристики:
• во-вторых, слагаемое в левой части — чисто нелинейное, так как действие умножения является нелинейным.
Выполним процесс линеаризации исходного уравнения, динамики без разложения я ряд Тейлора, основываясь на том, что в окрестности состояния (x0, y0) нормированные отклонения управляющего воздействия и регулируемой величины намного меньше 1.
Преобразования выполним в следующей последовательности:
- Перейдем к безразмерным переменным (нормализованным);
- Выполним линеаризацию, отбросив нелинейные члены 2-го и выше порядков малости.
Перейдем к новым безразмерным переменным:
Заметим, что: .
Подставляя значения x(t) и y(t) в исходное уравнение:
Удаляем полученного уравнения уравнения стационара: , а так же пренебрегая слагаемыми второго прядка малости:
, получаем следующее уравнение:
Вводим новые обозначения:
Получаем уравнения в «почти» классическом виде:
Если в правой части вынести за общую скобку и разделить все уравнение на
, то уравнение (линеаризованное) принимает вид:
Процедура нормализации позволяет более просто линеаризовать уравнение динамики, так как не требуется выполнять разложение в ряд Тейлора (хотя это и не сложно).
Видео:Теория автоматического регулирования. Лекция 2. Линеаризация характеристик звеньев САУСкачать

2.3. Классический способ решения уравнений динамики
Классический метод решения уравнений динамики САУ (САР) применим только для линейных или линеаризованных систем.
Рассмотрим некоторую САУ (звено), динамика которой описывается линейным дифференциальным уравнением вида:
Переходя к полной символике, имеем:
Выражение (2.3.2) — обыкновенное дифференциальное уравнение (ОДУ), точнее неоднородное ОДУ, так как правая часть ≠ 0.
Известно входное воздействие x(t), коэффициенты уравнения и начальные условия (т.е. значения переменных и производных при t = 0).
Требуется найти y(t) при известных начальных условиях.
где: — решение однородного дифференциального уравнения
y_(t) $inline$ — частное решение. $inline$
Будем называть решение однородного дифференциального уравнения , собственным решением, так как его решение не зависит от входного воздействия, а полностью определяется собственными динамическими свойствами САУ (звена).
Вторую составляющую решения (2.3.3) будем называть , вынужденным, так как эта часть решения определяется внешним воздействием
, поэтому САУ (САР или звено) “вынуждена отрабатывать” это воздействие:
Напомним этапы решения:
1) Если имеется уравнение вида , то сначала решаем однородное дифференциальное уравнение:
2) Записываем характеристическое уравнение:
3) Решая уравнение (2.3.5), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения
4) Тогда собственное решение записывается в виде:
если среди нет повторяющихся корней (кратность корней равна 1).
Если уравнение (2.3.5) имеет два совпадающих корня, то собственное решение имеет вид:
Если уравнение (2.3.5) имеет k совпадающих корней (кратность корней равна k), то собственное решение имеет вид:
5) Вынужденную часть решения можно найти различными способами, но наиболее распространены следующие способы:
а) По виду правой части.
б) Методом вариации постоянных.
в) Другие методы…
Если вид правой части дифференциального уравнения – относительно несложная функция времени, то предпочтительным является способ а): подбор решения. .
6) Суммируя полученные составляющие (собственную и вынужденную), имеем:
7) Используя начальные условия (t = 0), находим значения постоянных интегрирования .
Обычно получается система алгебраических уравнений.
Решая систему, находим значения постоянных интегрирования
Пример
Найти аналитическое выражение переходного процесса на выходе звена, если
Решение. Запишем однородное ОДУ:
Характеристическое уравнение имеет вид: ; Решая, имеем:
тогда:
где — неизвестные (пока) постоянные интегрирования.
По виду временной функции в правой части запишем как:
Подставляя в исходное уравнение, имеем:
Суммируя , имеем:
Используя 1-е начальное условие (при t = 0), получаем: , а из 2-го начального условия имеем:
Решая систему уравнений относительно и
, имеем:
Тогда окончательно:
Что бы проверить результ, выполним моделирование процесса в SimInTech, для этого преобразуем исходное уравнение к виду:
Создадим модель SimInTech, содержащую исходное динамическое уравнение и полученное аналитическое решение, и выведем результаты на один график (см. рис. 2.3.1).

Рис. 2.3.1 – структурная схема для проверки решения
На рис. 2.3.2 приведено решение по вышеприведенному соотношению и численное решение задачи в среде SimInTech (решения совпадают и линии графиков «наложены» друг на друга).
Видео:7) ТАУ для чайников.Части 3.4 и 3.5 : Передаточная функция. Преобразование Лапласа...Скачать

Математическое описание линейных систем автоматического управления.
ЛЕКЦИЯ 2.
3.Математическое описание линейных САУ. Линеаризация.
Математическое описание линейных систем автоматического управления.
Порядок исследования САУ включает математическое описание системы, исследование ее установившихся режимов и исследование переходных режимов.
Математическое описание системы, т.е. получение ее математической модели, начинается с разбиения ее на звенья и описания этих звеньев. Это описание может осуществляться либо аналитически в виде уравнений, связывающих входные и выходные величины звена, либо графически в виде характеристик, описывающих ту же связь. По уравнениям или характеристикам отдельных звеньев составляются уравнения или характеристики системы в целом, на основании которых и исследуется система.
На прошлой лекции было дано понятие о функциональной схеме САУ (Рис. 2).
В функциональной схеме система разбита на звенья исходя из выполняемых ими функций, т.е. назначения. Для математического описания систему разбивают на звенья по другому принципу, а именно – исходя из удобства получения этого описания. Для этого систему следует разбивать на возможно более простые («мелкие») звенья, но вместе с тем необходимо, чтобы они обладали направленностью действия.
Звеном направленного действия называется звено, передающее воздействие только в одном направлении – с входа на выход, так что изменение состояния такого звена не влияет на состояние предшествующего звена, работающего на его вход. В результате при разбиении системы на звенья направленного действия математическое описание каждого такого звена может быть составлено без учета связей его с другими звеньями. Соответственно, математическое описание всей системы в целом может быть получено как совокупность составленных независимо друг от друга уравнений или характеристик отдельных звеньев, образующих систему, дополненных уравнениями связи между звеньями.
В результате разбиения САУ на звенья направленного действия и получения математического описания звеньев составляется структурная схема системы, которая и является ее математической моделью. Структурная схема системы состоит из прямоугольников, изображающих звенья схемы, и стрелок, соединяющих выходы и входы звеньев согласно связям между звеньями в системе. Стрелками показываются также внешние воздействия, приложенные к отдельным звеньям системы. Каждому звену структурной схемы придается описывающее его уравнение или характеристика. При этом уравнение обычно записывается прямо на схеме внутри изображающего звено прямоугольника в виде передаточной функции. Получение структурной схемы является конечной целью математического описания системы.
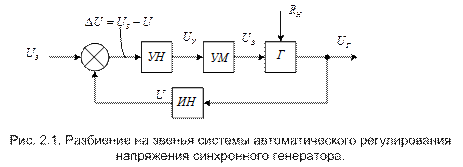
В качестве примера на рис. 2.1 показано разбиение на звенья системы автоматического регулирования напряжения синхронного генератора, которая была дана на прошлой лекции (Рис. 5), т.е. замкнутая система управления по отклонению. При этом принято, что усилитель регулятора состоит из двух частей: усилителя напряжения УН и усилителя мощности УМ в виде, например, электромашинного усилителя. Каждый из этих усилителей обладает направленностью действия и поэтому может быть выделен в виде отдельного звена.
На рис.2.1 стрелками показаны внешние воздействия – задающее воздействие 
Основная сложность, которая существует при выводе уравнений звеньев системы, заключается в необходимости установления допустимой степени идеализации и упрощения звеньев. Главным упрощением, к которому следует стремиться при выводе уравнений звеньев системы, является их линеаризация, т.е. описание линейными дифференциальными уравнениями. Линеаризация нелинейности, содержащейся в уравнении звена, заключается в замене этой нелинейности приближенной линейной зависимостью.
Мы не будем подробно останавливаться на математическом аспекте процедуры линеаризации. В двух словах можно сказать, что процедура линеаризации заключается в замене нелинейного дифференциального уравнения приближенным линейным. Понятно, что такую замену невозможно с достаточной степенью точности осуществить во всей области определения входных и выходных величин. Поэтому область линеаризации ограничивают вблизи некоторого номинального режима. Выбор такого номинального режима является, в общем случае, нетривиальной задачей. На практике чаще всего в качестве такого номинального режима выбирают установившийся режим, т.е. режим функционирования системы при времени, стремящемся к бесконечности (t®¥). Установивщийся режим, как мы знаем, характеризуется установившимися значениями выходной и входной величин – y0 и x0, соответсвенно.
Рис. 2.2. Геометрическая интерпретация линеаризации.
Дадим геометрическую интерпретацию линеаризации. Изобразим графически нелинейную зависимость. Текущие значения координат y и x запишем как:
| y(t) = y0 + Dy(t); x(t) = x0 + Dx(t). | , где x(t), y(t) | – текущие значения, |
| y0, x0 | – установившиеся значения, | |
| Dy(t), Dx(t) | – отклонения от установившихся значений. |
В точке (x0, y0), определяемой установившимися значениями, заменим участок кривой касательной и получим прямую, описываемую линейным уравнением:
| y = yн + kx | , где yн | – постоянная величина; |
| k = [dy(t)/dx(t)]0 | – коэффициент, определяемый наклоном касательной к кривой в точке (x0, y0). |
Для исключения из уравнения величины yн перенесем начало координат в точку (x0, y0). Тогда получим линейное уравнение, связывающее между собой отклонения переменных величин от своих установившихся значений, вида:
Таким образом, линеаризация уравнения геометрически может трактоваться как замена первоначальной кривой на касательную к ней прямую в точке установившегося режима. Очевидно, что эта замена тем точнее, чем меньше величины отклонений координат элемента от своих установившихся значений в исследуемом динамическом процессе.
Рассмотрим звено, описываемое нелинейной статической зависимостью Y=φ(X).
Пусть установившийся режим звена соответствует значениям входной и выходной величин X0 и Y0 (рис.2.2) и отклонения Х от Х0 в процессе работы звена достаточно малы. В этом случае исходную нелинейную зависимость Y=φ(X) можно разложить в ряд Тейлора в окрестностях точки установившегося режима и, отбросив члены ряда выше первого порядка малости, получить следующую приближенную зависимость:
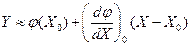
где 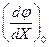
Это уравнение можно переписать в таком окончательном виде:
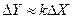

Таким образом, линеаризация уравнения геометрически может трактоваться как замена первоначальной кривой на касательную к ней прямую в точке установившегося режима. Очевидно, что эта замена тем точнее, чем меньше величины отклонений координат элемента от своих установившихся значений в исследуемом динамическом процессе.
Коэффициент k в уравнении равен тангенсу угла наклона этой касательной относительно оси абсцисс. Поэтому его величина может быть найдена чисто графическим построением без нахождения аналитического выражения для исходной нелинейной зависимости φ(Х), как было показано ранее.
Рассмотрим теперь более общий случай, когда звено описывается нелинейным уравнением, включающим производные по времени от входной и выходной величин:
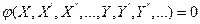
Такое уравнение называется динамическим. Оно характеризует переходный процесс, который протекает в системе.
Разложив, как и прежде, нелинейную функцию, находящуюся в левой части уравнения, в ряд Тейлора в точке установившегося режима, получим следующее линейное дифференциальное уравнение для приращений переменных:
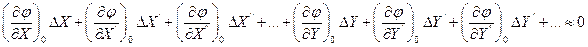
Здесь 
Показанная процедура линеаризации нелинейных звеньев приводит к приближенному описанию их линейными дифференциальными уравнениями в отклонениях.
В ТАУ приняты определенные формы записи линеаризованных дифференциальных уравнений звеньев. При этом уравнение (2.1) (с учетом только приведенных там членов) должно записываться так:

Здесь 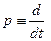
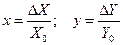


Особенности приведенной формы записи заключаются в следующем. Выходная величина и ее производные находятся в левой части уравнения, а входная величина и ее производные – в правой. Коэффициент при приращении выходной величины равен единице [в результате деления обеих частей уравнения на 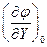
Коэффициенты левой части уравнения – постоянные времени. Размерность их – секунда в степени, равной порядку производной, перед которой стоит данный коэффициент.
Другой формой записи линейных уравнений звеньев является запись с помощью передаточной функции. Уравнение (2.2) при этом принимает вид:
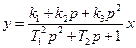
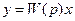

Дробь W(p) называется передаточной функцией звена. Пока будем рассматривать ее просто как удобный способ записи дифференциальных уравнений. Полное определение передаточной функции дам дальше, когда будем рассматривать преобразование Лапласа.
Рассматривая выше формы записи уравнений, принятые в ТАУ, мы оперировали для определенности уравнением 2-го порядка с одной входной величиной х. Однако в результате линеаризации реальных звеньев могут быть получены уравнения любого порядка. В общем случае звено САУ, имеющее n входов, описывается дифференциальным уравнением

или в другом виде
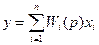
Здесь xi – входные воздействия на звено (i = 1,2,…,n); Q(p) и Ri(p) – полиномы относительно р; 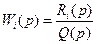
5.Применение преобразования Лапласа для решения линейных дифференциальных уравнений.
Видео:Составление и линеаризация дифференциального уравнения центробежного маятникаСкачать

В чем состоит задача линеаризации уравнений сау
Название работы: Методы линеаризации нелинейных САУ
Предметная область: Математика и математический анализ
Описание: Методы линеаризации нелинейных САУ. НСдинамика кх описывается нелинми диф урми это сисмы имеющие нелинейную стстю харку. Нелинейность обусловлена нелинейностью статической характеристики одного из элементов системы. Методы линеаризации нелинейных САУ.
Дата добавления: 2013-11-15
Размер файла: 1.05 MB
Работу скачали: 77 чел.
25. Методы линеаризации нелинейных САУ.
С т. зрения передачи и преобразования сигнала НЛ отлич. от линейных систем тем, что мгновенный коэфффициент передачи зависит от значения входного сигнала. САУ, содержащие звенья, динамика которых описывается НЛ дифференц. уравнениями относят к НЛ системам .
НС-динамика к-х описывается нелин-ми диф ур-ми, это сис-мы, имеющие нелинейную стст-ю хар-ку.
Систему можно представить в виде соединения из 2-х элементов:
ЛЧ описывается обычными диф ур-ми с пост-ми коэфф-ми.
НЭ является безинерционным и его выходная величина и вход. величина связаны связаны между собой НЛ алгебраическим уравнением. Нелинейность обусловлена нелинейностью статической характеристики одного из элементов системы.
Методы линеаризации нелинейных САУ.
метод гармонической линеаризации
совместная стат и гармон линеаризация
Метод гармонической линеаризации.
Сущность метода гарм-ой линеаризации заключается в отыскании периодического решения на входе нелинейного элемента, разложение сигнала на выходе нелинейного элемента в ряд Фурье и замены вых сигнала его первой гармоникой. Такая замена справедлива если сис или ЛЧ явл-ся фильтром низкой частоты, т.е. подавляет высшие гармоники.
В рез-те линеаризации нелин стат хар-ку заменяют эквивалентным линейным звеном с коэффициентами
И для гистерезисных хар-ик (петлевых) значение k / Г всегда получается отрицательным, т.е. в ур-ие вводят производную с отриц знаком и эта производная дает запаздывание в работе звена. Такую линеар-ю наз-т гармонической т.к. она связана с разложением нелин колебаний на гармонич-ие составляющие.
k / Г и k Г гарм-ие коэф-ты усиления нелин звена.
Отличия гарм-ой линеар-ии от обычной:
При гарм-ой линеаризации нелин хар-ку заменят прямой, крутизна которой зависит от амплитуды входного сигнала.
Гарм-ая линеаризация позволяет вместо нелин звена получить линейное, к-т усиления которого зависит от а.
Гарм-ая линеар-ия дает возможность опредилить св-ва нелин САУ методами линейной теории автом-х сис-м.
Этот метод приближенного исследования точности нелин сис в стационарных случ реж-ах.
В качестве примера возьмем нелин звено со стат хар-ой типа насыщение.
Пусть на входе стационарный случ. Сигнал.
X ( t )= m x + x 0 ( t )
Задача стат лин-ии закл-ся в том чтобы найти линейное звено дающее при том же вх сигнале x ( t ) вых сигнал = эквивалентному вых сигналу нелин звена при этом надо чтобы эквив-й сигнал максимально приближался к y ( t ).
Точность линеариз зависит от того, какой критерий выбран для сравнения y экв и y .
Сущ 2 критерия сравнения y экв и y :
1. по первому способу линеаризация осущ-ся исходя из след условий
при выполнении первого условия линейное звено будет полностью эквивалентно исх-му нелин звену в отношении пропускания заданной детерменированной составляющей вх сигнала. Второе условие означает эквивалентность в отношении пропускания центрированной случ составляющей вх сигнала. В связи с тем что дисперсия не определяет полностью закона распределения случ величины выбор ур-ия эквивалентного линейного звена только по дисперсии определяет погрешность данной стат линеаризации.
2. основан на линеаризации разности
К-ты стат линеар-ии:
Совместная статическая и гармоническая линеаризация.
Случай когда в сис присутствуют автоколебания и на вх сис подаются случ воздействия:
x(t)=m x +x 0 (t)+a*sin w a t
Из-за неприменимости принципа суперпозиции необходимо учитывать наличие всех 3-х составляющих для этого надо осущ-ть совместную стат и гарм линеа-ию, в рез-те этого сигнал на выходе:
в случ симметр-ой нелин стат хар-ки пост состав-ую
m y = y 0 = k сг0 m x
эти 4 к-та опред-ся по фор-ам для гарм-ой и стат линеар-ии. Эти к-ты уже будут зависеть от 4-х составляющих ( m x , s x , a , w a )
При исследовании сис m x , s x , a , w a — определяются совместным решением ур-ий для колебательной составляющей и для случ состав-ей.
Применяя совместно стат и гармонич линеаризацию можно решать две задачи:
можно исследовать влияние внешних случ воздействий на параметры возможных автоколебаний.
можно исследовать точность сис в случ режимах при наличии сис гармонических колебаний.
Испол-ся для исключения эффекта наличия нелин-х хар-к (люфт и зона нечувст-ти).
При виб-ой лин-ии на вх нелин звена на постоянный или медленно изменяющиюся сигнал накладывается высокочастотная состав-ая и в рез-те этого нелин звено пропускает пост сост-ую как пропорциональное звено.
Рассмотрим метод виб-ой лин-ии на примере релейной сис:
зависимость y 0 = f ( x 0 ) ,где y 0 зависит от x 0 и от формы нелин-ой стат хар-ки, т.о. при наличии переменного воздействия , этот элемент пропускает пост воздействие x 0 как звено непрерывного действия.
Сам процесс виб-й лин-ии можно трактовать как процесс модуляции, в данном примере реле явл-ся модулятором высокочас-ое воздействие — сигнал несущей частоты, а НЧ вх сигнал x 0 явл-ся модулирующим сигналом. В данном случае осущ-ся ШИМ и ф-ей модулир-го сигнала явл-ся ширина вых имп-са и условие неискаженной передачи НЧ-составляющей явл-ся f ВЧ / f НЧ >=3
Когда реле работает в составе САУ обычно НЧ сигнал x 0 представляет собой сигнал управления и изменения во времени x 0 и есть перех-ой процесс в сис.
ВЧ воздействие осущ виб-ой лин-ей м.б. получено 3-я способами:
С пом внешнего генератора, создающего вынужд-е колебания на вх нелин элемента.
📹 Видео
Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

3) ТАУ для чайников. Часть 2.2: Математические модели...Скачать

Метод пространства состояний САУ: описание конкретной системыСкачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Алгоритмы. Линеаризация функцийСкачать

Теория автоматического управления. Лекция 6. Структурные схемы САУСкачать
2) ТАУ для чайников. Часть 2.1: Математические модели...Скачать

Теория автоматического управления. Лекция 6. Гармонический балансСкачать

Raport 2 0 Линеаризация или Ввод индивидуальных пользовательских характеристик в интеллектуальныеСкачать

АУПО. Математическая модель продольного движения. ЛинеаризацияСкачать

Теория автоматического управления. Лекция 7. Дискретные САУ. Алгебраический критерий устойчивостиСкачать

Линейные системы автоматического регулирования. Лекция 1. Классификация САУСкачать

№11. Понятие устойчивости. Общая постановка задачи устойчивости по А.М.Ляпунову.Скачать