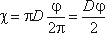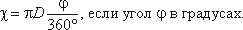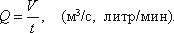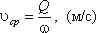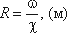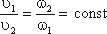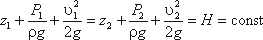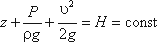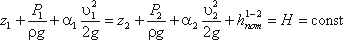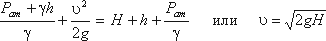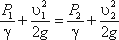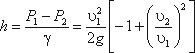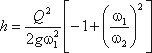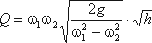В чем отличие уравнения бернулли для потоков идеальной и реальной жидкостей (8 видео)

В чем отличие уравнения бернулли для потоков идеальной и реальной жидкостей

Гидродинамика — раздел гидравлики, в котором изучаются законы движения жидкости и ее взаимодействие с неподвижными и подвижными поверхностями.

Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.

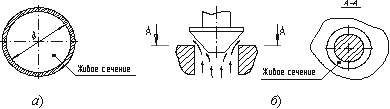
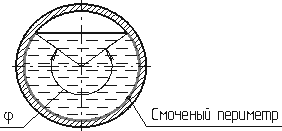
Живым сечением ω (м²) называют площадь поперечного сечения потока, перпендикулярную к направлению течения. Например, живое сечение трубы — круг (рис.3.1, б); живое сечение клапана — кольцо с изменяющимся внутренним диаметром (рис.3.1, б).

Смоченный периметр χ («хи») — часть периметра живого сечения, ограниченное твердыми стенками (рис.3.2, выделен утолщенной линией).

Для круглой трубы

если угол в радианах, или

Расход потока Q — объем жидкости V, протекающей за единицу времени t через живое сечение ω.

Средняя скорость потока υ — скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω

Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.

Гидравлический радиус потока R — отношение живого сечения к смоченному периметру

Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени

Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным

Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.

Трубка тока — трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока называется элементарной струйкой.

Течение жидкости может быть напорным и безнапорным. Напорное течение наблюдается в закрытых руслах без свободной поверхности. Напорное течение наблюдается в трубопроводах с повышенным (пониженным давлением). Безнапорное — течение со свободной поверхностью, которое наблюдается в открытых руслах (реки, открытые каналы, лотки и т.п.). В данном курсе будет рассматриваться только напорное течение.

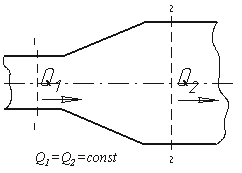
Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений. Представим трубу с переменным живым сечением (рис.3.4). Расход жидкости через трубу в любом ее сечении постоянен, т.е. Q₁=Q₂= const, откуда

Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:

Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг задач.

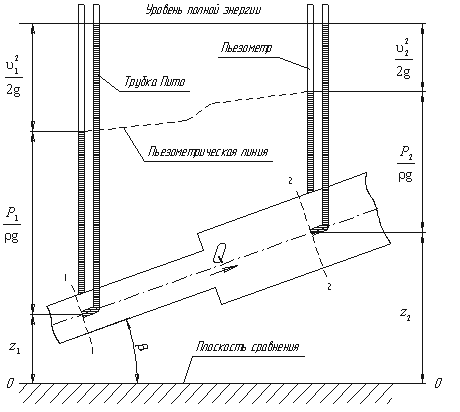
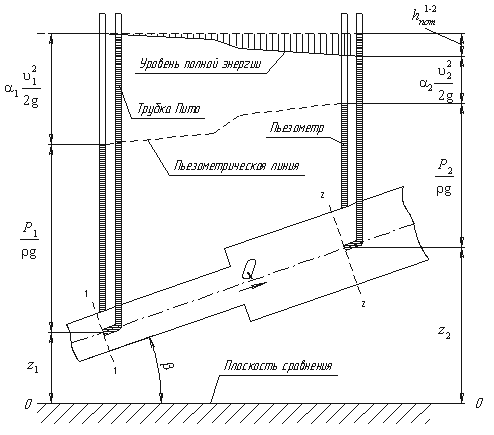
Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.3.5).

Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.

Для измерения давления жидкости применяют пьезометры — тонкостенные стеклянные трубки, в которых жидкость поднимается на высоту 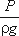. В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.

Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.

Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.3.5).

Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.

Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.

Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:

Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:

и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.

С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:

z1 и z2 — удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2;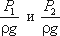
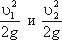
— удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;
— удельные кинетические энергии в тех же сечениях.

Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.

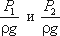
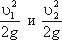
Уравнение Бернулли можно истолковать и чисто геометрически. Дело в том, что каждый член уравнения имеет линейную размерность. Глядя на рис.3.5, можно заметить, что z1 и z2 — геометрические высоты сечений 1-1 и 2-2 над плоскостью сравнения; — пьезометрические высоты; — скоростные высоты в указанных сечениях.

В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.

Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения

Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).

Потерянная энергия или потерянный напор обозначаются и имеют также линейную размерность.

Уравнение Бернулли для реальной жидкости будет иметь вид:

Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.

Кроме этого в уравнении появились еще два коэффициента α₁ и α₂, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ).

Потерянная высота складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)

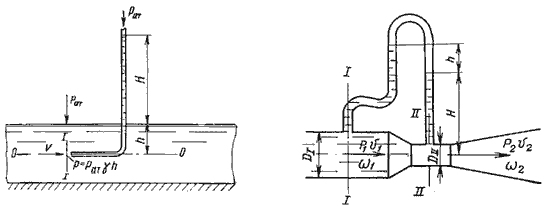
Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.3.7), загнутый конец которой направлен навстречу потоку. Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим

где Н — столб жидкости в трубке Пито.

Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.

Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и II-II:

Выражение, стоящее перед 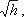, является постоянной величиной, носящей название постоянной водомера Вентури.

Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.

Содержание

Уравнение Бернулли
Смысл уравнения Бернулли
Уравнение Бернулли для элементарной струйки реальной жидкости
Уравнение Бернулли для потока реальной жидкости
Уравнение Бернулли для элементарной струйки и потока реальной жидкости
Дифференциальные уравнения Эйлера движения невязкой жидкости
Уравнение движения Навье-Стокса
🔍 Видео

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Уравнение Бернулли

Уравнение Бернулли для струйки жидкости формулируется следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

Уравнение Бернулли выглядит так:

Подробное описание всех входящих в состав уравнения параметров уже описан в этой статье.

Содержание статьи

Видео:Закон БернуллиСкачать

Смысл уравнения Бернулли

По существу вывода уравнение Бернулли для струйки идеальной жидкости представляет собой закон сохранения механической энергии, составленный применительно к единице массового расхода жидкости. Это следует из того, что в процессе вывода значения работы сил, приложенных к выделенному объему струйки и значения кинетической энергии этого объема были поделены на величину ρqΔT.

Отсюда вытекает, что поскольку член υ 2 /2 является мерой кинетической энергии единицы массы движущейся жидкости, то сумма членов gz+p/ρ будет мерилом ее потенциальной энергии.

В отношении величины gz это очевидно, ведь если частица жидкости массы m расположена на высоте z относительно некоторой плоскости и находится под действием сил тяжести, то способность ее совершить работу, т.е. её потенциальная энергия относительно этой плоскости равняется mgz. Но если её поделить на массу частиц m, то эта часть потенциальной энергии даст величину gz.

Для более ясного физического представления о том, что потенциальная энергия измеряется величиной p/ρ рассмотрим такую схему: пусть к трубе, заполненной жидкостью с избыточным давлением p, присоединен пьезометр, снабженный на входе в него краном.

Кран сначала закрыт, т.е. пьезометр свободен от жидкости, а элементарный объем жидкости ΔV массой ρ*ΔV перед краном находится под давлением p.

Если затем открыть кран, то жидкость в пьезометре поднимется на некоторую высоту, равную

Таким образом, единица массы, находящейся под давлением p, как бы несет в себе ещё заряд потенциальной энергии, определяемой величиной p/ρ.

В гидравлике для характеристики удельной энергии обычно используется понятие напор, под которым понимают энергию жидкости, отнесенную к единице силы тяжести, а не её массы. В соответствии с этим уравнение Бернулли записанное в начале этой статьи примет вид

Такое уравнение Бернулли для элементарной струйки идеальной жидкости в другой форме, весьма удобно для гидравлических расчетов и может быть сформулировано следующим образом.

Для элементарной струйки идеальной жидкости полный напор, т.е. сумма геометрического, пьезометрического и скоростного напоров, есть величина постоянная во всех её сечениях.

Отсюда следует, что между напором и удельной энергией существует очень простая зависимость

где э – удельная энергия

Уравнение Бернулли для элементарной струйки реальной жидкости

Если вместо идеальной жидкости рассматривать жидкость реальную, то уравнение Бернулли для реальной жидкости должно принять несколько другой вид.

При движении идеальной жидкости её полная удельная энергия или напор сохраняет постоянное значение по длине струйки, а при движении реальной жидкости эта энергия будет убывать по направлению движения. Причиной этого являются затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости.

Если же мы рассмотрим два сечения для струйки идеальной жидкости: 1-1 в начале и 2-2 в конце струйки, то полная удельная энергия будет

Полная удельная энергия для сечения 1-1 всегда будет больше, чем полная удельная энергия для сечения 2-2 на некоторую величину потерь, и уравнение Бернулли в этом случае получается

Величина Э_1-2 представляет собой меру энергии, потерянную единицей массы жидкости на преодоление сопротивлений при её движениями между указанными сечениями.

Соответствующий этой потере удельной энергии напор называют потерей напора между сечениями 1-1 и 2-2 и обозначают h_1-2 . Поэтому уравнение Бернулли для элементарной струйки реальной жидкости можно представить в виде

Уравнение Бернулли для потока реальной жидкости

Уравнение Бернулли для струйки реальной жидкости это еще только половина дела, ведь в при решении различных практических вопросов о движении жидкостей приходится иметь дело с потоками конечных размеров. Уравнение Бернулли в этом случае может быть получено, исходя из рассмотрения потока как совокупности множества элементарных струек.

Учитывая, что все струйки движутся с одной и той же средней скоростью форма записи уравнения Бернулли для потока идеальной жидкости становится идентичной его записи для элементарной струйки.

В таком виде уравнение Бернулли обычно и применяется при решении практических задач для потоков однородной несжимаемой жидкости при установившемся движении, происходящем под действием одной силы тяжести.

Такое уравнение составляется для различных живых сечений потока, вблизи которых движение жидкости должно удовлетворять условиям медленно изменяющегося движения, хотя на пути между этими сечениями движение может и не удовлетворять указанным условиям.

Слагаемое h_1-2 в этом уравнении показывает потери напора на преодоление сопротивлений движению жидкости. При этом в гидравлике различают два основных вида сопротивлений:
— h_лп — линейные потери — сопротивления, проявляющиеся по всей длине потока, обусловленные силами трения частиц жидкости друг о друга и о стенки, ограничивающие поток.
— h_мп — местные потери – местные сопротивления, обусловленные различного рода препятствиями, устанавливаемыми в потоке (задвижка, кран, колено), приводящими к изменениям величины или направления скорости течения жидкости

Поэтому полная потеря напора между двумя сечениями потока при наличии сопротивлений обоих видов будет

Видео по теме

Уравнение Бернулли подходит и для газов. Явление уменьшения давления при повышении скорости потока является основой работы различных приборов для измерения расхода. Закон Бернулли справедлив и для жидкостей вязкость которых равна нулю. При описании течения таких жидкостей используют уравнение Бернулли с добавлением слагаемых учитывающих потери на местные сопротивления.

Видео:Уравнение Бернулли гидравликаСкачать

Уравнение Бернулли для элементарной струйки и потока реальной жидкости

В отличие от идеальной жидкости при движении реальной жидкости часть энергии расходуется на преодоление гидравлических сопротивлений. Поэтому начальная общая энергия жидкости по длине струйки или потока уменьшается от сечения к сечению, т.е. гидромеханическая энергия преобразовывается в тепловую. Поэтому уравнение Бернулли для элементарной струйки реальной жидкости имеет вид:

где /?_п — называется потерянным напором.

В потоке реальной жидкости скорости в разных точках сечения потока не одинаковы вследствие действия силы трения, отсутствующей у идеальной жидкости. В результате происходит торможение у стенок сосуда. При этом сумма кинетических энергий элементарных струек ^ К, = ак_ср связана

с кинетической энергией потока, подсчитанной по средней скорости в данном сечении, коэффициентом Кариолиса а и уравнение Бернулли приобретает вид:

Для турбулентного течения в трубах а изменяется 1,02. 1,122.

Видео:Закон Бернулли в реальной жизниСкачать

Дифференциальные уравнения Эйлера движения невязкой жидкости

Дифференциальные уравнения равновесия Эйлера дают возможность установить напряжённое состояние неподвижной жидкости. Для движущейся жидкости необходимо получить связь действующих на неё сил не только с напряжениями, но и со скоростями. В теоретической механике известен способ использования уравнений статики для описания движения тел — принцип Даламбера. В соответствии с ним в исходные уравнения равновесия нужно ввести силы инерции

Все величины в уравнениях отнесены к массе жидкой частицы и имеют размерность ускорения. Поэтому и сила инерции должна быть также отнесена к массе частицы. Тогда она численно равна ускорению движения:

Проекции удельной силы инерции на соответствующие оси выражаются через компоненты скорости следующим образом:

Согласно принципу Даламбера, уравнения движения получают вид:

Эти уравнения справедливы для невязкой жидкости, так как при выводе исходных зависимостей не были учтены касательные напряжения.

Видео:Уравнение Бернулли для потока жидкостиСкачать

Уравнение движения Навье-Стокса

В реальных (вязких) жидкостях при движении обязательно появляются касательные напряжения трения, значение которых определяется законом вязкого трения Ньютона. Силы трения можно ввести в уравнение движения жидкости, отнеся их, как и все остальные слагаемые к массе жидкости. В итоге получаются дифференциальные уравнения движения жидкости Навье- Стокса (при р = const):

где v — кинематическая вязкость.

Решение уравнений Навье-Стокса является гораздо более сложной задачей, чем решение уравнений Эйлера. Отметим также, что система (9.5) является замкнутой.

Вопросы для самопроверки к разделу 9

1. Чем отличается жидкое тело от твёрдого и газообразного?
2. В чём состоит различие между удельным весом и плотностью?
3. Что называется вязкостью жидкости?
5. Что называется абсолютным, избыточным, вакуумметрическим давлением?
6. Какими свойствами обладает элементарная струйка жидкости?
7. Напишите уравнение Бернулли для двух сечений потока реальной жидкости и объясните геометрический и физический смысл каждого члена, входящего в это уравнение.
8. Какой физический смысл коэффициента Кориолиса «а»?
9. В чём различие между ламинарным и турбулентным режимами движения жидкости в трубах?

«Прикладная механика» является первой инженерной дисциплиной в учебном плане высшего технического учебного заведения по любой специальности. Изучая дисциплину, студенты знакомятся с примерами расчёта элементов конструкций на прочность, жёсткость. Приобретенные при этом знания в значительной степени облегчают усвоение последующих специальных дисциплин. В прикладной механике опыт и теория тесно увязаны между собой, наука эта является одновременно теоретической и опытной.

В ней широко применяются методы математического анализа, а также используются данные из разделов физики, в которых изучаются свойства различных материалов, поэтому приступать к изучению дисциплины можно только после изучения указанного материала.