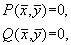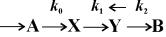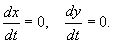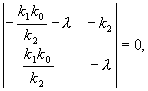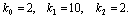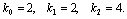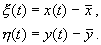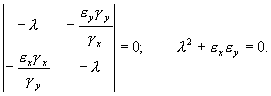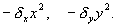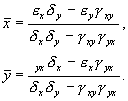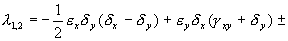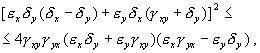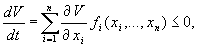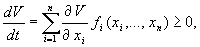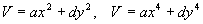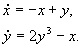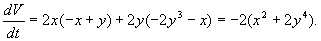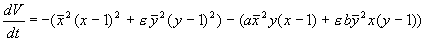Устойчивость стационарных систем из двух переменных линеаризованная система уравнений

Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Digiratory

Видео:Устойчивость 1 ОпределениеСкачать

Лаборатория автоматизации и цифровой обработки сигналов

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Устойчивость нелинейных систем

Анализ устойчивости систем является одним из важнейших этапов проектирования систем управления, однако при анализе нелинейных, строго говоря, нет метода отвечающего критериям необходимости и достаточности, а критерии являются, как правило только достаточным (для устойчивости). Исходя из этого, для некоторых систем невозможно однозначно говорить о неустойчивости.

В классической теории управления имеется два основных аналитических метода: первый и второй методы Ляпунова, а также достаточно большое количество модификаций второго метода, как не связанного с линеаризацией.

Рассмотрим применение классических методов Ляпунова.

Видео:Филиппов №881(г) — Исследование решения на устойчивостьСкачать

Первый метод Ляпунова

Позволяет судить об устойчивости положения равновесия по линеаризованным уравнениям. Метод основан на утверждениях:

• если собственные значения линеаризованной системы имеют отрицательные действительные части (линеаризованная система асимптотически устойчива), то положение равновесия нелинейной системы устойчиво «в малом»;
• если среди собственных значений линеаризованной системы имеются «правые», то положение равновесия нелинейной системы неустойчиво;
• если имеются некратные собственные значения на мнимой оси, а остальные — «левые», то в этом критическом случае по линеаризованной модели нельзя судить об устойчивости положения равновесия нелинейной системы.

Таким образом для анализа системы по первому методу Ляпунова необходимо:

1. Найти положение равновесия системы — движений в системе нет (т.е. скорости и ускорения равны нулю) [ frac <mathrmv_><mathrmt>= ]
2. Линеаризовать систему в окрестности точки равновесия
3. Записать полученное линеаризованное дифференциальное уравнение в матричной форме (составить матрицу А)
4. Составить характеристический полином линеаризованной системы: [ = ]
5. Найти корни характеристического полинома. По виду корней сделать заключение о характере процессов в системе.

Основными недостатками первого метода Ляпунова являются:

• Если имеется корень на мнимой оси, то невозможно сказать о поведении процессов в системе.
• Возможно говорить только об устойчивости «в малом», т.е. при больших отклонениях от положения равновесия система может быть неустойчивой.

Пример 1.

Исследуем систему описываемую дифференциальными уравнениями:

Шаг 1. Положение равновесия:

Для нахождения точек равновесия левые части уравнений приравниваются к 0, что эквивалентно тому, что переменные состояния являются константами, а все их производные равны 0.

Шаг 2. Линеаризация для малых отклонений

Для линеаризации малых отклонений в точке равновесия старшие степени переменных, входящих в уравнения принимаются равными нулю.

Шаг 3. Линеаризованное управление в матричной форме

Преобразуем полученную линейную систему уравнений в матричный вид.

Шаг 4. Характеристический полином

Шаг 5. Корни характеристического полинома

Приравниваем характеристический полином к 0 и находим корни уравнения.

Заключение об устойчивости системы

в данном примере при линеаризации система имеет два корня с отрицательной вещественной частью, т.е. мы можем сказать, что система устойчива «в малом» (при больших отклонениях система может быть неустойчива).

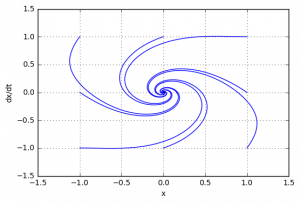
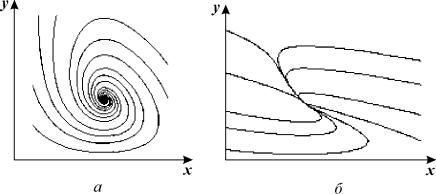
Подтвердим теоретический вывод компьютерным моделированием (построением фазового портрета)

При этом, при начальных условиях, находящиеся дальше от точки равновесия, система становится неустойчивой

Пример 2. Нелинейный осциллятор

В качестве второго примера рассмотрим нелинейный осцилятор описываемый системой дифференциальных уравнений:

Аналогично первому примеру выполняем последовательность шагов

Шаг 1. Положение равновесия:

Шаг 2. Линеаризация для малых отклонений

Шаг 3. Линеаризованное управление в матричной форме

Шаг 4. Характеристический полином

Шаг 5. Корни характеристического полинома

Заключение об устойчивости системы

Рассматриваемая система является критическим случаем о ее устойчивости невозможно судить по линеаризованным уравнениям, применяемым в первом методе Ляпунова.

Видео:Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 3.5. Линеаризация систем диф.уровСкачать

Второй метод Ляпунова

Второй метод Ляпунова не связан с линеаризацией системы, поэтому также называется прямым методом.

Для начала необходимо ввести понятия знакоопределенной, знакопостоянной и знакопеременной функций. Пусть имеется функция нескольких переменных:

Функция (V ) называется знакоопределенной в некоторой области, если она во всех точках этой области вокруг начала координат сохраняет один и тот же знак и нигде не обращается в нуль, кроме только самого начала координат

[ left ( Vleft ( bar right )=0 right ) ]

Функция (V ) называется знакопостоянной, если она сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках данной области.

Функция (V ) называется знакопеременной, если она в данной области вокруг начала координат может иметь разные знаки.

Теорема Ляпунова об устойчивости нелинейных систем

Если при заданных в форме

уравнениях системы n-го порядка можно подобрать такую знакоопределенную функцию Ляпунова

чтобы ее производная по времени

тоже была знакоопределенной (или знакопостоянной), но имела знак противоположный знаку (V), то данная система устойчива.

Для упрощения скажем, что функция Ляпунова должна быть положительной знакоопределенной функцией. Тогда условия теоремы Ляпунова будут выглядеть следующим образом:

Для устойчивости положения равновесия достаточно существования дифференцируемой функции

называемой функцией Ляпунова, удовлетворяющей в окрестности начала координат следующим условиям:

1. (Vleft ( v_, v_,…, v_right ) geq 0) причем (V=0) лишь при следующем условии, означающем что функция (V) имеет строгий минимум в начале координат. [ bar= begin v_ \ vdots \ v_ end = bar ]
2. Производная функции по времени [ frac <mathrmVleft ( bar right )><mathrmt>=sum_^frac<partial v_>frac <mathrmv_><mathrmt>=begin frac<partial v_> & frac<partial v_> & cdots & frac<partial v_>endbeginfrac <mathrmv_><mathrmt>\ frac <mathrmv_><mathrmt>\ vdots \ frac <mathrmv_><mathrmt>end ] в силу дифференциального уравнения (frac <mathrmbar><mathrmt>=barleft ( bar right ) ) является отрицательной знакопостоянной функцией, т.е. [ frac <mathrmVleft ( bar right )><mathrmt>=gradbarcdot frac <mathrmbar><mathrmt>=gradbarcdot barleft ( bar right )leq 0 ] при (tgeq t_)

Таким образом, условия:

1. (frac <mathrmVleft ( bar right )><mathrmt>leq 0) и функция (Vleft ( v_, v_,…, v_right ) ) является положительной знакоопределенной — это является достаточным условием устойчивости
2. (frac <mathrmVleft ( bar right )><mathrmt> ) — отрицательно определенная — это является достаточным условием асимптотической устойчивости.
3. (left | v right |rightarrow infty : frac <mathrmVleft ( bar right )><mathrmt>rightarrow infty ) — достаточное условие устойчивости «в целом».

Для анализа системы по второму методу Ляпунова необходимо:

1. Выбрать функцию Ляпунова от n переменных, где n- порядок системы.
2. Найти частные производные по переменным.
3. Вычислить производную функции по времени (frac <mathrmVleft ( bar right )><mathrmt>). Проанализировать полученный знак производной.

Из-за того, что второй метод Ляпунова не связан с линеаризацией, он считается универсальным. Однако он имеет ряд недостатков:

• Нет общих требований по выбору функции V
• Достаточный характер утверждения (если условия не выполняются, то об устойчивости ничего сказать нельзя, а можно посоветовать подобрать другую функцию (V ))

Пример 3. Нелинейный осциллятор

Проанализируем систему из примера (2).

Шаг 1. Функция Ляпунова

Для начала необходимо выбрать функцию Ляпунова от 2-х переменных (т.к. два вектора состояния):

Шаг 2. Частные производные

Шаг 3. Производная функции

Подставим в выражение значения исходя из ДУ:

Заключение об устойчивости системы

Исследовав систему первым методом Ляпунова мы не смогли сделать конкретный вывод об устойчивости системы, что позволил нам сделать второй метод Ляпунова. В результате мы можем сделать вывод, что система является асимптотически устойчивой.

Аналогично проверим с помощью моделирования:

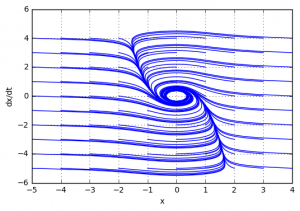
Пример 4.

Рассмотрим систему, описываемую следующей системой дифференциальных уравнений:

Очевидно, что применение первого метода Ляпунова невозможно, т.к. матрица А состоит из нулей, а, следовательно, собственные значения равны нулю. Поэтому применим второй метод Ляпунова:

Шаг 1. Функция Ляпунова

Выбор функции Ляпунова второго порядка

Шаг 2. Частные производные

Шаг 3. Производная функции

При (a=3) имеет место асимптотическая устойчивость.

Заключение об устойчивости системы

Система является устойчивой.

Фазовый портрет системы выглядит следующим образом:

Видео:Теория автоматического управления. Лекция 10. Критерий МихайловаСкачать

Устойчивость стационарных систем из двух переменных линеаризованная система уравнений

ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СТАЦИОНАРНЫХ СОСТОЯНИЙ НЕЛИНЕЙНЫХ СИСТЕМ ВТОРОГО ПОРЯДКА

Метод Ляпунова линеаризации систем в окрестности стационарного состояния. Примеры исследования устойчивости стационарных состояний моделей биологических систем. Уравнения Лотки. Уравнения Вольтерра. Метод функции Ляпунова

Пусть биологическая система описывается системой двух автономных дифференциальных уравнений второго порядка общего вида:

(5.1)

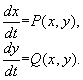
Стационарные значения переменных системы определяются из алгебраических уравнений:

(5.2)

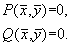
Стационарные состояния соответствуют особым точкам дифференциального уравнения первого порядка, определяющего интегральные кривые:

(5.3)

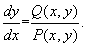
Математический анализ поведения траекторий этой системы на фазовой плоскости связан с именами французского математика Анри Пуанкаре и русского математика и механика Александра Михайловича Ляпунова (1857-1918).

Ляпунов показал, что в большом числе случаев анализ устойчивости стационарного состояния нелинейной системы можно заменить анализом устойчивости системы, линеаризованной в окрестности стационарного состояния.

Рассмотрим характер поведения переменных при некотором небольшом отклонении системы от состояния равновесия. Введем вместо переменных x, y новые независимые переменные x , h , определив их как смещения относительно равновесных значений переменных

(5.4)

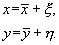
Подставив эти выражения в (5.1), получим:

(5.5)

, так как — координаты особой точки.

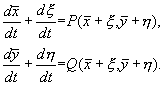
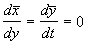
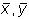
Предположим, что функции P и Q непрерывны и имеют непрерывные производные не ниже первого порядка. Тогда мы можем разложить правые части уравнений (5.5) в ряд Тейлора по переменным x , h .

(5.6)

(5.7)

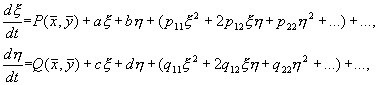
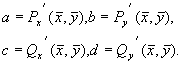
Учтем, что по определению особой точки

и отбросим в уравнениях (5.6) нелинейные члены. Получим систему линейных уравнений с постоянными коэффициентами — систему первого приближения:

(5.8)

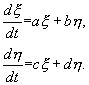
Решение этой системы было рассмотрено в Лекции 4. Оно определяется корнями характеристического уравнения системы:

(5.9)

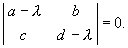
Ляпунов показал, что в случае, если оба корня уравнения (5.9):

(5.10)

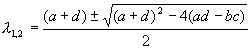
имеют отличные от нуля действительные части, исследование уравнений первого приближения (5.8) всегда дает правильный ответ на вопрос о типе устойчивости состояния равновесия в системе (5.1). А именно:

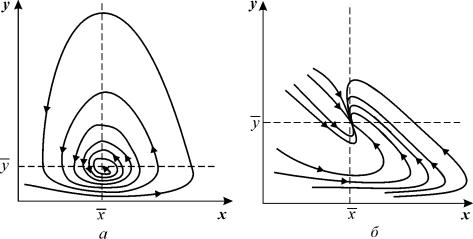
· если оба корня имеют отрицательную действительную часть и, следовательно, все решения уравнений первого приближения (5.8) затухают, то состояние равновесия устойчиво;

· если хотя бы один корень имеет положительную действительную часть, то есть система (5.8) имеет нарастающие решения, то состояние равновесия неустойчиво.

Если действительные части обоих корней характеристического уравнения равны нулю или если один корень равен нулю, а другой отрицателен, то уравнения (5.8) не дают ответа на вопрос об устойчивости состояния равновесия, и необходимо рассматривать члены более высокого порядка малости в разложении в ряд Тейлора правых частей уравнений (5.6).

В случае, когда оба корня характеристического уравнения имеют отличные от нуля действительные части ( грубые с истемы), уравнение первого приближения определяют не только устойчивость стационарного состояния, но и характер фазовых траекторий в достаточно малой его окрестности.

Как и в случае линейных уравнений (Лекция 4) здесь возможны пять типов грубых состояний равновесия: устойчивый узел, неустойчивый узел, устойчивый фокус, неустойчивый фокус и седло. Для исследования типов состояний равновесий удобно пользоваться диаграммой, изображенной на рис. 4.11. Для системы (5.1):

, (5.11)

. (5.12)

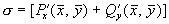
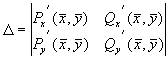
Грубым состояниям равновесия соответствуют все точки плоскости параметров s , D , лежащие вне оси D =0 и полуоси s =0, D >0.

Точкам оси D = 0 и полуоси s = 0, D >0 соответствуют негрубые состояния равновесия (негрубые особые точки). Их свойства могут быть изменены сколь угодно малыми изменениями правых частей уравнений (5.1) за счет сколь угодно малых изменений функций P(x,y), Q(x,y) и их производных. Поэтому характер негрубых состояний равновесия (в частности, устойчивость) уже не определяется значениями коэффициентов в правых частях уравнений первого приближения (5.8). В отличие от линейных систем, уже при небольших изменений в правых частях содержащихся там нелинейных членов может произойти качественное изменение фазового портрета — бифуркация.

1. Кинетические уравнения Лотки ( A . J . Lotka . Elements of Physical Biology, 1925)

Лоткой была исследована гипотетическая химическая реакция:

Модель очень простая и служит хорошей иллюстрацией применения исследования устойчивости стационарного состояния системы методом линеаризации.

Пусть в некотором объеме находится в избытке вещество А. Молекулы А с некоторой постоянной скоростью 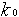превращаются в молекулы вещества X (реакция нулевого порядка). Вещество X может превращаться в вещество Y, причем скорость этой реакции тем больше, чем больше концентрация вещества Y – реакция второго порядка. В схеме это отражено обратной стрелкой над символом Y. Молекулы Y в свою очередь необратимо распадаются, в результате образуется вещество B (реакция первого порядка).

Запишем систему уравнений, описывающих реакцию:

(5.13)

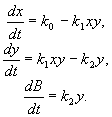
Здесь x , y , B — концентрации химических компонентов. Первые два уравнения этой системы не зависят от B , поэтому их можно рассматривать отдельно. Рассмотрим стационарное решение системы:

Из этих условий получим систему алгебраических уравнений, связывающих равновесные концентрации :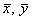

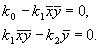
(5.14)

Координаты особой точки:

.

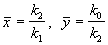
Исследуем устойчивость этого стационарного состояния методом Ляпунова. Введем новые переменные x , h , характеризующие отклонения переменных от равновесных концентраций :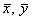

.

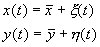
Линеаризованная система в новых переменных имеет вид:

(5.15)

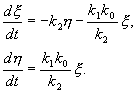
Отметим, что величины отклонений от стационарных значений переменных x , h могут менять знак, в то время как исходные переменные x , y , являющиеся концентрациями, могут быть только положительными.

Запишем характеристическое уравнение системы (4.3):

.

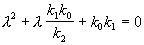
Корни характеристического уравнения:

.

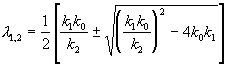
Фазовый портрет системы (5.13) изображен на рис. 5.1.

Рис. 5.1. Фазовый портрет системы 5.13.

а – устойчивый фокус ,

б – устойчивый узел.

При 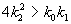подкоренное выражение отрицательно, и особая точка – фокус, при обратном соотношении – узел. И в том и в другом случае особая точка устойчива, так как действительная часть обоих корней характеристического уравнения отрицательна.

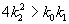
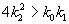
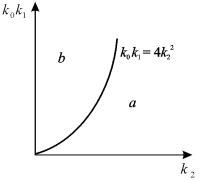
Таким образом, в описанной выше химической реакции возможны разные режимы изменения переменных в зависимости от соотношения величин констант скоростей. Если , имеют место затухающие колебания концентраций компонентов, при – бесколебательное приближение концентраций к стационарным.

Рис. 5.2 Плоскость параметров для системы 5.14.

а – область устойчивого фокуса; б – область устойчивого узла

Соотношение параметров 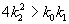соответствует изменению типа особой точки системы уравнений (5.13).

Рассмотрим плоскость параметров, где по оси абсцисс отложены значения константы k₂, а по оси ординат – произведение k ₀ k ₁ . Парабола k ₀ k ₁ = 4 k 2 ₂ делит изображенную на рис. 5.2 плоскость параметров на две области – устойчивых узлов и устойчивых фокусов. Задавая те или иные значения параметров, можно получить колебательный и бесколебательный режимы изменения концентраций веществ x и y , и фазовый портрет системы, соответственно, будет собой представлять фокус (а) или узел (б), изображенные соответственно на рис 5.1 а, и 5.1 б.

Если в системе установятся стационарные концентрации веществ x и y , это приведет к установлению постоянной скорости прироста концентрации вещества В в третьем уравнении системы (5.13):

.

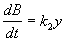
Ясно, что в действительности такая система реализоваться не может, так как в ней при t ® ¥ концентрация вещества В стремится к бесконечности. Однако система, подобная системе реакций Лотки, может представлять собой фрагмент более сложной химической системы. Исследованные нами уравнения правильно описывают поведение компонентов x и y , если приток вещества x (скорость его постоянна и равна k ₀ ) осуществляется из большого «резервуара», а отток вещества y – в большой «резервуар» (значение В очень велико). При этих предположениях на малых промежутках времени (по сравнению с временем существенного изменения заполненности емкости B ) наше рассмотрение является вполне правомерным.

2. Модель Вольтерра

В качестве второго примера рассмотрим классическую модель взаимодействия видов, которая впервые была предложена В. Вольтерра в тридцатые годы XX века для объяснения периодических изменений числа особей, так называемую вольтерровскую модель «хищник-жертва». Более подробно модели взаимодействия видов мы рассмотрим в Лекции 9.

Пусть в некотором замкнутом районе живут хищники и жертвы, например, зайцы и волки. Зайцы питаются растительной пищей, имеющейся всегда в достаточном количестве. Волки могут питаться лишь зайцами. Обозначим число зайцев (жертв) x, а число волков (хищников) – y . Так как количество пищи у зайцев неограниченно, мы можем предположить, что они размножаются со скоростью, пропорциональной их числу:

(5.16)

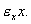
Если рождаемость зайцев превышает их смертность, e > 0. Выражение (5.16) соответствует автокаталитической реакции первого порядка.

Пусть убыль зайцев пропорциональна вероятности встречи зайца с волком, т.е. пропорциональна произведению численностей xy . Можно предположить по аналогии с бимолекулярными реакциями, где вероятность появления новой молекулы пропорциональна вероятности встречи двух молекул, что и количество волков нарастает тем быстрее, чем чаще происходят их встречи с зайцами, а именно, пропорционально xy .

Кроме того, имеет место процесс естественной смертности волков, причем скорость смертности пропорциональна их количеству.

Эти рассуждения приводят к системе уравнений для изменений численности зайцев-жертв x и волков-хищников y.

(5.17)

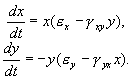
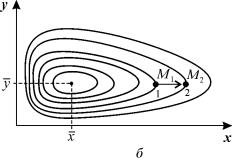
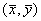
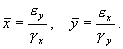
Покажем, что система уравнений (5.17) имеет на фазовой плоскости переменных xy ненулевую особую точку типа центр. Координаты этой особой точки легко найти, приравняв правые части уравнений системы (5.17) нулю. Это дает стационарные ненулевые значения:

.

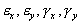
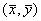
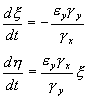
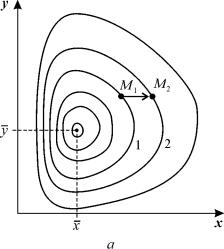
Так как все параметры положительны, точка расположена в положительном квадранте фазовой плоскости. Линеаризация системы вблизи этой точки дает:

(5.18)

Рис. 5.3. Фазовый портрет системы 5.17. Особая точка типа «центр».

а – параметры системы: e _x = 4, g _xy = 0,3, e _y = g _yx = 0,4

б – параметры системы: e _x =2, g _xy = 0,3, e _y = g _yx = 0,4

Здесь x , h — отклонения 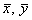численностей от их стационарных значений:

Характеристическое уравнение системы (5.18):

Корни этого уравнения чисто мнимые:

.

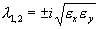
Таким образом, исследование системы показывает, что траектории вблизи особой точки являются концентрическими эллипсами, а сама особая точка – центром. Рас c матриваемая модель Вольтерра и вдали от особой точки имеет замкнутые траектории, хотя форма этих траекторий уже отличается от эллипсоидальной, и определяется параметрами системы (рис. 5.3).

Изменения численности жертвы и хищника во времени представляют собой колебания, причем колебания численности хищника отстают по фазе от колебаний жертв.

Как мы уже отмечали в Лекции 4, особая точка типа центр устойчива по Ляпунову, но не асимптотически. Покажем на данном примере, в чем это проявляется. Пусть колебания x ( t ) и y ( t ) происходят таким образом, что изображающая точка движется по фазовой траектории 1 (рис 5.3).

В момент, когда точка находится в положении М₁, в систему добавляется извне некоторое число особей y такое, что изображающая точка переходит скачком из точки M ₁ в точку M ₂ . Если после этого систему предоставить самой себе, колебания x ( t ) , y ( t ) уже будут происходить с большими амплитудами, чем прежде, и изображающая точка будет двигаться по траектории 2. Это и означает, что колебания в системе неустойчивы: они навсегда изменяют свои характеристики при внешнем воздействии.

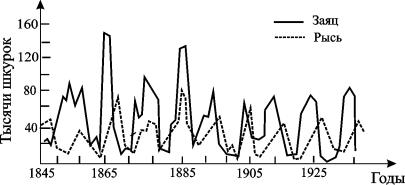
Рис. 5.4. Кривые численности зайца и рыси в Канаде

(по К. Вилли, В. Детье, 1974)

В дальнейшем мы рассмотрим модели, описывающие устойчивые колебательные режимы, и покажем, что на фазовой плоскости такие асимптотически устойчивые периодические движения описываются предельными циклами.

На рис. 5.4 кривые колебаний численности пушных зверей по данным компании Гудзонова залива о числе заготовленных шкурок. Во всех классических учебниках в течение многих лет колебательный характер этих изменений приводили как подтверждение гипотез, положенных в основу модели Вольтерра, которую мы только что рассмотрели. Действительно, периоды колебаний численности зайцев (жертв) и рысей (хищников) примерно одинаковы и составляют порядка 9 – 10 лет. При этом максимум численности зайцев опережает, как правило, максимум численности рысей на один год. Можно полагать, что мы видим регулярные колебания, осложненные случайными факторами, связанными с погодой и проч.

Однако возможна и другая интерпретация этих данных наблюдений на основе моделей детерминированного хаоса. О дискретных моделях такого типа мы уже говорили в Лекции 3. Непрерывные модели популяционной динамики, приводящие к детерминированному хаосу, мы рассмотрим в Лекции 9.

Серьезным недостатком рассмотренной модели Вольтерра является неустойчивость решений по отношению к малым случайным воздействиям, приводящим к изменению переменных. Кроме того, в силу «негрубости» этой системы произвольно малое изменение вида правых частей уравнений (величин параметров системы) приведет к изменению типа особой точки, и, следовательно, к изменению характера фазовых траекторий.

Поскольку природные системы подвергаются огромному количеству случайных воздействий, реалистическая модель должна быть по отношению к ним устойчивой. Поэтому негрубые системы не могут давать адекватное описание природных явлений.

Различные модификации рассмотренной нами системы, изученные самим Вольтерра и другими авторами, лишены этих недостатков. Наиболее широко известные из них будут рассмотрены в Лекции 9. Здесь мы остановимся на модели, которая учитывает самоограничение в росте обеих популяций. На ее примере видно, как может меняться характер решений при изменении параметров системы.

Итак, рассмотрим систему:

(5.19)

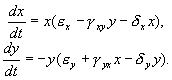
Система (5.19) отличается от ранее рассмотренной системы наличием в правых частях членов:

Эти члены отражают тот факт, что численность популяции жертв не может расти до бесконечности даже в отсутствие хищников в силу ограниченности пищевых ресурсов, ареала существования и проч. Такие же «самоограничения» накладываются на популяцию хищников.

Система имеет два стационарных решения: нулевое и ненулевое. Анализ показывает, что нулевое решение представляет собой неустойчивый узел. Рассмотрим систему алгебраических уравнений, решение которых дает координаты ненулевого стационарного состояния.

( 5 .20)

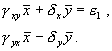
Корни характеристического уравнения системы, линеаризованной в окрестности особой точки:

.

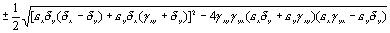
Из выражения для характеристических чисел видно, что если выполнено условие

то численности хищников и жертв совершают во времени затухающие колебания. Система имеет особую точку – устойчивый фокус.

Рис. 5.5. Фазовый портрет системы 5.19

а – устойчивый фокус,

б – устойчивый узел,

При изменении знака неравенства на обратный точка становится устойчивым узлом.

И в том и в другом случае стационарное состояние асимптотически устойчиво, и решение устойчиво к малым изменениям правых частей уравнений. Таким образом, самоограничение популяции приводит к устойчивости ее численности.

Важно отметить, что простейшие вольтерровские модели, которые мы рассмотрели, не могут описывать устойчивые колебания с постоянными периодом и амплитудой. Для описания таких колебаний необходимы нелинейные модели, имеющие на фазовой плоскости предельный цикл . Они будут рассмотрены в Лекции 8.

МЕТОД ФУНКЦИЙ ЛЯПУНОВА ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ СТАЦИОНАРНОГО СОСТОЯНИЯ.

При аналитическом исследовании устойчивости стационарного состояния часто используется метод подбора функции, линии уровня которой представляют собой замкнутые траектории – «ловушки» для фазовых траекторий системы типа (5.1)

Этот метод применим к автономной системе уравнений n -го порядка

(5.21)

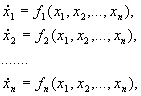
Он состоит в непосредственном исследовании устойчивости ее стационарного состояния при помощи подходящим образом подобранной функции Ляпунова .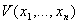

Метод основан на двух теоремах.

Если существует дифференцируемая функция V ( x ₁ ,…, x_n ), удовлетворяющая в окрестности начала координат следующим условиям:

б)

причем 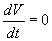лишь при x ₁ = … = x_n = 0 ,

то точка покоя системы (5.21) устойчива.

Если существует дифференцируемая функция V ( x ₁ ,…, x_n ), удовлетворяющая в окрестности начала координат следующим условиям:

a ) V ( x ₁ ,…, x_n ) = 0 и сколь угодно близко от начала координат имеются точки, в которых V ( x ₁ ,…, x_n ) > 0;

б)

причем 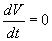лишь при x ₁ =…= x_n = 0,

то точка покоя системы (5.21) неустойчива.

С доказательством этих теорем можно познакомиться в книге Л.Э. Эльсгольц «Теория дифференциальных уравнений» или в других учебниках по теории дифференциальных уравнений.

Общего методы построения функции Ляпунова не существует. Однако для линейных автономных систем ее следует искать в виде:

и т.п., подбирая надлежащим образом коэффициенты a > 0 , b > 0. Для нелинейных систем a и b могут быть произвольных знаков.

1. Рассмотрим линейную систему:

Выберем функцию Ляпунова: V = x 2 + y 2 . Тогда

Это выражение всегда отрицательно при х ¹ 0 , т.к. в скобках стоят четные степени x . Следовательно, точка (0, 0) устойчива.

2. Рассмотрим систему уравнений, описывающую конкуренцию видов, численности которых x и y . Каждый из видов размножается в соответствии с логистическим законом, а при встрече (произведения в правых частях уравнений), численность как одного, так и другого вида уменьшается.

(5.22)

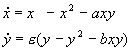
Исследуем стационарное состояние, соответствующее сосуществованию видов ( ` x , ` y ) – ненулевое для x и y . Его координаты:

. (5.23)

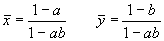
В. Вольтерра показал, что стационарное состояние (5.23) устойчиво для параметров системы a > 0, b £ 1 , построив функцию Ляпунова:

.

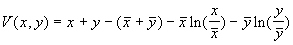
Ее производная равна

и отрицательна при малых значениях коэффициентов a , b и x , y > 0. Доказательство приведено в книге В. Вольтерра. «Математическая теория борьбы за существование» (М., 1976)

Ризниченко Г.Ю., Рубин А.Б. Математические модели биологических продукционных процессов. М., изд. МГУ, 1993

Вольтерра В. Математическая теория борьбы за существование М., Наука, 1976

Эльсгольц Л.Э. Теория дифференциальных уравнений. М., Наука, 1971

Видео:Устойчивость 5 Устойчивость по первому приближению Теорема ПримерыСкачать

Лекция 16 УСТОЙЧИВОСТЬ ОДНОРОДНЫХ СТАЦИОНАРНЫХ РЕШЕНИЙ СИСТЕМЫ ДВУХ УРАВНЕНИЙ ТИПА РЕАКЦИЯ-ДИФФУЗИЯ. ДИССИПАТИВНЫЕ СТРУКТУРЫ

1 Лекция 16 УСТОЙЧИВОСТЬ ОДНОРОДНЫХ СТАЦИОНАРНЫХ РЕШЕНИЙ СИСТЕМЫ ДВУХ УРАВНЕНИЙ ТИПА РЕАКЦИЯ-ДИФФУЗИЯ. ДИССИПАТИВНЫЕ СТРУКТУРЫ Линейный анализ устойчивости гомогенного стационарного состояния. Зависимость вида неустойчивости от волнового числа. Неустойчивость Тьюринга. Линейный анализ устойчивости гомогенного стационарного состояния распределенного Брюсселятора. Диссипативные структуры вблизи порога неустойчивости. Локализованные диссипативные структуры. Линейный анализ системы реакция-электродиффузия. Типы пространственно-временных режимов 1

2 Поведение распределенных систем из двух уравнений может быть чрезвычайно разнообразным. Здесь возможны распространяющиеся возмущения в виде бегущего импульса, генерация волн автономными источниками импульсной активности, стоячие волны, синхронные автоколебания во всем пространстве, квазистохастические волны и диссипативные структуры стационарные неоднородные распределения переменных в пространстве. Как и в случае точечных систем, важное место в изучении распределенных систем занимает исследование устойчивости стационарного состояния. Рассмотрим распределенную систему, в которой имеется два вещества, т.е. две кинетические переменные x и y, которые претерпевают химические превращения и кроме того могут диффундировать в реакционном объеме. В случае одномерного реактора такая система может быть описана системой уравнений: x x Pxyr (,, ) Dx, t r (16.1) y y Qxyr (,, ) Dy. t r Здесь r пространственная переменная. Пусть краевыми условиями являются условия непроницаемости торцов одномерного реактора: x r r0 x r rl y r r0 y r rl 0 (16.) Характер поведения такой системы со временем может быть различным. В простейшем случае при t во всех точках реактора установятся одинаковые концентрации x и y, т.е. система придет к своему устойчивому однородному в пространстве (гомогенному) стационарному состоянию. Если же однородное стационарное состояние неустойчиво, при t могут реализоваться другие режимы. Это либо другие однородные стационарные состояния, либо неоднородные стационарные (диссипативные) структуры. Возможно также, что в каждой точке пространства переменные с течением времени не стремятся к определенным значениям, а в системе устанавливается автоколебательный или квазистохастический режим. Таким образом, как и в случае точечных моделей, первым необходимым этапом изучения модели распределенной системы является исследование устойчивости ее однородного стационарного состояния. Рассмотрим пространственно однородное решение системы (16.1): x x Const; y y Const, (16.3) k k где x k и y k являются корнями алгебраической системы уравнений: P(x, y) = 0, Q(x, y) = 0 (16.4)

3 и, следовательно, являются особыми точками точечной системы. В лекции 14 мы рассмотрели устойчивость гомогенного стационарного состояния в случае одного уравнения. Такое состояние устойчиво, если малые возмущения сил (в том числе и распределенных в пространстве), действующих на систему, вызывают малые возмущения ее решений. Предполагается, что эти возмущения остаются малыми при любом t. Как и в случае одного уравнения, исследование устойчивости будем проводить на основе анализа линеаризованной системы уравнений. Пусть k (t, r) и k (t, r) малые отклонения от пространственно однородных решений x k и y k. Тогда для k и k можно записать распределенную линеаризованную систему (нижние индексы k для краткости опускаем): a b D t c d D t r,. r (16.5) Здесь, как и в лекциях 4, 5: P( x, y) P( x, y) a, b, x y Qxy (, ) Pxy (, ) c, d x y, Коэффициенты диффузии: D x = D, D y = D. (16.6) Решение будем искать в виде: pt ikr pt ikr (, tr) Ae e, (, tr) Be e. (16.7) Здесь множитель e ikr характеризует отклонение величин переменных от однородного стационарного состояния в точке с координатой r для собственных функций, соответствующих волновому числу k. Для трубки длиной l, как показано, в лекции 14, n волновое число принимает дискретные значения k kn. Множитель e pt l характеризует поведение отклонения от стационарного состояния во времени. Подстановка выражений (16.7) в (16.5) после сокращения на e pt e ikr дает: Ap = aa + bb D k A, Bp = ca + db D k B, (16.8) или: A(p a + D k ) bb = 0, ca (p d + D k )B = 0. (16.9) 3

4 Величины A, B тождественно не равны нулю только в том случае, если определитель системы (16.9) равен нулю: (p a + k D )(p d + k D ) bc = 0. (16.10) Уравнение (16.10) называется дисперсионным уравнением. Его решения: p 1, ad ( D D) k [ ad k ( D D)] 4bc. (16.11) Итак, мы получили выражение для величин p 1,, определяющих поведение системы во времени, через параметры системы и волновое число k. Как и в случае точечных систем, знак действительной части p 1, показывает, устойчивым или неустойчивым будет исследуемое однородное стационарное решение. В области параметров, где оба Re p 1, 0 неустойчивость типа фокуса и, наконец, если p 1 и p имеют разные знаки неустойчивость типа седла. 4

5 Рис Различные типы зависимости действительной части корней дисперсионного уравнения от волнового числа k. k 1 волновое число, при котором система становится устойчивой к данному виду возмущений; k система теряет устойчивость к данному виду возмущений; k 3 переход из области колебательной неустойчивости в область устойчивых колебаний; k 4 переход колебательной системы в бесколебательную; k 5 переход из области неустойчивого узла в область седловой неустойчивости (Адаптировано из Романовский и др., 004) На рис 16.1 изображены возможные виды зависимости действительной части p 1, от волнового числа k. На всех графиках можно выделить три области: I оба корня имеют положительную действительную часть, Re p 1, > 0. II один корень имеет положительную, а другой отрицательную действительную часть: Re p 1 > 0, Re p 6 характеристические числа p 1, комплексно сопряженные, и потому их действительные части равны, и область, где оба числа p 1, действительны и различны. На рисунках указаны значения волнового числа, которые соответствуют изменению типа устойчивости системы. Рассмотрим, какие изменения могут происходить при увеличении числа k. Величина k 1 соответствует значению, при котором один из вещественных корней (больший) переходит из положительной в отрицательную область, это соответствует переходу из области седловой неустойчивости (два положительных действительных корня разных знаков) II в область устойчивого узла III (рис. 16.1а,б,г. Величина k, наоборот, соответствует переходу из области устойчивого узла III в область седловой неустойчивости II (рис. 16.1г,д). Величина k 3 соответствует переходу из области колебательной неустойчивости I (Re p 1 = Re p >0) в область устойчивых колебаний: Re p 1 = Re p 7 поступают таким же образом, как и при исследовании систем второго порядка. Пусть координаты особой точки системы: x, x. x, ( m. M) (16.14) 1m m nm 1 где m номер особой точки. Возмущение представляется в виде суперпозиции волн вида: k x im xi xim im exp( pmkt j r), (16.15) l l где k волновое число, определяющее длину волны: mk, l длина трубки. k Подставляя (16.15) в линеаризованную систему уравнений, записанную в системе координат с началом в m-й особой точке и используя условие существования нетривиальных решений такой системы, получим дисперсионное уравнение, связывающее комплексные частоты p mk = mk jw mk, длины волн mk (волновые числа k) и коэффициенты системы q i (i = 0, n 1) (16.13): n n1 p q ( k ) p. q ( k ) 0. (16.16) mk n1 mk 0 Если исследуемое стационарное состояние неустойчиво, имеется хотя бы одно значение комплексной частоты p mk, для которой Re p mk > 0. Число корней дисперсионного уравнения с положительной действительной частью определяет тип неустойчивости системы. Если имеется четное число корней p mk с > 0, неустойчивость называют колебательной. Нечетному числу таких корней соответствует неустойчивость Тьюринга, приводящая к образованию стационарных неоднородных структур, названных диссипативными структурами (ДС). Этот термин подчеркивает термодинамический аспект проблемы ДС рождается и существуют в термодинамически открытых системах за счет диссипативных процессов утилизации энергии и энтропии (Николис и Пригожин, 1979). Неустойчивость Тьюринга Изучение нарушений симметрии системы имеет особенно важное значение для биологии. Действительно, самопроизвольный переход от однородного к пространственно неоднородному стационарному состоянию означает рождение в системе собственной структуры. Таким образом, исследование условий возникновения и регуляции диссипативных структур может пролить свет на процессы формообразования в организме, проходящие в соответствии с заложенной в геноме информацией. Основополагающая работа Тьюринга, в которой впервые были получены условия существования устойчивых неоднородных структур, была написана в 195 г. и называется «Химические основы морфогенеза». В работе рассмотрена общая система (16.1), 7

8 описывающая взаимодействие и диффузию химических веществ. Такая система, первоначально находившаяся в однородном стационарном состоянии, в дальнейшем может образовать структуру благодаря потере устойчивости однородного стационарного состояния. Пусть система представляет собой некий объем, заполненный клетками, которые вырабатывают и выделяют в среду химические вещества. Переход такой системы в пространственно неоднородное состояние может служить предпосылкой к разному типу функционирования клеток, находящихся в разном химическом окружении к их дифференцировке. Таким образом, химическая «предструктура» будет проявлена в биологической форме клеток разного типа. Осуществится дифференцировка клеток и морфогенез. При этом предполагается, что точечная кинетика изучаемых моделей физически реализуема, т.е. точечная система не имеет никаких неограниченно нарастающих решений. А. Тьюринг (Turing, 195) предложил два условия существования диссипативных структур: 1) стационарное состояние точечной системы является устойчивым фокусом (для модели с двумя переменными); ) имеется интервал значений волновых чисел (k min, k max ) при которых дисперсионное уравнение имеет два действительных корня с разными знаками. Если эти условия выполняются, то зависимость Re p mk от k имеет вид, представленный на рис Рис Зависимость действительной части корней дисперсионного уравнения Re p от волнового числа k в случае неустойчивости Тьюринга 8

9 Анализ дисперсионного уравнения (16.1) показывает, что устойчивое в отсутствие диффузии однородное состояние системы может стать неустойчивым, если выполняются следующие условия: ad bc 0, a d 0, Da D1d D1D ( ad bc). Выполнение первых двух неравенств обеспечивает отрицательность действительных частей собственных значений λ при k = 0 (k волновое число) устойчивость локальной системы в отсутствие диффузии. Выполнение третьего неравенства означает, что в некотором диапазоне волновых чисел одно из собственных значений становится положительным, т.е. однородное состояние теряет устойчивость относительно соответствующих длин волн. Принципиально важно, что неравенства могут выполняться одновременно, только если один из коэффициентов на главной диагонали, например, a положителен, тогда соответствующая переменная x является автокаталитической и часто называется «активатором», а коэффициент диффузии второй переменной y «ингибитора», существенно больше коэффициента диффузии активатора: D y > D x. Таким образом, А.Тьюринг, увидел в уравнениях (16.1) принципиальную возможность описания морфогенеза. В течение последующих 30 лет появились многочисленные работы (Murray, 1993; Mainhardt, 1999), в которых с помощью уравнений такого типа описывали раскраску шкур животных, образование структур морских звезд и раковин и многое другое. Мы рассмотрим эти модели в лекции 19. Конечно, моделирование образования столь сложных структур невозможно без компьютерной техники. Романо вский Юрий Михайлович русский советский физик, биофизик, профессор Физического факультет МГУ, специалист в области автоволновых процессов в физических, химических и биологических системах, динамических моделях белка, автор классических книг по математической биофизике (Романовский, Степанова, 9

10 Чернавский, 1976, 1984, 004) Романовским и Васильевым (Васильев и Романовский, 1976) были получены более общие условия: если свободный член дисперсионного уравнения отрицателен при некотором значении волнового числа k(q 0 (k) 11 длины L t больше. С термодинамической точки зрения переключение ДС и деление системы надвое приводит к уменьшению производства энтропии в системе и уменьшению диссипации энергии. В системах с двумя переменными колебательная неустойчивость для волн конечной длины может существовать лишь когда соответствующая точечная система является автоколебательной. В то же время неустойчивость Тьюринга может возникнуть даже если стационарное состояние точечной системы устойчиво (такая ситуация невозможна для системы с одной переменной). Если точечная система является автоколебательной, то всегда возможны такие значения коэффициентов диффузии, при которых имеет место неустойчивость Тьюринга. В системах с тремя и более переменными возможны случаи когда, несмотря на автоколебательный характер точечной системы, неустойчивость Тьюринга невозможна ни при каких значениях коэффициентов диффузии. В то же время в таких системах может возникнуть колебательная неустойчивость, хотя точечная система не является автоколебательной. В случае, когда имеет место взаимная диффузия компонентов, разнообразие систем, в которых возможны неустойчивости однородного состояния, еще более увеличивается. В частности, точечные системы в этом случае могут быть устойчивы при любых значениях параметров. В двумерных и трехмерных системах разнообразие возможных пространственновременных режимов многократно возрастает. Пример. Распределенный брюсселятор В лекции 8 мы рассмотрели простейшую модельную автоколебательную систему «брюсселятор», описывающие химическое взаимодействие двух веществ по схеме, включающей реализацию кубической нелинейности: X + Y 3X. Посмотрим, каким может быть пространственно-временное поведение системы, если в каждой точке локальное взаимодействие описывается уравнениями типа «брюсселятор» (8.6). Пусть реакции протекают в узкой длинной трубке (одномерном реакторе), вдоль которой вещества могут диффундировать. Коэффициенты диффузии D x, D y будем считать постоянными параметрами системы. Концы трубки, так же как и ее стенки, непроницаемы 11

12 для веществ, участвующих в реакции. Уравнения, описывающие распределенный брюсселятор, имеют вид: X t Y t X r A X Y ( B 1) X D, x Y BX X Y D, y (16.17) r (r пространственная координата). Напомним, что для точечной системы имеется одно стационарное состояние, которое характеризуется значениями концентраций: B X A, Y. A Такими будут концентрации во всех точках реактора, если гомогенное стационарное состояние системы устойчиво. Для исследования условий потери устойчивости однородного по пространству решения введем переменные, характеризующие малые отклонения системы от однородного решения (16.18): B X A, Y. A Линеаризуем систему (16.17), и решение линеаризованной системы будем искать в виде: (, tr) (, tr) Ce Ce ptikr 1 ptikr Величины p и k связаны дисперсионным уравнением типа (16.10), которое позволяет определить характер устойчивости исследуемого гомогенного решения. Дисперсионное уравнение для брюсселятора имеет вид: (p B 1 + k D )(p + A + k D ) + BA = 0 (16.18) Если уравнение (16.18) имеет два действительных корня, причем один из них p 1 0, то система в области гомогенного стационарного решения имеет неустойчивость седлового типа (неустойчивость Тьюринга). Условия существования такой неустойчивости выполняются при Dy ( 1 B) B1, Dx. (16.19) A Границы области волновых чисел k, в которой реализуется неустойчивость Тьюринга, даются выражением: 1 k B D D A B D D A A D D. (16.0) 1, ( 1) y x ( 1) y x 4 x y DD x y 1

13 Именно в этой области система (16.17) образует диссипативные структуры. Аналитическое исследование устойчивости неоднородных стационарных решений представляет значительные трудности, и в основном для этой цели используют асимптотические методы. Так, устойчивость диссипативных структур в брюсселяторе исследовали методом малых возмущений, предполагая, что диссипативная структура носит квазигармонический характер (Васильев и Романовский, 1976). Стационарные решения представляли в виде: x() r a a cos( kr); y() r b b cos( kr) c sin( kr), а малые возмущения в виде: 1 1 n (, tr) j ()cos( t jkr), ( tr, ) j ( t)(cos jkr). j0 n j0 Показано, что при k min 14 Локализованные диссипативные структуры Описанные выше диссипативные структуры распространяются на всю систему. Этот факт является следствием предположения о том, что концентрации исходных веществ реакций A и B поддерживаются постоянными во всех точках пространства. Такая ситуация является идеализированной. В реальном эксперименте реагенты вводятся в реакционный объем через границы. Это означает, что вещества A и B будут диффундировать в среде, что приведет к установлению их концентрационных профилей. Неоднородное пространственное распределение исходных веществ приводит к локализации диссипативных структур внутри определенных границ. В случае, когда вещество B равномерно распределено по объему, а концентрация вещества A поддерживается постоянной на границе, систему уравнений (16.17) следует дополнить уравнением, описывающим потребление и диффузию вещества А. Получим систему из трех уравнений: X X A X Y ( B1) X Dx, t r Y Y BX X Y Dy, t r, (16. 1) A A ADA, t r (0 r l) и граничными условиями: A() 0 A() l A. Концентрационные профили вещества Х, полученные в соответствии с системой (16.1) для разных значений параметра В, представлены на рис

15 Рис Локализованная диссипативная структура, полученная при численном решении системы (16.1) для последовательно увеличивающихся значений параметра В. На границах поддерживались значения переменных, соответствующие гомогенному стационарному состоянию. Параметры системы: D А = 0.06, D x = , D y = , l = 1; а B = 7; б B = 1; в B = 5 (Николис и Пригожин, 1979) Пространственно-временные режимы в системе реакция-электродиффузия Участие заряженных молекул в большинстве химических и биологических процессов обуславливает необходимость принимать во внимание вклад так называемого самосогласованного поля (электрического поля, возникающего в результате движения и взаимодействия заряженных частиц) в различные динамические режимы. В живых организмах роль ионов очевидна. Среди наиболее значимых для клетки процессов с участием ионов создание градиентов трансмембранного потенциала и движение электрического импульса. Эти процессы играют основную роль в проведении нервного импульса (лекция 18) и образовании структур рн вдоль клеточных мембран (лекция 19). Исследование механизмов таких явлений требует не только изучения работы конкретных механизмов каналов и переносчиков, но и понимания динамики в целом, то есть изучения организации пространственно-временных явлений с учетом самосогласованного поля. Существует два основных подхода к описанию электрических явлений на мембранах и вблизи мембран. Первый подход использование эквивалентных электрических схем, мы воспользуемся этим подходом в лекциях 18, 19. Другой подход 15

16 использование уравнения электродиффузии. В сочетании с химическими реакциями уравнения электродиффузии применяли, в основном, для описания воздействия внешних электрических полей (Munster et al., 1994; Sevikova et al., 1996) При этом выдвигались предположения об электронейтральности как следствии высокой ионной силы растворов. Такие предположения, справедливые для химических сред, позволяли значительно упростить анализ задач. Однако применительно к биологическим средам эти предположения справедливы не всегда. Так, вблизи клеточных мембран электронейтральность может быть нарушена в результате активного транспорта ионов, существования двойного электрического слоя и фиксированных зарядов на белковых молекулах, встроенных в мембрану. Покажем на простой модели (Плюснина и др., 00), что учет самосогласованного поля в системах с нелинейной химической кинетикой может приводить к биологически значимым эффектам, связанным с перераспределением зарядов и созданием градиентов потенциала. Лоба нов Алексе й Ива нович доктор физико-математических наук, профессор Московского физико-технического Института (госуниверситет). Специалист в области математического моделирования в биологии и медицине, в динамике высокотемпературной плазмы, численных методах. Автор более 150 научных и учебнометодических работ. Уравнения реакция-электродиффузия для концентрации двух типов ионов вблизи клеточной мембраны Рассмотрим систему, в которой помимо нейтральных присутствуют заряженные частицы. Это могут быть, например, ионы, находящиеся вблизи клеточной мембраны, диффундирующие вдоль нее и вступающие в химические реакции. Будем считать, что концентрация ионов много ниже концентрации нейтральных молекул, т.е. рассматривается раствор с низкой ионной силой. Изменения концентраций разных видов ионов описываются системой реакцияэлектродиффузия, которая для одномерного случая имеет вид: 16

17 ni t Ji x f ( n ), (16.) i RTui ni Ji nu i iz i F x x, (16.3) где потоки компонентов J i описываются уравнением Нернста-Планка, n i концентрация i вида ионов, f(n i ) нелинейная функция, описывающая изменение концентрации ионов за счет происходящих на мембране химических реакций, u подвижность иона, z валентность, Т абсолютная температура, R газовая постоянная, F число Фарадея, напряженность самосогласованного поля, сформированного зарядами ионов. Потенциал самосогласованного поля находится из уравнения Пуассона x 4F zn i i, (16.4) 0 i где диэлектрическая постоянная среды, 0 диэлектрическая проницаемость вакуума. Тогда для двух типов ионов (положительного n 1 и отрицательного n ) получим систему, которую после приведения к безразмерному виду можно записать как: с c c r r r D1 B1 B 1c1 c1z c f c1, c с c c r r r D B B c c1z c g c1, c c z c r 1 n1 n Здесь: c1, c, n n 01 0 t, t 0 x r, L 0 (16.5 а) (16.5 б) (16.5 в). x RT RTu10 t RTut0, 0, D1, D, Fz FL FL uzt uzt 00 B1, B 1, n 01 и n 0 характерные концентрации соответственно L L положительных и отрицательных ионов, t 0 характерное время, выражающееся через константы химических реакций. L размер рассматриваемой области, D 1 и D безразмерные коэффициенты диффузии положительных и отрицательных ионов, B 1 и B n0 подвижности ионов в электрическом поле. отношение характерных n z концентраций ионов, z отношение валентностей ионов, z F z1l n01 ; f(c 1, c ), RT g(c 1, c ) функции, задающие характер химического взаимодействия между ионами. В качестве граничных условий для уравнений, описывающих изменение 0 17

18 концентраций, будем рассматривать условие отсутствия потока частиц через границы области: J J J 0, 1, 0, (16.6 а) 1 1 J 0, 1, 0. (16.6 б) В качестве начальных условий выберем условие стационарного, однородного распределения концентраций, то есть решение алгебраической системы f(с 1, с ) = 0 и g(с 1, с ) = 0. Для уравнения Пуассона поставим граничные условия 0, 1, 0. (16.6 в) Условия (16.6) означают отсутствие внешнего электрического тока, направленного вдоль поверхности мембраны, а основное изменение потенциала происходит в примембранном слое, толщина которого примерно равна дебаевскому радиусу задачи. При этом на малых масштабах может протекать электрический ток, связанный с перераспределением ионов вдоль мембраны. Анализ системы по линейному приближению Итак, система (16.5) с граничными условиями (16.6) описывает электродиффузию и химическую реакцию двух типов ионов. Изначально такая система находится в устойчивом состоянии, в котором распределение концентраций однородно. В линейном приближении системы (16.6) члены, описывающие подвижность ci ионов за счет самосогласованного поля Bi исчезают, так как носят принципиально r r квадратичный характер. При линейном анализе можно говорить лишь о той составляющей, которая дает вклад в реакционную часть за счет уравнения Пуассона B c c z c i i i j Исследуя устойчивость стационарного состояний c 1 и c относительно небольших отклонений u(r, t) = Aе +ikr, v(r, t) = Bе +ikr, получим дисперсионное уравнение a Dk a D k a a (16. 7) , где с учетом с1 z c 0, f c, c a Bc, a c1 g c, c 1 1 c1 B z c, f c, c a B z c c1 g c, c a z B c. 1 c1 18

19 Видно, что коэффициенты матрицы линеаризации содержат добавочные члены, выражающие влияние самосогласованного поля. Значения параметров можно подобрать так, что без учета вклада поля система будет устойчива по Тьюрингу (рис.16.5а), а с учетом поля в системе возникают структуры (рис.16.5б). Рис а затухание возмущения в системе без учета самосогласованного поля в области параметров вблизи бифуркации Тьюринга. Параметры системы: D 1 = , D = , B 1 = B = 0, z = 0.5, = 0., = 1; б возникновение структур в системе с учетом самосогласованного поля. Параметры системы: D 1 = , D = , B 1 = 0.01, B = 0.035, z = 0.5, = 0., = 1 (Плюснина и др., 00) При определенных условиях амплитуда структур может отличаться в центре области и вблизи границ, например, уменьшаться к границам области (рис.16.5б). Таким образом, учет самосогласованного поля дает поправку в условия возникновения тьюринговской неустойчивости. При увеличении подвижности ионов в самосогласованном поле в системе возникает нерегулярная, квазихаотическая динамика (рис.16.6а). При определенных начальных условиях может также возникнуть структура типа двойного слоя, которая движется от одной границы области до другой, не изменяя своей формы (рис.16.6б). 19

20 Рис а нерегулярная, квазихаотическая динамика. Параметры системы: D 1 = , D = , B 1 = 0.1, B = 0.35, z = 0.5, = 0., = 1; б структуры типа двойного слоя. Параметры системы: D 1 = D = 10 4, B 1 = B = 0.04, z = 1, = 1, =1 (Плюснина и др., 00) Нужно заметить, что в рассматриваемой области параметров система обладает высокой чувствительностью к начальным данным. Существует лишь небольшой набор начальных условий, при которых обнаруживаются структуры. Возможно, такие структуры могут играть роль в передаче информации в биологических системах, поскольку способны двигаться длительное время, не изменяя своей формы. Качественно появление таких структур напоминает прохождение электрического импульса, описанного для нервных и растительных клеток. Появление таких импульсов в примембранном слое, по-видимому, представляет собой один из альтернативных механизмов образования и распространения потенциала действия. Литература Meinhardt H. The algorithmic beauty of sea shells. Berlin, Springer-Verlag, 1995 Munster A.F., Hasal P., Snita D.,Marek M.. Charge distribution and electric field effects on spatiotemporal patterns. Phys. Rev. E 50 (1): , 1994 Murray J.D. Mathematical biology. Berlin, Springer-Verlag, 1993 Sevikova H., Kosek J., Marek M. Splitting of D waves of excitation in a direct current electric field. J. Phys. Chem. 100(5): , 1996 Turing A.M. The chemical basis of the morphogenesis. Phil. Trans. R. Soc. London B 37: 37-71, 195 Васильев В.А. и Романовский Ю.М. О роли диффузии в системах с автокатализом. В: Теоретическая и экспериментальная биофизика, т. 6, с. 73. Калининград, 1976 Котык А. и Янычек К. Мембранный транспорт. М., Мир, 1980 Николис Г. и Пригожин И.Р. Самоорганизация в неравновесных системах: От диссипативных структур к упорядоченности через флуктуации. М., Мир, 1979 Плюснина Т.Ю., А.И.Лобанов, А.И.Лаврова, Т.К.Старожилова, Г.Ю.Ризниченко. А.Б.Рубин. Новые пространственно-временные режимы в системе реакция-электродиффузия. Биофизика, 47, 77-8, 00 Плюснина Т.Ю., Лобанов А.И., Лаврова А.И., Старожилова Т.К., Ризниченко Г.Ю., Рубин А.Б. Влияние электрического поля на динамику ионов вблизи клеточной мембраны. В: «Математика. Компьютер. Образование. Сборник тезисов», вып. 9, с М.-Ижевск, ИКИ-РХД, 00 Романовский Ю.М., Степанова Н.В., Чернавский Д.С. Математическое моделирование в биофизике. М., Наука, 1975 Романовский Ю.М., Степанова Н.В., Чернавский Д.С. Математическая биофизика. М., Наука,

21 Романовский Ю.М., Степанова Н.В., Чернавский Д.С. Математическое моделирование в биофизике. Введение в теоретическую биофизику. М-Ижевск, ИКИ-РХД, 004 1

💥 Видео

Видеоурок "Системы дифференциальных уравнений"Скачать

Системы дифференциальных уравнений. Часть 2Скачать

Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

9 класс, 8 урок, Уравнения с двумя переменнымиСкачать

Решение системы неравенств с двумя переменными. 9 класс.Скачать

После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

Системы неравенств с двумя переменными. Алгебра, 9 классСкачать

1) ТАУ (Теория автоматического управления) для чайников. Часть 1: основные понятия...Скачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Модели, представленный системой двух дифференциальных уравненийСкачать

Решение системы линейных уравнений с двумя переменными способом сложения. 6 класс.Скачать