Устойчивость решения разностного уравнения теорема о сходимости к точному решению (3 видео)

Содержание

Аппроксимация, устойчивость, сходимость разностных схем. Основные понятия
Сходимость. Аппроксимация. Устойчивость
Устойчивость и сходимость разностных методов
💡 Видео

Видео:Устойчивость 1 ОпределениеСкачать

Аппроксимация, устойчивость, сходимость разностных схем. Основные понятия

Рассмотрим некоторую задачу, определяемую дифференциальным уравнением и граничными условиями. Запишем ее в операторной форме

где через L обозначен некоторый дифференциальный оператор, действующий на искомую функцию и, через f — правая часть. Примем, что оператор L включает как дифференциальные уравнения, так и граничные условия. На некоторой разностной сетке строим разностный оператор L_h, действующий на сеточную функцию u_h. Примером дифференциального оператора является оператор Лапласа Д, а соответствующий ему разностный оператор возникает при аппроксимации вторых производных разностными отношениями (4.9) и (4.10).

Величина 6/_А называется НЕВЯЗКОЙ, и при подстановке точного решения уравнения (4.21) в оператор L_h имеем

РАЗНОСТНАЯ СХЕМА называется АППРОКСИМИРУЮЩЕЙ на решении, если норма невязки стремится к нулю при стремлении к нулю шага разностной схемы, т. е. ||б/_А|| -» 0 при h -» 0.

Если при этом постоянная С_р не зависит от шага h и норма невязки удовлетворяет условию ||5/J| р , то говорят, что разностная схема имеетр-й порядок аппроксимации или разностная схема аппроксимирует дифференциальный оператор с порядком р. Например, разностный оператор

аппроксимирует оператор Лапласа Д — т—т + —- со вторым по-

РАЗНОСТНАЯ СХЕМА называется СХОДЯЩЕЙСЯ, если норма разности точного и приближенного решений ||u — н_А|| стремится к нулю при стремлении к нулю шага разностной сетки.

Если при этом ||и — н_А[| p , где С_р — постоянная, не зависящая от шага Л и входных данных f.

Видео:6.3 Решение разностных уравненийСкачать

Сходимость. Аппроксимация. Устойчивость

Эти основные понятия теории разностных схем уже обсуждались при построении численных методов для решения обыкновенных дифференциальных уравнений. При переходе к уравнениям с частными производными качественно меняется характер рассматриваемых задач, поэтому необходимо снова рассмотреть эти понятия. Разумеется, мы не имеем здесь возможности изложить теорию разностных схем, но попытаемся привести самые необходимые сведения.

Исходную дифференциальную задачу,состоящую в решении уравнения с частными производными при заданных начальных и граничных условиях, запишем в операторном виде:

(2.7)

Заметим, что это операторное уравнение включает не только исходное уравнение с частными производными, но и дополнительные (начальные и граничные) условия. Функция F(x, t) описывает правые части уравнения, а также начальные и граничные условия. Область включает расчетную область Gи границу Г.

Дифференциальную задачу (2.7) заменяем разностной задачей относительно сеточной функции uh, определенной в узлах сетки . Для простоты будем считать, что сетка зависит от одного параметра h, а шаг по времени τ выражается через h: τ = rh, где r = const. Разностную задачу можно также записать в операторном виде:

(2.8)

Значения сеточной функции в узлах сетки приближенно заменяют значения искомой функции в тех же узлах с погрешностями:

(2.9)

Введем некоторое характерное значение этих погрешностей, например их максимальное по модулю значение на сетке

Разностная схема (2.8) называется сходящейся,если при сгущении узлов сетки это значение погрешности стремится к нулю, т.е. если

Если при этом , где М = const > 0, то разностная схема имеет k—ый порядок точности. Говорят также, что она сходится со скоростью O(hk).

Можно ввести понятие порядка точности и для случая независимых параметров сетки h, τ. В частности, при выполнении условия разностная схема сходится со скоростью и имеет р-ый порядок точности по hи q-ый порядок по τ.

Определим сеточную функцию погрешности δhкак разность между решением дифференциальной задачи, рассматриваемом в узлах сетки, и разностным решением: . При этом значение δhв узле с номером (i, j)определяется соотношением (2.9). Выразим uh, через Uhи δhи подставим в уравнение (2.8). Имеем

(2.10)

Величина Rhназывается невязкой (погрешностью аппроксимации) разностной схемы. Она равна разности между левой и правой частями (2.8) при подстановке в это уравнение решения дифференциальной задачи (2.7).

Введем некоторую характерную величину невязки R,например

Тогда при R = O(hk) аппроксимация имеет k-ый порядок относительно h. Если значения h и τ независимы, то при порядок аппроксимации разностной схемы р-ыйпо пространству и q—ыйпо времени.

Разностная схема (2.8) аппроксимирует исходную дифференциальную задачу (2.7), если при измельчении сетки невязка стремится к нулю, т.е.

Аппроксимация такого типа, т.е. когда невязка стремится к нулю при стремлении к нулю h и τ по любому закону без каких-либо условий, называется безусловной или абсолютной аппроксимацией. В случае условной аппроксимации накладываются некоторые условия на размеры шагов по пространству и времени. Например, если , то R→ 0 при и , т.е. разностная задача аппроксимирует исходную при условии, что τ стремится к нулю быстрее, чем h2. Так, при t = h2аппроксимация в данном примере отсутствует.

Разностная схема (2.8) называется устойчивой,если ее решение непрерывно зависит от входных данных, т.е. малому изменению входных данных соответствует малое изменение решения. Устойчивость характеризует чувствительность разностной схемы к различного рода погрешностям. Она является внутренним свойством разностной задачи, и это свойство не связывается непосредственно с исходной дифференциальной задачей (в отличие от сходимости и аппроксимации).

По аналогии с аппроксимацией устойчивость бывает условной и безусловной в зависимости от того, накладываются или нет ограничения на соотношения между шагами по разным переменным.

В теории разностных схем рассматриваются разные способы исследования аппроксимации исходной дифференциальной и разностной задач и проверки устойчивости разностных схем. Здесь мы лишь отметим, что эти исследования значительно проще, чем доказательство сходимости разностного решения к точному. Поэтому пользуются следующим утверждением.

Теорема. Если решение исходной дифференциальной задачи (2.7) существует, а разностная схема (2.8) устойчива и аппроксимирует задачу (2.7) на данном решении с порядком k, то разностное решение сходится к точному со скоростью O(h(k)).

Короче говоря, из аппроксимации и устойчивости следует сходимость. Поэтому, доказав аппроксимацию и устойчивость разностной схемы, можем быть уверены в ее сходимости.

Проиллюстрируем исследование разностных схем на примере рассмотренных выше двух схем для уравнения теплопроводности — явной схемы (2.3) и неявной схемы (2.4). Будем считать, что решение U(x,t) дифференциальной задачи (2.2) существует, а частные производные ¶2U/¶t2и ¶4U/¶x4 непрерывны и ограничены в расчетной области. Тогда в соответствии с формулами численного дифференцирования для каждого узла можно написать следующие соотношения:

;

. (2.11)

Найдем погрешность аппроксимации исходного уравнения (2.2) с помощью разностной схемы (2.3) для произвольного узла сетки :

Подставим в это равенство соотношения (2.11). При этом заметим, что поскольку U(x, t) является точным решением уравнения (2.2), то

(2.12)

Следовательно, максимальное значение невязки с учетом (2.11), (2.12) имеет порядок

Аналогичную оценку невязки можно получить и для разностной схемы (2.4).

Таким образом, разностные схемы (2.3) и (2.4) аппроксимируют исходное дифференциальное уравнение (2.2) со вторым порядком по h и с первым порядком по τ. Начальное и граничные условия задачи (2.2) аппроксимируются на границах точно, поскольку здесь значения сеточной функции равны значениям решения: Г – граница расчетной области (t= 0, х = 0, х = 1).

Исследуем теперь устойчивость данных разностных схем. Начнем с явной схемы (2.3) при граничных условиях (2.5) и начальном условии (2.6). Найдем из (2.3) значение сеточной функции на верхнем слое:

(2.13)

Допустим, что имеет место ограничение в виде неравенства

(2.14)

Тогда . Эти соотношения используем для оценки сеточного решения (2.13):

(2.15)

Введем теперь обозначение для наибольшего по модулю значения сеточной функции на j—омслое

и с учетом граничных условий (2.5) запишем неравенство (2.15) для значений решения на всем (j+ 1)-ом слое, включая границы:

. (2.16)

Отсюда при j= 0 получаем

(2.17)

Из (2.5), (2.6) следует, что

поэтому неравенство (2.17) можно записать в виде

(2.18)

При j= 1 из (2.16), (2.18) получаем

Аналогично, для некоторого j = Jимеем

(2.19)

Таким образом, значения сеточного решения на (J + 1)-ом слое не превосходят по модулю известных значений сеточного решения на нулевом слое (j= 0) и на границах i= 0, i = I[по (J+1)-ый слой включительно].

Неравенство (2.19) означает устойчивость разностной схемы (2.3). Покажем это. Разностная схема была выше названа устойчивой, если малому изменению входных данных соответствует малое изменение решения. Рассмотрим разностную задачу, входные данные которой, например начальное условие, подверглись малому изменению :

(2.20)

Решением этой задачи будет сеточная функция

(2.21)

где — решение исходной разностной задачи (2.3), (2.5), (2.6), а — некоторая поправка к решению. Подставим (2.21) в (2.20):

Отсюда с учетом (2.3), (2.5), (2.6) получаем разностную задачу относительно поправки

Эта задача совпадает с исходной, но при других начальных и граничных условиях. К ее решению применимо неравенство (2.19), которое в данном случае имеет вид и означает малость поправки к решению при малом изменении начального условия. Таким образом, схема (2.3) устойчива при выполнении условия (2.14). Можно показать, что при нарушении этого условия схема (2.3) будет неустойчивой, т.е. явная схема (2.3) условно устойчива. Из аппроксимации и устойчивости следует ее сходимость со скоростью O(h2+τ).

Исследуем теперь устойчивость неявной разностной схемы (2.4). Запишем, с помощью (2.4), (2.5) систему уравнений для нахождения неизвестных значений сеточной функции на верхнем слое:

(2.22)

Эта система может быть решена методом прогонки. Безусловная устойчивость неявной схемы (2.4) обеспечивается выполнением условий устойчивости метода прогонки для системы (2.22).

Устойчивость и сходимость разностных схем можно оценить путем расчетов с измельчением сетки . Однако это приводит к существенному увеличению объема вычислений и возрастанию суммарных погрешностей.

Многолетняя практика использования численных методов для решения инженерных задач на компьютерах показывает, что применение той или иной разностной схемы, даже если она исследована теоретически, требует ее тщательной апробации при решении конкретной задачи. Для этого проводятся методические вычислительные эксперименты, состоящие в расчетах с разными значениями шагов при разных исходных данных. Полезно также отладить методику с помощью тестовых задач, для которых либо удается получить аналитическое решение, либо имеется численное решение, найденное другим численным методом.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Устойчивость и сходимость разностных методов

Устойчивым методом называем метод, при использовании которого решение меняется мало при малых изменениях входных данных.

Соответственно, метод решения, при использовании которого малые возмущения входных данных, например, ошибки округления, приводят к сильному изменению результатов расчетов, назовем неустойчивым методом.

Численная устойчивость означает непрерывную зависимость решения от входных данных.

Будем рассматривать устойчивость методов на примере решения уравнения

, (9.21)

которое назовем тестовым уравнением. Решение уравнения (9.21) представляет собой затухающую экспоненту. Например, при начальном условии

(9.22)

точное решение равно . Будем считать метод решения уравнения (9.21) устойчивым, если он описывает затухающую экспоненту.

Пример 9.5. Решим задачу Коши для тестового уравнения (9.21), (9.22) методом Эйлера:

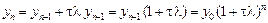
Решение Эйлера описывает экспоненциально затухающую функцию, если

. (9.23)

Если значение t выходит за пределы, указанные неравенствами (9.23), то не просто падает точность, а принципиально меняется характер решения. В то же время решение Эйлера устойчиво, если выполнены условии (9.23). Ранее уже говорилось, что ломаная Эйлера стремится к истинной интегральной кривой, если шаг приращения аргумента стремится к нулю. Заключаем отсюда, что метод Эйлера устойчив при выполнении ограничений на выбор шага приращения аргумента.

Метод Эйлера является одношаговым методом. Рассмотрим теперь примеры многошаговых методов.

Пример 9.6. Решим ту же задачу Коши (9.21), (9.22) двухшаговым методом третьего порядка:

. (9.24)

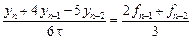
Подставим в формулу (9.24) и разрешим полученное выражение относительно . Решение в среде Mathcad приведено на рис. 9.4. Для решения двухшаговым методом дополнительно добавляем условие – значение точного решения в точке . Решение представлено в матрице М:

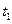
первый столбец дает значения аргумента;
второй – точное решение;
третий – приближенное решение.

Видим, что, начиная с некоторого шага, приближенное решение резко отличается от точного. Легко убедиться, что расхождение наблюдается и при уменьшении шага приращения аргумента. Заключаем, что метод является неустойчивым.

Пример 9.7.

Решим задачу Коши для тестового уравнения (9.21), (9.22) неявным двухшаговым методом третьего порядка:

. 9.25)

Подставив сюда и разрешив уравнение относительно , получим:

Решение в среде Mathcad приведено на рис. 9.5. Как и в предыдущем примере, решение представлено в матрице М:

первый столбец дает значения аргумента;
второй – точное решение;
третий – приближенное решение.

Видим, что приближенное решение совпадает с точным по меньшей мере в пределах трех значащих цифр. Легко убедиться, что характер приближенного решения остается тем же и при увеличении шага приращения аргумента. Заключаем, что данный метод является устойчивым.

Из рассмотренных примеров следует, что не все разностные методы пригодны для решения дифференциальных уравнений.

Для обнаружения неустойчивости метода

(9.26)

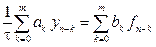
достаточно рассмотреть левую часть уравнения (9.26) , т.е. однородное разностное уравнение

. (9.27)

Ищем решение этого уравнения в виде

. (9.28)

Подставив это решение в уравнение (9.27) и сократив лишние сомножители, получим алгебраическое уравнение, которое называют характеристическим уравнением разностного метода:

. (9.29)

Очевидно, что если q – корень характеристического уравнения, то есть частное решение однородного разностного уравнения (9.27). Общее решение разностного уравнения представляет собой взвешенную сумму частных решений. Если все корни характеристического уравнения различны, то общее решение уравнения (9.27) равно сумме

, (9.30)

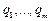
где A_k – постоянные, определяемые из начальных условий. Если среди корней характеристического уравнения есть кратный корень q_i кратности s, то линейно независимыми решениями разностного уравнения (9.27), соответствующими этому корню, являются функции:

. (9.31)

Собственные решения однородного уравнения (9.27) – это собственные решения разностного метода, существующие независимого от того, какое дифференциальное уравнение мы решаем. Характер собственных решений метода проявляется при решении дифференциального уравнения. Общее решение неоднородного ур-я

есть сумма какого-либо его частного решения и общего решения соответствующего однородного уравнения. Если среди собственных решений есть безгранично нарастающие, то метод вносит сильные искажения в решение дифференциального уравнения и оказывается фактически непригодным – оказывается неустойчивым.

Вернемся еще раз к примеру 9.6 – решение тестового уравнения

с помощью двухшагового метода:

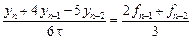
Характеристическое уравнение для однородного разностного уравнения

(9.32)

Решение характеристического уравнения:

Соответственно решение однородного уравнения (9.32) включает две компоненты: константу 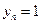и быстро растущую компоненту .

Однородное разностное уравнение всегда имеет тривиальное решение – это решение с нулевыми начальными условиями. Однако для неустойчивого метода даже незначительные возмущения нулевых начальных условий вызывают безграничный рост решения разностного уравнения. На рис. 9.6 показано решение уравнения (9.32) для случая малых начальных условий. Видим, что решение быстро растет.

Устойчивость решения разностного уравнения теорема о сходимости к точному решению

Наличие безгранично растущего собственного решения разностного метода искажает решение дифференциального уравнения и делает метод непригодным.

Найдем собственные решения для неявного разностного метода

Однородное уравнение имеет вид:

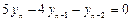
Решения характеристического уравнения равны: , и среди собственных решений разностного метода нет безгранично нарастающих.

Разностный метод удовлетворяет условию корней, если все корни характеристического уравнения 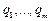лежат внутри или на границе единичного круга комплексной плоскости, причем на границе круга нет кратных корней.

Проверим, удовлетворяет ли условию корней метод Милна .

Характеристическое уравнение метода имеет вид:

Оба корня уравнения лежат на единичной окружности, но не являются кратными, следовательно, метод Милна удовлетворяет условию корней.

Выполнение условия корней не гарантирует, что метод сходится при любом значении шага приращения аргумента.

всегда является корнем характеристического уравнения

Это следует из уравнения для коэффициентов метода: .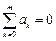

Замечании 3. Все методы Адамса 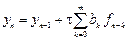удовлетворяют условию корней, т.к. характеристическое уравнение методов имеет всего один корень .

Для устойчивых методов порядок аппроксимации удовлетворяет неравенству

Для явных m-шаговых устойчивых методов порядок аппроксимации не превосходит m.

Вопросы для повторения

Формула линейного разностного m-шагового метода общего вида. Формула метода Адамса.
Достоинства и недостатки многошаговых методов. Достоинства и недостатки неявных методов.
Метод предиктор-корректор.
Порядок явного и неявного m-шагового метода общего вида. Порядок метода Адамса.
Характеристическое уравнение m-шагового метода.
Условие корней для линейного разностного m-шагового метода. Что гарантирует выполнение условия корней? Выполняется ли условие корней для методов Адамса?