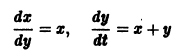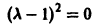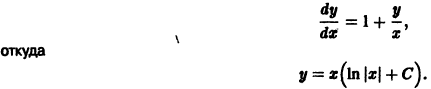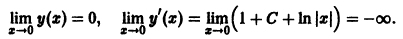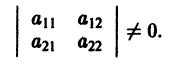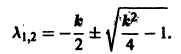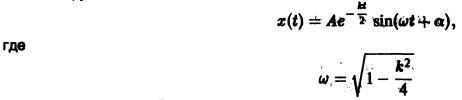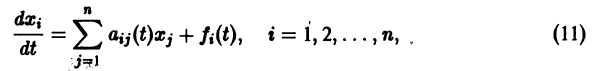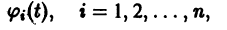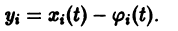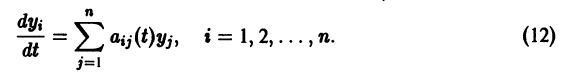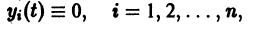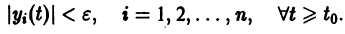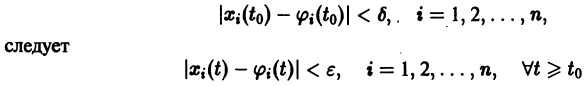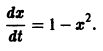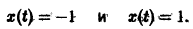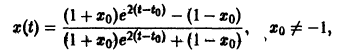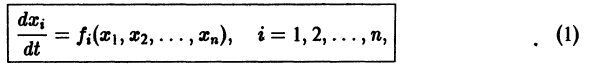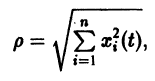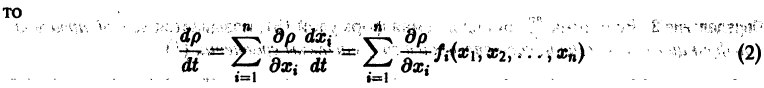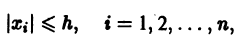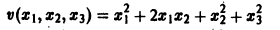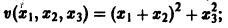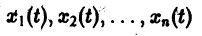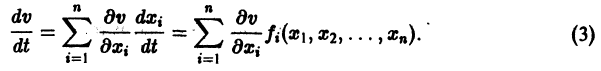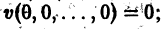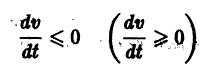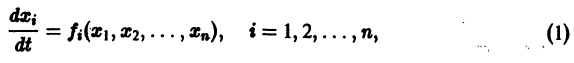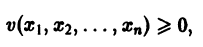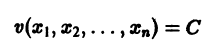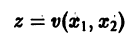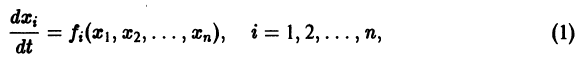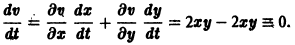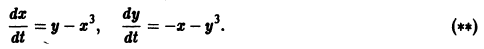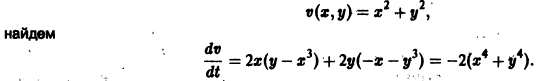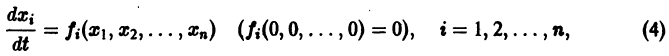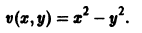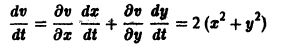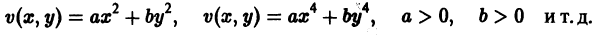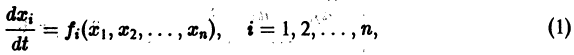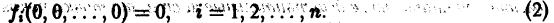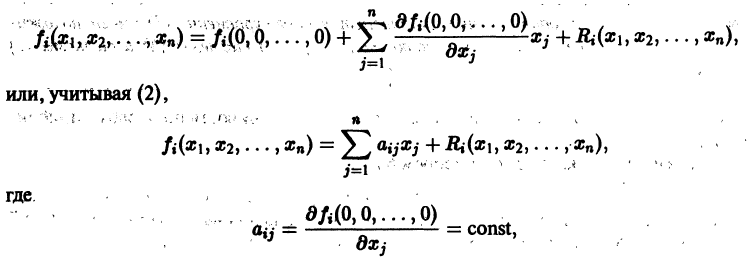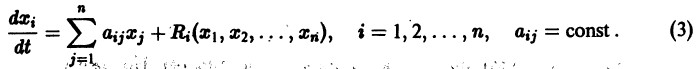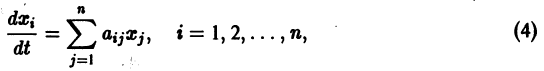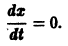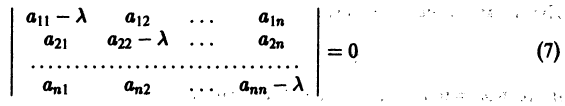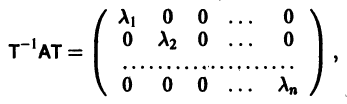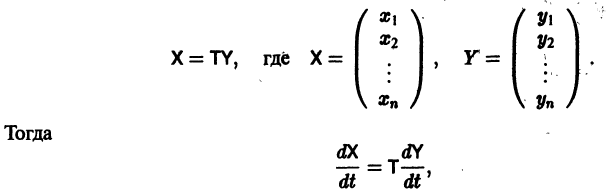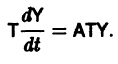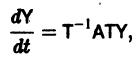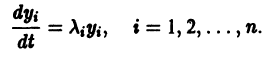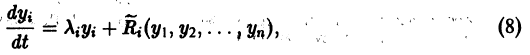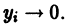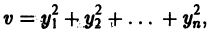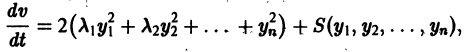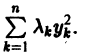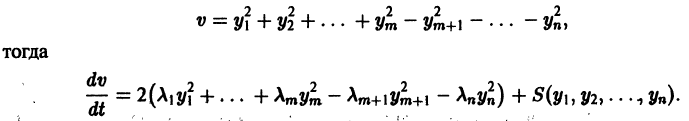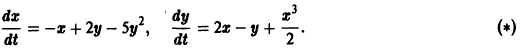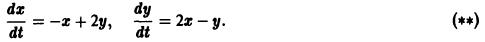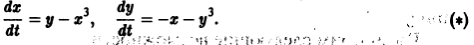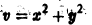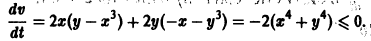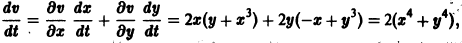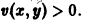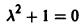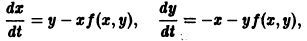Рассмотрим вопрос о зависимости решения задачи Коши от начальных данных. Пусть дана задача Коши
Если функция f(t, х) непрерывна по совокупности аргументов и имеет ограниченную производную 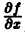

Справедлива следующая теорема о непрерывной зависимости решения от начальных условий.
Теорема:
Если правая часть f(t, х) дифференциального уравнения
непрерывна по совокупности переменных и имеет ограниченную частную производную 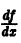
удовлетворяющее начальному условию 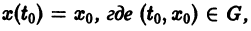
Иными словами, пусть через точку 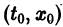
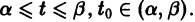
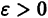
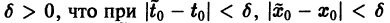
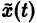
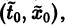
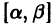
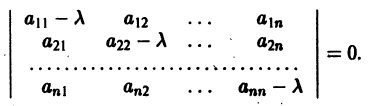
Аналогичная теорема справедлива и для системы дифференциальных уравнений
При выполнении условий теоремы (1) решение задачи Коши существует, единственно и непрерывно зависит от начальных данных. В этом случае говорят, что задача Коши поставлена корректно. Существенным является то обстоятельство, что отрезок [а, b] изменения t конечен. Однако во многих задачах нас интересует зависимость решения от начальных данных в бесконечном промежутке 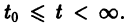
Остановимся вкратце на понятии о продолжаемости решения. Пусть имеем систему дифференциальных уравнений
где t — независимая переменная (время); 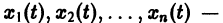
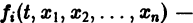
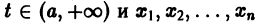
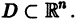
в их области определения непрерывны по совокупности аргументов и имеют ограниченные частные производные по 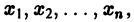
для каждой системы значений
существует единственное решение
системы (3), определенное в некотором интервале 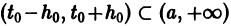
Введем следующее понятие. Пусть
— решение задачи Коши (3)-(4), определенное на некотором интервале I = (t1,t2). Это решение может бьггь продолжено, вообще говоря, на больший интервал времени. Решение
называется продолжением решения 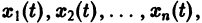
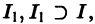
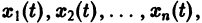
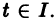
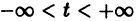
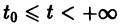
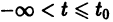
Для дальнейших рассмотрений важен вопрос о существовании решения хi(t), 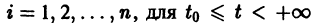
где 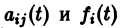
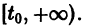
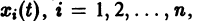
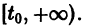
Не все системы обладают таким свойством. Например, для скалярного уравнения
непрерывна и имеет производные всех порядков по х. Нетрудно проверить, что функция
является решением задачи
Однако это решение существует только в интервале 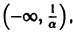
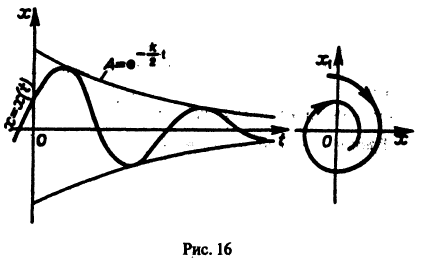
Уравнение (5) есть уравнение сверхбыстрого размножения, когда прирост пропорционален числу всевозможных пар. Его решение показывает, что при таком законе прироста населения количество населения становится бесконечным за конечное время (в то время как обычный закон прироста — экспоненциальный).
Задача:
Показать, что решения уравнения
нельзя продолжить неограниченно ни вправо, ни влево.
- Устойчивость по Ляпунову. Основные понятия и определения
- Устойчивость автономных систем. Простейшие типы точек покоя
- Простейшие типы точек покоя
- Метод функций Ляпунова
- Устойчивость по первому (линейному) приближению
- Устойчивость по Ляпунову: основные понятия и определения
- НАУЧНАЯ БИБЛИОТЕКА — РЕФЕРАТЫ — Устойчивость систем дифференциальных уравнений
- 💡 Видео
Видео:Устойчивость 1 ОпределениеСкачать

Устойчивость по Ляпунову. Основные понятия и определения
Рассмотрим дифференциальное уравнение первого порядка
где функция f(t,x) определена и непрерывна для 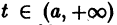
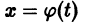
есть решение уравнения (1), удовлетворяющее начальному условию
Пусть, далее, функция
есть решение того же уравнения, удовлетворяющее другому начальному условию
Предполагается, что решения 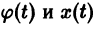
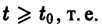
Определение:
Решение 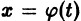
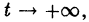
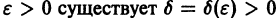
для всех 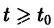
Это значит, что решения, близкие по начальным значениям к решению 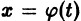
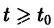
уравнения (1) устойчиво, если, какой бы узкой ни была е-полоска, содержащая кривую 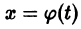
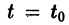
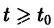
Если при сколь угодно малом 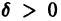
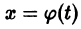
Определение:
Решение 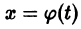
1) решение 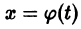
2) существует 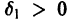
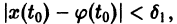
Это означает, что все решения х = x(t), близкие по начальным условиям к асимптотически устойчивому решению 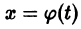
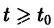
Вот простая физическая модель. Пусть шарик лежит на дне полусферической лунки (находится в положении равновесия). Если малым возмущением вывести шарик из этого положения, то он будет колебаться около него. При отсутствии трения положение равновесия будет устойчивым, при наличии трения колебания шарика будут уменьшаться с возрастанием времени, т. е. положение равновесия будет асимптотически устойчивым.
Пример:
Исследовать на устойчивость тривиальное решение
Решение 
Решение уравнения (*), удовлетворяющее начальному условию
Легко видеть (рис. 2), что, какова бы ни была 
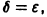
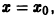
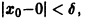
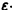
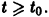
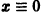
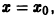
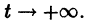
Пример:
Исследовать на устойчивость тривиальное решение 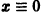
Решение уравнения (**), удовлетворяющее начальному условию
Возьмем любое 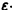
Поскольку 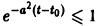
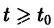
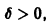
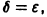
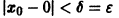
Согласно определению (1) это означает, что решение 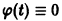
поэтому решение 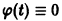
Пример:
Показать, что решение
В самом деле, при сколь угодно малом 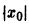
этого уравнения не удовлетворяет условию
при достаточно больших t > to. Более того, при любых 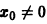
Рассмотрим теперь систему дифференциальных уравнений
где функции fi определены для 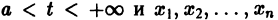
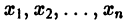
Определение:
системы (4) называется устойчивым по Ляпунову при 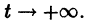
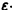
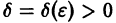
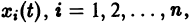
для всех 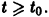
Если при сколь угодно малом 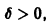
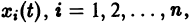
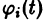
Определение:
системы (4) называется асимптотически устойчивым, если:
1) решение это устойчиво;
2) существует 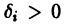
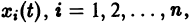
Пример:
Исходя из определения устойчивости по Ляпунову, показать, что решение системы
удовлетворяющее начальным условиям
устойчиво.
Решение системы (*), удовлетворяющее начальным условиям (**), есть
Решение этой системы, удовлетворяющее условиям 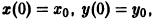
Возьмем произвольное 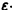
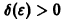
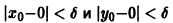
для всех 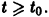
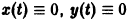
то при 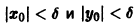
для всех 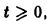
Из устойчивости нетривиального решения дифференциального уравнения не следует ограниченности этого решения. Рассмотрим, например, уравнение
Решением этого уравнения, удовлетворяющим условию х(0) = 0, является функция
Решение, удовлетворяющее начальному условию 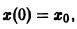
Геометрически очевидно (рис.5), что для всякого 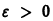
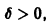
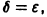
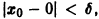
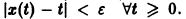
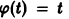
Из ограниченности решений дифференциального уравнения не следует устойчивости решений.
Рассмотрим уравнение
Оно имеет очевидные решения
Интегрируя уравнение (6), находим
Все решения (7) и (8) ограничены на 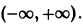
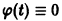
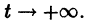
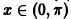
Таким образом, ограниченность и устойчивость решений являются понятиями, независимыми друг от друга.
Замечание:
Исследуемое на устойчивость решение
системы (4) всегда можно преобразовать в тривиальное решение
другой системы заменой
В самом деле, пусть имеем (для простоты) одно дифференциальное уравнение
и пусть требуется исследовать на устойчивость какое-либо решение 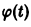
(величину 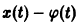
и подстановка в (*) приводит к равенству
Но 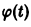
Обозначив здесь правую часть через F(t, у), получим
Это уравнение имеет решение 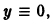
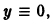
Таким образом, вопрос об устойчивости решения 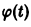
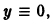
Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

Устойчивость автономных систем. Простейшие типы точек покоя
Нормальная система дифференциальных уравнений называется автономной, если ее правые части fi не зависят явно от t, т. е. если она имеет вид
Это значит, что закон изменения неизвестных функций, описываемый автономной системой, не меняется со временем, как это бывает с физическими законами. Пусть имеем автономную систему
и пусть (а1, a2, …, аn) — такая совокупность чисел, что
Тогда система функций
будет решением системы (1). Точку 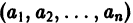
есть точка покоя этой системы. Обозначим через S(R) шар
и будем считать, что для рассматриваемой системы в шаре S(R) выполнены условия теоремы существования и единственности решения задачи Коши.
Определение:
Будем говорить, что точка покоя
системы (1) устойчива, если для любого 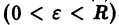
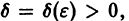
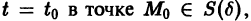
1) она устойчива;
2) существует такое 
Поясним это определение примерами.
Пример:
Траектории здесь — концентрические окружности
с центром в начале координат — единственной точкой покоя системы. Если взять 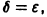
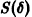
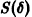
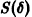
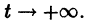
Пример:
Пусть дана система
поэтому траекториями являются лучи, входящие в начало координат (рис.8). Можно снова выбрать 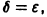
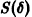
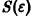
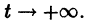
Пример:
Возьмем, наконец, систему
и траекториями являются лучи, исходящие из начала координат, но в отличие от примера 2 движение по лучам происходит в направлении от центра. Точка покоя неустойчива.
Видео:Устойчивость 5 Устойчивость по первому приближению Теорема ПримерыСкачать

Простейшие типы точек покоя
Исследуем расположение траекторий в окрестности точки покоя х = 0, у = 0 системы двух линейных однородных уравнений с постоянными коэффициентами:
Решение будем искать в виде
Для определения 
Величины 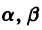
Возможны следующие случаи.
А. Корни 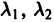
- Пусть
Точка покоя (0,0) в этом случае асимптотически устойчива, так как из-за наличия множителей
все точки каждой траектории, находившиеся в начальный момент
в произвольной
окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой,
окрестности начала координат, а при
стремятся к этому началу. Такая точка покоя называется устойчивым узлом
При С2 = 0 из (4) получаем
и траекториями являются два луча, входящие в начало координат с угловым коэффициентом
Аналогично, при С1 = 0 получаем еще два луча, входящие в начало координат с угловым коэффициентом
Пусть теперь 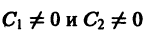
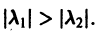
т. е. все траектории (исключая лучи 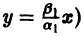
2. Если 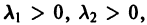
Пример:
Для нее точка О(0,0) — точка покоя. Характеристическое уравнение
имеет корни 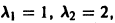
Оно имеет решения
так что траекториями системы будут лучи падающие с координатными полуосями, семейство парабол, касающихся оси Oх в начале координат (рис. 11)
3. Пусть теперь 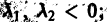
При С2 = 0 получаем решение
С возрастанием t точка этой траектории движется по лучу
в направлении от начала 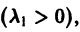
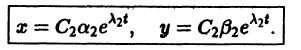
Отсюда видно, что при возрастании t точка движется по лучу
в направлении к началу координат 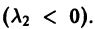
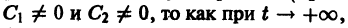
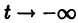
Пример:
Исследуем характер точки покоя О(0,0) системы
Характеристическое уравнение системы
имеет корни 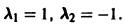
интегрируя которое получаем
Уравнение (6) имеет также решения
Таким образом, интегральные кривые этого уравнения (траектории системы (5)) — равнобочные гиперболы и лучи, совпадающие с координатными полуосями.
Б. Корни 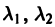
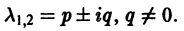
где C1 и C2 — произвольные постоянные, а 
- Пусть
в этом случае множитель
стремится к нулю при
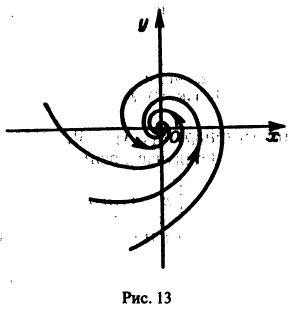
а вторые множители в (7) — ограниченные периодические функции. Траектории — спирали, асимптотически приближающиеся к началу координат при
Точка покоя х = 0, у = 0 асимптотически устойчива. Она называется устойчивым фокусом (рис. 13).,
- Если
то этот случай переходит в предыдущий при замене t на -t. Траектории не отличаются от траекторий предыдущего случая, но движение по ним при возрастании t происходит в противоположном направлении. Точка покоя неустойчива — неустойчивый фокус.
- Если же
то решения системы (2) — периодические функции. Траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром (рис. 14). Центр является устойчивой точкой покоя, однако асимптотической устойчивости нет, так как решение
не стремится к нулю при
Пример. Рассмотрим систему уравнений
Характеристическое уравнение системы
имеет комплексные корни
Перейдем от системы к одному уравнению
и введем полярные координаты 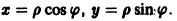
Используя уравнение (9), находим, что
Эти интегральные кривые являются логарифмическими спиралями, навивающимися на начало координат, которое достигается в пределе при 
Интегральные кривые этого уравнения — окружности с центром в начале координат, которое при а = 0 является точкой покоя системы (8) типа центра.
В. Корни 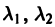
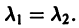
( 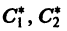
- Если
то из-за наличия множителя
решения х(t), y(t) стремятся к нулю при
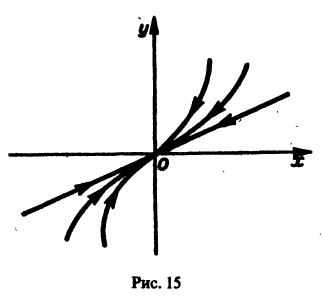
Точка покоя х = 0, у = 0 асимптотически устойчива. Ее называют устойчивым вырожденным узлам (рис. 15). Он отличается от узла в случае А. 1 (там одна из траекторий имела касательную, отличную от всех остальных). Возможен также дикритический узел (см. рис. 8).
- При
замена t на -t приводит к предыдущему случаю, но движение по траекториям происходит в противоположном направлении. Точка покоя в этом случае называется неустойчивым вырожденным узлом.
Пример:
Для системы уравнений
имеет кратные корни 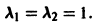
Поэтому все интегральные кривые проходят через начало координат, и все они имеют там ось Оу общей касательной.
Мы перебрали и исчерпали все возможности, поскольку случай 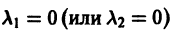
Пример:
Исследовать уравнение малых колебаний маятника с учетом трения.
Уравнение малых колебаний маятника в этом случае имеет вид
где x — угол малого отклонения маятника от вертикали, к — коэффициент трения. Заменим уравнение (*) эквивалентной системой
Характеристическое уравнение для системы (**)
Если 0
— частота колебаний, а величины А, а определяются из начальных условий.
График решения и фазовая кривая при 0
Сформулируем результаты, касающиеся устойчивости решений системы п линейных однородных дифференциальных уравнений первого порядка с постоянными коэффициентами
Рассмотрим для системы (10) характеристическое уравнение
Справедливы следующие предложения:
1) если все корни характеристического уравнения имеют отрицательную действительную часть, то все решения системы (10) асимптотически устойчивы. Действительно, в этом случае все слагаемые общего решения содержат множители 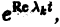
2) если хотя бы один корень 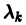
3) если характеристическое уравнение имеет простые корни с нулевой действительной частью (т. е. чисто мнимые или равные нулю корни), а остальные корни, если они есть, имеют отрицательную действительную часть, та все решения устойчивы, но асимптотической устойчивости нет.
Эти результаты относятся и к одному линейному дифференциальному уравнению с постоянными коэффициентами.
Следует обратить внимание на то, что для линейной системы все решения либо устойчивы, либо неустойчивы одновременна
Теорема:
Решения Системы линейных дифференциальных уравнений
либо все одновременно устойчивы, либо неустойчивы.
Преобразуем произвольное частное решение
системы (11) в тривиальное с помощью замены
Система (11) преобразуется при этом в линейную однородную систему относительно yi(t):
Следовательно, все частные решения системы (11) в смысле устойчивости ведут себя одинаково, а именно как тривиальное решение однородной системы (12).
В самом деле, пусть тривиальное решение
системы (12) устойчиво. Это значит, что для любого 
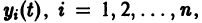
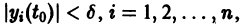
Замечая, что 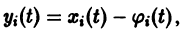
для всякого решения 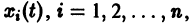
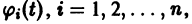
Это предложение не имеет места для нелинейных систем, некоторые решения которых могут быть устойчивыми, а другие — неустойчивыми.
Пример:
Рассмотрим нелинейное уравнение
Оно имеет очевидные решения
Решение x(t) = -1 неустойчиво, а решение x(t) = 1 является асимптотически устойчивым. В самом деле, при 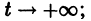
стремятся к +1. Это означает, согласно определению, что решение x(t) = 1 асимптотически устойчиво.
Замечание:
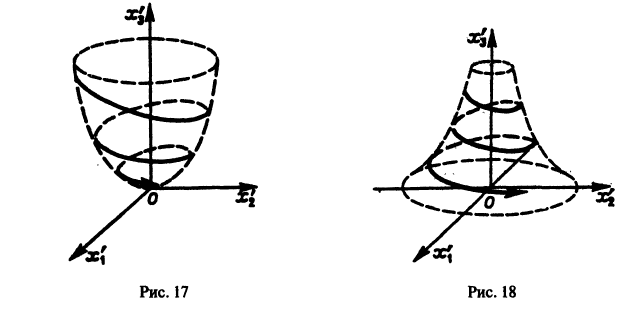
Как и в случае n = 2, можно исследовать расположение траекторий в окрестности точки покоя О(0,0,0) системы (10). Для n = 3 возможны так называемые узлофокусы (рис. 17), седлофокусы (рис. 18) и т. д.
Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Метод функций Ляпунова
Метод функций Ляпунова состоит в исследовании устойчивости точки покоя системы дифференциальных уравнений с помощью подходящим образом выбранной функции 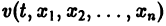
Ограничимся рассмотрением автономных систем
для которых Xi = 0, i = 1, 2,…, n, есть точка покоя.
Идея метода состоит в следующем. Предположим, что на устойчивость исследуется точка покоя 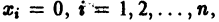
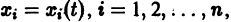
(производная вдоль траектории): Правая часть в (2) есть известная функция от х1, х2,…, хn, и можно исследовать ее знак. Если окажется, что 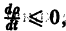
Определение:
Функция v(x1, х2, … xn), определенная в некоторой окрестности начала координат, называется знакоопределенной (знакоположительной или знакоотрицательной), если в области G
где h — достаточно малое положительное число, она может принимать значения только одного определенного знака и обращается в нуль лишь при
Так, в случае n = 3 функции
будут знакоположительными, причем здесь величина h > 0 может быть взята сколь угодно большой.
Определение:
Функция 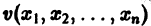
будет знакопостоянной (положительной). В самом деле, функцию v(x1, x2, x3) можно представить так:
отсюда видно, что она неотрицательна всюду, но обращается в нуль и при 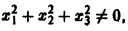
Пусть 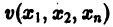
являются некоторыми функциями времени, удовлетворяющими системе дифференциальных уравнений (1). Тогда для полной производной функции v повремени имеем
Определение:
Величина 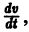
Определение:
Функций 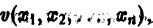
1) 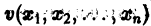
2) 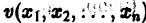
3) полная производная 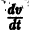
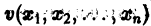
всюду в 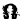
Теорема:
Теорема Ляпунова об устойчивости. Если для системы дифференциальных уравнений
существует дифференцируемая знакоопределенная функция 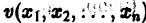
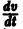
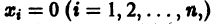
Приведем идею доказательства. Пусть для определенности 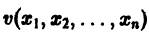
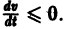
причем v = 0 лишь при 
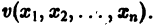
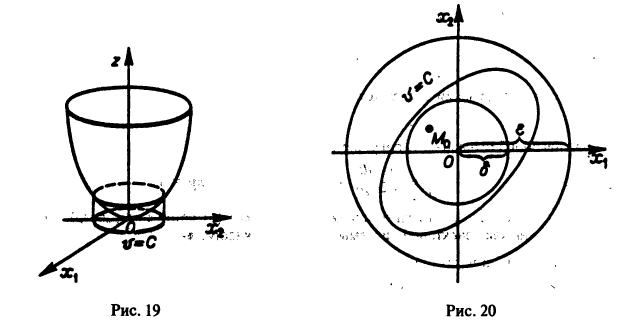
функции v являются, Как можно показать, замкнутыми поверхностями, внутри которых находится начало координат. Чтобы картина стала нагляднее, остановимся на случае n = 2. Так как 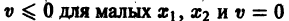
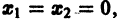
в общих чертах напоминает параболоид, вогнутый Вверх (рис. 19).
Линии уровня 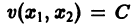
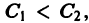
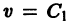
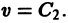
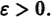
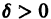
существует дифференцируемая знакоопределенная функция 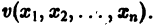
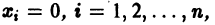
Пример:
Исследовать на устойчивость точку покоя О(0,0) системы
Выберем в качестве функции v(x, y) функцию
Эта функция знакоположительная. В силу системы (*) найдем
Из теоремы 3 следует, что точка покоя О(0,0) системы (*) устойчива (центр). Асимптотической устойчивости нет, так как траектория системы (*) — окружности.
Пример 2. Исследовать на устойчивость точку покоя О(0,0) системы
Таким образом, 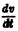
Теорема:
О неустойчивости. Пусть для системы дифференциальных уравнений
существует дифференцируемая в окрестности начала координат функция 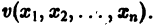
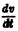
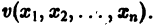
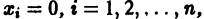
Пример:
Исследовать на устойчивость точку покоя О(0,0) системы
Для нее функция
знакоположительная. Так как сколь угодно близко к началу координат найдутся точки, в которых v > 0 (например, 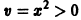
Метод функций Ляпунова оказывается универсальным и эффективным для широкого круга проблем теории устойчивости. Недостаток же метода в том, что достаточно общего конструктивного способа построения функций Ляпунова пока нет. В простейших случаях функцию Ляпунова можно искать в виде
Видео:Занятие "Вторичноротые – всё не то, чем кажется" // Неурочные беспозвоночные // Вадим МарьинскийСкачать

Устойчивость по первому (линейному) приближению
Пусть имеем систему дифференциальных уравнений
и пусть 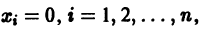
Будем предполагать, что функции 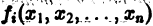
а слагаемые Ri содержат члены не ниже второго порядка малости относительно 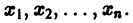
Так как понятие устойчивости точки покоя O(0,0,…, 0) связано с малой окрестностью начала координа’т в- фазовом пространстве, то естественно ожидать, что поведение решения (1) будет определяться главными линейными членами разложения функций fi по х. Поэтому наряду с системой (3) рассмотрим систему
называемую системой уравнений первого (линейного) приближения для системы (3).
Вообще говоря, строгой связи между системами (3) и (4) нет. Рассмотрим, например, уравнение
Здесь f(x) = 0; линеаризированное уравнение для уравнения (5) имеет вид
Решение 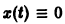
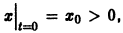
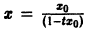
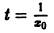
Теорема:
Если все корни характеристического уравнения
имеют отрицательные действительные части, то точка покоя 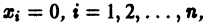
При выполнении условий теоремы возможно исследование на устойчивость по первому приближению.
Теорема:
Если хотя бы один корень характеристического уравнения (7) имеет положительную действительную часть, то точка покоя Xi= 0 системы (4) и системы (3) неустойчива.
В этом случае также возможно исследование на устойчивость по первому приближению.
Наметим идею доказательства теорем 6 и 7.
Пусть для простоты корни 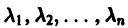
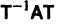
где 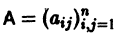
и система (4) преобразуется к виду
или, в силу выбора матрицы Т,
Система (3) при том же преобразовании перейдет в систему
причем в 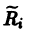
Рассмотрим следующие возможности:
1. Все корни 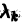
тогда производная 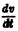
где 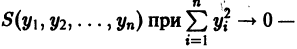
Таким образом, в достаточно малой окрестности 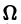
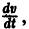
2. Некоторые из корней 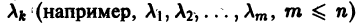
Отсюда видно, что сколь угодно близко к началу координат найдутся точки (например, такие, у которых 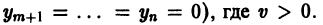
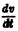
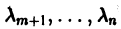
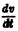
В критическом случае, когда все действительные части корней характеристического уравнения неположительны, причем действительная часть хотя бы одного корня равна нулю, на устойчивость тривиального решения системы (3) начинают влиять нелинейные члены Ri и исследование на устойчивость по первому приближению становится невозможным.
Пример:
Исследовать на устойчивость по первому приближению точку покоя х = 0, у = 0 системы
Система первого приближения имеет вид
Нелинейные члены удовлетворяют нужным условиям: их порядок не меньше 2. Составляем характеристическое уравнение для системы (**):
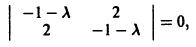
Корни характеристического уравнения 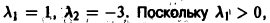
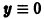
Пример:
Исследуем на устойчивость точку покоя О(0, 0) системы
Точка покоя х = 0, у = 0 системы (*) асимптотически устойчива, так как для этой системы функция Ляпунова
удовлетворяет условиям теоремы Ляпунова об асимптотической устойчивости. В частности,
В то же время точка покоя х = 0, у = 0 системы
В самом деле, для функции 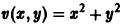
т.е. 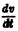
В силу теоремы 5 заключаем о неустойчивости точки покоя О(0,0) системы (**).
Для системы (*) и (**) система первого приближения одна и та же:
для системы (***) имеет чисто мнимые корни — критический случай (действительные части корней характеристического уравнения равны нулю). Для системы первого приближения (***) начало координат является устойчивой точкой покоя — центром. Системы (*) и (**) получаются малым возмущением правых частей (***) в окрестности начала координат. Однако эти малые возмущения приводят к тому, что для системы (*) точка покоя О(0,0) становится асимптотически устойчивой, а для системы (**) неустойчивой.
Этот пример показывает, что в критическом случае нелинейные члены могут влиять на устойчивость точки покоя.
Задача. Исследовать на устойчивость точку покоя О(0,0) системы
где функция f(х,у) разлагается в сходящийся отеленной ряд и f(0,0) = 0.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Филиппов №881(г) — Исследование решения на устойчивостьСкачать

Устойчивость по Ляпунову: основные понятия и определения
Пусть имеем систему дифференциальных уравнений
Решение , системы (1), удовлетворяющее начальным условиям , называется устойчивым no Ляпунову при , если для любого 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAAQBAMAAACb51DZAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/QHAQSFZiDGh0BCgsXHgm/CxLgAAALNJREFUGNNjYCAecHtgF8+vWYFNmEWCoX4DnOcOZ/IuYAhMANJMCiAem00AVFzRgEHxAlDAULYBJKsCk3C8wKD4iYFhborzA4i5xg4Q8QIGRSEGjglwK1gnOyGJm5VvQEgkwMVZPy8OgIufT4CaL8TA3IAw5zDYnI0GICe1w4VVDkPs1QK6/wFD1yalPIhzLKE61UQZHgYwsEsZgl3EZgmzhqn+uRiQCsuAhAPcdibVZxsYAOHLKP4AljeRAAAAAElFTkSuQmCC» /> существует 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAEYAAAAWCAMAAABKfhpBAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAQjHgIRHRwaZc8IGRQXGCR+L2IgAAAVVJREFUOMutVNuWwyAINN4Ab+H/v3YjamPitj3bbp4slYGZAZX6x8/qfkh5ioL+G8oOgbEeYprDGtz73Pyo5UA5rADZXPMKvAPRBtEMoNCzgW63wvZGjFCUomDbLy+M1MZ3Eulsx6JdYRJLsS4FsbSBC4cZOAMuknsvJEzThlho+TgKezZydjzTzAg3kiyFgZtMMYlRXLpsacvRN3HiVQu8yjdgXJPJ8ZFludWaRYB0FxX9CZQHzJGIlRmEKkSHoRLHVVgtd/sDyJ0wllO/PmB274dKv8LEs5+T1CYqGtFGYAjnfcAXIEdac+qgojlXWexD4st8mPhcmXpXPBJ/KgFZhW44UtuP1jVdfboZruv/uTaitEdAd86sNgF80H387DR+sK4GmVJCL+Xc8K8dctl6JPnXy3CEiZb4upr0yeu1mVvL8NkrWC5Da4398DVF+uIR/f77AQOYCjg2wpU7AAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> такое, что для всякого решения , системы (1), начальные значения которого удовлетворяют условиям
имеют место неравенства
Если при сколь угодно малом 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAARCAMAAACVS259AAAANlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADAR2LVAAAAEnRSTlMA5dARAV6h/4HAIUExsUAQcZHkvQX+AAAAz0lEQVQoz51S0RLDIAgThyJFV/v/Pztx7Wm1W2/zgTshJgEx5o/zeD5+QDu2ZJcbwlZnNDmt39ABQuIDwe5OHorZVFjrydCsu3whA74EIXnfFkodkw1j35FCjduhRZ0ddNaf+3YVjsR6WTkJQV9G4dODcMDVPJdHiYY5SuGY4LYqRU3I2J54jhfsDKiJ6VuXBu+8I+mQNhi5mZueVLgoEiHs4XOruM9dxxdKAwK9l2mQZQdK3atrsya72Xj6pmnb0NvsYQdh7KnD5S7HLMr9Ah4fBg4hVyWJAAAAAElFTkSuQmCC» /> хотя бы для одного решения , неравенства (3) не выполняются, то решение называется неустойчивым .
Если, кроме выполнения неравенств (3) при условии (2) выполняется также условие
то решение , называется асимптотически устойчивым .
Исследование на устойчивость решения , системы (1) можно свести к исследованию на устойчивость нулевого (тривиального) решения , некоторой системы, аналогичной системе (1),
Говорят, что точка , есть точка покоя системы (1′).
Применительно к точке покоя определения устойчивости и неустойчивости могут быть сформулированы так. Точка покоя , устойчива по Ляпунову , если, каково бы ни было 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAAQBAMAAACb51DZAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/QHAQSFZiDGh0BCgsXHgm/CxLgAAALNJREFUGNNjYCAecHtgF8+vWYFNmEWCoX4DnOcOZ/IuYAhMANJMCiAem00AVFzRgEHxAlDAULYBJKsCk3C8wKD4iYFhborzA4i5xg4Q8QIGRSEGjglwK1gnOyGJm5VvQEgkwMVZPy8OgIufT4CaL8TA3IAw5zDYnI0GICe1w4VVDkPs1QK6/wFD1yalPIhzLKE61UQZHgYwsEsZgl3EZgmzhqn+uRiQCsuAhAPcdibVZxsYAOHLKP4AljeRAAAAAElFTkSuQmCC» />, можно найти такое 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAARCAMAAACVS259AAAANlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADAR2LVAAAAEnRSTlMA5dARAV6h/4HAIUExsUAQcZHkvQX+AAAAz0lEQVQoz51S0RLDIAgThyJFV/v/Pztx7Wm1W2/zgTshJgEx5o/zeD5+QDu2ZJcbwlZnNDmt39ABQuIDwe5OHorZVFjrydCsu3whA74EIXnfFkodkw1j35FCjduhRZ0ddNaf+3YVjsR6WTkJQV9G4dODcMDVPJdHiYY5SuGY4LYqRU3I2J54jhfsDKiJ6VuXBu+8I+mQNhi5mZueVLgoEiHs4XOruM9dxxdKAwK9l2mQZQdK3atrsya72Xj6pmnb0NvsYQdh7KnD5S7HLMr9Ah4fBg4hVyWJAAAAAElFTkSuQmCC» />, что для любого решения , начальные данные которого , удовлетворят условию
Для случая геометрически это означает следующее. Каким бы малым ни был радиус цилиндра с осью , в плоскости найдется δ-окрестность точки такая, что все интегральные кривые , выходящие из этой окрестности, для всех будут оставаться внутри этого цилиндра (рис. 30).
Если кроме выполнения неравенств (3), выполняется также условие , то устойчивость асимптотическая .
Точка покоя , неустойчива , если при сколь угодно малом 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAARCAMAAACVS259AAAANlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADAR2LVAAAAEnRSTlMA5dARAV6h/4HAIUExsUAQcZHkvQX+AAAAz0lEQVQoz51S0RLDIAgThyJFV/v/Pztx7Wm1W2/zgTshJgEx5o/zeD5+QDu2ZJcbwlZnNDmt39ABQuIDwe5OHorZVFjrydCsu3whA74EIXnfFkodkw1j35FCjduhRZ0ddNaf+3YVjsR6WTkJQV9G4dODcMDVPJdHiYY5SuGY4LYqRU3I2J54jhfsDKiJ6VuXBu+8I+mQNhi5mZueVLgoEiHs4XOruM9dxxdKAwK9l2mQZQdK3atrsya72Xj6pmnb0NvsYQdh7KnD5S7HLMr9Ah4fBg4hVyWJAAAAAElFTkSuQmCC» /> хотя бы для одного решения , условие (3′) не выполняется.
Пример 1. Исходя из определения устойчивости по Ляпунову, исследовать на устойчивость решение уравнения, удовлетворяющее начальному условию
Решение. Уравнение (5) есть линейное неоднородное уравнение. Его общее решение . Начальному условию удовлетворяет решение
уравнения (5). Начальному условию удовлетворяет решение
Рассмотрим разность решений (7) и (6) уравнения (5) и запишем ее так:
Отсюда видно, что для всякого 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAAQBAMAAACb51DZAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/QHAQSFZiDGh0BCgsXHgm/CxLgAAALNJREFUGNNjYCAecHtgF8+vWYFNmEWCoX4DnOcOZ/IuYAhMANJMCiAem00AVFzRgEHxAlDAULYBJKsCk3C8wKD4iYFhborzA4i5xg4Q8QIGRSEGjglwK1gnOyGJm5VvQEgkwMVZPy8OgIufT4CaL8TA3IAw5zDYnI0GICe1w4VVDkPs1QK6/wFD1yalPIhzLKE61UQZHgYwsEsZgl3EZgmzhqn+uRiQCsuAhAPcdibVZxsYAOHLKP4AljeRAAAAAElFTkSuQmCC» /> существует 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAARCAMAAACVS259AAAANlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADAR2LVAAAAEnRSTlMA5dARAV6h/4HAIUExsUAQcZHkvQX+AAAAz0lEQVQoz51S0RLDIAgThyJFV/v/Pztx7Wm1W2/zgTshJgEx5o/zeD5+QDu2ZJcbwlZnNDmt39ABQuIDwe5OHorZVFjrydCsu3whA74EIXnfFkodkw1j35FCjduhRZ0ddNaf+3YVjsR6WTkJQV9G4dODcMDVPJdHiYY5SuGY4LYqRU3I2J54jhfsDKiJ6VuXBu+8I+mQNhi5mZueVLgoEiHs4XOruM9dxxdKAwK9l2mQZQdK3atrsya72Xj6pmnb0NvsYQdh7KnD5S7HLMr9Ah4fBg4hVyWJAAAAAElFTkSuQmCC» /> (например, ) такое, что для всякого решения уравнения (5), начальные значения которого удовлетворяют условию , выполняется неравенство
для всех . Следовательно, решение является устойчивым. Более того, поскольку
решение является асимптотически устойчивым.
Это решение является неограниченным при .
Приведенный пример показывает, что из устойчивости решения дифференциального уравнения не следует ограниченности решения.
Пример 2. Исследовать на устойчивость решение уравнения
Решение. Оно имеет очевидные решения
Интегрируем уравнение (8): , или , откуда
Все решения (9) и (10) ограничены на . Однако решение неустойчиво при , так как при любом имеем (рис.31).
Следовательно, из ограниченности решений дифференциального уравнения , вообще говоря, не следует их устойчивости . Это явление характерно для нелинейных уравнений и систем.
Пример 3. Исходя из определения устойчивости по Ляпунову, показать, что решение системы, удовлетворяющее начальным условиям , устойчиво
Решение. Решение системы (11), удовлетворяющее заданным начальным условиям, есть . Любое решение этой системы, удовлетворяющее условиям , имеет вид
Возьмем произвольное 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAAQBAMAAACb51DZAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/QHAQSFZiDGh0BCgsXHgm/CxLgAAALNJREFUGNNjYCAecHtgF8+vWYFNmEWCoX4DnOcOZ/IuYAhMANJMCiAem00AVFzRgEHxAlDAULYBJKsCk3C8wKD4iYFhborzA4i5xg4Q8QIGRSEGjglwK1gnOyGJm5VvQEgkwMVZPy8OgIufT4CaL8TA3IAw5zDYnI0GICe1w4VVDkPs1QK6/wFD1yalPIhzLKE61UQZHgYwsEsZgl3EZgmzhqn+uRiQCsuAhAPcdibVZxsYAOHLKP4AljeRAAAAAElFTkSuQmCC» /> и покажем, что существует 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAEYAAAAWCAMAAABKfhpBAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAQjHgIRHRwaZc8IGRQXGCR+L2IgAAAVVJREFUOMutVNuWwyAINN4Ab+H/v3YjamPitj3bbp4slYGZAZX6x8/qfkh5ioL+G8oOgbEeYprDGtz73Pyo5UA5rADZXPMKvAPRBtEMoNCzgW63wvZGjFCUomDbLy+M1MZ3Eulsx6JdYRJLsS4FsbSBC4cZOAMuknsvJEzThlho+TgKezZydjzTzAg3kiyFgZtMMYlRXLpsacvRN3HiVQu8yjdgXJPJ8ZFludWaRYB0FxX9CZQHzJGIlRmEKkSHoRLHVVgtd/sDyJ0wllO/PmB274dKv8LEs5+T1CYqGtFGYAjnfcAXIEdac+qgojlXWexD4st8mPhcmXpXPBJ/KgFZhW44UtuP1jVdfboZruv/uTaitEdAd86sNgF80H387DR+sK4GmVJCL+Xc8K8dctl6JPnXy3CEiZb4upr0yeu1mVvL8NkrWC5Da4398DVF+uIR/f77AQOYCjg2wpU7AAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> такое, что при имеют место неравенства
Это и будет означать, согласно определению, что нулевое решение системы (11) устойчиво по Ляпунову. Имеем, очевидно,
для всех . Поэтому, если то и подавно
Следовательно, если, например, взять , то при и в силу (12) будут иметь место неравенства (13) для всех , т.е. действительно нулевое решение системы (11) устойчиво по Ляпунову , но эта устойчивость не асимптотическая.
Теорема. Решения системы линейных дифференциальных уравнений
либо все одновременно устойчивы, либо неустойчивы.
Это предложение не верно для нелинейных систем, некоторые решения которых могут быть устойчивыми, а другие — неустойчивыми.
Пример 4. Исследовать на устойчивость решение нелинейного уравнения
Решение. Оно имеет очевидные решения и .
Решение этого уравнения неустойчиво, а решение является асимптотически устойчивым. В самом деле, при все решения уравнения (14)
Видео:Дифференциальные уравнения 7. Устойчивость по Ляпунову. Асимптотическая устойчивостьСкачать

НАУЧНАЯ БИБЛИОТЕКА — РЕФЕРАТЫ — Устойчивость систем дифференциальных уравнений
Министерство образования РФ
«Специальные разделы математики»
Тема: «Устойчивость систем дифференциальных уравнений»
Студент: Новичков А. А.
Преподаватель: Панова Е. В.
1. Свойства систем дифференциальных уравнений. 4
1.1. Основные определения. 4
1.2. Траектории автономных систем. 5
1.3. Предельные множества траекторий. 6
1.4. Траектории линейных систем на плоскости. 8
1.5. Линейные однородные системы с периодическими коэффициентами. 10
2. Устойчивость решений систем дифференциальных уравнений. 12
2.1. Устойчивость по Ляпунову. 12
2.2. Устойчивость линейных однородных систем. 14
2.3. Устойчивость периодических решений. 17
2.4. Классификация положений равновесия системы второго порядка. 18
2.5. Автономные системы на плоскости. Предельные циклы. 23
2.6. Устойчивость по первому приближению. 25
2.7. Экспоненциальная устойчивость. 28
3. Второй метод Ляпунова. 29
3.1. Основные определения. 29
3.2. Теоремы второго метода Ляпунова. 30
3.3. Устойчивость по первому приближению. 33
Список литературы. 37
Решения большинства дифференциальных уравнений и их систем не
выражаются через элементарные функции, и в этих случаях при решении
конкретных уравнений применяются приближенные методы интегрирования. Вместе
тем часто бывает необходимо знать не конкретные численные решения, а
особенности решений: поведение отдельных решений при изменении параметров
систем, взаимное поведение решений при различных начальных данных, является
ли решение периодическим, как меняется общее поведение системы при
изменении параметров. Все эти вопросы изучает качественная теория
Одним из основных вопросов этой теории является вопрос об устойчивости
решения, или движения системы, если ее трактовать как модель физической
системы. Здесь важнейшим является выяснение взаимного поведения отдельных
решений, незначительно отличающихся начальными условиями, то есть будут ли
малые изменения начальных условий вызывать малые же изменения решений. Этот
вопрос был подробно исследован А. М. Ляпуновым.
Основу теории Ляпунова составляет выяснение поведения решений при
асимптотическом стремлении расстояния между решениями к нулю. В данной
курсовой работе излагаются основы теории Ляпунова устойчивости непрерывных
гладких решений систем дифференциальных уравнений первого порядка, а
именно: в главе 1 излагаются основные определения, необходимые для изучения
устойчивости; в главе 2 дается понятие устойчивости решений систем в общем
виде и по первому приближению; в главе 3 излагаются основы второго метода
1. Свойства систем
1.1. Основные определения.
Пусть [pic] — непрерывные в области G (n+1)-мерного пространства
Определение. Совокупность уравнений
называется нормальной системой n дифференциальных уравнений первого
порядка. Ее можно записать в матричной форме, если положить
Определение. Решением системы (1) на интервале (a, b) называется
совокупность n функций [pic], непрерывно дифференцируемых на этом
интервале, если при всех [pic]:
Задача Коши для системы (1) ставится следующим образом: найти решение
[pic] системы, определенное в окрестности точки [pic], которое
удовлетворяет начальным условиям [pic] …, [pic], где [pic] — заданная точка
из области G. Решение задачи Коши существует и единственно, если все
функции в правых частях уравнений системы (1) непрерывно дифференцируемы по
всем [pic] в окрестности точки [pic].
Каждому решению системы (1) сопоставляется 2 геометрических объекта:
интегральная кривая и траектория.
Определение. Если [pic] — решение системы (1) на промежутке (a, b), то
множество точек (x, [pic]), [pic], (n+1)-мерного пространства называется
интегральной кривой решения, а множество точек ([pic]), [pic], n-мерного
пространства называется траекторией решения. Заметим, что из существования
и единственности решения задачи Коши интегральные кривые не могут
пересекаться или иметь общих точек, однако траектории могут пересекаться
без нарушения единственности, так как начальная точка определяется n+1
координатой. В частности траектория может совпадать с точкой (положение
Система (1) называется автономной, если в правые части уравнений не
входит явно независимая переменная. Система (1) называется линейной, если
или в матричной форме [pic] (1′)
где [pic] [pic], [pic].
Фундаментальной матрицей линейной однородной системы называется
матричная функция ?(t), определитель которой отличен от нуля и столбцы
которой являются решениями системы: [pic]. С помощью фундаментальной
матрицы ?(t) общее решение системы можно записать в виде [pic].
Фундаментальная матрица, обладающая свойством [pic], называется
нормированной при [pic]. Если [pic] — нормированная при [pic]
фундаментальная матрица, то частное решение системы записывается в виде
[pic], где [pic] — начальное при [pic] значение решения.
1.2. Траектории автономных систем.
Будем рассматривать автономную систему в векторной форме:[pic] (2)
где функция f(x) определена в [pic].
Автономные системы обладают тем свойством, что если [pic] — решение
уравнения (2), то [pic], [pic], также решение уравнения (2). Отсюда в
частности следует, что решение [pic] можно записать в виде [pic]. В
геометрической интерпретации эта запись означает, что если две траектории
уравнения (2) имеют общую точку, то они совпадают. При этом можно заметить,
что траектория вполне определяется начальной точкой [pic], поэтому можно
везде считать [pic].
Пусть [pic] — положение равновесия, т. е. [pic]. Для того чтобы точка
[pic] была положением равновесия, необходимо и достаточно, чтобы [pic].
Предположим теперь, что траектория решения [pic] не является положением
равновесия, но имеет кратную точку, т. е. существуют [pic], такие, что
[pic]. Так как [pic] — не положение равновесия, то [pic]. Поэтому можно
считать, что [pic] при [pic]. Обозначим [pic] и покажем, что [pic] — ?-
Действительно, функция [pic] является решением уравнения (2) при [pic],
причем [pic]. В силу единственности [pic] и [pic] совпадают при всех [pic].
Применяя аналогичное рассуждение к решению [pic], получим, что [pic]
определено при [pic] и функции [pic] и [pic] совпадают при этих t. Таким
образом, можно продолжить [pic] на все [pic], при этом должно выполняться
то есть [pic] — периодическая функция с наименьшим периодом.
Траектория такого решения является замкнутой кривой. Из приведенного
вытекает следующий результат: Каждая траектория автономного уравнения (2)
принадлежит одному из следующих трех типов:
1) положение равновесия;
2) замкнутая траектория, которой соответствует периодическое решение с
положительным наименьшим периодом;
3) траектория без самопересечения, которой соответствует непериодическое
1.3. Предельные множества траекторий.
Определение. Точка [pic] называется ?-предельной точкой траектории
[pic], [pic], если существует последовательность [pic] такая, что [pic] при
[pic]. Множество ? всех ?-предельных точек траектории называется ее ?-
предельным множеством. Аналогично для траектории [pic] при [pic]
определяется понятие ?-предельной точки как предела [pic], а также “-
Определение. Траектория [pic] называется положительно (отрицательно)
устойчивой по Лагранжу (обозн. [pic] ([pic])), если существует компакт
[pic] такой, что [pic] при всех [pic] ([pic]), при которых [pic]
определена. Иными словами, если траектория всегда остается в некоторой
ограниченной области фазового пространства.
Можно показать, что предельное множество устойчивой по Лагранжу
траектории не пусто, компактно и связно.
Траектория [pic] называется устойчивой по Пуассону, если каждая ее
точка является ?-предельной и ?-предельной, т. е. [pic]. Примером
устойчивой по Пуассону траектории является состояние равновесия. Если же
рассматривается траектория, отличная от неподвижной точки, то устойчивой по
Пуассону она будет в том случае, если обладает свойством возвращаться в
сколь угодно малую окрестность каждой своей точки бесконечное число раз.
Поэтому устойчивыми по Пуассону будут циклы и квазипериодические траектории
(суперпозиция двух периодических колебаний с несоизмеримыми частотами), а
также более сложные траектории, возникающие в хаотических системах.
Рассмотрим (без доказательств) некоторые свойства предельных множеств в
1. Предельные множества траекторий автономных систем состоят из целых
2. Если траектория содержит по крайней мере одну свою предельную точку,
то эта траектория замкнутая или представляет собой точку покоя.
3. Если траектория остается в конечной замкнутой области, не содержащей
точек покоя системы, то она либо является циклом, либо спиралевидно
приближается при [pic] к некоторому циклу.
4. Пусть в некоторой окрестности замкнутой траектории [pic] нет других
замкнутых траекторий. Тогда все траектории, начинающиеся достаточно близко
от ?, спиралевидно приближаются к ? при [pic] или при [pic].
Пример. Рассмотрим автономную систему при [pic]:
Для исследования системы удобно в фазовой плоскости ввести полярные
координаты. Тогда получаем следующие уравнения для определения [pic]:
откуда получаем [pic].
Первое из этих уравнений легко интегрируется. Оно имеет решения [pic] и
[pic]. При [pic] решения [pic] монотонно убывают от [pic] до 0, а при [pic]
решения [pic] монотонно возрастают от [pic] до бесконечности. Так как
[pic], то отсюда следует, что при [pic] и [pic] все траектории системы
образуют спирали, раскручивающиеся от окружности [pic] к бесконечно
удаленной точке или к началу координат при неограниченном возрастании
полярного угла. Начало координат является положением равновесия и
одновременно ?-предельным множеством для всех траекторий, у которых [pic].
Если [pic], то ?-предельное множество траектории пусто. Окружность [pic]
является замкнутой траекторией и одновременно ?-предельным множеством для
всех траекторий, отличных от положения равновесия.
1.4. Траектории линейных систем на плоскости.
Рассмотрим автономную линейную однородную систему [pic] (3) с
постоянными коэффициентами. Будем полагать n = 2 и [pic]. В этом
предположении система имеет единственное положение равновесия в начале
координат. С помощью линейного неособого преобразования X = SY приведем
систему (3) к виду [pic],
где J — жорданова форма матрицы A. В зависимости от вида собственных чисел
имеют место следующие случаи:
1) [pic] вещественны, различны и [pic]. В этом случае [pic].
Параметрические уравнения траекторий таковы: [pic]. Координатные полуоси
являются траекториями, соответствующими [pic] или [pic]. При [pic] и [pic]
Картина расположения траекторий при [pic], имеющая специальное название
— узел, изображена на рис. 1а.
2) [pic] вещественны и [pic]. Полученные в случае узла формулы
сохраняют силу. Соответствующая геометрическая картина, называемая седлом,
изображена на рис. 1б.
3) [pic] комплексно-сопряженные. Пусть [pic]. В преобразовании X = SY
[pic], где [pic] и [pic] — линейно независимые собственные векторы,
соответствующие [pic] и [pic]. Так как А вещественна, [pic] и [pic] можно
выбрать комплексно-сопряженными. Тогда и [pic]. Положим [pic], [pic], а в
качестве фазовой плоскости возьмем [pic]. Переменная [pic] связана с Х
соотношением X = SY = = STZ = QZ, где [pic], [pic]. Следовательно, Q —
вещественная неособая матрица. Преобразование приводит к виду
где матрица коэффициентов образует вещественную жорданову форму матрицы А.
Введем полярные координаты [pic], или [pic], [pic]. Имеем: [pic].
Отделяя вещественные и мнимые части, получим:
Следовательно, [pic]. При [pic] траектории образуют спирали (рис. 1в).
Такое положение траекторий называется фокусом. При [pic] все траектории —
окружности. В этом случае получаем центр. В случае центра все решения
системы (3) периодические с периодом 2?/?.
4) [pic]. Жорданова форма матрицы А имеет треугольный вид, а система
преобразуется к виду
Решением этой системы будет функция [pic]. В зависимости от формы
матрицы J получаются два случая: или вырожденный узел (рис. 1г), либо
звездный (дикритический) узел. Дикритический узел возможен лишь в случае
Рис. 1. Поведение траекторий в зависимости от значений собственных чисел
1.5. Линейные однородные системы
с периодическими коэффициентами.
В данном пункте излагается так называемая теория Флоке.
Будем рассматривать систему вида [pic] (4)
где [pic], а матричная функция P(t) удовлетворяет условию P(t + ?) = P(t),
?>0 при всех [pic]. Такие матричные функции будем называть периодическими с
периодом ? или ?-периодическими.
Теорема Флоке. Фундаментальная матрица системы (4) имеет вид
где G — ?-периодическая матрица, R — постоянная матрица.
Матрица В, определяемая равенством [pic], называется матрицей
монодромии. Для нее справедливо [pic]. Она определяется с помощью
фундаментальной матрицы неоднозначно, но можно показать, что все матрицы
монодромии подобны. Часто матрицей монодромии называют ту, которая
порождается нормированной при [pic] фундаментальной матрицей [pic], то есть
Собственные числа [pic] матрицы монодромии называются мультипликаторами
уравнения (4), а собственные числа [pic] матрицы R — характеристическими
показателями. Из определения R имеем [pic], при этом простым
мультипликаторам соответствуют простые характеристические показатели, а
кратным — характеристические показатели с элементарными делителями той же
Характеристические показатели определены с точностью до [pic]. Из [pic]
и формулы Лиувилля следует, что [pic].
Название мультипликатор объясняется следующей теоремой:
Теорема. Число ? является мультипликатором уравнения (4) тогда и только
тогда, когда существует ненулевое решение [pic] этого уравнения такое, что
Следствие 1. Линейная периодическая система (4) имеет нетривиальное
решение периода ? тогда и только тогда, когда по меньшей мере один из ее
мультипликаторов равен единице.
Следствие 2. Мультипликатору [pic] соответствует так называемое
антипериодическое решение [pic] периода ?, т. е. [pic]. Отсюда имеем:
Таким образом, [pic] есть периодическое решение с периодом [pic].
Аналогично, если [pic] (p и q — целые, [pic]), то периодическая система
имеет периодическое решение с периодом [pic].
Пусть [pic], где [pic] — матрица из теоремы Флоке, [pic] — ее жорданова
форма. По теореме Флоке [pic], или [pic], (5)
где [pic] — фундаментальная матрица, [pic] — ?-периодическая матрица. В
структуре фундаментальной матрицы линейной системы с периодическими
коэффициентами характеристические показатели играют ту же роль, что и
собственные числа матрицы коэффициентов в структуре фундаментальной матрицы
линейной системы с постоянными коэффициентами.
Пример. Рассмотрим дифференциальное уравнение второго порядка
где [pic] — ?-периодическая вещественная скалярная функция.
Мультипликаторами уравнения (6) будем называть мультипликаторы
соответствующей линейной системы, т. е. системы
с матрицей [pic]. Так как [pic], то [pic]. Мультипликаторы являются
собственными числами матрицы
где [pic] — решение уравнения (6), удовлетворяющее начальным условиям [pic]
[pic], а [pic] — решение уравнения (6), удовлетворяющее начальным условиям
[pic] [pic]. Пусть [pic] — характеристическое уравнение для определения
мультипликаторов. Так как [pic], то оно принимает вид [pic], где [pic].
2. Устойчивость решений систем
2.1. Устойчивость по Ляпунову.
Вводя определение устойчивости по Лагранжу и Пуассону в пункте 1.3,
описывались свойства одной отдельно взятой траектории. Понятие устойчивости
по Ляпунову характеризует траекторию с точки зрения поведения соседних
траекторий, располагающихся в ее окрестности. Предположим, что система при
старте из начальной точки [pic] порождает траекторию [pic]. Рассмотрим
другую траекторию той же системы [pic], стартовая точка которой близка к
[pic]. Если обе траектории остаются близкими в любой последующий момент
времени, то траектория [pic] называется устойчивой по Ляпунову.
Наглядная иллюстрация устойчивости по Лагранжу, Пуассону и Ляпунову
приводится на рис. 2. Когда говорят просто об устойчивой траектории, то
всегда имеется в виду устойчивость по Ляпунову.
Рис. 2. Качественная иллюстрация устойчивости по Лагранжу (траектория
остается в замкнутой области), по Пуассону (траектория многократно
возвращается в ?-окрестность стартовой точки) и по Ляпунову (две близкие на
старте траектории остаются близкими всегда)
Рассмотрим уравнение [pic] (1)
где [pic] и функция f удовлетворяет в G условию Липшица локально:
[pic] и [pic], где [pic] — константа, не зависящая от выбора точек [pic] и
Предположим, что уравнение (1) имеет решение [pic], определенное при
[pic], и что [pic]. Чтобы перейти к исследованию нулевого решения, выполним
в (1) замену [pic]. В результате получим уравнение
где [pic] определена в области, содержащей множество [pic]. Это уравнение
называется уравнением в отклонениях. Пусть [pic] — решение (2) с начальными
Определение. Решение [pic] уравнения (2) называется устойчивым по
Ляпунову, если для [pic], такое, что при [pic] [pic].
Решение [pic] называется асимптотически устойчивым, если оно устойчиво
по Ляпунову и существует [pic] такое, что [pic] при [pic].
Неустойчивость решения [pic] означает следующее: существуют
положительное [pic], последовательность начальных точек [pic] при [pic], и
последовательность моментов времени [pic] такие, что [pic].
При исследовании вопроса об устойчивости решений часто прибегают к
заменам переменных, позволяющим упростить вид рассматриваемого уравнения.
Сделаем в (2) замену [pic], где функция [pic] определена при всех [pic] и
непрерывна по z при [pic] равномерно относительно [pic], причем [pic].
Пусть уравнение [pic] однозначно разрешимо относительно z: [pic], где [pic]
определена на множестве [pic] и непрерывна по y при [pic] равномерно
относительно [pic]. Пусть уравнение (2) заменой [pic] можно преобразовать в
Лемма. При сделанных предположениях нулевое решение уравнения (2)
устойчиво по Ляпунову, асимптотически устойчиво или неустойчиво тогда и
только тогда, когда соответственно устойчиво по Ляпунову, асимптотически
устойчиво или неустойчиво нулевое решение уравнения [pic].
Пусть уравнение (2) автономно, а его нулевое решение асимптотически
устойчиво. Множество [pic] называется областью притяжения решения [pic].
2.2. Устойчивость линейных однородных систем.
— вещественная система, [pic] — ее произвольное решение. Замена [pic]
приводит (3) к виду [pic], т. е. произвольное решение уравнения (3)
переводится в тривиальное решение того же уравнения. Следовательно, все
решения уравнения (3) устойчивы по Ляпунову, асимптотически устойчивы или
неустойчивы одновременно. Поэтому можно говорить об устойчивости уравнения
(3), понимая под этим устойчивость всех его решений, в частности
Лемма 1. Пусть [pic] и [pic] или [pic], где [pic] — неособая при всех
[pic] матрица, ограниченная по норме вместе с обратной [pic]. Тогда [pic]
ограничена, не ограничена или бесконечно мала по норме при [pic] тогда и
только тогда, когда [pic] обладает таким свойством.
Лемма вытекает из оценки [pic].
Следствие. Пусть [pic], [pic] — нормированная при [pic] фундаментальная
матрица уравнения (3). Любая фундаментальная матрица уравнения (3)
ограничена, не ограничена или бесконечно мала по норме вместе с [pic].
Теорема 1. 1) Для того чтобы уравнение (3) было устойчивым по Ляпунову,
необходимо и достаточно, чтобы его фундаментальные матрицы были ограничены
при [pic]. 2) Для того чтобы уравнение (3) было асимптотически устойчивым,
необходимо и достаточно, чтобы его фундаментальные матрицы были бесконечно
Доказательство. 1) Достаточность. Пусть [pic] ограничена на [pic].
Решение [pic] задается формулой [pic]. (*)
Так как [pic], то [pic]. Следовательно, уравнение (3) устойчиво по
Ляпунову, так как устойчиво его тривиальное решение. Действительно, если
[pic], то при всех [pic] [pic]. (**)
Необходимость. Пусть уравнение (3) устойчиво по Ляпунову. Тогда устойчиво
его тривиальное решение, и выполняется (**). Пусть [pic] фиксировано.
Положим [pic]. Если [pic], то [pic]. Из (*) и (**) имеем [pic], т. е. [pic]
ограничена. Аналогично доказывается ограниченность [pic], а вместе с ними и
2) Достаточность. Пусть [pic] при [pic]. В силу (*) [pic] при всех [pic],
что и дает асимптотическую устойчивость.
Необходимость. Пусть для любых [pic] при [pic]. Положим [pic]. В силу (*)
[pic], следовательно, [pic]. Аналогично доказывается, что [pic], [pic], что
означает [pic] при [pic]. Теорема доказана.
Применим теорему 1 к исследованию устойчивости уравнения (3) с
постоянной матрицей коэффициентов P. Уравнение (3) в этом случае имеет
фундаментальную матрицу [pic], [pic], где [pic] — жорданова форма матрицы
P. По теореме 1, лемме 1 и следствию к ней устойчивость по Ляпунову,
асимптотическая устойчивость и неустойчивость уравнения (3) эквивалентны
соответственно ограниченности, бесконечной малости и неограниченности
матрицы [pic] при [pic]. Отсюда получаем следующую теорему:
Теорема 2. Линейная однородная система с постоянным коэффициентами: 1)
устойчива по Ляпунову тогда и только тогда, когда среди собственных чисел
матрицы коэффициентов нет таких, вещественные части которых положительны, а
число мнимые и нулевые собственные числа либо простые, либо имеют только
простые элементарные делители; 2) асимптотически устойчива тогда и только
тогда, когда все собственные числа матрицы коэффициентов имеют
отрицательные вещественные части.
Ниже рассматриваются необходимые и достаточные условия отрицательности
корней характеристического уравнения линейной однородной системы с
постоянными коэффициентами — критерий Гурвица (Рауса-Гурвица), а также
частотный критерий Михайлова, являющийся геометрическим признаком,
эквивалентным критерию Гурвица.
Определение. Полином [pic], где [pic], [pic], [pic] называется
полиномом Гурвица, если все его корни имеют отрицательные вещественные
Если полином [pic] является полиномом Гурвица, то все [pic].
Составим [pic]-матрицу Гурвица вида
Теорема Гурвица (критерий Гурвица). Для того чтобы полином [pic]
являлся полиномом Гурвица, необходимо и достаточно, чтобы были положительны
все главные диагональные миноры его матрицы Гурвица [pic]:
Если степень полинома [pic] сравнительно большая, то применение
критерия Гурвица становится затруднительным. В этом случае для определения
расположения корней полинома [pic] на комплексной плоскости иногда
оказывается более удобным использование частотного критерия Михайлова.
Определение. Пусть [pic], где [pic], [pic], [pic]. Кривая [pic], [pic]
называется годографом Михайлова функции [pic].
Критерий Михайлова непосредственно следует из леммы:
Лемма 2. Угол поворота в положительном направлении ненулевого вектора
[pic] при [pic] равен [pic], где [pic] — число корней полинома [pic] с
положительной вещественной частью с учетом их кратностей.
Критерий Михайлова. Для того чтобы полином [pic], не имеющий чисто
мнимых корней, являлся полиномом Гурвица, необходимо и достаточно, чтобы
угол поворота в положительном направлении вектора [pic] при [pic] был бы
Замечание. Если полином [pic] есть полином Гурвица степени [pic], то
вектор [pic] монотонно поворачивается в положительном направлении на угол
[pic], то есть годограф Михайлова, выходя из точки [pic] положительной
полуоси [pic], последовательно пересекает полуоси [pic], проходя [pic]
2.3. Устойчивость периодических решений.
Рассмотрим уравнение (3) с периодическими коэффициентами, т. е. [pic],
где [pic]. По формуле (5) предыдущей главы уравнение (4) имеет в
рассматриваемом случае фундаментальную матрицу [pic], где [pic] — неособая
?-периодическая непрерывная матрица, тем самым ограниченная вместе с
обратной, [pic] — жорданова матрица, собственные числа [pic] которой —
характеристические показатели уравнения (4). Из леммы 1 следует, что
характеристические показатели играют при оценке фундаментальной матрицы ту
же роль, что собственные числа [pic], когда [pic] постоянна. Учитывая, что
[pic], где [pic] — мультипликаторы уравнения, получаем следующий результат:
Теорема 3. Линейная однородная система с периодическими коэффициентами:
1) устойчива по Ляпунову тогда и только тогда, когда все ее мультипликаторы
не превышают по модулю единицы, а равные единице по модулю либо простые,
либо им соответствуют простые элементарные делители матрицы монодромии; 2)
асимптотически устойчива тогда и только тогда, когда модули всех
мультипликаторов меньше единицы.
Пример. Рассмотрим уравнение из примера п. 1.5:
Уравнение будем называть устойчивым по Ляпунову, асимптотически устойчивым
или неустойчивым, если таковой является соответствующая ему линейная
система. Мультипликаторы находятся из уравнения [pic]: [pic], где [pic].
Поэтому можно сделать вывод, что при [pic] оба мультипликатора вещественны
и один из них по абсолютной величине больше единицы, а при [pic]
мультипликаторы являются комплексно-сопряженными с модулями, равными
единице. По теореме 3 при [pic] уравнение [pic] неустойчиво, а при [pic]
оно устойчиво по Ляпунову, но не асимптотически.
2.4. Классификация положений равновесия
системы второго порядка.
Исследуем на устойчивость положения равновесия линейной однородной
системы двух уравнений с постоянными коэффициентами. Пусть [pic], где
[pic]. Как было показано в пункте 1.4, тип особой точки такой системы
определяется корнями характеристического уравнения [pic] или [pic]. Его
корни можно найти по формуле
Рассмотрим следующие случаи согласно пункту 1.4.
1) [pic] вещественны, различны и [pic] ([pic]). Параметрические
уравнения траекторий: [pic]. Положение равновесия называется узел. Если
корни [pic] положительны ([pic]), то решения будут неограниченно
возрастать, и особая точка — неустойчивый узел.
Если [pic] отрицательны ([pic]), то решения с ростом времени будут
неограниченно уменьшаться, то есть положение равновесия будет
асимптотически устойчивым. Особая точка — устойчивый узел.
2) [pic] вещественны и [pic] ([pic]). В этом случае одна из траекторий
всегда будет неограниченно возрастать, а другая неограниченно уменьшаться.
Таким образом, седло всегда неустойчиво.
3) [pic] комплексно-сопряженные, но не чисто мнимые ([pic]). Решение в
полярных координатах запишется в виде [pic], где [pic]. Если [pic] ([pic]),
то спирали будут раскручиваться от особой точки, и фокус будет
Если [pic] ([pic]), то особая точка — устойчивый фокус, причем
4) [pic] ([pic]). Особая точка — центр, траектории — окружности, то
есть положение равновесия является устойчивым, но не асимптотически.
5) [pic]. Если [pic], то получаем неустойчивый узел, либо вырожденный,
либо дикритический. Если [pic], положение равновесия будет асимптотически
6) Один из корней равен нулю (например [pic]). Траекториями являются
прямые, параллельные друг другу. Если [pic], то получаем прямую
неустойчивых особых точек. Если [pic], то прямая будет содержать устойчивые
7) Оба корня равны нулю. Тогда [pic]. Особая точка неустойчива.
Пример. Рассмотрим систему [pic]. Положение равновесия находится из
уравнения [pic], или [pic], откуда [pic]. Следовательно, положение
равновесия — неустойчивый узел. Жорданова форма матрицы А имеет вид:
Найдем координаты преобразования [pic], приводящего матрицу А к
жордановой форме, то есть переводящего систему к виду [pic]. Дифференцируя
эти уравнения и подставляя в исходную систему, получаем:
откуда с учетом [pic] [pic], ? — произвольное, [pic], ? — произвольное.
Получаем преобразование [pic]. Определим новое положение осей:
Решение системы [pic] запишется в виде [pic], а исходной системы отсюда
[pic]. Схематическое изображение траекторий:
Рассмотрим теперь некоторые положения равновесия в трехмерном
пространстве. Характеристическое уравнение — кубическое с вещественными
коэффициентами, оно может иметь три вещественных или один вещественный и
два комплексно-сопряженных корня. В зависимости от расположения этих корней
[pic] на плоскости [pic] возможно 10 «грубых» случаев (рис. 3, 1)-5) и 1′)-
5′)) и ряд «вырожденных» (рис. 3, 6)-9)), когда вещественная часть одного
из корней равна нулю или вещественной части не сопряженного с ним корня.
Случаи кратных корней здесь не рассматриваются.
Поведение фазовых траекторий в приведенных случаях показано на рис. 4.
Случаи 1′)-5′) получаются из случаев 1)-5) изменением направления оси t,
так что на рис. 4 надо лишь заменить все стрелки на противоположные.
Устойчивость по Ляпунову в рассмотренных случаях следующая. Все случаи
1′)-5′), а также 2), 5), 8) и 9) неустойчивы. Случаи 1), 3) и 4) устойчивы
асимптотически. Случай 6) устойчив.
Рис. 3. Собственные числа матрицы А. Закрашенным кружком отмечены [pic],
светлым — начало координат.
Рис. 4. Фазовые кривые в трехмерном пространстве.
2.5. Автономные системы на плоскости. Предельные циклы.
Рассмотрим автономную двумерную систему
где [pic] — область.
Предположим, что система (5) имеет замкнутую траекторию [pic] с
наименьшим периодом [pic]. Возьмем произвольную точку [pic] и проведем
через нее нормаль [pic] к [pic] единичной длины. Для определенности
считаем, что [pic] направлен во внешнюю область. Не нарушая общности,
считаем также, что [pic] — начало координат (этого можно добиться заменой
[pic]). Точки на нормали [pic] определяются единственной координатой [pic].
В качестве [pic] берем расстояние от точки нормали до начала координат,
если точка лежит снаружи [pic], и это расстояние, взятое с обратным знаком,
если она лежит внутри [pic].
Рассмотрим траектории [pic], проходящие через точки нормали. Запишем
с неизвестными t, s (? — параметр).
Лемма 3. Существует [pic] такое, что в области [pic] уравнение (6)
имеет единственное решение [pic], удовлетворяющее условиям [pic], причем
функции [pic] непрерывно дифференцируемы при [pic].
Доказательство. Так как [pic] — решение с периодом ?, то по теореме о
дифференцируемости решения функция [pic] определена и непрерывно
дифференцируема по t и ? в некоторой окрестности точки [pic]. Тогда функция
[pic] определена и непрерывно дифференцируема в некоторой окрестности точки
[pic]. Так как [pic] ?-периодична, то [pic]. Рассмотрим якобиан [pic] в
точке [pic]. Имеем [pic]. Следовательно, в точке [pic] [pic], поскольку
[pic] и [pic] — ортогональные векторы. Тогда утверждение леммы вытекает из
теоремы о неявной функции.
Следствие. Справедлива формула
Выясним геометрический смысл функций [pic]. Лемма 3 утверждает, что
каждая траектория, пересекающая нормаль [pic] в точке [pic] из ?-
окрестности начала координат, вновь пересечет ее через промежуток времени
[pic] в точке [pic]. При этом так как функция [pic] также делает полный
оборот вдоль [pic] при [pic], то траектория [pic] также делает полный
оборот при [pic], оставаясь в малой окрестности [pic], если ? достаточно
Функция [pic] называется функцией последования.
Определение. Замкнутая траектория [pic] автономного уравнения (5)
называется устойчивым предельным циклом, если существует такое [pic], что
[pic] является ?-предельным множеством для любой траектории, проходящей
через точку из ?-окрестности кривой [pic].
Определение. Замкнутая траектория [pic] автономного уравнения (5)
называется неустойчивым предельным циклом, если существует такое [pic], что
[pic] является ?-предельным множеством для любой траектории, проходящей
через точку из ?-окрестности кривой [pic].
Так как в реальной действительности время течет в положительном
направлении, то на практике реализуются те периодические движения, которым
соответствуют устойчивые предельные циклы. Такие движения называются
Теорема 4. Пусть [pic]. (7)
Если [pic], то [pic] является устойчивым предельным циклом; если [pic], то
[pic] — неустойчивый предельный цикл.
Характер приближения соседних траекторий к [pic] при [pic] следующий:
они приближаются к [pic], образуя бесконечное число витков спирали, как
изнутри, так и снаружи.
2.6. Устойчивость по первому приближению.
Вернемся к рассмотрению уравнения (1), где [pic]. После замены [pic]
получим уравнение (2), которое, используя разложение в ряд Тейлора, запишем
где [pic] при [pic]. (9)
Теорема 5. Пусть [pic] — постоянная матрица, предельный переход в (9)
выполняется равномерно по [pic] и вещественные части собственных чисел
матрицы [pic] отрицательны. Тогда решение [pic] уравнения (8)
Теорема 6. Пусть [pic] — постоянная матрица, предельный переход в (9)
выполняется равномерно по [pic]. Для устойчивости по Ляпунову нулевого
решения уравнения (8) необходимо, чтобы вещественные части собственных
чисел матрицы [pic] были неположительны.
Рассмотрим теперь автономное уравнение (1): [pic], (10)
где функция [pic] непрерывно дифференцируема при [pic], причем [pic]. Тогда
[pic] является положением равновесия уравнения (10). После замены [pic]
уравнение (10) принимает вид [pic], где [pic], функция [pic] непрерывно
дифференцируема при [pic] и
Из (11) и теорем 5 и 6 вытекает следующее утверждение.
Теорема 7. Если все собственные числа матрицы [pic] имеют отрицательные
вещественные части, то положение равновесия [pic] асимптотически устойчиво;
если же хоть одно из собственных чисел имеет положительную вещественную
часть, то оно неустойчиво.
Пример. Рассмотрим систему двух уравнений [pic] Координаты положений
равновесия определяются из уравнений [pic]. Положения равновесия:
Соответствующие матрицы [pic] имеют вид
Собственные числа определяются уравнением [pic]. При k четном [pic], при k
нечетном [pic]. По теореме 7 при k четном решения [pic] асимптотически
устойчивы, а при k нечетном неустойчивы.
Предположим теперь, что правая часть уравнения (1) и решение [pic]
периодичны по t с одним и тем же периодом ?. Тогда в уравнении (8) [pic],
[pic]. Далее, так как [pic] равномерно непрерывна на компакте [pic], то в
силу периодичности [pic] [pic] выполняется равномерно по [pic]. Поскольку
[pic] — периодическая матрица, то существует замена переменных [pic],
где [pic] — периодическая с периодом ? функция класса [pic], причем [pic],
переводящая уравнение [pic] в [pic] с постоянной матрицей коэффициентов
[pic], определяемой теоремой Флоке. Следовательно, замена (12) переводит
причем функция [pic] определена и непрерывна в области вида [pic]. Условие
(9) также выполняется. Действительно, [pic] в силу (9), ограниченности
[pic] и [pic] и поскольку [pic] эквивалентно [pic]. При этом, как
отмечалось, имеет место равномерность по t.
Согласно лемме из п. 2.1. вопрос об устойчивости тривиального решения
уравнения (8) эквивалентен вопросу об устойчивости тривиального решения
уравнения (13). Так как [pic], где [pic] — собственные числа матрицы [pic],
а [pic] — мультипликаторы линейного уравнения [pic], называемые также
мультипликаторами периодического решения [pic], то из теорем 5 и 6 вытекает
Теорема 8. Если модули всех мультипликаторов периодического решения
периодического уравнения (1) меньше единицы, то это решение асимптотически
устойчиво. Если же модуль хоть одного из мультипликаторов больше единицы,
то оно неустойчиво.
Рассмотрим смешанный случай, когда исследуется устойчивость ?-
периодического решения [pic] автономного уравнения (10). Дифференцируя
тождество [pic], получаем [pic]. Следовательно, функция [pic] является ?-
периодическим решением уравнения в вариациях [pic]. По следствию 1 п. 1.5.
один из мультипликаторов равен единице. Если среди остальных
мультипликаторов имеются такие, модули которых больше единицы, то решение
[pic] неустойчиво по теореме 8. В противном случае теорема 8 неприменима.
Теорема 9. (Андронова-Витта) Если [pic] мультипликаторов периодического
решения уравнения (10) имеют модули, меньшие единицы, то это решение
устойчиво по Ляпунову.
Замечание. Уравнение (10) автономно, поэтому наряду с решением [pic]
имеются и решения [pic], [pic], следовательно, решение [pic] не может быть
2.7. Экспоненциальная устойчивость.
Рассмотрим уравнение (10), в котором [pic]. Обозначим через [pic]
траекторию, проходящую через точку [pic] при [pic]. Предположим, что
нулевое решение (10) асимптотически устойчиво, причем существуют число
[pic] и функция [pic], [pic] при [pic] такие, что [pic] при [pic]. В этом
случае существуют положительные числа [pic] такие, что при [pic]
Если имеет место оценка (14), то говорят, что нулевое решение
экспоненциально асимптотически устойчиво. Например, в условиях теоремы 5
нулевое решение уравнения (8) экспоненциально асимптотически устойчиво.
Более того, нулевое решение уравнения (8) экспоненциально асимптотически
устойчиво при более слабых, чем в теореме 5, ограничениях на нелинейность
[pic]. Достаточно, чтобы левая часть (9) удовлетворяла неравенству [pic],
где [pic] — собственные числа матрицы A (их вещественные части по условию
Для автономного уравнения (10) из экспоненциальной устойчивости следует
асимптотическая устойчивость, и наоборот. Однако для неавтономных систем
справедливо только первое утверждение.
Для неавтономной системы по формуле (14) вводится аналогичное понятие
экспоненциальной устойчивости, однако асимптотическая устойчивость. Кроме
того, справедлив следующая теорема.
Теорема. Для того чтобы линейная система [pic] была экспоненциально
устойчивой, необходимо и достаточно, чтобы существовали две квадратичные
формы [pic] и [pic], обладающие следующими свойствами:
1. [pic] вещественная, симметричная и ограниченная;
2. [pic] вещественная, симметричная и ограниченная;
3. Второй метод Ляпунова.
3.1. Основные определения.
Рассмотрим дифференциальное уравнение
где [pic]. Предположим, что G — область единственности и [pic] при всех
[pic], т. е. уравнение (1) имеет тривиальное решение [pic]. Рассмотрим
вопрос об устойчивости этого решения.
Сущность второго метода Ляпунова заключается в исследовании поведения
некоторой функции [pic] как функции t при замене x на произвольное решение
уравнения (1). В дальнейшем используем определения устойчивости и
асимптотической устойчивости, где [pic].
Под функцией Ляпунова будем понимать любую непрерывную функцию [pic]
такую, что [pic] при всех [pic]. На множестве функций Ляпунова [pic] задан
линейный оператор D, определяемый формулой
[pic] называется производной V в силу уравнения (1). Справедлива
где [pic] — решение уравнения (1) с начальными данными [pic].
Определение. Функция Ляпунова [pic], не зависящая от t, называется
определенно-положительной, если в области G при [pic] [pic]. Функция
Ляпунова [pic] называется определенно-положительной, если существует
определенно-положительная функция [pic] такая, что [pic]. Функция Ляпунова
[pic] называется определенно-отрицательной, если [pic] — определенно-
Определение. Функция Ляпунова [pic] называется положительной, если
[pic] в области G и отрицательной, если [pic] в G.
Таким образом, функцию Ляпунова, тождественно равную в G нулю, можно
рассматривать и как положительную, и как отрицательную.
Отметим следующее свойство определенно-положительных и определенно-
отрицательных функций: если [pic], то [pic]. (4)
Импликация [pic] в (4) вытекает непосредственно из определения функций
Ляпунова. Чтобы обосновать импликацию [pic], рассмотрим произвольную
последовательность [pic], [pic], для которой [pic] при [pic]. Покажем, что
[pic] при [pic]. Предположим, что это неверно. Тогда найдется
подпоследовательность [pic] и положительное число [pic] такие, что [pic].
Согласно определению [pic], где [pic] — определенно-положительная функция.
Положим [pic]. Множество [pic] компактно, поэтому по теореме анализа [pic],
где [pic], следовательно, [pic]. Тогда [pic], что противоречит свойству
3.2. Теоремы второго метода Ляпунова.
Теорема 1. Пусть существует определенно-положительная функция Ляпунова
[pic], такая, что DV есть отрицательная функция. Тогда решение [pic]
уравнения (1) устойчиво по Ляпунову.
Доказательство. Пусть ? — произвольная положительная постоянная, [pic].
Положим [pic] при [pic]. Так как V определенно-положительная, то [pic]. По
l найдем [pic] такое, чтобы [pic]. Рассмотрим решение [pic] при [pic].
Пусть (5) не имеет места. Тогда существует [pic] такое, что [pic], а
при [pic]. В силу (3) и условия теоремы функция [pic] является при [pic]
невозрастающей функцией t. Так как [pic], то [pic], тогда тем более [pic],
что противоречит определению T и тому, что [pic]. Таким образом, импликация
(5) имеет место, а это и означает по определению устойчивость решения [pic]
по Ляпунову. Теорема доказана.
Следствие. Если уравнение (1) имеет в области G определенно-
положительный интеграл, не зависящий от t и уничтожающийся в начале
координат, то решение [pic] устойчиво по Ляпунову.
Теорема 2. Пусть существует определенно-положительная функция Ляпунова
[pic], такая, что DV определенно-отрицательная при [pic]. Тогда решение
[pic] уравнения (1) асимптотически устойчиво.
Доказательство. Условия теоремы 1 выполнены, и решение [pic] устойчиво
по Ляпунову. Следовательно, существует [pic] такое, что
Из определения асимптотической устойчивости в силу (4) заключаем, что
достаточно доказать импликацию [pic] при [pic]. В силу (3) и условия
теоремы [pic] — строго убывающая функция t.
Предположим, что теорема неверна. Тогда
Отсюда, из (6) и (4) следует, что при [pic] [pic]. По условию теоремы
[pic], где [pic] — определенно-положительная функция. Пусть [pic]. Из (3)
следует, что при всех [pic] [pic], что противоречит определенной
положительности [pic]. Полученное противоречие доказывает теорему.
В случае когда уравнение автономно, условия теоремы (2) можно ослабить.
Теорема 3. Пусть уравнение (1) автономно, выполнены условия теоремы 1 и
множество [pic] не содержит целиком полных траекторий уравнения (1), за
исключением положения равновесия [pic]. Тогда решение [pic] асимптотически
Доказательство. Используем доказательство теоремы 2 до формулы (7)
включительно. Далее, пусть [pic] — ?-предельная точка траектории [pic]. Из
определения ?-предельной точки и (7) следует, что [pic]. По первому
свойству предельных множеств (п. 1.3.) все точки траектории [pic] являются
?-предельными для траектории [pic]. Следовательно, для всех t, при которых
определено решение [pic], [pic]. Отсюда и из (3) следует, что при указанных
t [pic], что противоречит условию теоремы, так как [pic] не совпадает с
началом координат. Теорема доказана.
Пример. Рассмотрим уравнение движения диссипативной системы с одной
степенью свободы [pic], где [pic] удовлетворяют условию Липшица при [pic],
[pic] удовлетворяет условию [pic] при [pic] и [pic] при [pic]. Докажем, что
положение равновесия [pic] асимптотически устойчиво.
Соответствующая система двух уравнений имеет вид
В качестве функции Ляпунова возьмем полную энергию системы [pic].
В силу условия [pic] V —определенно-положительная функция, при этом
Следовательно, DV —отрицательная функция и множество M — интервал оси
абсцисс при [pic]. Так как при [pic] при [pic], то множество M не содержит
целых траекторий, отличных от положения равновесия [pic].
По теореме 3 решение [pic] системы асимптотически устойчиво, что и
Перейдем к рассмотрению неустойчивости. Пусть [pic] — функция Ляпунова.
Обозначим через [pic] любую связную компоненту открытого множества [pic] с
началом координат на ее границе.
Теорема 4. Пусть существует функция Ляпунова [pic] такая, что [pic] не
пусто и при [pic]. Тогда решение [pic] уравнения (1) неустойчиво.
Доказательство. Пусть [pic]. Будем рассматривать решения [pic] с
начальной точкой [pic]. Достаточно показать, что для каждого из этих
решений можно указать момент T (для каждого решения свой) такой, что [pic].
Пусть это неверно, т. е. существует решение [pic], удовлетворяющее при
всех [pic] неравенству [pic]. Покажем, что траектория решения [pic]
принадлежит [pic] при [pic]. Действительно, по определению [pic] она может
покинуть область [pic] только через ту часть ее границы, где [pic]. Но это
невозможно, так как [pic] и при возрастании [pic] функция [pic] строго
возрастает, пока [pic], в силу (3).
Итак, доказано, что при [pic] [pic] и [pic]. Следовательно, по условию
теоремы [pic] при [pic]. Интегрируя (3) от [pic] до [pic], получаем
что противоречит ограниченности [pic] при [pic]. Противоречие доказывает
Пример. Рассмотрим уравнение [pic], где [pic] — удовлетворяющая условию
Липшица при [pic] функция такая, что [pic] при [pic]. Докажем
неустойчивость решения [pic].
Рассмотрим систему [pic], соответствующую уравнению примера. В качестве
функции Ляпунова возьмем [pic]. Имеем:
По теореме 4 решение [pic] системы неустойчиво, что и требовалось доказать.
3.3. Устойчивость по первому приближению.
Рассмотрим дифференциальное уравнение
где [pic] — заданная квадратичная форма.
Лемма 1. Если собственные числа матрицы A удовлетворяют условию
то уравнение (8) имеет единственное решение [pic], являющееся квадратичной
В следующих двух леммах будут построены квадратичные формы, являющиеся
функциями Ляпунова для линейного уравнения
и удовлетворяющие условиям теорем 2 и 4.
Лемма 2. Пусть все собственные числа матрицы A имеют отрицательные
вещественные части, [pic] — определенно-отрицательная квадратичная форма.
Тогда уравнение (8) имеет единственное решение [pic], являющееся
определенно-положительной квадратичной формой.
Лемма 3. Пусть матрица A имеет собственные числа с положительными
вещественными частями. Тогда можно подобрать [pic] такое, что существует
единственное решение [pic] уравнения
причем если [pic] — определенно-положительная квадратичная форма, то
область [pic] для квадратичной формы [pic] непуста.
Докажем теперь теоремы 5 и 6 пункта 2.6. Рассмотрим уравнение (1), у
где [pic] удовлетворяет условию
равномерно по [pic].
Теорема 5 (см. теорему 5 п. 2.6). Если все собственные числа матрицы A
имеют отрицательные вещественные части и [pic] удовлетворяет условию (12),
то решение [pic] уравнения (1) асимптотически устойчиво.
Доказательство. Построим функцию Ляпунова, удовлетворяющую условию
теоремы 2 для линейного уравнения (10), и покажем, что она удовлетворяет
условиям теоремы 2 и для уравнения (1).
Пусть [pic] — квадратичная форма, удовлетворяющая уравнению
По лемме 2 [pic] определенно-положительная. Определим ее производную DV в
силу уравнения (1). Из (2) и (11) имеем: [pic]. Отсюда получаем:
Из (12) следует, что для любого [pic] можно указать [pic] такое, что при
[pic] [pic] выполняется [pic]. Так как [pic] — квадратичная форма, то
[pic], [pic], и [pic]. Очевидно также, что [pic]. Из (13) и записанных
неравенств следует, что [pic]. Следовательно, DV — определенно-
отрицательная функция при [pic] [pic], если a выбрать по [pic]. Итак,
выполнены все условия теоремы 2, откуда следует, что решение [pic]
уравнения (1) асимптотически устойчиво. Теорема 5 доказана.
Теорема 6. (см. теорему 6 п. 2.6). Если среди собственных чисел матрицы
имеются такие, вещественные части которых положительны, и выполнено условие
(12), то решение [pic] уравнения (1) неустойчиво.
Доказательство. С помощью леммы 3 построим квадратичную форму [pic],
удовлетворяющую уравнению [pic], и такую, что область [pic] для функции V
непуста. Составим DV в силу уравнения (1). Имеем
Используя (12), как и при доказательстве теоремы 5, покажем, что если a
достаточно мало, то при [pic] [pic] функция [pic]. Следовательно, так как в
области [pic] [pic], то при [pic], [pic] имеем [pic]. Таким образом,
выполнены все условия теоремы 4, откуда и следует, что нулевое решение
уравнения (1) неустойчиво. Теорема доказана.
1. Метод функций Ляпунова в анализе динамики систем. Сб. статей.
Новосибирск: Наука, 1987.
2. М. Розо. Нелинейные колебания и теория устойчивости. М.: Наука, 1971.
3. Б. П. Демидович. Лекции по математический теории устойчивости. М.:
4. И. Г. Петровский. Лекции по обыкновенным дифференциальным уравнениям.
5. Ю. Н. Бибиков. Курс обыкновенных дифференциальных уравнений. М.:
Высшая школа, 1991.
6. В. И. Арнольд. Обыкновенные дифференциальные уравнения. М.: Наука,
7. Кузнецов С. П. Динамический хаос (курс лекций). М.: Изд. ФМЛ, 2001.
💡 Видео
Дополнительные главы ИДУ: Устойчивость линейных систем дифференциальных уравнений | Занятие 1Скачать

ЗАЧЕМ НУЖНЫ ЭТИ... производные! Математика на QWERTY.Скачать

Устойчивость линейных систем дифференциальных уравненийСкачать

Устойчивость линейных систем дифференциальных уравненийСкачать

ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

ДУ Практика по устойчивостиСкачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Устойчивость решений линейных системСкачать


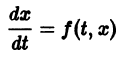
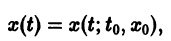
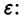
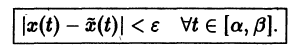
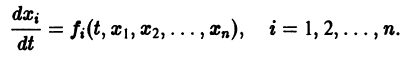
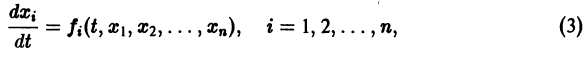
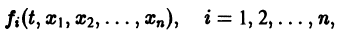
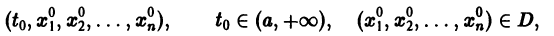
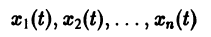
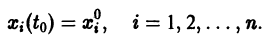
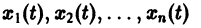
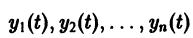
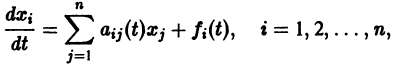
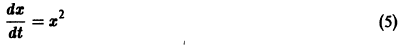
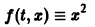
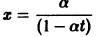
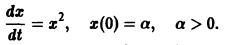
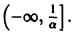
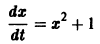


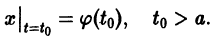
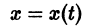
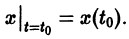


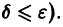
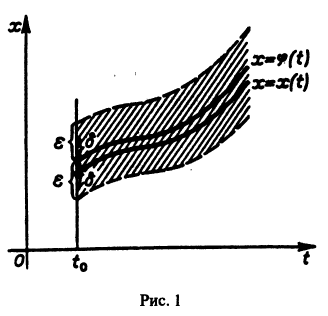
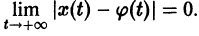

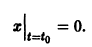
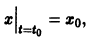
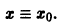
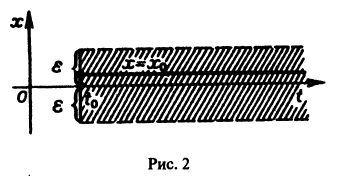
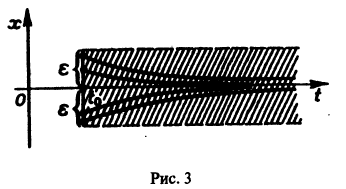
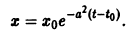
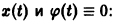
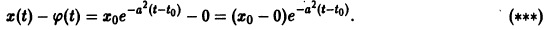
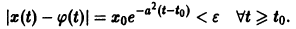
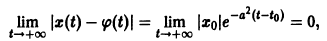
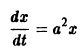
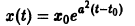
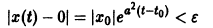
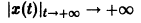
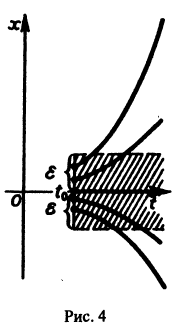
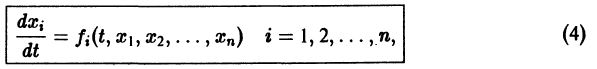
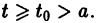
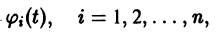
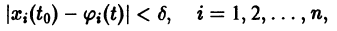
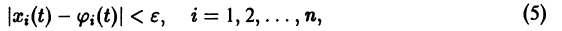
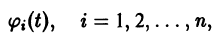
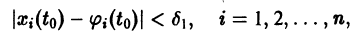
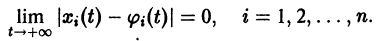


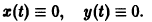
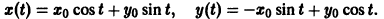
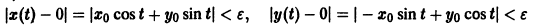
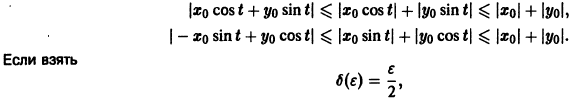
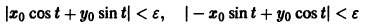
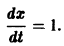
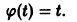
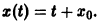
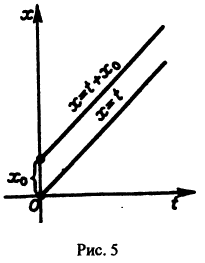


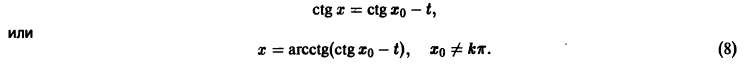
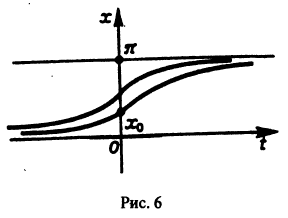
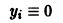
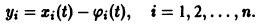

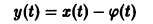
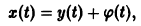

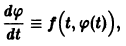
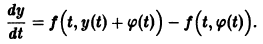

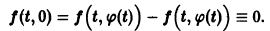
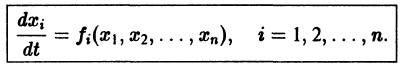
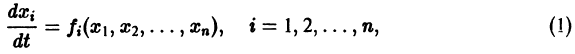
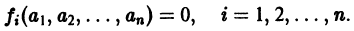
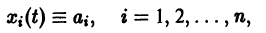
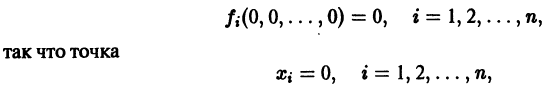
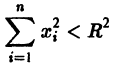
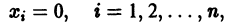
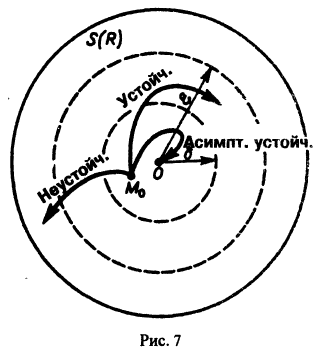
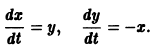
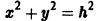
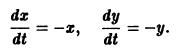
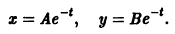
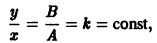
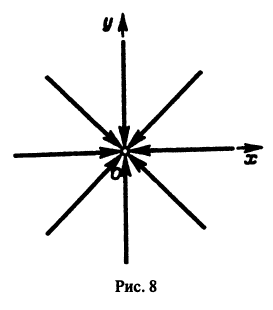
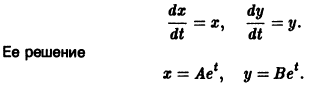
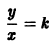
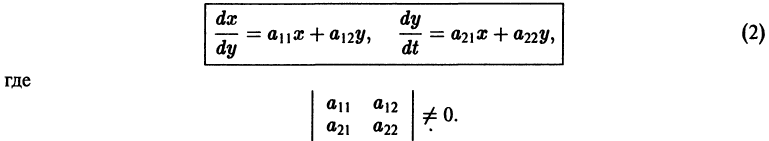
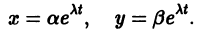
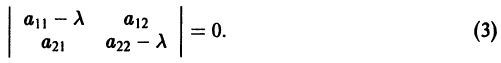
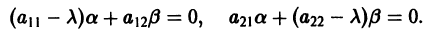
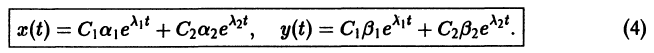
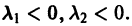 Точка покоя (0,0) в этом случае асимптотически устойчива, так как из-за наличия множителей
Точка покоя (0,0) в этом случае асимптотически устойчива, так как из-за наличия множителей  все точки каждой траектории, находившиеся в начальный момент
все точки каждой траектории, находившиеся в начальный момент  в произвольной
в произвольной 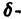 окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой,
окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой, 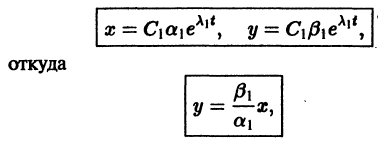
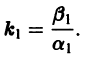
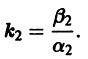
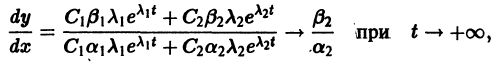
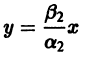
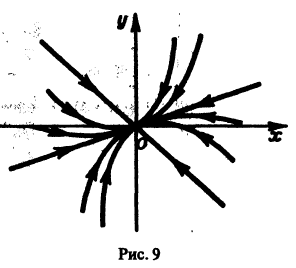
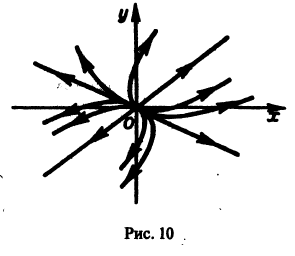
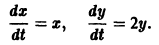
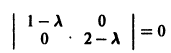
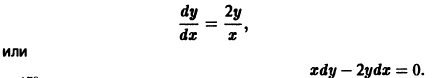

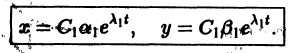
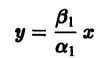
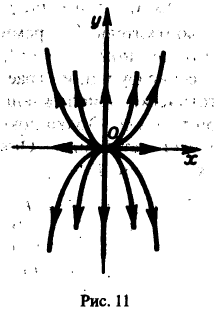
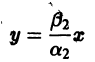
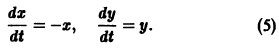
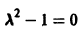
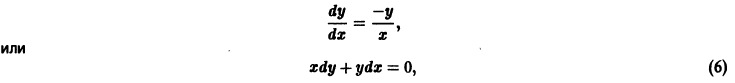
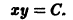
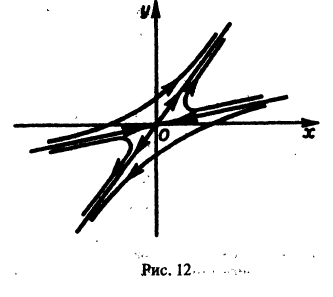
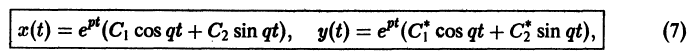
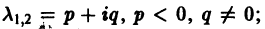 в этом случае множитель
в этом случае множитель 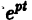 стремится к нулю при
стремится к нулю при 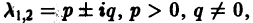 то этот случай переходит в предыдущий при замене t на -t. Траектории не отличаются от траекторий предыдущего случая, но движение по ним при возрастании t происходит в противоположном направлении. Точка покоя неустойчива — неустойчивый фокус.
то этот случай переходит в предыдущий при замене t на -t. Траектории не отличаются от траекторий предыдущего случая, но движение по ним при возрастании t происходит в противоположном направлении. Точка покоя неустойчива — неустойчивый фокус.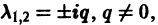 то решения системы (2) — периодические функции. Траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром (рис. 14). Центр является устойчивой точкой покоя, однако асимптотической устойчивости нет, так как решение
то решения системы (2) — периодические функции. Траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром (рис. 14). Центр является устойчивой точкой покоя, однако асимптотической устойчивости нет, так как решение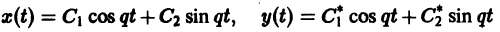
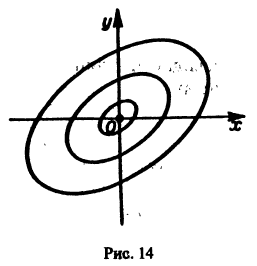
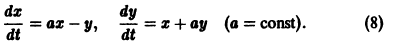
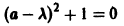
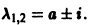

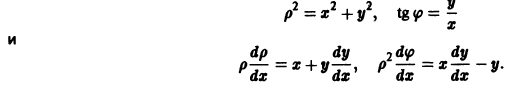
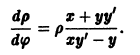

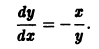
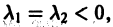 то из-за наличия множителя
то из-за наличия множителя 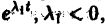 решения х(t), y(t) стремятся к нулю при
решения х(t), y(t) стремятся к нулю при 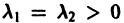 замена t на -t приводит к предыдущему случаю, но движение по траекториям происходит в противоположном направлении. Точка покоя в этом случае называется неустойчивым вырожденным узлом.
замена t на -t приводит к предыдущему случаю, но движение по траекториям происходит в противоположном направлении. Точка покоя в этом случае называется неустойчивым вырожденным узлом.