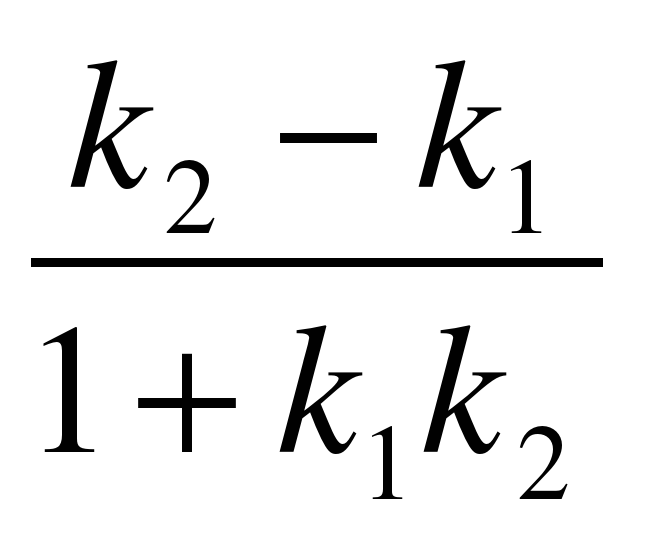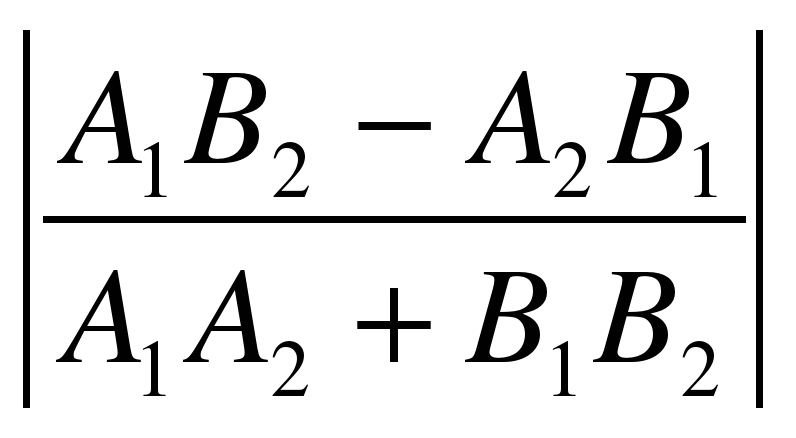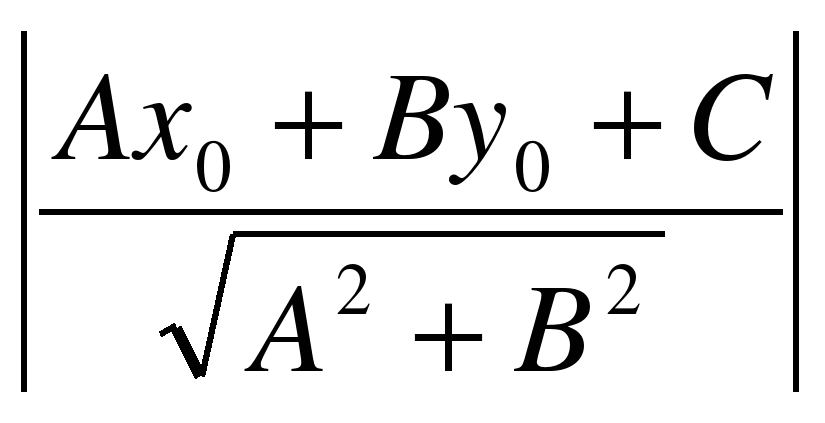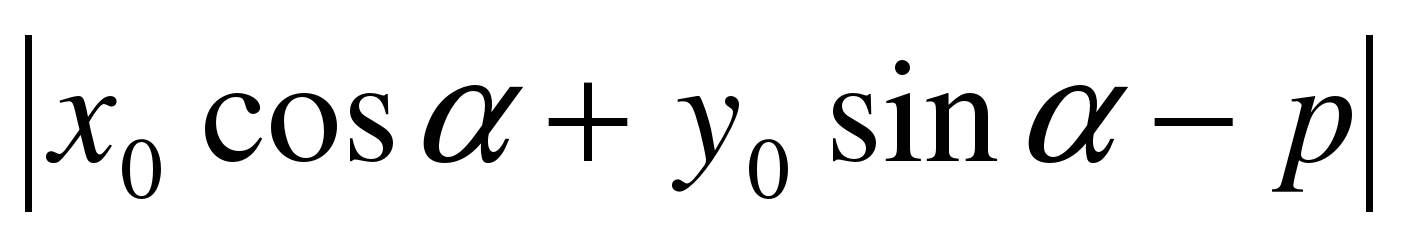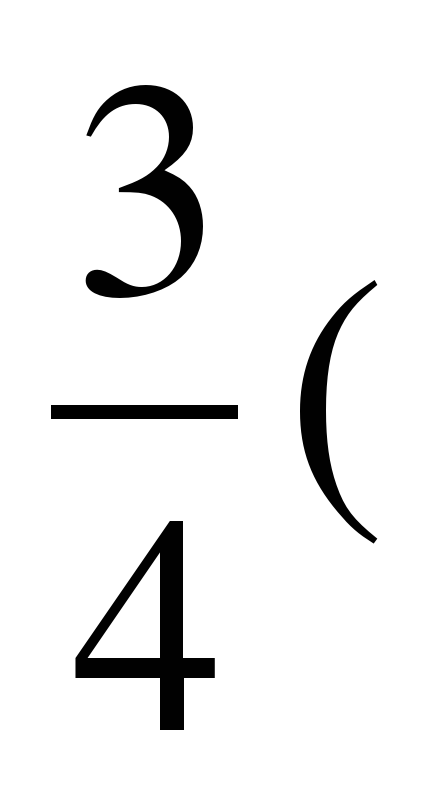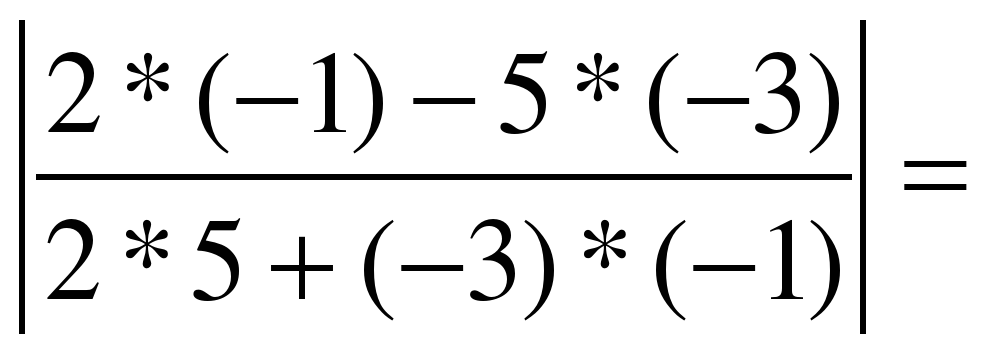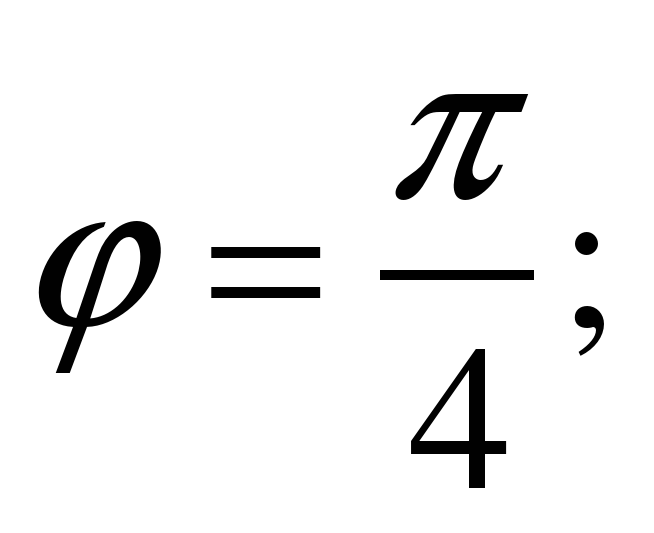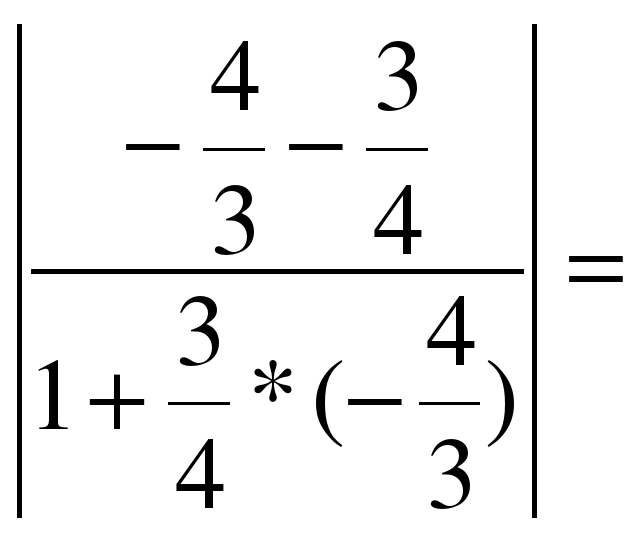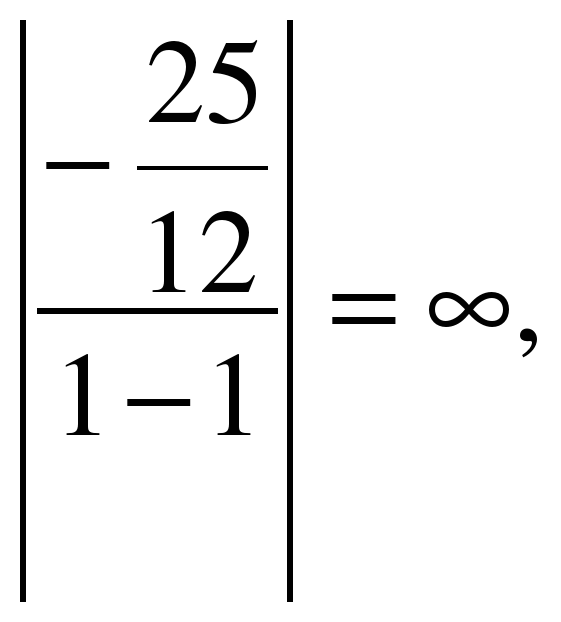С помощю этого онлайн калькулятора можно найти точку пересечения прямых в пространстве. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
- Предупреждение
- Точка пересечения прямых в пространстве − теория, примеры и решения
- 1. Точка пересечения прямых в пространстве, заданных в каноническом виде.
- 2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.
- 3. Точка пересечения прямых в пространстве, заданных в разных видах.
- 4. Примеры нахождения точки пересечения прямых в пространстве.
- ГДЗ учебник по алгебре 7 класс Мордкович. §10. Взаимное расположение графиков линейных функций. Номер №10.1.
- ГДЗ учебник по алгебре 7 класс Мордкович. §10. Взаимное расположение графиков линейных функций. Номер №10.1.
- Решение а
- Решение б
- Решение в
- Решение г
- Взаимное расположение плоскостей
- Взаимное расположение прямых
- Просмотр содержимого документа «Взаимное расположение прямых»
- 🎬 Видео
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:15. Взаимное расположение прямых в пространствеСкачать

Точка пересечения прямых в пространстве − теория, примеры и решения
- Содержание
- 1. Точка пересечения прямых, заданных в каноническом виде.
- 2. Точка пересечения прямых, заданных в параметрическом виде.
- 3. Точка пересечения прямых, заданных в разных видах.
- 4. Примеры нахождения точки пересечения прямых в пространстве.
1. Точка пересечения прямых в пространстве, заданных в каноническом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2:
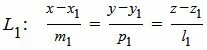 , , | (1) |
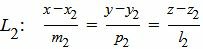 , , | (2) |
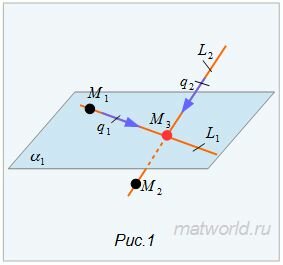
Найти точку пересечения прямых L1 и L2 (Рис.1).
 |
Запишем уравнение (1) в виде системы двух линейных уравнений:
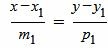 , , | (3) |
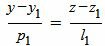 | (4) |
Сделаем перекрестное умножение в уравнениях (3) и (4):
| p1(x−x1)=m1(y−y1) |
| l1(y−y1)=p1(z−z1) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p1x−m1y=p1x1−m1y1, | (5) |
| l1y−p1z=l1y1−p1z1. | (6) |
Аналогичным образом преобразуем уравнение (2):
Запишем уравнение (2) в виде системы двух линейных уравнений:
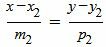 , , | (7) |
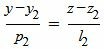 | (8) |
Сделаем перекрестное умножение в уравнениях (7) и (8):
| p2(x−x2)=m2(y−y2) |
| l2(y−y2)=p2(z−z2) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p2x−m2y=p2x2−m2y2, | (9) |
| l2y−p2z=l2y2−p2z2. | (10) |
Решим систему линейных уравнений (5), (6), (9), (10) с тремя неизвестными x, y, z. Для этого представим эту систему в матричном виде:
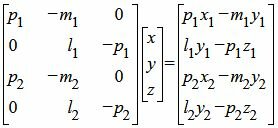 | (11) |
Как решить систему линейных уравнений (11)(или (5), (6), (9), (10)) посмотрите на странице Метод Гаусса онлайн. Если система линейных уравнениий (11) несовместна, то прямые L1 и L2 не пересекаются. Если система (11) имеет множество решений, то прямые L1 и L2 совпадают. Единственное решение системы линейных уравнений (11) указывает на то, что это решение определяет координаты точки пересечения прямых L1 и L2 .
2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2 в параметрическом виде:
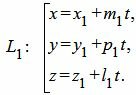 | (12) |
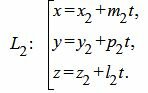 | (13) |
Задачу нахождения нахождения точки пересечения прямых L1 и L2 можно решить разными методами.
Метод 1. Приведем уравнения прямых L1 и L2 к каноническому виду.
Для приведения уравнения (12) к каноническому виду, выразим параметр t через остальные переменные:
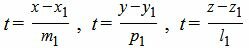 | (14) |
Так как левые части уравнений (14) равны, то можем записать:
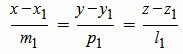 | (15) |
Аналогичным образом приведем уравнение прямой L2 к каноническому виду:
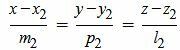 | (16) |
Далее, для нахождения точки пересечения прямых, заданных в каноническом виде нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямых L1 и L2 решим совместно уравнения (12) и (13). Из уравнений (12) и (13) следует:
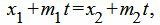 | (17) |
 | (18) |
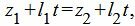 | (19) |
Из каждого уравнения (17),(18),(19) находим переменную t. Далее из полученных значений t выбираем те, которые удовлетворяют всем уравнениям (17)−(19). Если такое значение t не существует, то прямые не пересекаются. Если таких значений больше одного, то прямые совпадают. Если же такое значение t единственно, то подставляя это зачение t в (12) или в (13), получим координаты точки пересечения прямых (12) и (13).
3. Точка пересечения прямых в пространстве, заданных в разных видах.
Если уравнения прямых заданы в разных видах, то можно их привести к одному виду (к каноническому или к параметрическому) и найти точку пересечения прямых, описанных выше.
4. Примеры нахождения точки пересечения прямых в пространстве.
Пример 1. Найти точку пересечения прямых L1 и L2:
 | (20) |
 | (21) |
Представим уравнение (20) в виде двух уравнений:
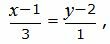 | (22) |
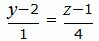 | (23) |
Сделаем перекрестное умножение в уравнениях (22) и (23):
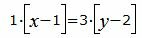 |
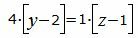 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
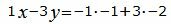 |
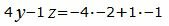 |
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
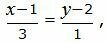 | (26) |
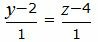 | (27) |
Сделаем перекрестное умножение в уравнениях (7) и (8)
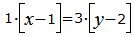 |
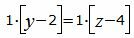 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
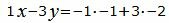 |
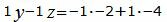 |
Решим систему линейных уравнений (24), (25), (28), (29) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
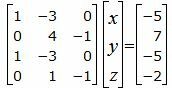 | (30) |
Решим систему линейных уравнений (30) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
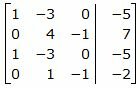 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1:
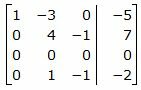 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 4 со строкой 2, умноженной на −1/4:
 |
Сделаем перестановку строк 3 и 4.
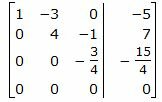 |
Второй этап. Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строку 2 со строкой 3, умноженной на −4/3:
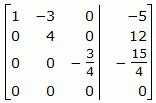 |
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 3/4:
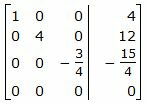 |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
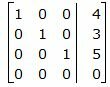 |
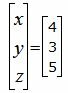 |
Ответ. Точка пересечения прямых L1 и L2 имеет следующие координаты:
Пример 2. Найти точку пересечения прямых L1 и L2:
 | (31) |
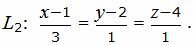 | (32) |
Приведем параметрическое уравнение прямой L1 к каноническому виду. Выразим параметр t через остальные переменные:
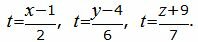 |
Из равентсв выше получим каноническое уравнение прямой:
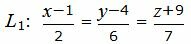 | (33) |
Представим уравнение (33) в виде двух уравнений:
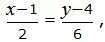 | (34) |
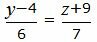 | (35) |
Сделаем перекрестное умножение в уравнениях (34 и (35):
 |
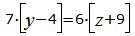 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
 |
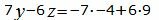 |
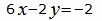 | (36) |
 . . | (37) |
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
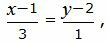 | (38) |
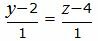 | (39) |
Сделаем перекрестное умножение в уравнениях (38) и (39)
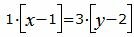 |
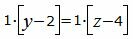 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
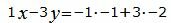 |
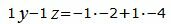 |
Решим систему линейных уравнений (36), (37), (40), (41) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
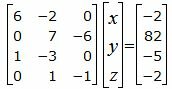 | (42) |
Решим систему линейных уравнений (42) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1/6:
 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строки 3 и 4 со строкой 2, умноженной на 8/21 и −1/7, соответственно:
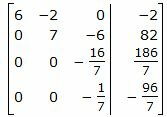 |
Исключим элементы 3-го столбца матрицы ниже элементаa33. Для этого сложим строку 4 со строкой 3, умноженной на -1/16:
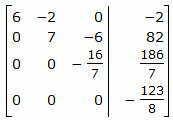 |
Из расширенной матрицы восстановим последнюю систему линейных уравнений:
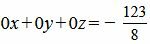 | (43) |
Уравнение (43) несовместна, так как несуществуют числа x, y, z удовлетворяющие уравнению (43). Следовательно система линейных уравнений (42) не имеет решения. Тогда прямые L1 и L2 не пересекаются. То есть они или параллельны, или скрещиваются.
Прямая L1 имеет направляющий вектор q1=, а прямая L2 имеет направляющий вектор q2=. Эти векторы не коллинеарны. Следовательно прямые L1 и L2 скрещиваются .
Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

ГДЗ учебник по алгебре 7 класс Мордкович. §10. Взаимное расположение графиков линейных функций. Номер №10.1.
Не выполняя построения, установите взаимное расположение графиков линейных функций:
а ) y = 2 x и y = 2 x − 4 ;
б ) y = x + 3 и y = 2 x − 1 ;
в ) y = 4 x + 6 и y = 4 x + 6 ;
г ) y = 12 x − 4 и y = −x + 1 .
Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

ГДЗ учебник по алгебре 7 класс Мордкович. §10. Взаимное расположение графиков линейных функций. Номер №10.1.
Решение а
y = 2 x и y = 2 x − 4
Прямые параллельны. Прямая y = 2 x − 4 ниже прямой y = 2 x на 4 единицы по оси Oy.
Решение б
y = x + 3 и y = 2 x − 1
x + 3 = 2 x − 1
2 x − x = 3 + 1
x = 4
y = x + 3
y = 4 + 3
y = 7
Прямые пересекаются в точке ( 4 ; 7 ).
Решение в
y = 4 x + 6 и y = 4 x + 6
Это одна и та же прямая.
Решение г
y = 12 x − 4 и y = −x + 1
12 x − 4 = −x + 1
12 x + x = 1 + 4
13 x = 5
Видео:Геометрия 10 класс (Урок№5 - Взаимное расположение прямых в пространстве.)Скачать

Взаимное расположение плоскостей
Данный калькулятор предназначен для определения взаимного расположения двух плоскостей в пространстве онлайн.
Две плоскости могут иметь три варианта взаимного расположения относительно друг друга. Во-первых, плоскости могут быть параллельны. Во-вторых, они могут быть перпендикулярны. В таком случае угол между плоскостями равен 90 градусам. В-третьих, плоскости могут пересекаться, образовывая при этом два острых и два тупых угла.
Таким образом, с помощью данного калькулятора определяется следующее: пересекаются или нет плоскости, и, если они пересекаются, то перпендикулярны ли они.
Чтобы ответить на вопрос о взаимном расположении плоскостей, необходимо ввести уравнения заданных плоскостей в калькулятор и нажать кнопку «Вычислить».
Видео:Взаимное расположение прямых на плоскости. 7 класс.Скачать

Взаимное расположение прямых
Угол между двумя прямыми, условия параллельности и перпендикулярности двух прямых, пересечение прямых, расстояние от данной точки до данной прямой.
Просмотр содержимого документа
«Взаимное расположение прямых»
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ.
Угол между двумя прямыми, условия параллельности и перпендикулярности двух прямых, пересечение прямых, расстояние от данной точки до данной прямой.
Под углом между прямыми в плоскости понимают меньший (острый) из двух смежных углов образованными этими прямыми.
Если прямые l1 и l2 заданы уравнениями с угловыми коэффициентами у=к1х+b1 и у=к2х+b2, то угол φ между ними вычисляется по формуле
tg φ=
Условие параллельности прямых l1 и l2 имеет вид
а условие их перпендикулярности
k1 = — 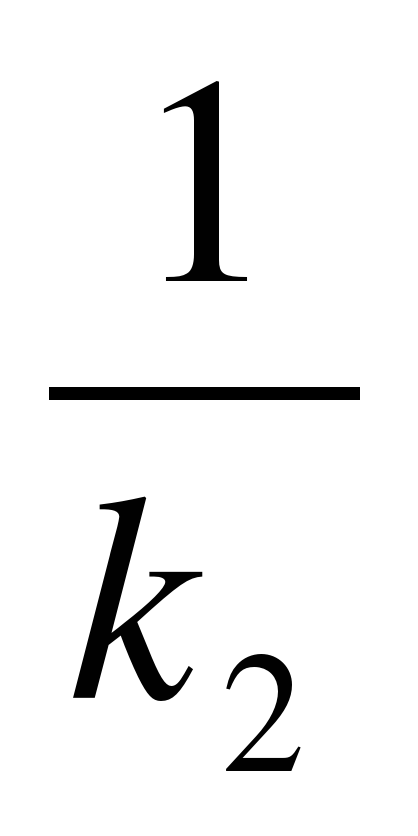
то величина φ угла между ними вычисляется по формуле
tg φ=
угловые их параллельности
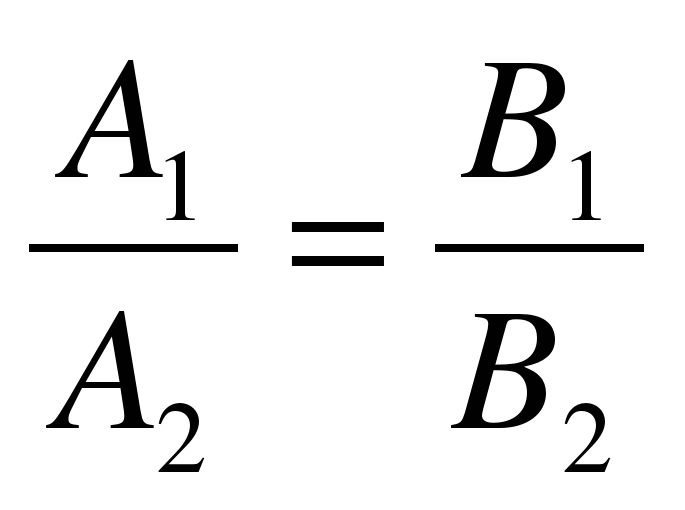
Условие их перпендикулярности
Для нахождения общих точек прямых l1 и l2 необходимо решить систему

Если 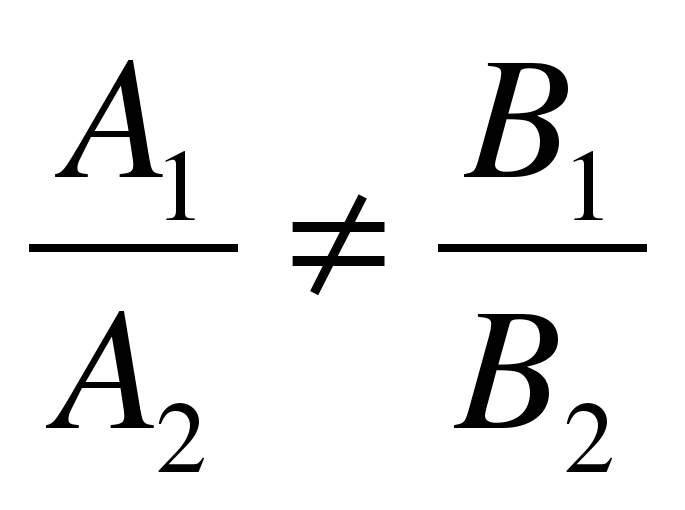
Если 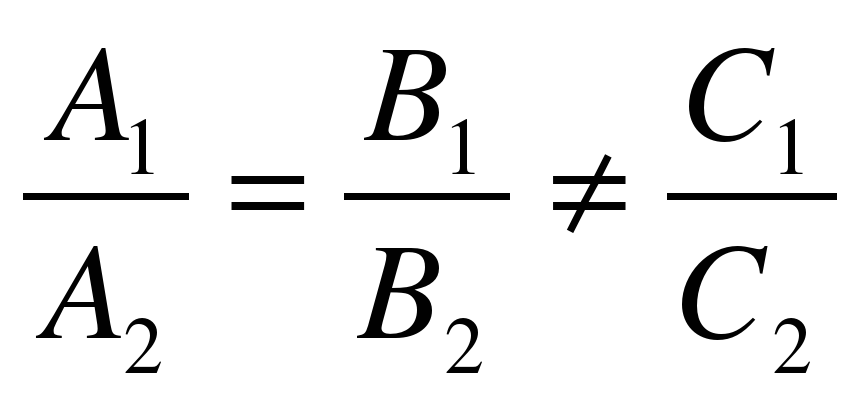
Если 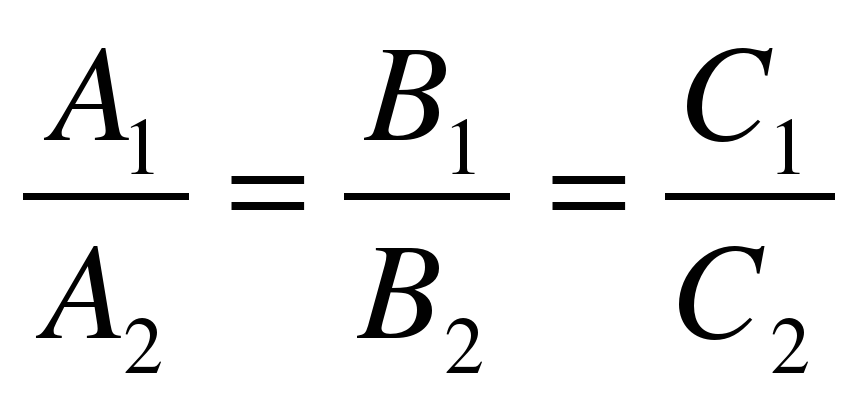
Расстоянием d от точки М0 (х0;у0) до прямой Ах+Ву+С=0 называется длина перпендикуляра , опущенного из этой точки на прямую .
Расстояние d определяется по формуле
d=
Расстояние от точки М0 (х0;у0) до прямой х cos 

d=
ПРИМЕР: найти угол между прямыми :
1) y=2x-3 и y=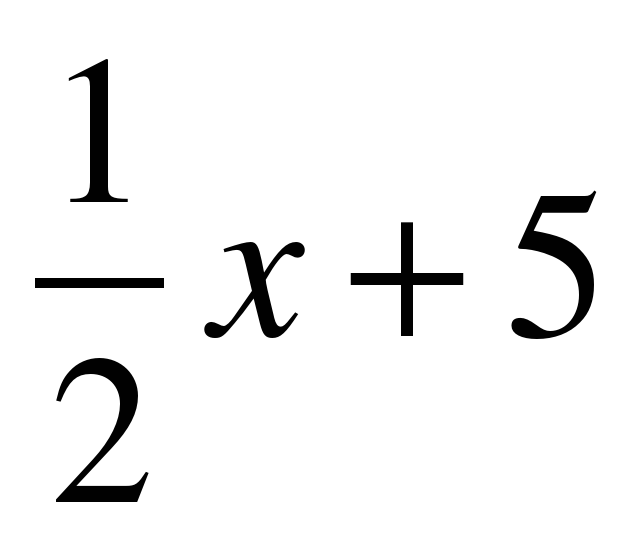
2) 2x-3y+10=0 и 5x – y+4=0;
3) y= 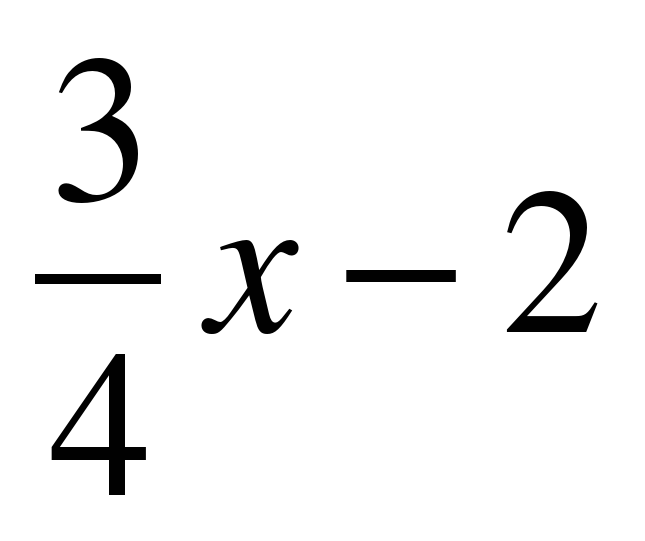
Воспользуемся формулой. Подставляя в неё значения k1=2 и k2= 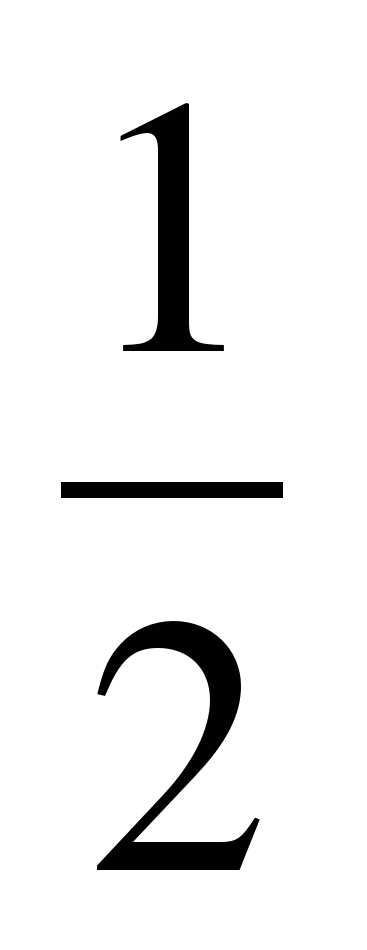

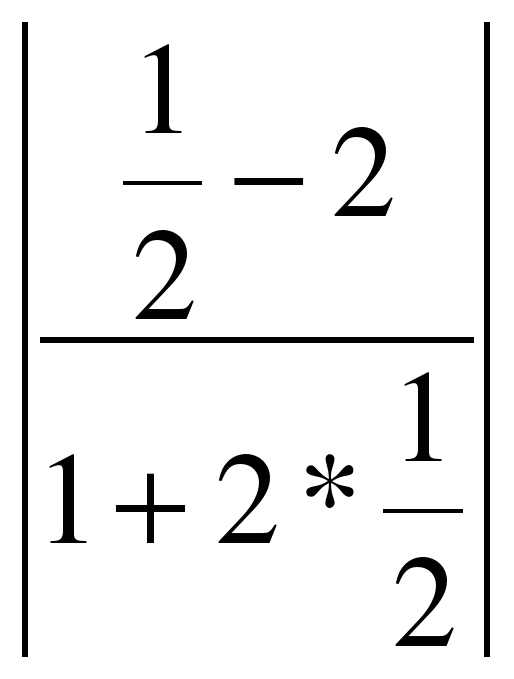
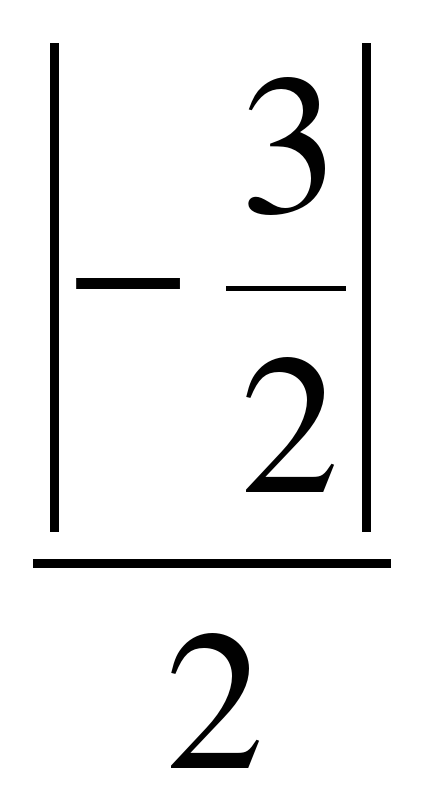

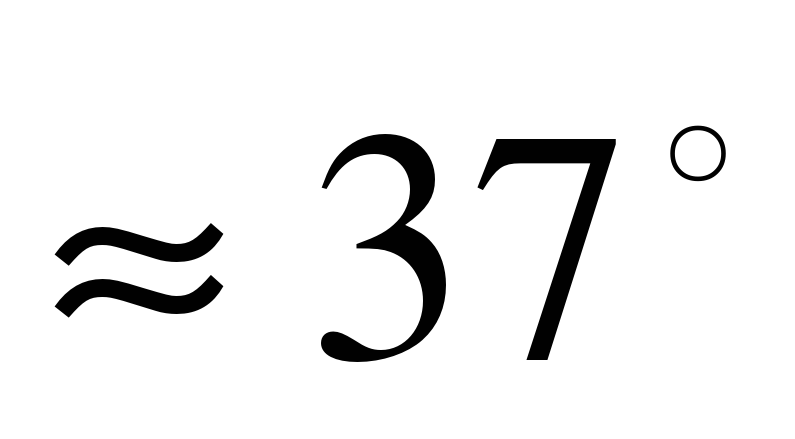
Подставим значения А1 = 2, В1=-3,А2=5,В2=-1 в формулу : tg
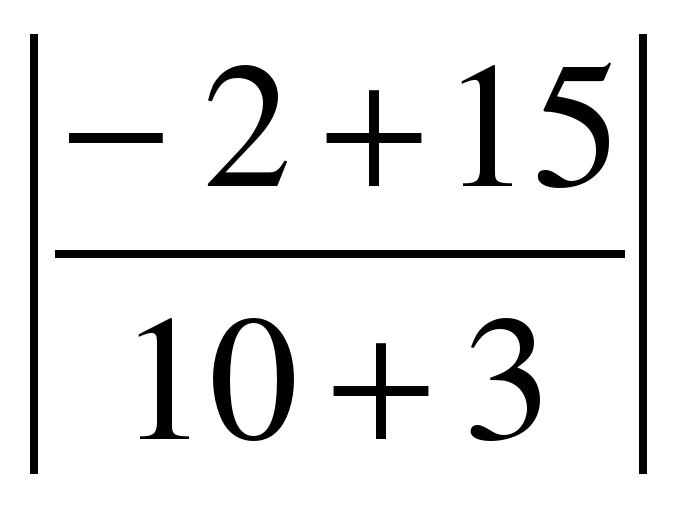
Здесь k1=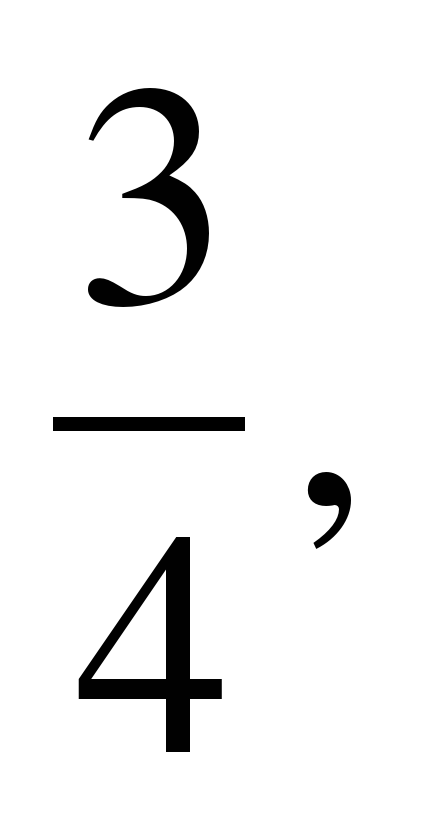
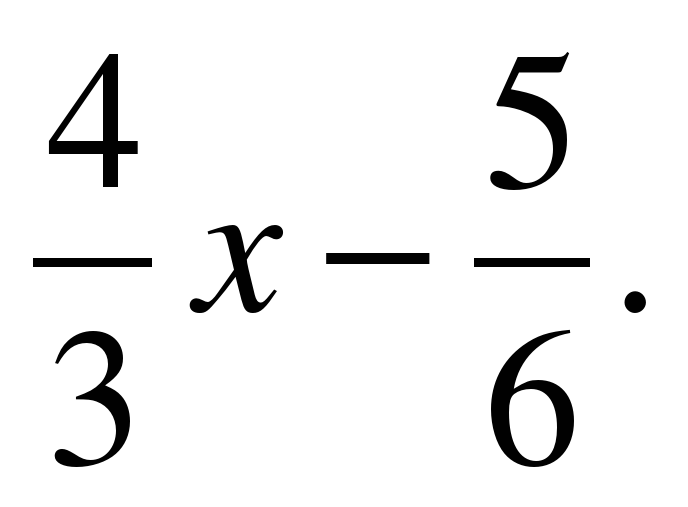
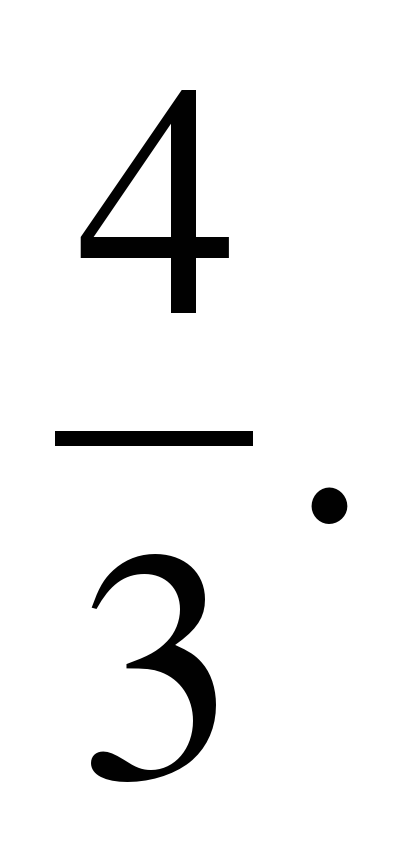


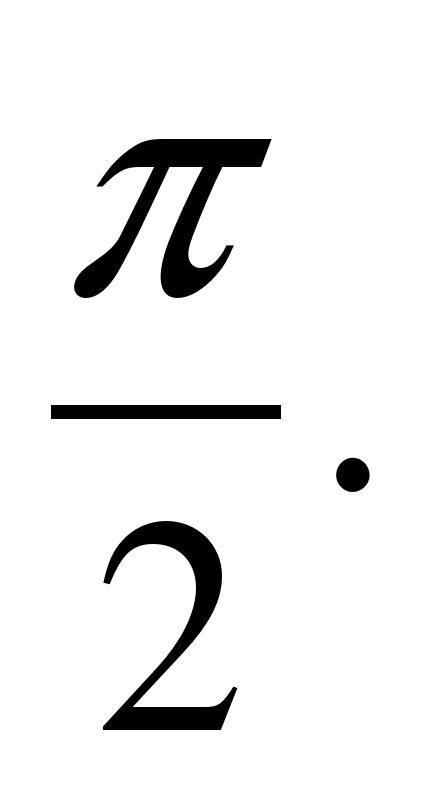
k1=5,k2=5, tg

Задания для практических занятий:
1. Найти угол между прямыми:
2) 2х-3у-7=0 и 2х-у+5=0;
3) у=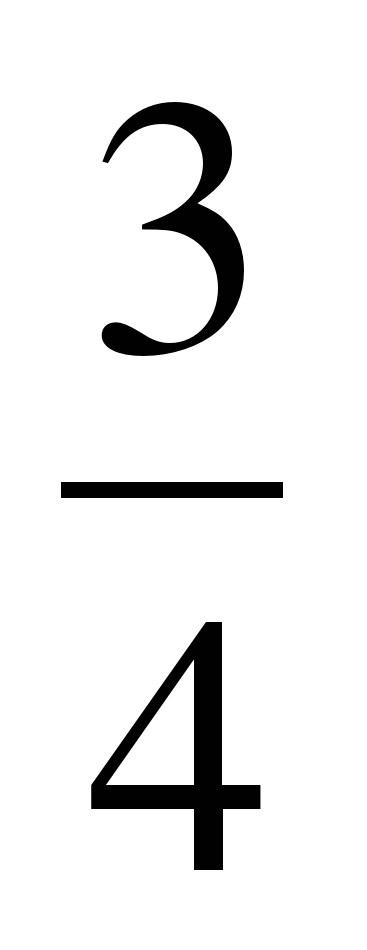
4) у= 7х -1 и у=7х+1;
2. Исследовать взаимное расположение следующих пар прямых:
1) 3х+5у-9=0 и 10х-6у+4=0
2) 2х+5у-2=0 и х+у+4=0;
3) 2у=х-1 и 4у-2х+2=0;
5) 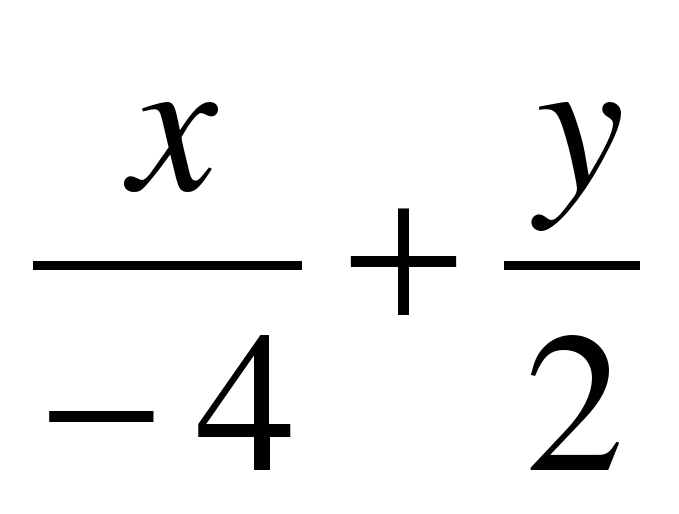
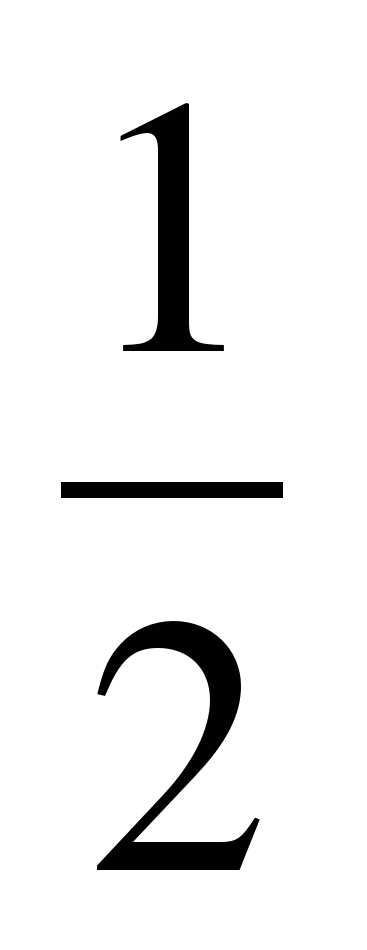
8) у=3-6х и 12х+2у-5=0;
10) 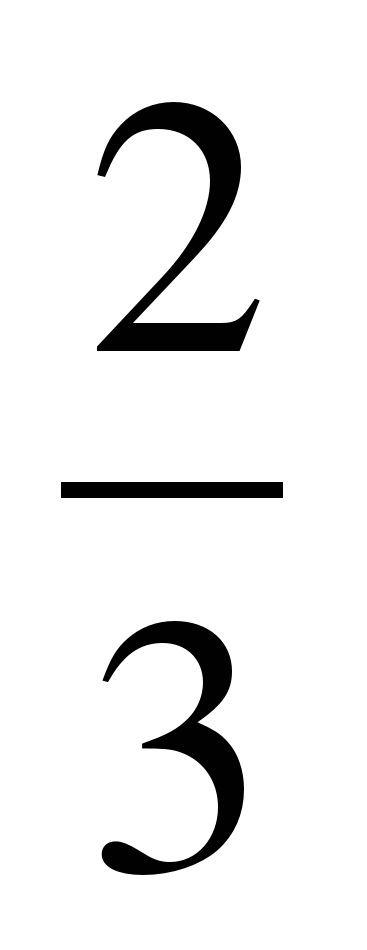
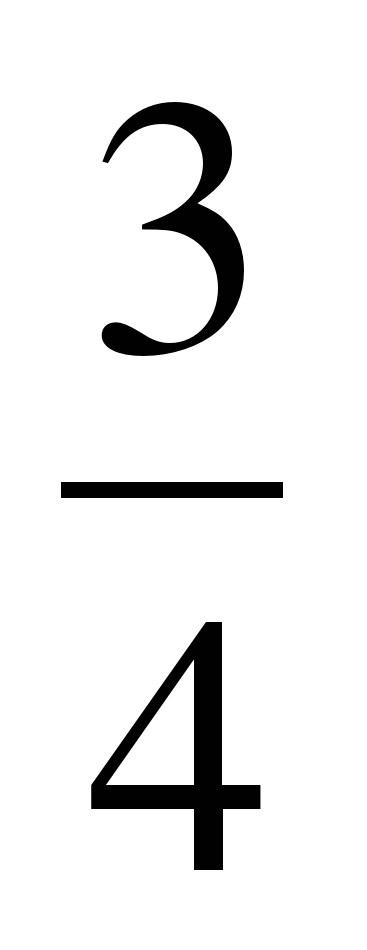
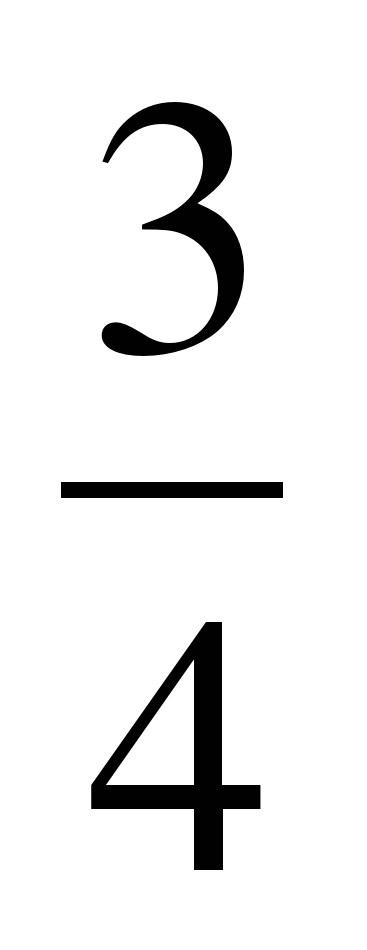
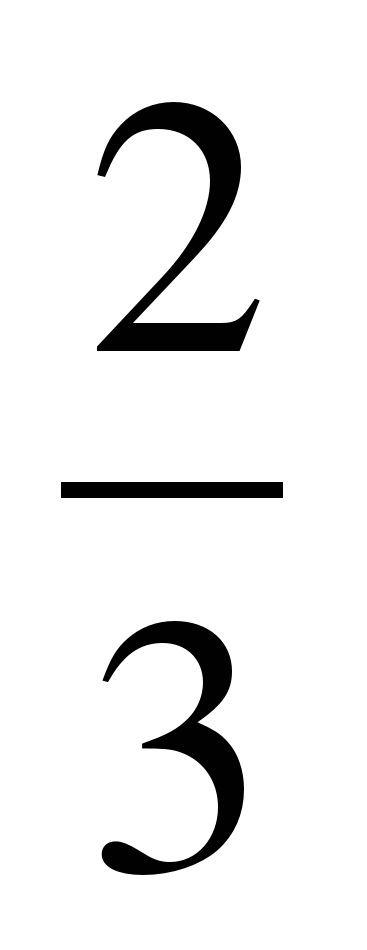
3. При каких значениях 
1) 2х-3у+4=0 и 
2) 
3) 4х+у-6=0 и 3х+
4) х- 
4.Через точку пересечения прямых 3х-2у+5=0; х+2у-9=0 проведена прямая, параллельная прямой 2х+у+6=0. Составить ее уравнение.
5. Найти уравнение прямой, проходящий через точку А (-1;2):
а) параллельно прямой у=2х-7;
б) перпендикулярно прямой х+3у-2=0.
6. Найти длину высоты ВД в треугольнике с вершинами А (4;-3); В (-2;6) и С (5;4).
7. Даны уравнения сторон треугольника: х+3у-3=0, 3х-11у-29=0 и 3х-у+11=0.
Найти вершины этого треугольника.
Задания для самостоятельного решения
1. Найти острый угол между прямыми:
2) 2х-3у+6=0 и 3х-у-3=0
4) 3х+4у-12=0 и 15х-8у-45=0
2. Исследовать взаимное расположение следующих пар прямых:
1) 2х-3у+4=0 и 10х+3у-6=0
2) 3х-4у+12=0 и 4х+3у-6=0
3) 25х+20у-8=0 и 5х+4у+4=0
4) 4х+5у-8=0 и 3х-2у+4=0
3. Найти уравнение прямой, проходящий через точку В (2;-3)
а) параллельно прямой, соединяющей точки М1 (-4;0) и М2 (2;2);
б) перпендикулярно прямой х-у=0.
4. Составить уравнение прямой, содержащий высоту ВД в треугольнике с вершинами
А (-3;2), В (5;-2), С (0; 4)
5. Найти площадь треугольника, образованного прямыми 2х+у+4=0, х+7у-11=0 и 3х-5у-7=0.
6.Через точку пересечения прямых 3х+2у-4=0 и х-5у+8=0 проведены прямые, одна из которых проходит через начало координат, а другая параллельна оси Ох. Составить их уравнения.
7. Дан четырехугольник АВСД с вершинами А (3;5); В (6;6); С (5;3); Д (1;1). Найти:
а) координаты точки пересечения диагоналей;
б) угол между диагоналями.
8.Даны вершины треугольника А(2;-2), В (3;5), С (6;1). Найти:
1) длины сторон АС и ВС;
2) уравнения прямых, на которых лежат стороны ВС и АС;
3) уравнение прямой , на которой лежит высота, проведенная из В;
4) длину этой высоты;
5) уравнение прямой, на которой лежит медиана проведенная из точки А;
6) длину этой медианы;
7) уравнение прямой, на которой лежит биссектриса угла С;
8) центр тяжести треугольника;
9) площадь треугольника;
Ответы к заданиям для самостоятельного решения:
1. 1)63 0 ; 2) 37,9 0 ; 3) 31,3 0 ; 4) 81,2 0 . 2.1)Параллельны;
2)Перпендикулярны; 3)Параллельны; 4)Пересекаются; 5)Пересекаются;
🎬 Видео
Математика без Ху!ни. Уравнение плоскости.Скачать

№976. Найдите координаты точки пересечения прямых 4x + 3y-6 = 0 и 2х+у-4 = 0.Скачать

Решение систем уравнений методом подстановкиСкачать

Точки пересечения графиков линейных функций. 7 класс.ОбразовательныйСкачать

7 класс, 10 урок, Взаимное расположение графиков линейных функцийСкачать

М7 (10.1-10.23) Взаимное расположение прямых.Скачать

9 класс, 7 урок, Уравнение прямойСкачать

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Алгебра 7 класс. Взаимное расположение графиков линейных функцийСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Построить график ЛИНЕЙНОЙ функции и найти:Скачать

9 класс, 8 урок, Взаимное расположение двух окружностейСкачать