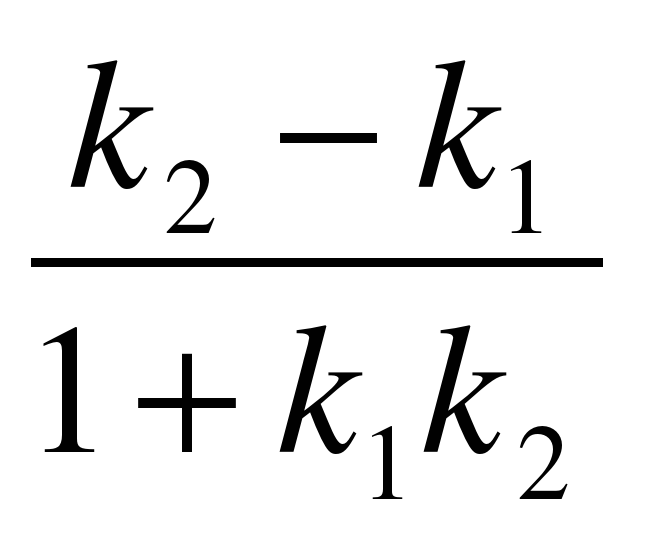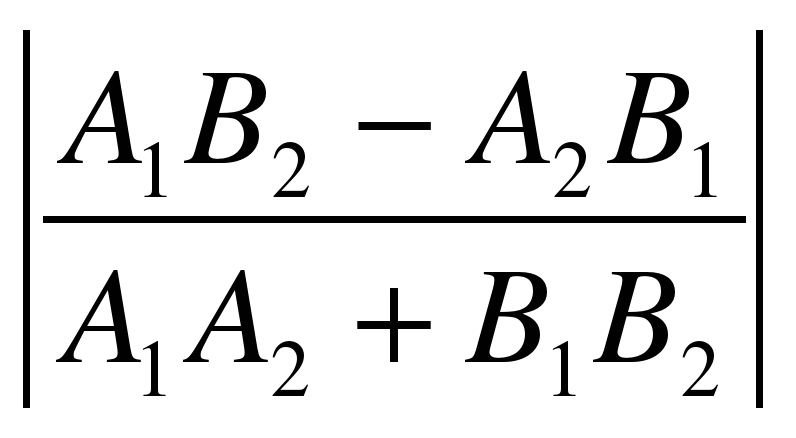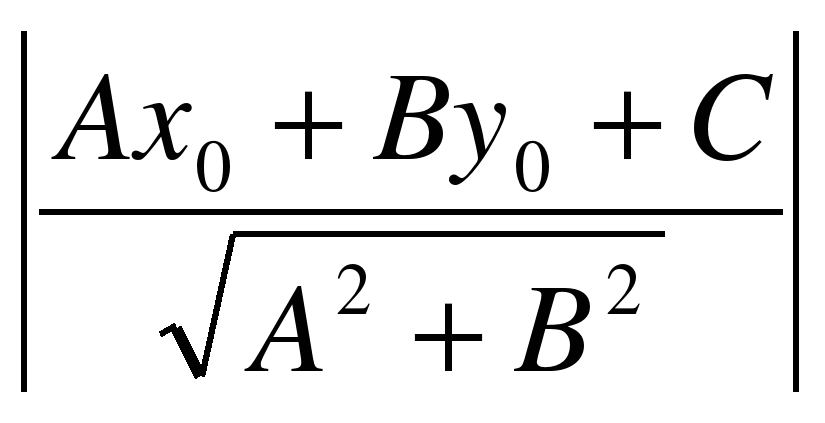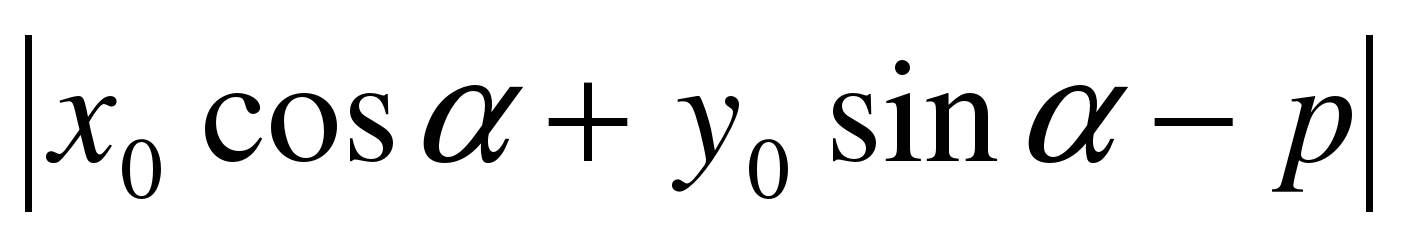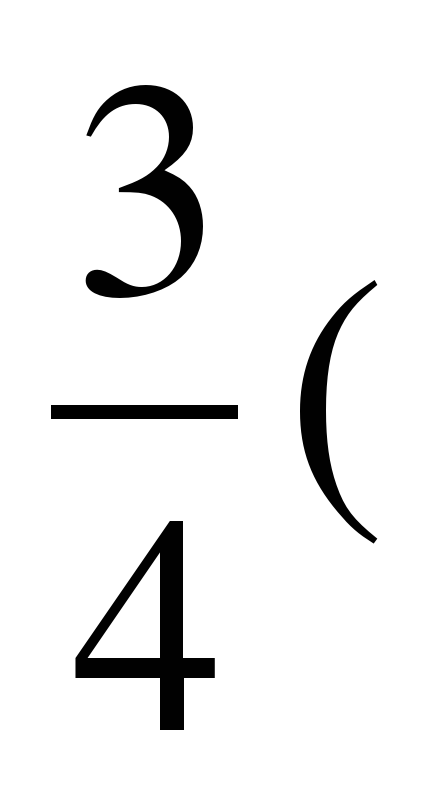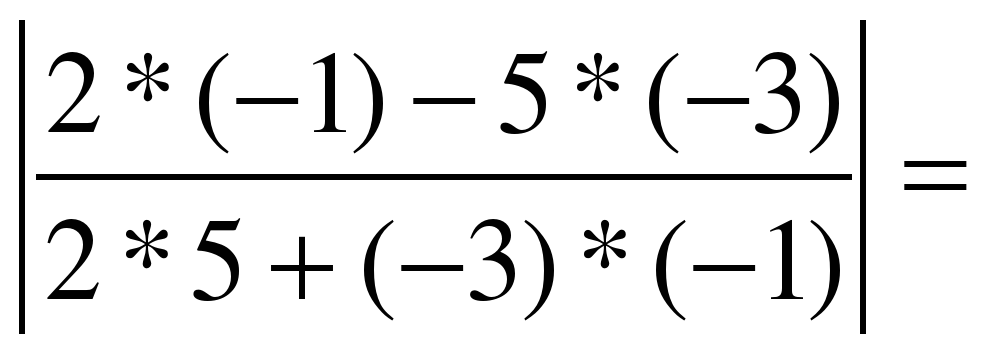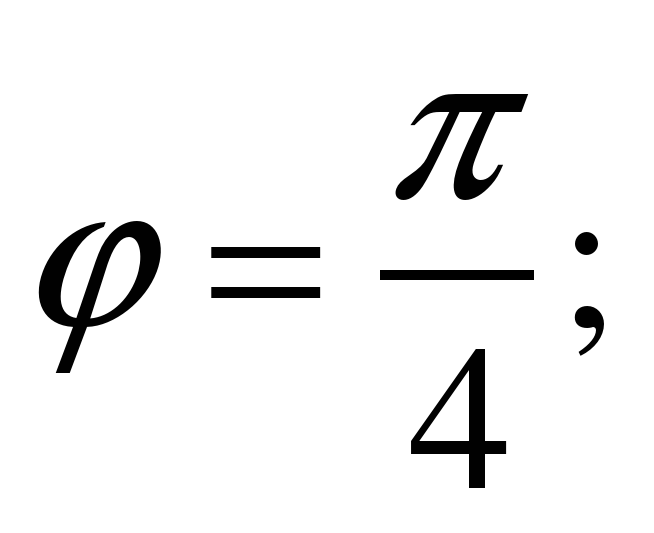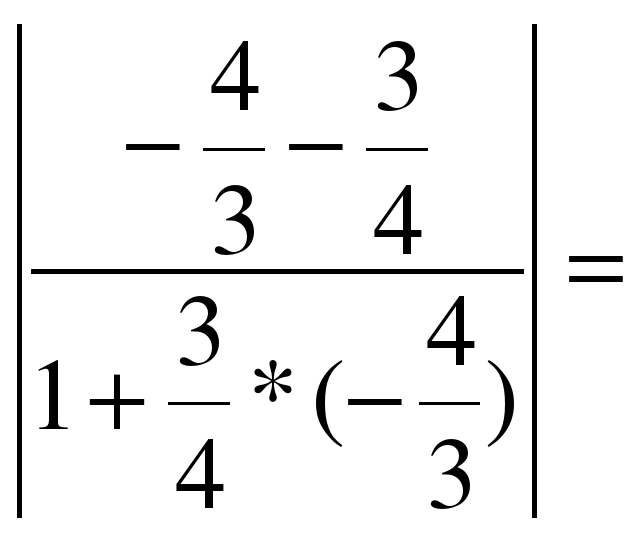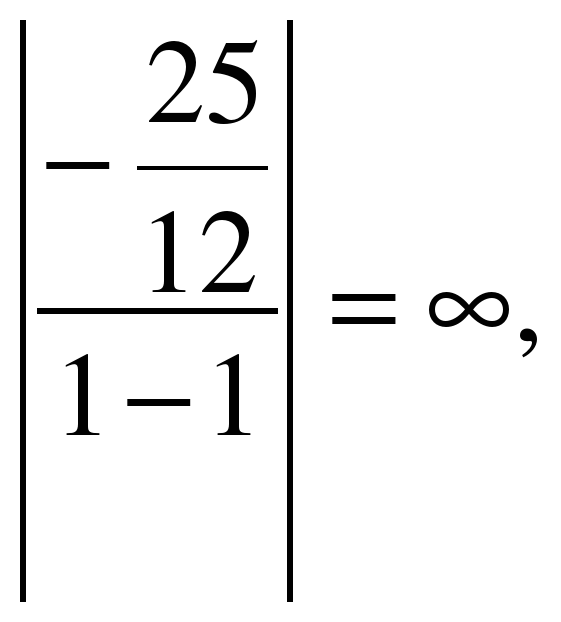Установите взаимное расположение прямых заданных уравнениями 2x 3y 0 и 4x 6y 1 2 (8 видео)

Взаимное расположение плоскостей

Данный калькулятор предназначен для определения взаимного расположения двух плоскостей в пространстве онлайн.

Две плоскости могут иметь три варианта взаимного расположения относительно друг друга. Во-первых, плоскости могут быть параллельны. Во-вторых, они могут быть перпендикулярны. В таком случае угол между плоскостями равен 90 градусам. В-третьих, плоскости могут пересекаться, образовывая при этом два острых и два тупых угла.

Таким образом, с помощью данного калькулятора определяется следующее: пересекаются или нет плоскости, и, если они пересекаются, то перпендикулярны ли они.

Чтобы ответить на вопрос о взаимном расположении плоскостей, необходимо ввести уравнения заданных плоскостей в калькулятор и нажать кнопку «Вычислить».

Содержание

Решение задач по математике онлайн
Калькулятор онлайн. Решение системы двух линейных уравнений с двумя переменными. Метод подстановки и сложения.
Немного теории.
Решение систем линейных уравнений. Способ подстановки
Решение систем линейных уравнений способом сложения
Взаимное расположение прямых
Просмотр содержимого документа «Взаимное расположение прямых»
📹 Видео

Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:№976. Найдите координаты точки пересечения прямых 4x + 3y-6 = 0 и 2х+у-4 = 0.Скачать

Калькулятор онлайн.
Решение системы двух линейных уравнений с двумя переменными.
Метод подстановки и сложения.

С помощью данной математической программы вы можете решить систему двух линейных уравнений с двумя переменными методом подстановки и методом сложения.

Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения двумя способами: методом подстановки и методом сложения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.

При вводе уравнений можно использовать скобки. При этом уравнения сначала упрощаются. Уравнения после упрощений должны быть линейными, т.е. вида ax+by+c=0 с точностью порядка следования элементов.
Например: 6x+1 = 5(x+y)+2

В уравнениях можно использовать не только целые, но также и дробные числа в виде десятичных и обыкновенных дробей.

Правила ввода десятичных дробей.
Целая и дробная часть в десятичных дробях может разделяться как точкой так и запятой.
Например: 2.1n + 3,5m = 55

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &

Примеры.
-1&2/3y + 5/3x = 55
2.1p + 55 = -2/7(3,5p — 2&1/8q)

Решить систему уравнений

Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Немного теории.

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Решение систем линейных уравнений. Способ подстановки

Последовательность действий при решении системы линейных уравнений способом подстановки:
1) выражают из какого-нибудь уравнения системы одну переменную через другую;
2) подставляют в другое уравнение системы вместо этой переменной полученное выражение;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ left< begin 3x+y=7 \ -5x+2y=3 end right. $$

Выразим из первого уравнения y через x: y = 7-3x. Подставив во второе уравнение вместо y выражение 7-Зx, получим систему:
$$ left< begin y = 7—3x \ -5x+2(7-3x)=3 end right. $$

Нетрудно показать, что первая и вторая системы имеют одни и те же решения. Во второй системе второе уравнение содержит только одну переменную. Решим это уравнение:
$$ -5x+2(7-3x)=3 Rightarrow -5x+14-6x=3 Rightarrow -11x=-11 Rightarrow x=1 $$

Подставив в равенство y=7-3x вместо x число 1, найдем соответствующее значение y:
$$ y=7-3 cdot 1 Rightarrow y=4 $$

Пара (1;4) — решение системы

Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными. Системы, не имеющие решений, также считают равносильными.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Решение систем линейных уравнений способом сложения

Рассмотрим еще один способ решения систем линейных уравнений — способ сложения. При решении систем этим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.

Последовательность действий при решении системы линейных уравнений способом сложения:
1) умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;
2) складывают почленно левые и правые части уравнений системы;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.

Пример. Решим систему уравнений:
$$ left< begin 2x+3y=-5 \ x-3y=38 end right. $$

В уравнениях этой системы коэффициенты при y являются противоположными числами. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной 3x=33. Заменим одно из уравнений системы, например первое, уравнением 3x=33. Получим систему
$$ left< begin 3x=33 \ x-3y=38 end right. $$

Из уравнения 3x=33 находим, что x=11. Подставив это значение x в уравнение ( x-3y=38 ) получим уравнение с переменной y: ( 11-3y=38 ). Решим это уравнение:
( -3y=27 Rightarrow y=-9 )

Таким образом мы нашли решение системмы уравнений способом сложения: ( x=11; y=-9 ) или ( (11; -9) )

Воспользовавшись тем, что в уравнениях системы коэффициенты при y являются противоположными числами, мы свели ее решение к решению равносильной системы (сумировав обе части каждого из уравнений исходной симтемы), в которой одно из уравнений содержит только одну переменную.

Видео:Взаимное расположение прямых на плоскости. 7 класс.Скачать

Взаимное расположение прямых

Угол между двумя прямыми, условия параллельности и перпендикулярности двух прямых, пересечение прямых, расстояние от данной точки до данной прямой.

Просмотр содержимого документа
«Взаимное расположение прямых»

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ.

Под углом между прямыми в плоскости понимают меньший (острый) из двух смежных углов образованными этими прямыми.

Если прямые l₁ и l₂ заданы уравнениями с угловыми коэффициентами у=к₁х+b₁ и у=к₂х+b_2, то угол φ между ними вычисляется по формуле

tg φ=

Условие параллельности прямых l₁ и l₂ имеет вид

а условие их перпендикулярности

k₁ = — 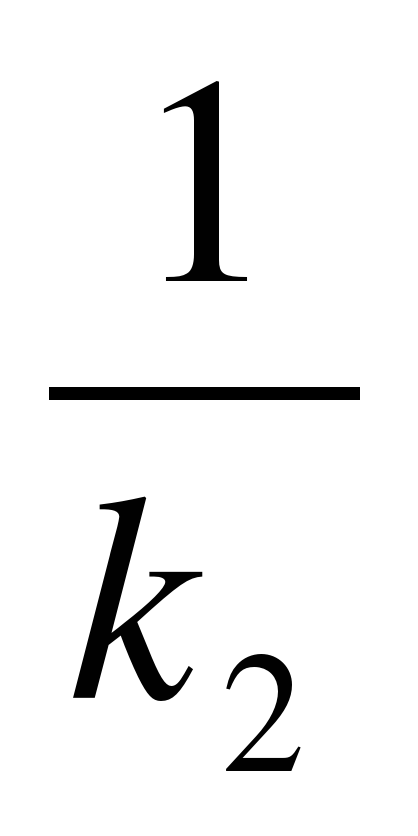(или k₁k₂= — 1)

то величина φ угла между ними вычисляется по формуле

tg φ=

угловые их параллельности

( или А₁В₂-А₂В₁=0)

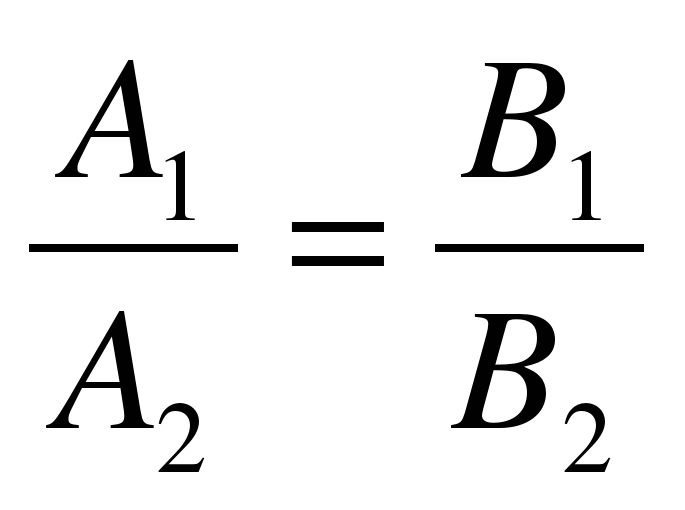
Условие их перпендикулярности

Для нахождения общих точек прямых l₁ и l₂ необходимо решить систему

уравнений

А₁х+В₁у+С₁=0, у=k₁x+b₁

или

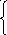
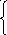
Если 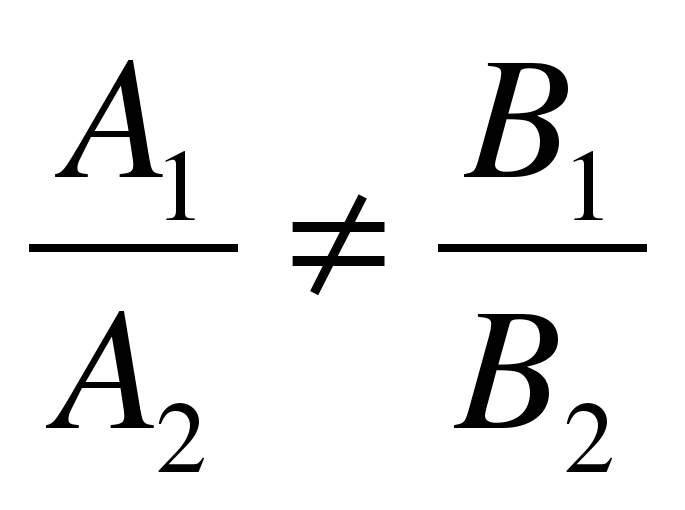, то имеется единственная точка пересечения прямых ;

Если 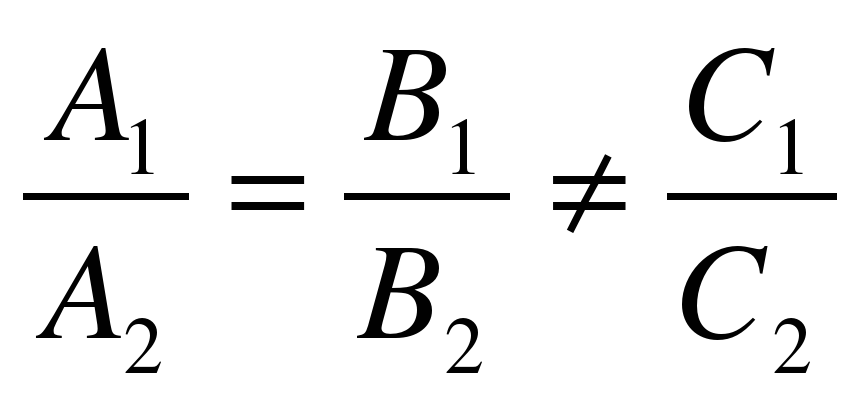— прямые l₁ и l₂ не имеет общей точки, т. е параллельны;

Если 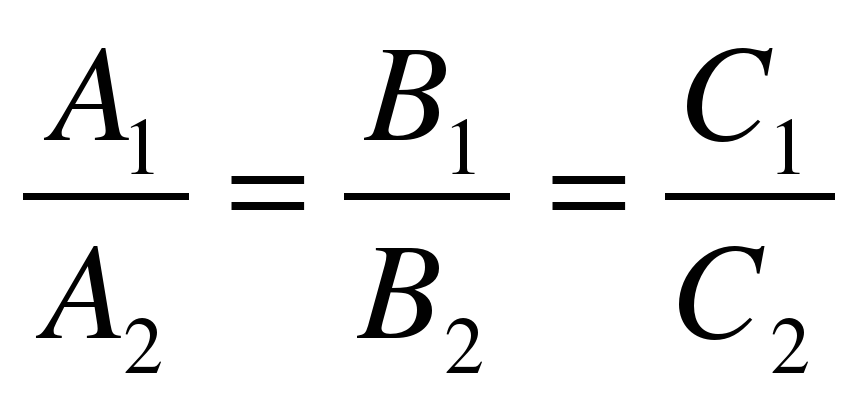-прямые имеют бесконечное множество точек т.е совпадают

Расстоянием d от точки М₀ (х₀;у₀) до прямой Ах+Ву+С=0 называется длина перпендикуляра , опущенного из этой точки на прямую .

Расстояние d определяется по формуле

Расстояние от точки М₀ (х₀;у₀) до прямой х cos + y sin— p=0 вычисляется по формуле

ПРИМЕР: найти угол между прямыми :

1) y=2x-3 и y=;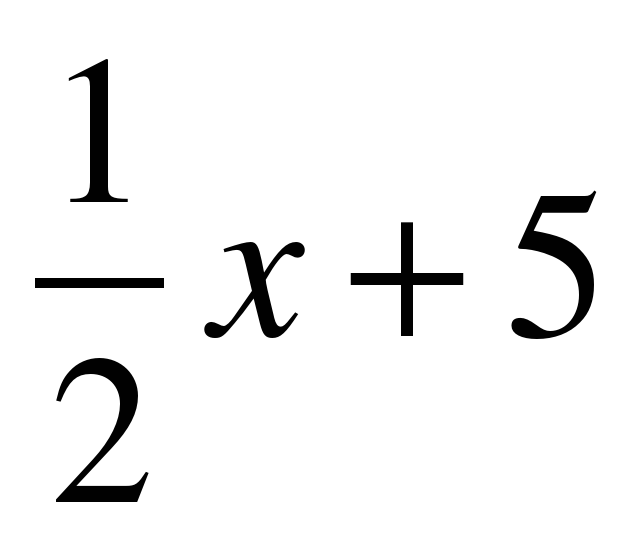

2) 2x-3y+10=0 и 5x – y+4=0;

3) y= 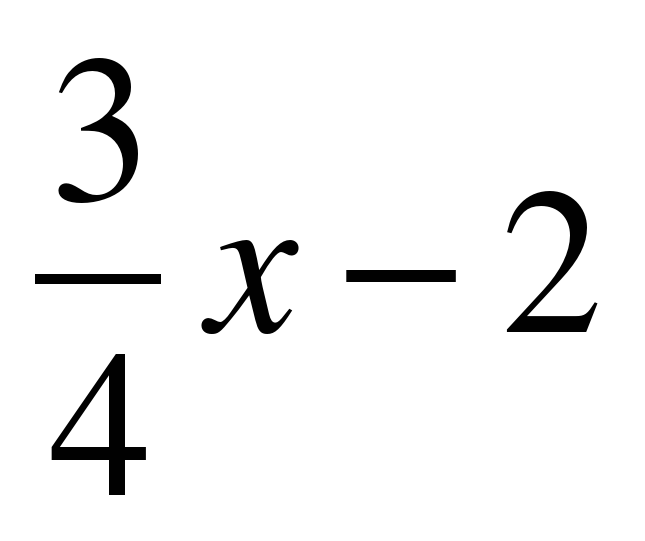и 8x+6y+5=0;

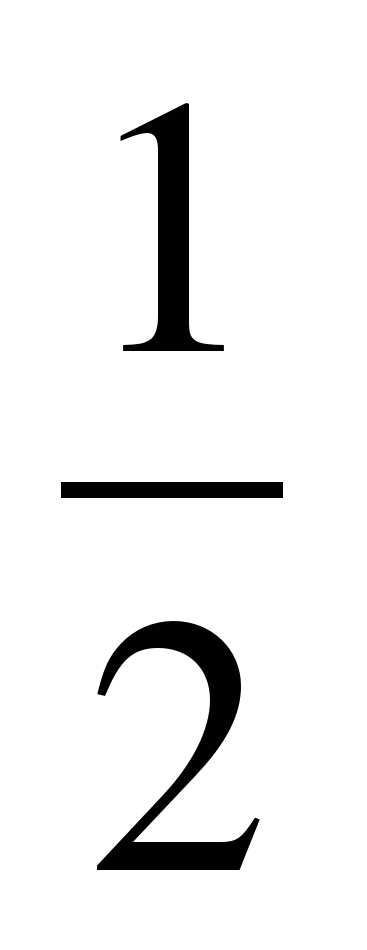
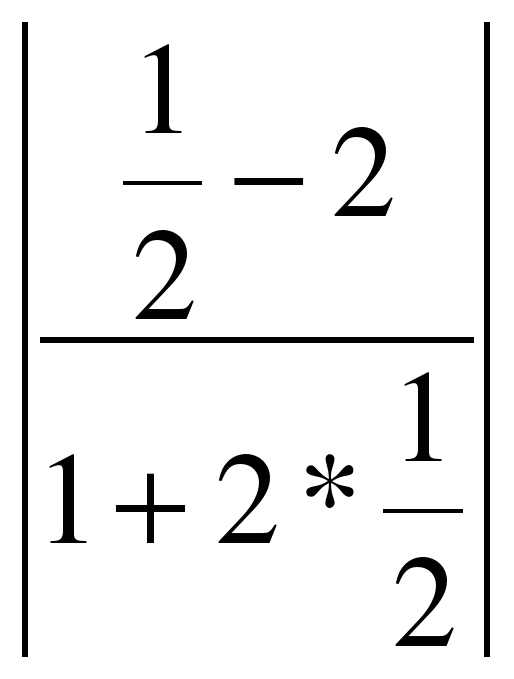
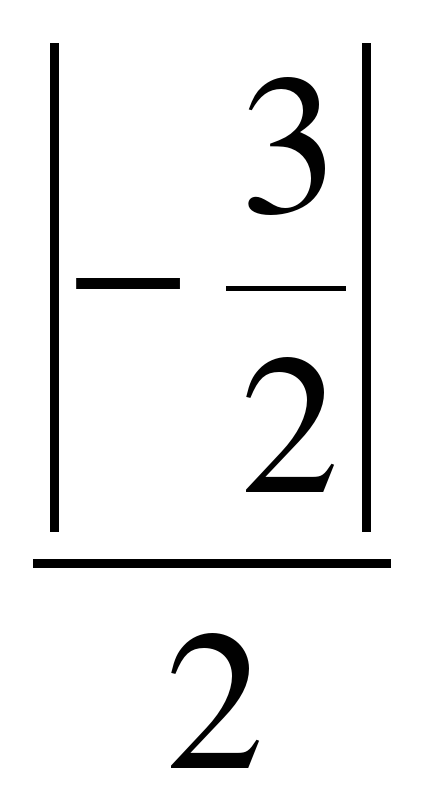
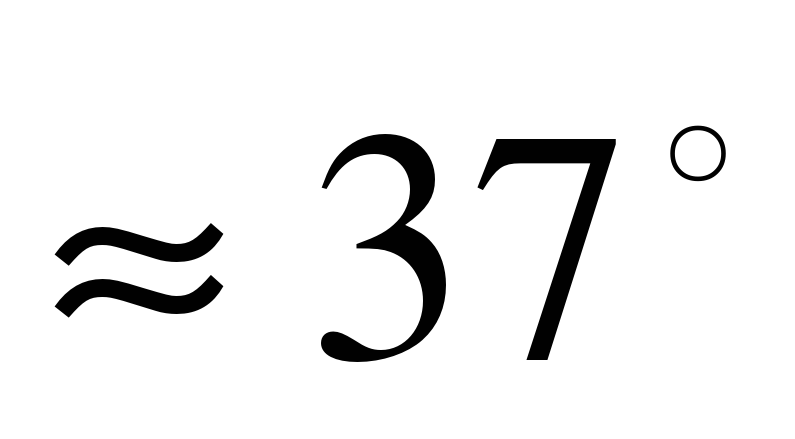
Воспользуемся формулой. Подставляя в неё значения k₁=2 и k₂= , находим tg===

=arctg);

Подставим значения А₁ = 2, В₁=-3,А₂=5,В₂=-1 в формулу : tg==1,

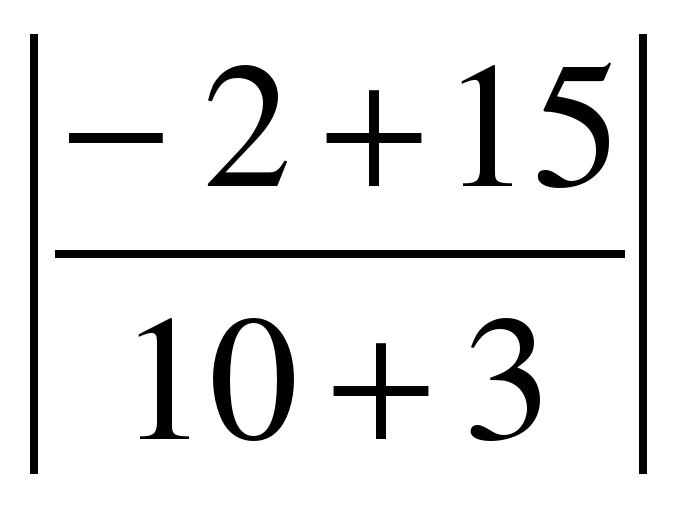
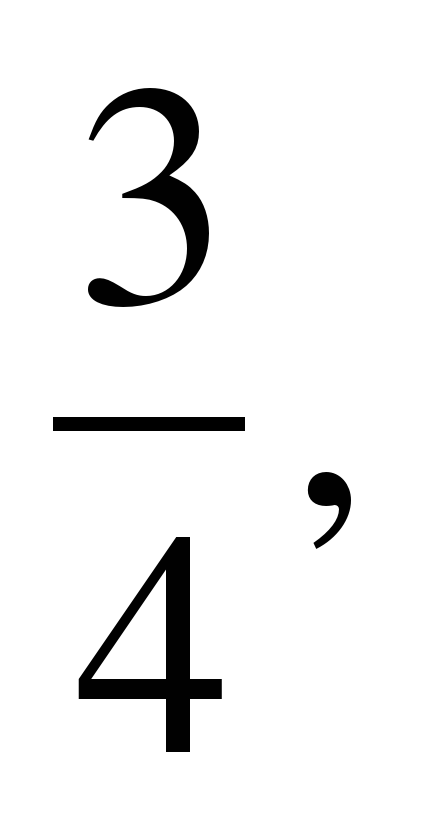
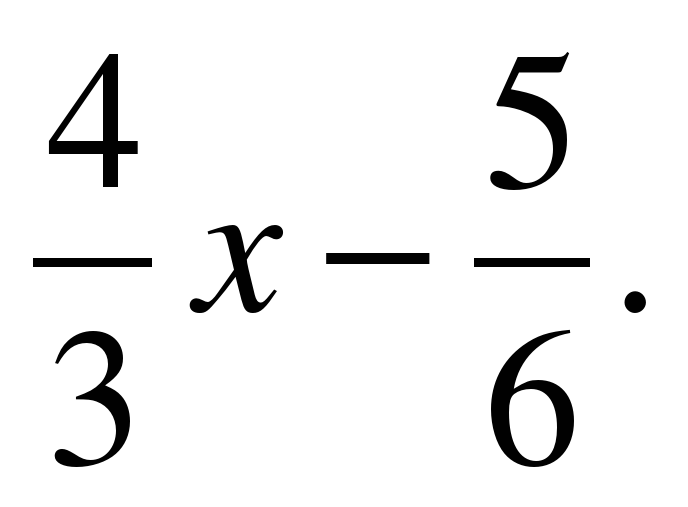
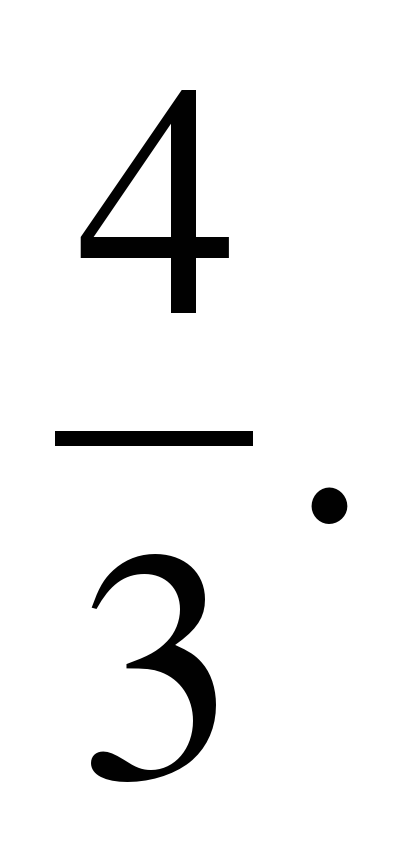
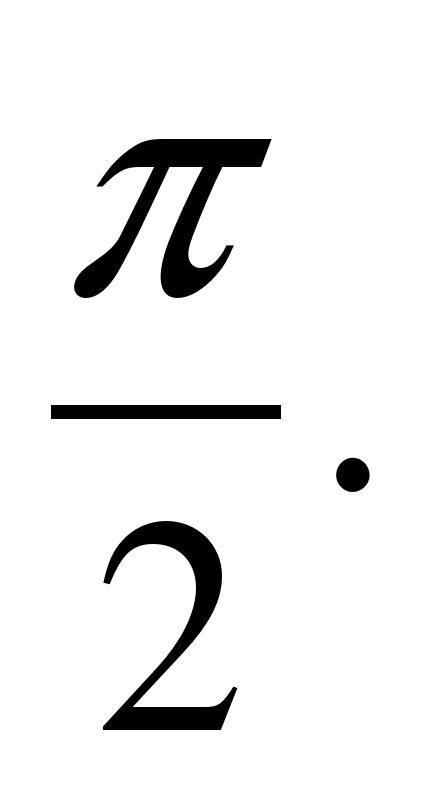
Здесь k₁=найдём k₂. Для этого перейдём от 6y =-8x-5 к эквивалентному равенству y=- Здесь k₂=-Так как k₁*k₂=-1, то данные прямые перпендикулярны. (По формуле получаем:tg==)

k₁=5,k₂=5, tg=0,=0.

Задания для практических занятий:

1. Найти угол между прямыми:

2) 2х-3у-7=0 и 2х-у+5=0;

3) у=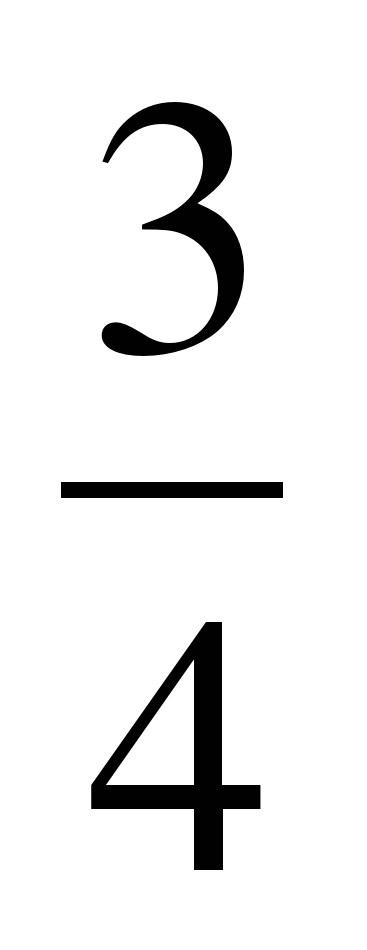х+6 и 3х-2у-8=0;

4) у= 7х -1 и у=7х+1;

2. Исследовать взаимное расположение следующих пар прямых:

1) 3х+5у-9=0 и 10х-6у+4=0

2) 2х+5у-2=0 и х+у+4=0;

3) 2у=х-1 и 4у-2х+2=0;

5) =1 и у=х+2;

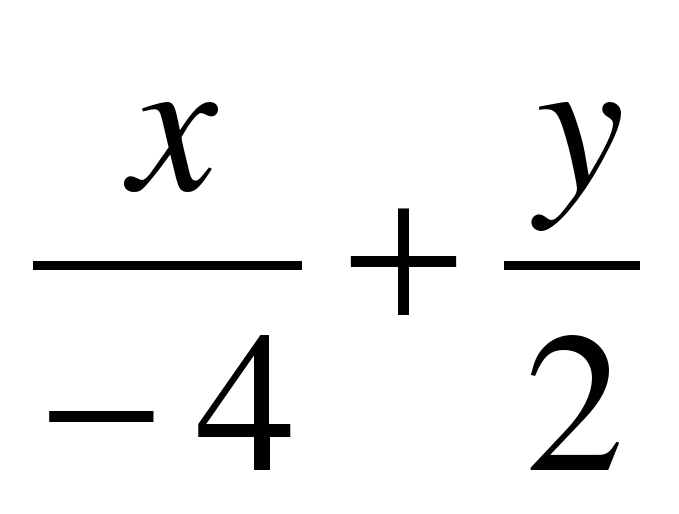
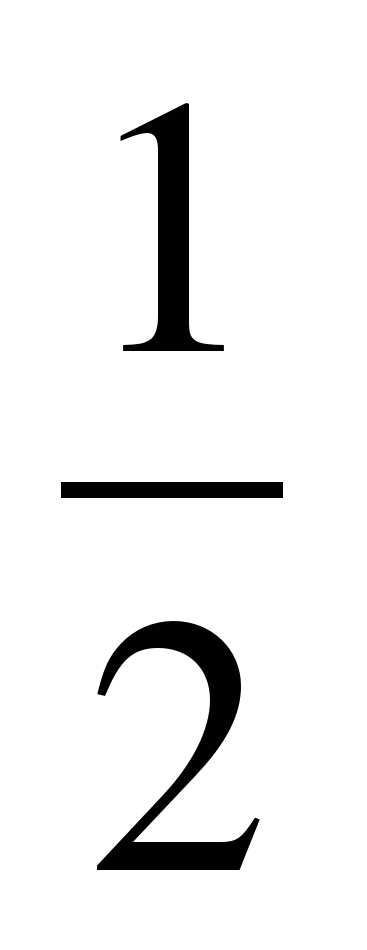
8) у=3-6х и 12х+2у-5=0;

10) х —у-1=0 и х +у+2=0

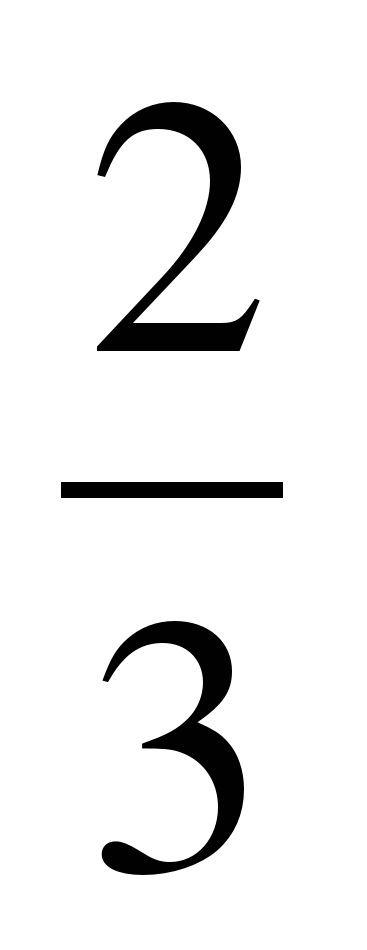
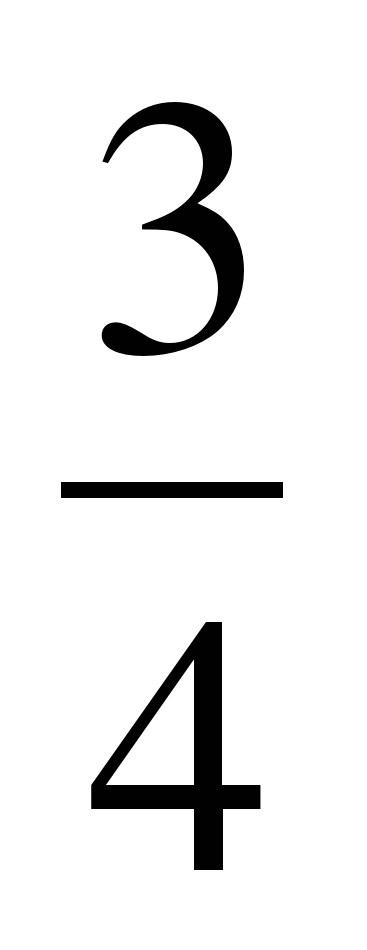
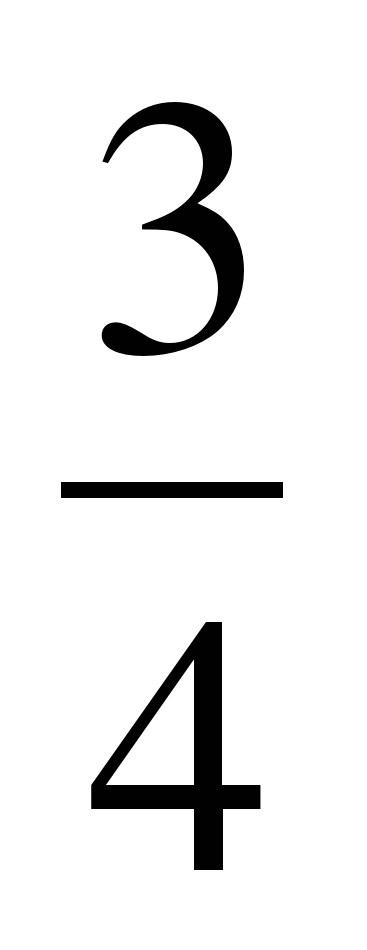
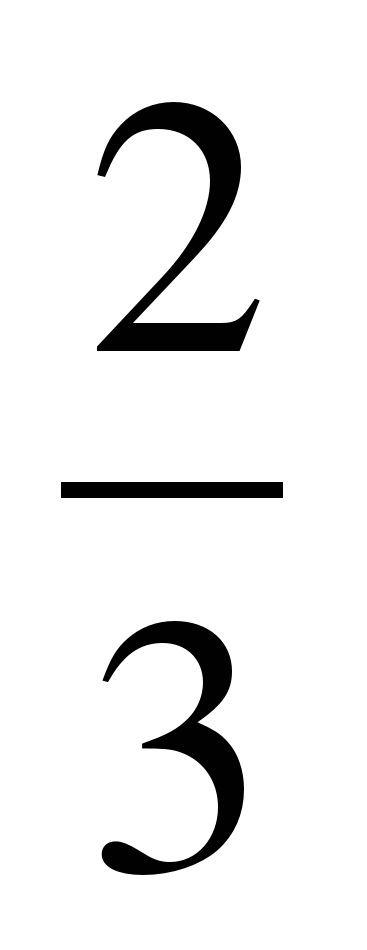
3. При каких значениях следующие пары прямых: а) параллельны; б) перпендикулярны.

1) 2х-3у+4=0 и х-6у+7=0;

2) х-4у+1=0 и -2х+у+2=0;

3) 4х+у-6=0 и 3х+у-2=0;

4) х- у+5=0 и 2х+3у+3=0;

4.Через точку пересечения прямых 3х-2у+5=0; х+2у-9=0 проведена прямая, параллельная прямой 2х+у+6=0. Составить ее уравнение.

5. Найти уравнение прямой, проходящий через точку А (-1;2):

а) параллельно прямой у=2х-7;

б) перпендикулярно прямой х+3у-2=0.

6. Найти длину высоты ВД в треугольнике с вершинами А (4;-3); В (-2;6) и С (5;4).

7. Даны уравнения сторон треугольника: х+3у-3=0, 3х-11у-29=0 и 3х-у+11=0.

Найти вершины этого треугольника.

Задания для самостоятельного решения

1. Найти острый угол между прямыми:

2) 2х-3у+6=0 и 3х-у-3=0

4) 3х+4у-12=0 и 15х-8у-45=0

2. Исследовать взаимное расположение следующих пар прямых:

1) 2х-3у+4=0 и 10х+3у-6=0

2) 3х-4у+12=0 и 4х+3у-6=0

3) 25х+20у-8=0 и 5х+4у+4=0

4) 4х+5у-8=0 и 3х-2у+4=0

3. Найти уравнение прямой, проходящий через точку В (2;-3)

а) параллельно прямой, соединяющей точки М₁ (-4;0) и М₂ (2;2);

б) перпендикулярно прямой х-у=0.

4. Составить уравнение прямой, содержащий высоту ВД в треугольнике с вершинами

А (-3;2), В (5;-2), С (0; 4)

5. Найти площадь треугольника, образованного прямыми 2х+у+4=0, х+7у-11=0 и 3х-5у-7=0.

6.Через точку пересечения прямых 3х+2у-4=0 и х-5у+8=0 проведены прямые, одна из которых проходит через начало координат, а другая параллельна оси Ох. Составить их уравнения.

7. Дан четырехугольник АВСД с вершинами А (3;5); В (6;6); С (5;3); Д (1;1). Найти:

а) координаты точки пересечения диагоналей;

б) угол между диагоналями.

8.Даны вершины треугольника А(2;-2), В (3;5), С (6;1). Найти:

1) длины сторон АС и ВС;

2) уравнения прямых, на которых лежат стороны ВС и АС;

3) уравнение прямой , на которой лежит высота, проведенная из В;

4) длину этой высоты;

5) уравнение прямой, на которой лежит медиана проведенная из точки А;

6) длину этой медианы;

7) уравнение прямой, на которой лежит биссектриса угла С;

8) центр тяжести треугольника;