Все электромагнитные процессы макроскопической электродинамики подчиняются уравнениям Максвелла, сформулированным в 1873 г. в виде дифференциальных уравнений. Эти уравнения связывают воедино электрические и магнитные характеристики поля:
rot H = Iпр + 

rot Е = — 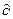

div D = 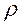
Физический смысл этих уравнений заключается в следующем.
Первое уравнение Максвелла(5.9,а) является обобщенным законом Ампера (закон полного тока) и говорит о том, что если в некоторой точке пространства существует переменное электрическое поле Е, создающее токи проводимости Iпр = σE и токи смещения Iсм = iω 
Второе уравнение Максвелла (5.9,б) является обобщенным законом магнитной индукции Фарадея. Фарадей установил, что если замкнутый контур пронизывается переменным магнитным потоком Ф, то в контуре возникает электродвижущая сила (ЭДС) равная скорости изменения магнитного потока:
е = — 

Знак «минус» в правой части означает, что возникающая в контуре ЭДС стремится воспрепятствовать изменению потока, пронизывающего контур.
Физический смысл второго уравнения Максвелла заключается в том, что всякое изменение магнитного поля во времени непрерывно вызывает независимо от параметров среды появление электрического поля.
Второе уравнение Максвелла связано с гармоническим колебанием соотношением:
rot Е = — 

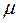
т.е. оно утверждает, что если в некоторой точке пространства существует переменное магнитное поле, то в окрестностях этой точки возникает переменное вихревое электрическое поле. Магнитное поле и создаваемое им электрическое поле образуют левовинтовую систему.
Следует отметить, что электрическое поле может быть как вихревым, так и потенциальным. Источником потенциального электрического поля являются заряды (в случае электрических полей), которые находятся в тех точках пространства, где текут токи проводимости, представляющие собой движущиеся заряды.
Таким образом, гармоническое электрическое поле может быть вихревым, потенциальным или представлять суперпозицию (сумму) потенциального и вихревого полей, тогда как магнитное поле только вихревое.
Первое и второе уравнения Максвелла говорят о том, что между электрической и магнитной составляющими в переменном электромагнитном поле существует тесная взаимосвязь, которая выражается тем, что созданное сторонними источниками меняющееся во времени электромагнитное поле, может существовать вне этого источника за счет собственной энергии, перекачивающейся из энергии электрического поля в энергию магнитного поля и обратно.
Третье уравнение Максвелла(материальное уравнение 5.9,в) — это обобщенный закон Гаусса для случая переменных процессов, физически означает, что источником электрического поля являются электрические заряды, т.е. электрическая индукция D связана с плотностью электрических зарядов 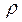
Четвертое уравнениеМаксвелла (материальное уравнение 5.9,г) показывает, что в природе отсутствуют магнитные заряды, а линии вектора В непрерывны и всегда пронизывают любую замкнутую поверхность.
Таким образом, третье и четвертое уравнения Максвелла учитывают электрическую и магнитную характеристики среды. Действительно, в случае линейных изотропных сред можно записать:
D = 
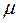
Следует отметить, что к основным уравнениям электродинамики относят и закон Ома в дифференциальной форме (5.6), который выражает зависимость плотности тока Iпр в какой-либо точке проводящей сферы от напряженности электрического поля в этой точке.
Таким образом, мы рассмотрели основные уравнения электродинамики, каждое из которых описывает те или иные свойства электромагнитного поля. Однако, для полного анализа электродинамических процессов необходимо использовать полную систему уравнений Максвелла, содержащую основные уравнения Максвелла (5.9,а-г) и материальные уравнения (5.6) и (5.10), которая записывается в виде:
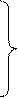



rot Е = — 

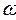
div D = 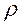
D = 
Поскольку уравнения (5.13) и (5.14) являются линейными дифференциальными уравнениями, можно утверждать, что электромагнитные поля удовлетворяют принципу суперпозиции.
Видео:ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений МаксвеллаСкачать

ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
Читайте также:
|
Установите соответствие между уравнениями Максвелла и их физическим смыслом. 1.  2. 2.  3. 3.  |
Укажите соответствие для каждого нумерованного элемента задания
1.Изменяющееся со временем магнитное поле порождает вихревое электрическое поле.
2. Источником вихревого магнитного поля помимо токов проводимости является изменяющееся со временем электрическое поле.
3. «Магнитных зарядов» не существует: силовые линии магнитного поля замкнуты.
Каждый из четырех одинаковых по модулю точечных зарядов (см. рис.), расположенных в вершинах квадрата, создает в точке пересечения диагоналей электрическое поле, напряженность которого равна 

Градиент потенциала поля в этой точке равен _______и направлен горизонтально …

На рисунке показана зависимость силы тока в электрической цепи от времени.

Заряд, прошедший по проводнику в интервале времени от 0 до 10 
На рисунке изображены сечения двух прямолинейных длинных параллельных проводников с одинаково направленными токами, причем 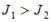

Если магнитный поток сквозь катушку из 20 витков изменяется по закону 

Уравнения Максвелла являются основными законами классической макроскопической электродинамики, сформулированными на основе обобщения важнейших законов электростатики и электромагнетизма. Эти уравнения в интегральной форме имеют вид:
1) 
2) 
3) 
4) 
Первое уравнение Максвелла является обобщением …
закона электромагнитной индукции
Установите соответствие между величиной (знаком) работы сил электростатического поля, создаваемого зарядом +Q, по перемещению отрицательного заряда –q и траекторией перемещения (указаны начальная и конечная точки).

1. А=0
2. А
Если магнитный поток сквозь катушку из 20 витков изменяется по закону 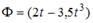

Одно из уравнений Максвелла представляет собой обобщение закона полного тока для поля в веществе и математически может быть выражено уравнениями …
Удельное сопротивление проводника из стали 

Магнитный момент 

случае …
По параллельным металлическим проводникам, расположенным в однородном магнитном поле, с равномерно возрастающей скоростью перемещается проводящая перемычка (см. рис.). Если сопротивлением перемычки и направляющих можно пренебречь, то зависимость индукционного тока от времени можно представить графиком …
Уравнения Максвелла являются основными законами классической макроскопической электродинамики, сформулированными на основе обобщения важнейших законов электростатики и электромагнетизма. Эти уравнения в интегральной форме имеют вид:
1) 
2) 
3) 
4) 
Второе уравнение Максвелла является обобщением …
закона полного тока в среде
К источнику тока с внутренним сопротивлением 1,0 Ом подключили реостат. На рисунке показан график зависимости силы тока в реостате от его сопротивления.

Максимальная мощность, которая выделяется в реостате, равна …
Прямоугольная проводящая рамка расположена в одной плоскости с прямолинейным проводником, по которому течет ток I (рис.). В рамке возникает индукционный ток при …
— вращении рамки вокруг оси, совпадающей со стороной LM рамки
— вращении рамки вокруг оси, совпадающей со стороной KL рамки
— поступательном перемещении рамки вдоль оси ОХ
Вещество является однородным изотропным парамагнетиком, если магнитная восприимчивость …
мала, вектор намагниченности направлен в ту же сторону, что и вектор напряженности внешнего магнитного поля
Установите соответствие между источником электростатического поля и формулой, позволяющей вычислить напряженность поля в некоторой точке.
1. Точечный заряд
2. Равномерно заряженная длинная нить
3. Равномерно заряженная бесконечная плоскость
1
2
3
Удельное сопротивление проводника из стали 

Для электронной поляризации диэлектриков характерно …
возникновение у молекул индуцированного дипольного момента при помещении диэлектрика во внешнее электрическое поле

Укажите верные утверждения.
— Вектор магнитной индукции 
— Кинетическая энергия электрона остается постоянной.
— Вектор силы Лоренца, действующей на электрон, направлен для указанного на рисунке положения электрона вправо.
Уравнения Максвелла являются основными законами классической макроскопической электродинамики, сформулированными на основе обобщения важнейших законов электростатики и электромагнетизма. Эти уравнения в интегральной форме имеют вид:
1) 
2) 
3) 
4) 
Первое уравнение Максвелла является обобщением …
закона электромагнитной индукции
Сила тока в проводящем круговом контуре индуктивностью 100 мГн изменяется с течением временипо закону 

Абсолютная величина ЭДС самоиндукции равна____ ; при этом индукционный ток направлен …
0,03 В; против часовой стрелки
Дата добавления: 2015-02-16 ; просмотров: 343 | Нарушение авторских прав
Видео:Билеты №32, 33 "Уравнения Максвелла"Скачать

Уравнения Максвелла, их физический смысл
Созданная Максвеллом единая макроскопическая теория электромагнитного поля позволила с единой точки зрения не только объяснить электрические и магнитные явления, но предсказать новые, существование которых было впоследствии подтверждено на практике (например, открытие электромагнитных волн).
Итак, переменное магнитное поле вызывает появление вихревого электрического поля. Переменное электрическое поле вызывает появление магнитного поля. Взаимно порождаясь, они могут существовать независимо от источников заряда или токов, которые первоначально создали одно из них. В сумме это есть электромагнитное поле (ЭМП). Превращение одного поля в другое и распространение в пространстве есть способ существования ЭМП. Конкретные проявления ЭМП — радиоволны, свет, гамма-лучи и т.д.
Теорию ЭМП Максвелл сформулировал в виде системы нескольких уравнений. В учении об электромагнетизме эти уравнения Максвелла играют такую же роль, как уравнения (или законы) Ньютона в механике.
Обобщая рассмотренные выше положения, приведем уравнения, составляющие основу электромагнитной теории Максвелла.
1) Первое уравнение — теорема о циркуляции вектора напряженности магнитного поля:
Это уравнение является обобщением закона Био-Савара-Лапласа и показывает, что циркуляция вектора напряженности н магнитного поля по произвольному замкнутому контуру L равна сумме токов проводимости и токов смещения сквозь поверхность, натянутую на этот контур. Или другими словами, показывает связь между полным током и порождаемым им магнитным полем, то есть магнитные поля могут создаваться либо движущимися зарядами (токами проводимости), либо переменными электрическими полями.
В дифференциальной форме это уравнение Максвелла выглядит так:
где вектор j — обозначает плотность протекающих сквозь проводник реальных токов проводимости, а производная вектора поляризации D по времени (dD/dt) называется током смещения jCM, т.е. вектор тока состоит из двух составляющих: j„p + jCM.
Математическая операция rot Н (ротор) означает, что магнитное поле вокруг проводников с током имеет вихревой характер, то есть его силовые линии имеют вид колец, «надетых» на вектор, показывающий направление тока. Причем rot Я отличен от нуля только для вихревого поля с кольцеобразными замкнутыми силовыми линиями.
Здесь уместно сказать, что первое уравнение дает прекрасный критерий для различения диэлектриков и проводников. Если в среде токи проводимости больше токов смещения, то среда — проводник, если меньше, то диэлектрик. Идеальный диэлектрик — вакуум, в котором токи проводимости вообще отсутствуют. Колебания тока проводимости синфазны с колебаниями электрического поля, поэтому токи проводимости вызывают выделение энергии в среде с проводимостью, что приводит к тепловым потерям и уменьшению энергии электромагнитного поля.
Итак, первое уравнение Максвелла утверждает, что изменения электрического поля порождают вихревое магнитное поле.
2) Второе уравнение (закон Фарадея) циркуляция вектора напряженности суммарного электрического поля равна:
Это уравнение описывает явление электромагнитной индукции и устанавливает количественную связь между электрическими и магнитными полями: переменное магнитное поле порождает переменное электрическое поле, а источниками электрического поля могут быть как электрические заряды, так и меняющиеся во времени магнитные поля.
В дифференциальной форме это уравнение выглядит так:
Это означает, что ЭДС в любом замкнутом контуре равна скорости изменения (т.е. производной по времени) магнитного потока или то, что вихревое электрическое поле порождается изменениями магнитного поля.
3) Третье уравнение выражает теорему Остроградского-Гаусса для статистических электрических и магнитных полей
т.е. поток вектора электрической индукции D в диэлектрике через замкнутую поверхность S равен сумме зарядов с объемной плотностью р внутри этой поверхности. Это уравнение показывает также, что силовые линии вектора электрической индукции D и напряженности электрического поля Е начинаются и заканчиваются на зарядах.
В дифференциальной форме
т.е. дивергенция (или извержение) вектора электрической индукции D равна плотности заряда р, следовательно, источником электростатического поля является электрический заряд.
4) Четвертое уравнение выражает теорему Остроградского- Гаусса для переменного магнитного поля
Это уравнение показывает то свойство магнитного поля, что линии вектора магнитной индукции В всегда замкнуты. Оно утверждает, что магнитных зарядов в природе не существует, поэтому в дифференциальной форме уравнение имеет вид:
означающий, что нет извержения вектора магнитной индукции в.
Уравнения (3.79) — (3.86) составляют полную систему уравнений Максвелла. Они являются наиболее общими для электрических и магнитных полей в покоящихся средах. Физический смысл уравнений Максвелла в дифференциальной и интегральной формах полностью эквивалентен.
Однако для полного описания явлений в электрических и магнитных полях к уравнениям Максвелла надо добавить уравнения состояния или материальные уравнения. Вид этих уравнений определяется электрическими и магнитными свойствами среды:
здесь о — удельная проводимость, )стр — плотность сторонних токов.
Эти материальные уравнения показывают, что между величинами, входящими в уравнения Максвелла, существует взаимосвязь: а именно вектор электрической индукции D связан с вектором напряженности электрического поля Е, а вектор магнитной индукции В связан с вектором
напряженности магнитного поля Н через значения электрической и магнитной постоянных и значения диэлектрической и магнитной проницаемости среды соответственно. И, наконец, вектор полного тока состоит из двух составляющих: тока проводимости и тока сторонних сил.
Очевидно, что уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.
Для стационарных полей (Е=const, Z?=const) уравнения Максвелла принимают вид:
т.е. источниками магнитного поля в данном случае являются только токи проводимости, а источниками электрического поля — только электрические заряды. В этом частном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрические и магнитные поля.
Таким образом, уравнения Максвелла — наиболее общие уравнения для электрических и магнитных полей в покоящихся средах.
На уравнениях Максвелла основана целая наука — электродинамика, позволяющая строгими математическими методами решить множество полезных практических задач, например, рассчитать поле излучения различных антенн, как в свободном пространстве, так и вблизи поверхности Земли или около корпуса какого-либо летательного аппарата, конструкцию антенн, волноводов и объемных резонаторов.
💡 Видео
О чем говорят уравнения Максвелла? Видео 1/2Скачать

Вывод уравнений МаксвеллаСкачать

Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

3 14 Уравнения МаксвеллаСкачать

Уравнения Максвелла и соответствующие уравнения Волновой МоделиСкачать

Уравнения Максвелла 2021Скачать

Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

Григорий Перельман 08.06.2017Скачать

Лекция №9. Уравнения МаксвеллаСкачать

Лекция №14 "Электричество и магнетизм" (Попов П.В.): Уравнения МаксвеллаСкачать

Почему скорость света 299 792 458 метров в секунду?Скачать

3 Уравнения Максвелла в дифференциальной формеСкачать

Электромагнитные волны и уравнения Максвелла — Эмиль АхмедовСкачать

Дональд Хоффман: Реальность - это иллюзия - Как эволюция скрыла правду | на русском #293Скачать

Уравнения Максвелла — Мартин МакколлСкачать

Уравнения Максвелла Лекция 10-1Скачать

Джеймс Клерк Максвелл. Научные труды и вклад в наукуСкачать

Электродинамика | уравнения Максвелла | 1 | для взрослыхСкачать
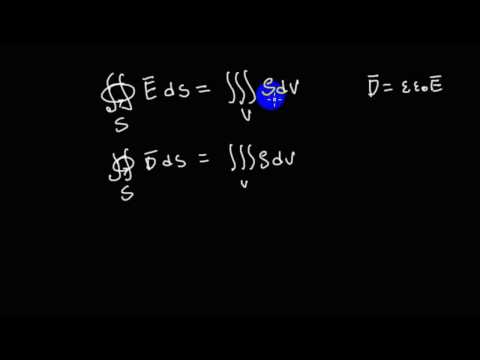
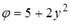 . Вектор напряженности электрического поля в точке А будет иметь направление, показанное стрелкой …
. Вектор напряженности электрического поля в точке А будет иметь направление, показанное стрелкой …

 мВб, то ЭДС индукции, возникающая в катушке в момент времени
мВб, то ЭДС индукции, возникающая в катушке в момент времени 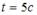 , равна …(ответ выразите в В и округлите до целых)
, равна …(ответ выразите в В и округлите до целых) ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
, 
 , то циркуляция вектора напряженности магнитного поля по контуру
, то циркуляция вектора напряженности магнитного поля по контуру  равна …
равна …




















