Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
- Тест по темам «Уравнение», «Некоторые методы решения уравнений», «Графическое решение уравнений»
- Вариант 1
- Решения к заданиям для варианта 1
- Тест по темам «Уравнение», «Некоторые методы решения уравнений», «Графическое решение уравнений»
- Вариант 2
- Решения к заданиям для варианта 2
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Урок алгебры в 8-м классе по теме «Графический способ решения уравнений»
- Задания ОГЭ на анализ графиков Начало
- Изученные функции и их графики.
- Задания на соответствие графика и формулы функции.
- Линейная функция. Прямая линия.
- 📺 Видео
Видео:[ОГЭ] Установите соответствие между графиками функций и формулами, которые их задаютСкачать
![[ОГЭ] Установите соответствие между графиками функций и формулами, которые их задают](https://i.ytimg.com/vi/TI55U5oNiyc/0.jpg)
Тест по темам «Уравнение», «Некоторые методы решения уравнений», «Графическое решение уравнений»
Вариант 1
Решите систему уравнений

графически и введите ответ.
Ответ:
x = __; y = _.
Постройте график функции 

Постройте график линейной функции 


А)
Б)
В)
Г)
Выберите уравнения, соответствующие данным графическим изображениям.
1) 

Решите уравнение и запишите его корень.
Допишите решение уравнения.
2,31x + 0,58x = 13,48 – 1,92
Приведем подобные слагаемые:
____x = _____
Запишем формулу для корня:
x = _____ : ____
Вычислим и запишем корень:
x = _
Известно, что ордината некоторой точки прямой, являющейся графиком уравнения 

Ответ: абсцисса этой точки – __.
Решите задачу, использовав для составления математической модели две переменные и построив затем графики соответствующих линейных уравнений.
На ветке сидело 

Ответ: синиц – _; воробьев – _.
Используя графический метод для каждой системы уравнений запишите число решений.
а) 
б)
Постройте график линейной функции 


А)
Б)
В)
Г)
Решения к заданиям для варианта 1
Правильный ответ: В
Правильный ответ: 1,9
Правильный ответ: –2
Правильный ответ: 3, 9
Правильный ответ: 0, 2
Правильный ответ: В
Видео:ОГЭ вариант-8 #5Скачать

Тест по темам «Уравнение», «Некоторые методы решения уравнений», «Графическое решение уравнений»
Вариант 2
Решите систему уравнений

графически и введите ответ.
Ответ:
x = __; y = __.
Постройте график функции 

Постройте график функции 


Используя графическую иллюстрацию, запишите решение уравнения 
Ответ: x = _ и x = _.
Решите уравнение и запишите его корень.
–3 • (4 + 3x) = (1 – 2x) • 4
Оцените каждый шаг решения данного уравнения следующим образом. Ставьте оценку «+», если шаг был выполнен правильно. Ставьте оценку «–», если шаг был выполнен ошибочно. После ошибочного шага дальше решение не оценивайте.
Раскроем скобки в обеих частях:

Перенесем переменные в левую часть, а числа в правую:

Упростим левую и правую части:

Запишем формулу для корня:

Вычислим и запишем корень:

Известно, что ордината некоторой точки прямой, являющейся графиком уравнения 

Ответ: абсцисса этой точки – __.

Установите соответствие между линейными уравнениями с двумя неизвестными и номерами графиков этих уравнений на рисунке.
Используя графический метод для каждой системы уравнений запишите число решений.
а) 
б)
Постройте график линейной функции 


А)
Б)
В)
Г)
Решения к заданиям для варианта 2
Правильный ответ: 1, 4
Правильный ответ: –16
Правильный ответ: –4
Правильный ответ: 2, 0
Правильный ответ: Б
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 925 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 684 человека из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 309 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Видео:ОГЭ 2022. Задание 11. Подробный разбор. Функция прямая. Как отличать.Скачать

Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 576 024 материала в базе
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Другие материалы
- 26.11.2021
- 253
- 6
- 26.11.2021
- 100
- 6
- 26.11.2021
- 99
- 0
- 26.11.2021
- 144
- 7
- 26.11.2021
- 70
- 0
- 26.11.2021
- 59
- 1
- 26.11.2021
- 128
- 1
- 26.11.2021
- 374
- 25
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 26.11.2021 89
- DOCX 445.3 кбайт
- 0 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Флока Диана Константиновна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 3 месяца
- Подписчики: 0
- Всего просмотров: 190179
- Всего материалов: 4697
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:№2Скачать
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Курганской области дистанционный режим для школьников продлили до конца февраля
Время чтения: 1 минута
Тринадцатилетняя школьница из Индии разработала приложение против буллинга
Время чтения: 1 минута
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Приемная кампания в вузах начнется 20 июня
Время чтения: 1 минута
ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек
Время чтения: 2 минуты
Онлайн-конференция о создании школьных служб примирения
Время чтения: 3 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Установите соответствие между графиками функций ... | ОГЭ 2017 | ЗАДАНИЕ 5 | ШКОЛА ПИФАГОРАСкачать
Урок алгебры в 8-м классе по теме «Графический способ решения уравнений»
Разделы: Математика
Всякое учение и всякое обучение основано на некотором уже ранее имеющемся знании.
Цели:
- обобщить и систематизировать свойства графиков некоторых функций, алгоритмы их построения;
- научить решать уравнения графическим способом, в частности используя возможности компьютерных программ;
- учить анализировать, выделять главное, сравнивать.
Формирование компетенций: компетенции самосовершенствования – саморегулирование и саморазвитие, речевое развитие (через устную и самостоятельную работу, формулировка выводов); компетенции социального взаимодействия – сотрудничество; компетенции в общении – устном, письменном; компетенции познавательной деятельности – постановка и решение познавательных задач, проблемные ситуации (их создание и разрешение), прогнозирование деятельности; компетенции информационных технологий – приём, переработка и выдача информации, компьютерная грамотность.
Тип урока: урок изучения нового материала.
Средства обучения: компьютер, медиапроектор, презентация (Приложение 1).
Формы организации учебной деятельности: индивидуальная, коллективная, диалог, работа с текстом слайда, работа в тетради, парная.
Методы: наглядный, словесный, графический (практический).
Методы мотивации: поощрение, порицание; создание проблемной ситуации, побуждение к поиску решения; предъявление учебных требований, прогнозирование будущей деятельности, самооценка деятельности; создание ситуации взаимопомощи, заинтересованность в результатах коллективной работы.
1. Оргмомент (1 мин.)
2. Актуализация знаний (12 мин.)
А). По карточкам (на доске):
№1. Решите уравнение 4х + 8 = –17 + 9х.
№2. Решите уравнение х 2 + х – 2 = 0.
№3. Решите уравнение х 2 = 
№4. Заполните таблицу:
| х | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| у = х 2 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
| х | -6 | -3 | -2 | -1 | 1 | 2 | 3 | 6 |
| у = | -1 | -2 | -3 | -6 | 6 | 3 | 2 | 1 |
(На этом этапе можно организовать взаимопроверку и взаимопомощь, если возникнет такая необходимость).
Б). Устная фронтальная работа. (Здесь и далее: подчёркивание – моменты управления презентацией)
Что называется функцией?
С какими функциями уже знакомы? (На партах – памятка, по которой учащиеся вспоминают связь между графиком и формулой, задающих функцию: Приложение 2).
Я предлагаю вашему вниманию формулы, задающие некоторые функции. Из этих функций нужно выбрать линейные. Но перед этим давайте вспомним определение линейной функции. (Работаем со слайдом 2).
Давайте вспомним, что является графиком (гиперссылка) линейной функции.
Среди выбранных нами линейных функций есть особенные. Что это за функции? Чем отличаются графики? (Разбейте линейные функции на две группы). (Работаем со слайдом 3).
Остались функции, о которых мы ничего ещё не сказали. Давайте дадим им название, и название их графикам. (Работаем со слайдом 4).
Что называется уравнением? Корнем уравнения? Что значит решить уравнение? Какие уравнения мы уже можем решать?
В) Проверяется работа по карточкам №1; №2; №3.
1) 4х + 8 = –17 + 9х,
4х – 9х = – 17 – 8,
– 5х = – 25,
х = 5.
Ответ: 5.
2) х 3 + х – 2 = 0,
D = в 3 – 4ас = 12 – 4 . 1 . (– 2) = 9 > 0, уравнение имеет два корня.
х1 = 1;
х2 = – 2.
Ответ: 1; – 2. (Могут решать по свойству корней: а + в + с = 0).
3) х 2 = 
х 3 = 6,
х 3 – 6 = 0. – Мы не располагаем никакими формулами для решения уравнений третьей степени. Как быть?
Значит, нужен другой способ решения таких уравнений. Как вы думаете, что это может быть за способ (исходя из устной работы). Одним из способов является графический способ. Записывается тема урока, (слайд 5).
Г). Давайте поставим цель урока. (Научиться решать уравнения с помощью графиков, слайд 6).
3. Изучение новой темы и первичное закрепление (15 мин.)
Мы получили уравнение х 3 – 6 = 0. Но строить график функции у = х 3 – 6 мы ещё не умеем. Т.е., что получается: это уравнение и графическим способом мы не можем решить? А может быть, нужно вернуться к первоначальному уравнению: х 2 = 

– Построить их графики.
– В одной координатной плоскости.
– Дальше найдём координаты точки пересечения.
– Нет, только значение х.
Итак, давайте ещё раз выработаем алгоритм решения уравнений графическим способом (каждый этап подтверждается показом в «Живой геометрии», Приложение 3). Используются результаты индивидуальной работы по заполнению таблицы (карточка №4). Учащиеся работают в тетрадях. Некоторые этапы в тетради записываются подробно, (слайд 7).
- Из уравнения выделяем знакомые нам функции.
- Строим графики функций в одной координатной плоскости.
- Находим координаты точек пересечения графиков.
- Из найденных координат выбираем значение абсциссы, т.е. х.
- Записываем ответ.
4. Физминутка (1 мин.)
5. Закрепление (5 мин.)
- Сколько корней имеет уравнение? (Гиперссылка – слайд 8, в «Живую геометрию», 3 страницы. Приложение 4). а)
б) х + 2 = х 2 ; в)
= х 2 .
- Попади в цель! (Слайд 9. Работа со слайдом показана на рисунке 1)
6. Домакшнее задание (слайд 10): (1 мин)
- п.26;
- № 623 (а), № 624(а);
- №4.10 на стр.117 (сборник Л.В.Кузнецовой): Наташа, Настя, Кирилл, Сергей.
7. Применение в образовательной области (1 мин)
Умения строить графики, читать графики, находить точки пересечения графиков нужны не только при изучении алгебры, но и при изучении физики, когда вы изучаете, н-р, зависимость плавления тела от температуры, зависимость скорости от времени движения двух тел. На уроках информатики, работая в электронных таблицах Excel, вы будете учиться строить графики, решать уравнения. На уроках химии скорость химических реакций также можно описать графически. Умение строить графики, диаграммы нужны и в повседневной жизни: для описания результатов голосования, удоя молока; в инженерных специальностях это умение очень важно.
8. Проверочная работа в виде теста (6 мин)
В – 1:
1. Какая из функций, приведённых ниже, является линейной:
а) у =
– 2; б) у = х – 2; в) у = х 2 – 2.
2. График функции у = 
а) прямой; б) гиперболой; в) параболой.
3. Установите соответствие между функциями и их графиками:
1) у =
; 2) у = 2х 2 ; 3) у = х – 2; 4) у = 2х.
А. Б. В. Г.
4. На рисунке 3 изображены графики функций у = х 3 и у = –2 х – 3. Используя графики, решите уравнение: х 3 = – 2х – 3.
В – 2:
1. Какая из функций, приведённых ниже, является линейной:
а) у =
+ 1; б) у =
+ 1; в) у = х 5 + 1.
2. График функции у = 3х 2 называется:
а) прямой; б) гиперболой; в) параболой.
3. Установите соответствие между функциями и их графиками:
1) у = –
; 2) у = х 2 – 1; 3) у = – х; 4) у = 1 – х.
А. Б. В. Г.
4. На рисунке 5 изображены графики функций у = – х 2 + 2 и у = 

Ответы:
В – 1: 1. б 2. б 3. 1 – Б; 2 – А; 3 – В; 4 – Г 4. б
В – 2: 1. а 2. в 3. 1 – В; 2 – Г; 3 – А; 4 – Б 4. а
9. Рефлексивно-оценочный этап (отвечают письменно в тетради после выполнения теста) (2 мин.) (Слайд 11)
а) за теоретический опрос;
б) за фронтальную работу;
в) за самостоятельную работу.
Видео:Установите соответствие между графиками функций ... | ОГЭ 2017 | ЗАДАНИЕ 5 | ШКОЛА ПИФАГОРАСкачать
Задания ОГЭ на анализ графиков
Начало
Если возникают вопросы — обращайтесь через форму для письма, рисунок конверта кликабелен.
Узнайте, как можно поддержать сайт и помочь его развитию.
- Изученные функции и их графики.
- Задания на соответствие графика и формулы функции в случае функций разных видов.
- Линейная функция. Прямая линия.
- Квадратичная функция. Парабола.
- Гипербола.
Видео:ОГЭ по математике. Задача 5-2Скачать

Изученные функции и их графики.
К концу учебного года в 9-ом классе вы успели изучить следующие функции:
(y = kx+b) — линейная функция. Графиком является прямая линия. Коэффициент (k) задаёт тангенс угла наклона к оси (Ox). Если (k>0), прямая наклонена под острым углом к оси, если (k (y = dfrac) График этой функции называется гиперболой. Его легко «узнать в лицо», потому что на данный момент это единственная хорошо изученная функция с разрывом. Так как на 0 делить нельзя, то график не может пройти через эту точку, иными словами, пересечь ось (Oy), поэтому состоит из двух отдельных ветвей. Коэффициент (k) показывает насколько далеко отстоят вершины ветвей гиперболы от начала координат, а знак коэффициента (знак перед дробью) показывает в каких четвертях расположены ветви гиперболы. Если (k>0), то в первой и третьей, если (k (y = ax^2+bx+c) — квадратичная функция. Графиком функции является парабола. Коэффициент (a) задаёт направление. Если (a>0), ветви параболы направлены вверх, если (a (y = sqrt) По внешнему виду этот график похож на повёрнутую на 90 градусов половинку параболы. Это, действительно, она и есть, потому что квадратный корень является обратной функцией для квадратичной функции. Влияние коэффициентов (a) и (b) на положение графика заметно, прежде всего, по его сдвигу вдоль оси (Ox). График должен быть расположен так, чтобы его область определения совпадала с ОДЗ выражения, т.е. (ax+b ge 0.)
Ещё подробнее повторить графики функций вы сможете, если перейдёте к сводной таблице и воспользуетесь помещенными там ссылками на другие статьи сайта и видео на youtube-канале Mathematichka.
Видео:Демо-вариант ОГЭ по математике, задача 5Скачать

Задания на соответствие графика и формулы функции.
Задачи, в которых приведены графики функций разных типов, я считаю самыми лёгкими в этом задании. Давайте рассмотрим несколько примеров, и вы в этом убедитесь.
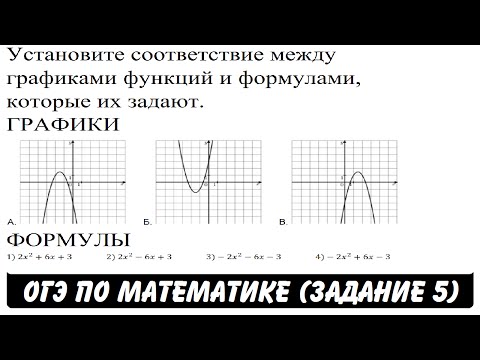
Задача 1. Установите соответствие между графиками функций и формулами, которые их задают
На рисунке всего один график прямая линия. Ищем среди формул ту, которая содержит (x) только в первой степени. Смотрим, чтобы в этой формуле не было квадрата и переменной в знаменателе. Такая формула только одна, это формула (3); y=-2x). Делаем вывод: графику Б) соответствует формула 3).
Среди формул только одна содержит (x^2) (формула 4), и только один график непрерывная кривая линия симметричная относительно вертикальной прямой, проведенной через её вершину. Это парабола – график В). Вывод: графику В) соответствует формула 4).
Остался один график с разрывом. Две отдельных ветви содержит график А) – гипербола. Но у нас две формулы с (x) в знаменателе. Придётся выбирать.
На графике А) ветви гиперболы расположены во второй и четвёртой координатных четвертях, где знаки координат (x и y) не совпадают, поэтому перед дробью в формуле гиперболы должен быть знак минус. Но оказалось, что этой приметы недостаточно, так как минус есть в обеих формулах.

Пусть (x = 1), тогда по формуле 1) получим (y = -dfrac = -4), а по формуле 2) получим (y = -dfrac = -2). Проводим на рисунке вертикальную линию (x = 1) до пересечения с графиком и смотрим значение (y). Получилось (y = -4), значит верна первая формула. Вывод: графику А) соответствует формула 1).
Ответ:
| А | Б | В |
| 1 | 3 | 4 |
Ответы и решения некоторых задач временно скрыты. Это задачи для самостоятельного решения. Чтобы посмотреть ответы, воспользуйтесь соответствующими кнопками. Но предварительно попробуйте решить задачу самостоятельно.
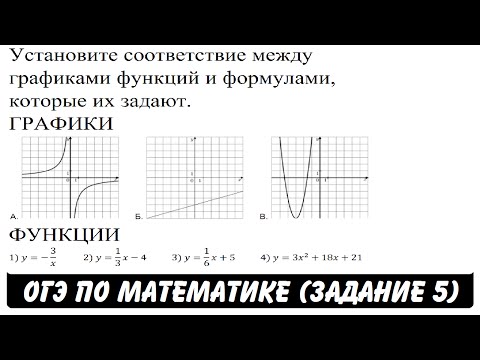
Задача 2. Установите соответствие между функциями и их графиками.
На графике 1) линия с разрывом, следовательно в формуле есть (x) в знаменателе. Вывод: графику 1) соответствует формула А).
На графике 2) изображена прямая линия. Осталась только одна формула, где (x) в первой степени умножен на число (dfrac = dfraccdot x). Вывод: графику 2) соответствует формула В).
Два оставшихся графика нелинейны, т.е. кривые линии. Формула Б) представляет собой квадратный трёхчлен. Следовательно, график должен быть параболой. Мы знаем, что парабола симметрична относительно линии, проходящей через вершину. График 3) обладает этим свойством, а на графике 4) такую линию провести невозможно. Вывод: формула Б) соответствует графику 3).
Замечение. Проверку ответа можно сделать «по единичке», т.е. задать какое-либо значение (x), подставить его в формулы, вычислить значения (y) и найти соответствующие точки на графике. Но решить задание в буквальном смысле по единичке, т.е. подставить (x = 1) в формулу Б), а затем найти на графиках 3) и 4) ординаты точек с абсциссой 1, не получится. Потому что во всех случаях будет (y = 2). Выбор не состоится.
Ответ:
| А | Б | В |
| 1 | 3 | 2 |
Задача 3. Установите соответствие между графиками функций и формулами, которые их задают.
Координатные плоскости здесь представлены без клеточек. Проверить принадлежность точек не получится, выбираем только по внешнему виду графиков.
Прямая линия олна – А). Её формула 1) содержит просто (x).
Симметричная кривая на графике В) – парабола. Формула 2) содержит (x^2).
На среднем графике кривая линия похожа на перевёрнутую половинку параболы. Это график функции 3) квадратный корень.
Ответ:
| А | Б | В |
| 1 | 3 | 2 |
Видео:8 класс, 21 урок, Графическое решение уравненийСкачать

Линейная функция. Прямая линия.
Задача 4. Установите соответствие между графиками функций и формулами, которые их задают.
Все графики – прямые линии и все формулы имеют вид (y = kx + b). Выбираем по наклону к оси (Ox) и точке пересечения с осью (Oy).
На графике В) прямая никак не наклонена к оси (Ox), она ей параллельна. Следовательно, угол наклона равен 0, тангенс угла наклона равен 0, угловой коэффициент (k=0), и (y = kx + b = 0cdot x + b = 0 + b = b.) Таким образом, формула, которая задаёт прямую, параллельную оси абсцисс, не должна содержать (x). Здесь такая формула под номером 3.
В двух оставшихся графиках наклон на глаз кажется примерно одинаковым. Поэтому начнём с точки пересечения с с осью (Oy). Вспомним, что для точек, расположенных на этой оси, (x=0), поэтому (y = kx + b = kcdot0 + b = 0 + b = b.) Таким образом, высота точки пересечения графика с этой осью показывает значение коэффициента (b) в формуле функции. На первом графике пересечение при (y=2), подходит формула (2); y = x+2.) На втором – при (y=0), подходит формула (1); y = 2x,) так как (2x = 2x+0.)
Сделаем проверку по единичке для графиков А) и Б).
При (x=1) по формуле 2) получим (y = 1 + 2 = 3). Если мы правильно установили соответствие, то точка с координатами (1;3) должна лежать на графике А).
При (x=1) по формуле 1) получим (y = 2cdot1 =2). Если мы правильно установили соответствие, то точка с координатами (1;2) должна лежать на графике Б).
Отметим эти точки на указанных графиках. Точки «не промахнулись», значит задача решена верно.
Ответ:
| А | Б | В |
| 2 | 1 | 3 |
Итак, все графики, которые задаются формулой (y = b), т.е. формулой, содержащей (y) и число, но не содержащей (x), представляют собой прямые линии, параллельные оси (Ox). Все графики, которые задаются формулой (y = kx), т.е. формулой, содержащей (x) в виде одночлена первой степени, представляют собой прямые линии, проходящие через начало координат. Эти выводы нужно запомнить на будущее не только, чтобы быстрее решать это задание ОГЭ, но и для задания на графики во второй части экзаменационного варианта.
Задача 5. Установите соответствие между функциями и их графиками.
Прямые на графиках 1) и 2) имеют одинаковый наклон. Одинаковый угловой коэффициент (k = 2) мы видим в формулах Б) и В). Методом исключения делаем вывод, что для графика 3) остаётся формула А).
Теперь, чтобы установить соответствие между графиками 1) и 2) и формулами Б) и В) смотрим на точку пересечения с осью (Oy). На первом графике она находится ниже оси абсцисс, что говорит о том, что в формуле коэффициент (b) имеет отрицательное значение. Смотрим: (b = -6) в формуле Б). Вывод: формула Б) соответствует графику 1), тогда формула В) соответствует графику 2).
Проверка по единичке: [А); y = -2cdot1+6 = 4;;; Б); y = 2cdot1-6 = -4;;; В); y = 2cdot1+6 = 8]
Как и предполагалось, (y = 4) на графике 3), (y = -4) на графике 1) (y = 8) на графике 2).
Ответ:
| А | Б | В |
| 3 | 1 | 2 |
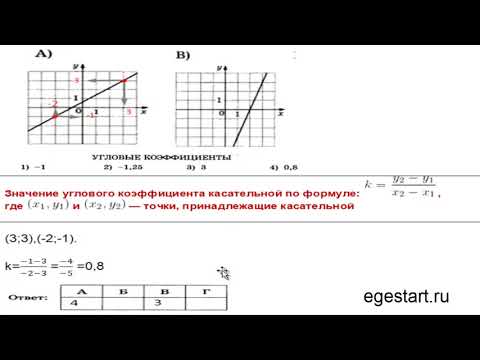
Задача 6. На рисунке изображены графики функций вида (y = kx+b.) Установите соответствие между графиками линейных функций и угловыми коэффициентами прямых.
[1); -1;;; 2); -1,25;;; 3); 3;;; 4);0,8] В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В | Г |
Угловой коэффициент равен тангенсу угла наклона прямой к оси (Ox.) На данный момент мы знаем, что тангенс определён в прямоугольном треугольнике, как отношение противолежащего катета к прилежащему. Поэтому, прежде всего, надо начертить прямоугольные треугольники такие, что их гипотенузы лежат на заданных прямых, а катеты проходят по клеточкам. Вершины этих треугольников обязательно должны находиться в узлах клеточек, иначе будет трудно определить длины катетов. Размер треугольника может быть произвольным, «приклеить» его к прямой можно в любом удобном месте.
Угол наклона прямой по определению отсчитывается от положительного направления оси абсцисс (оси (Ox)), поэтому в наших треугольниках противолежащий катет всегда параллелен оси (Oy) (считаем клеточки по вертикали), а прилежащий – оси (Ox) (считаем клеточки по горизонтали).
Если прямая образует с положительным направлением оси абсцисс тупой угол, то угловой коэффициент будет со знаком минус. Поскольку линии клеток параллельны, то можно смотреть угол между прямой и правой частью горизонтальных линий сетки, как показано на рисунке.
Итак, вычисляем угловые коэффициенты по чертежу
[А); k = frac = 0,8; ;;; Б); k = -frac = -1,25; ;;; В); k = frac = 3; ;;; Г); k = -frac = -1 ] и сравниваем с предложенными значениями. [1);-1;;; 2);-1,25;;; 3); 3 ;;; 4);0,8.]
Ответ:
| А | Б | В | Г |
| 4 | 2 | 3 | 1 |
На эту тему также можно посмотреть видеоуроки на странице Линейная функция или на youtube-канале Mathematichka.
📺 Видео
Графики функций. Задание №11 | Математика ОГЭ 2023 | УмскулСкачать

Как получить легкий балл на ОГЭ? / Подробный разбор заданий с графиками функций по математикеСкачать

Задание 10 Квадратичная функция Знаки коэффициентов а и сСкачать

[ОГЭ] На рисунках изображены графики функций вида у = кх + ЬСкачать
![[ОГЭ] На рисунках изображены графики функций вида у = кх + Ь](https://i.ytimg.com/vi/YiHEVLltWDk/0.jpg)
ГРАФИК ФУНКЦИИ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать
ОГЭ 2022. Математика. Задание 11. Подробный разбор. Квадратичная функция Как отличать.Скачать

Алгебра 8 класс (Урок№6 - Решение уравнений графическим способом.)Скачать

ОГЭ ДЛЯ НОЛИКОВ. ЗАДАНИЕ-11Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Алгебра 8 класс (Урок№19 - Уравнение х² = а.)Скачать

Все графики функций за 20 секундСкачать




















 б) х + 2 = х 2 ; в)
б) х + 2 = х 2 ; в)  = х 2 .
= х 2 .
 – 2; б) у = х – 2; в) у = х 2 – 2.
– 2; б) у = х – 2; в) у = х 2 – 2. ; 2) у = 2х 2 ; 3) у = х – 2; 4) у = 2х.
; 2) у = 2х 2 ; 3) у = х – 2; 4) у = 2х.

 + 1; б) у =
+ 1; б) у =  + 1; в) у = х 5 + 1.
+ 1; в) у = х 5 + 1.












