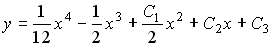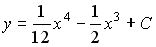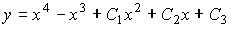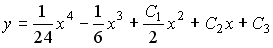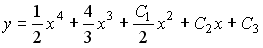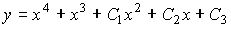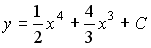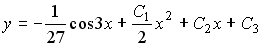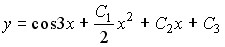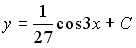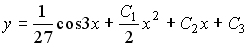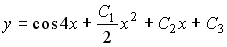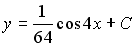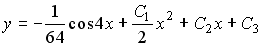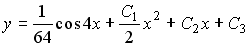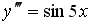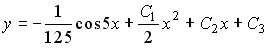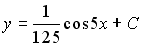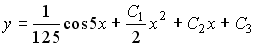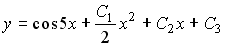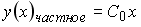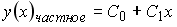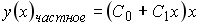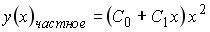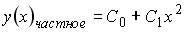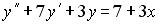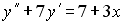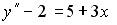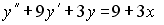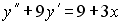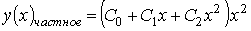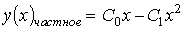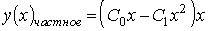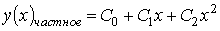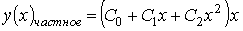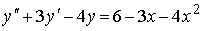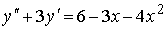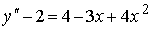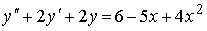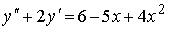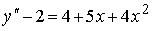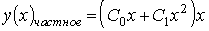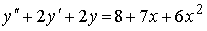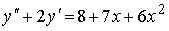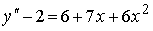4) линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами
Задание #118
Если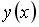 
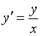
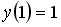
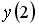
— решение уравнения 
, удовлетворяющее условию 
, тогда 
равно …
__________2_________________
Задание #119
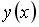
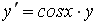
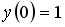
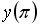
Если — решение уравнения 
, удовлетворяющее условию 
, тогда 
равно …
________1___________________
Задание #120
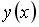
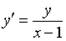
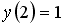
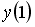
Если — решение уравнения 
, удовлетворяющее условию 
, тогда 
равно …
_________0__________________
Задание #121
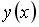
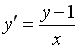
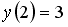
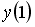
Если — решение уравнения 
, удовлетворяющее условию 
, тогда равно …
___________2________________
Задание #122
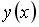
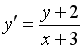
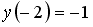
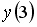
Если — решение уравнения 
, удовлетворяющее условию 
, тогда 
равно …
___________4________________
Задание #123
Общее решение дифференциального уравнения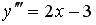 
имеет вид …
Выберите один из 4 вариантов ответа:
1) 
2) 
3) 
4) 
Задание #124
Общее решение дифференциального уравнения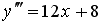 
имеет вид …
Выберите один из 4 вариантов ответа:
1) 
2) 
3) 
4) 
Задание #125
Общее решение дифференциального уравнения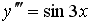 
имеет вид …
Выберите один из 4 вариантов ответа:
1) 
2) 
3) 
4) 
Задание #126
Общее решение дифференциального уравнения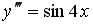 
имеет вид …
Выберите один из 4 вариантов ответа:
1) 
2) 
3) 
4) 
Задание #127
Общее решение дифференциального уравнения имеет вид … 
Выберите один из 4 вариантов ответа:
1) 
2) 
3) 
4) 
Задание #128
Установите соответствие между дифференциальным уравнением и общим видом его частного решения
Укажите соответствие для всех 3 вариантов ответа:
1) 
2) 
3) 
4) 
5) 
_2_ 
_3_ 
_4_ 
Задание #129
Установите соответствие между дифференциальным уравнением и общим видом его частного решения
Укажите соответствие для всех 3 вариантов ответа:
1)
2)
3)
4)
5)
_3_ 
_2_ 
_4_ 
Задание #130
Установите соответствие между дифференциальным уравнением и общим видом его частного решения …
Укажите соответствие для всех 3 вариантов ответа:
1) 
2) 
3) 
4) 
5) 
_4_ 
_5_ 
_1_ 
Задание #131
Установите соответствие между дифференциальным уравнением и общим видом его частного решения …
Укажите соответствие для всех 3 вариантов ответа:
1)
2)
3)
4)
5)
_2_ 
_1_ 
_5_ 
Задание #132
Установите соответствие между дифференциальным уравнением и общим видом его частного решения …
Укажите соответствие для всех 3 вариантов ответа:
1) 
2) 
3)
4)
5)
_3_ 
_4_ 
_5_ 
Задание #133
Бросают 2 монеты. События А — «цифра на первой монете» и В — «герб на второй монете» являются:
Выберите один из 4 вариантов ответа:
Видео:Общее и частное решение дифференциального уравненияСкачать
Учебно-методический комплекс «Математический анализ» (стр. 14 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
12.7 Если 
— решение уравнения 
, удовлетворяющее условию 
, тогда 
равно …
12.8 Если — решение уравнения 
, удовлетворяющее условию , тогда 
равно …
12.9 Если — решение уравнения 
, удовлетворяющее условию 
, тогда 
равно …
12.10 Если — решение уравнения 
, удовлетворяющее условию 
, тогда 
равно …
Дифференциальные уравнения высших порядков
13.1 Общее решение дифференциального уравнения 
имеет вид …
13.2 Общее решение дифференциального уравнения 
имеет вид …
13.3 Общее решение дифференциального уравнения 
имеет вид …
13.4 Общее решение дифференциального уравнения 
имеет вид …
13.5 Общее решение дифференциального уравнения 
имеет вид …
Линейные дифференциальные уравнения 2 порядка
14.1 Однородному дифференциальному уравнению второго порядка 
соответствует характеристическое уравнение …
14.2 Семейству интегральных кривых 
, где 
— произвольные постоянные, соответствует линейное однородное дифференциальное уравнение второго порядка …
14.3 Дано дифференциальное уравнение 
. Общим видом частного решения данного уравнения является …
14.4 Дано дифференциальное уравнение 
. Общим видом частного решения данного уравнения является …
14.5 Дано дифференциальное уравнение 
. Общим видом частного решения данного уравнения является …
14.6 Если функция 
имеет вид:
1. 
2. 
3. 
то частное решение 
неоднородного дифференциального уравнения 
следует искать в виде …
14.7 Если функция имеет вид:
1.
2. 
3. 
то частное решение неоднородного дифференциального уравнения 
следует искать в виде …
14.8 Установите соответствие между дифференциальным уравнением и общим видом его частного решения
1. 
2. 
3. 
14.9 Установите соответствие между дифференциальным уравнением и общим видом его частного решения
1. 
2. 
3. 
14.10 Установите соответствие между дифференциальным уравнением и общим видом его частного решения …
1. 
2. 
3. 
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать
Раздел 10. Источники
1.Никольский математического анализа. Том 1-2. М.: Наука, 2009г.
2.Кудрявцев курс математического анализа. М.: Наука, 2009г.
3.Кудрявцев математического анализа. Том 1-2. М.: Высш. школа, 2009г.
4. и др. Вся высшая математика. Тома 1-4. М.: Эдиториал 2009г.
5., Позняк математического анализа. Том 1-2. М Наука,2009.
6. Демидович задач и упражнений по математическому анализу. М.: Наука, 2008.
7. Высшая математика М. Высшее образование 2008г.
8.Фихтенгольц дифференциального и интегрального исчисления. Том 1-3. М.: Наука, 2007г.
9.Ефимов курс аналитической геометрии. М.: Высш. шк., 2007.г.
10.Гельфанд по линейной алгебре. М.: Высш. шк., 2006.
11.Шилов анализ (конечномерные линейные пространства). М.: Высш. шк., 2007.г.
12., Никольский уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. М.: Наука, 2009г.
13.Берман задач по курсу математического анализа. М.: Hаука, 2008г..
14. Э Дифференциальные уравнения и вариационное исчисление. М.: Высшая школа, 2008г.
15.Степанов дифференциальных уравнений. Гостехиздат. М.: 2007г..
16.Пискунов и интегральное исчисления: Т. 1-2.
Раздел 11 .Глоссарий
Абсолютной величиной (или модулем) действительного числа х называется само число х, если х неотрицательно, и противоположное число
х, если х отрицательно:
1 ‘ -х, если х 0, что |/(х)| 0 найдется такой номер N (зависящий от б, N = N(z)), что для всех членов последовательности с номерами п > N верно неравенство
А 0 найдется такое положительное число S > 0 (зависящее от s; S = S(s)), что для всех х, таких, что х> S, верно неравенство:
Ах)-А со, если ее предел равен нулю:
Функция f(x) называется бесконечно большой величиной при х -> х0, если для любого даже сколь угодно большого положительного числа М > 0 найдется такое положительное число 5 > 0 (зависящее от М, 8 = Ъ(М)), что для всех х, не равных д:0
и удовлетворяющих условию I x — х0 | М.
Функция /(х) называется непрерывной в точке х0, если она удовлетворяет следующим трем условиям: 1) определена в точке х0 (т. е. существует /(%)); 2) имеет конечный предел функции при х -> х0; 3) этот предел равен значению функции в точке х0, т. е.
Свойства функций, непрерывных на отрезке:
1. Если функция у = /(х) непрерывна на отрезке [а, Ь], то она ограничена на этом отрезке (см. рис. 6.10).
2. Если функция у = / (х) непрерывна на отрезке [а, Ь], то
она достигает на этом отрезке наименьшего значения т и наибольшего значения М теорема Вейерштрасса
Свойства функций, непрерывных на отрезке:
3. Если функция у = /(х) непрерывна на отрезке [а, Ь], то она ограничена на этом отрезке (см. рис. 6.10).
4. Если функция у = / (х) непрерывна на отрезке [а, Ь], то
она достигает на этом отрезке наименьшего значения т и наибольшего значения М теорема Вейерштрасса
Производной функции у = /(х) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):
геометрический смысл производной: производная /'(х0)есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой у=/(х) в точке х0,т. е. k=f'(x0).
Дифференциалом функции называется главная, линейная относительно Ах часть приращения функции, равная произведению производной на приращение независимой переменной
Функция F (х) называется первообразной функцией для функции f(x) на промежутке X, если в каждой точке х этого промежутка F'(x) =f(x).
Совокупность всех первообразных для функции /(х) на промежутке X называется неопределенным интегралом от
функции /(х) и обозначается jf(x)dx, где J — знак интеграла,
f(x) — подынтегршьная функция, f(x)dx — подынтегральное выражение. Таким образом,
Дифференциальным уравнением называется уравнение, связывающее искомую функцию одной или нескольких переменных, эти переменные и производные различных порядков данной функции.
Общим решением дифференциального уравнения я-го порядка называется такое его решение
которое является функцией переменной х и я произвольных независимых постоянных С,, С2. Сп. (Независимость постоянных означает отсутствие каких-либо соотношений между ними.)
частным решением дифференциального уравнения называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных Сх, С2. Сп.
Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид
Дифференциальное уравнение первого порядка называется однородным, если оно может быть представлено в виде
где g — некоторая функция (одной переменной).
Дифференциальное уравнение первого порядка называется линейным, если оно имеет вид
где /(х) и g (x) — некоторые (непрерывные) функции переменной х. В случае, когда функция g <x) тождественно равна нулю, уравнение называется однородным, в противном случае — неоднородным.
Числовым рядом называется бесконечная последовательность чисел щ, и2, . ип. соединенных знаком сложения:
Числа щ, и2. ип. называются членами ряда, а член ип —
общим или п-м членом ряда.
Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм
Свойства сходящихся рядов. 1. Если ряд щ+и2+. + ип+. сходится и имеет сумму S, то и ряд Хщ + Хи2 +. + Хип +. (полученный умножением данного ряда на число X) также сходится и имеет сумму XS.
2. Если ряды щ + и2 + • • • + ип + • • • и Vj + v2 +. + v„ +. сходятся
и их суммы соответственно равны Sy и S2, то и ряд
(И| + V,) + (и2 + v2) +. + (ип + vn) +. (представляющий сумму
данных рядов) также сходится, и его сумма равна 5, +S2.
Пусть имеется п переменных величин, и каждому набору их значений (х,, х2, . хп) из некоторого множества X соответствует одно вполне определенное значение переменной величины z. Тогда говорят, что задана функция нескольких переменных z = f(x<, . х„).
Линией уровня функции двух переменных z =f(x, у) называется множество точек на тоскости, таких, что во всех этих точках значение функции одно и то же и равно С.
Число А называется пределом функции z =f(x, у) при х -» х0 и у -*у0 (или в точке (х0, у0)), если для любого даже
сколь угодно малого положительного числа s > 0 найдется положительное число 5 > 0 (зависящее от е, 8 = 6(e)), такое, что для всех точек (х, у), отстоящих от точки (х0, у0) на расстояние р, меньшее, чем 81 (т. е. при 0 f(x, y)
Пусть точка (xQ, y0) — есть точка экстремума дифференцируемой функции z = fix,, у). Тогда частные производные fx(xQ, у0) и fy(xQ, уQ) в этой точке равны нулю.
Линии уровня функции полезности (они называются кривыми безразличия) (см. § 5.6) также позволяют рассматривать вопросы замещения одного товара другим и иллюстрировать решение задачи об оптимальном потреблении (потребительского выбора
Портфель ценных бумаг (под портфелем мы здесь будем понимать совокупность определенных ценных бумаг в определен-
ных количествах) характеризуется двумя основными параметрами — ожидаемой доходностью г и риском если частные производные и’х, и’у— функции полезности. Они называются предельными полезностями
Величина, обратная коэффициенту эластичности замещения, показывает приближенно, на сколько процентов изменится отношение предельных продуктов МР(х)/МР(у) при изменении отношения затрат ресурсов (х/у) на 1 %.
Приложение Лист переутверждения учебно-методического комплекса учебной дисциплины
одобрен на 2011/2012 учебный год. Протокол № 11 заседания кафедры
одобрен на 2012/2013 учебный год. Протокол № 11 заседания кафедры
одобрен на 2013/2014 учебный год. Протокол № 5 заседания кафедры
Видео:13. Как решить дифференциальное уравнение первого порядка?Скачать
Установите соответствие между дифференциальным уравнением и общим видом его частного решения
Дифференциальное уравнение y´+3xy=
является __________(каким?) дифференциальным уравнением первого порядка (вставить слово)
Общее решение линейного дифференциального уравнения
y´´+4y=0 имеет вид
Система дифференциальных уравнений
эквивалентна уравнению вида
Система дифференциальных уравнений
эквивалентна уравнению вида
В связи с дифференциальными уравнениями рассматривают ___ решения
В связи с дифференциальными уравнениями рассматривают ____ решения
График любого решения дифференциального уравнения называют______ (завершите определение словосочетанием)
Дано линейное однородное дифференциальное уравнение y´´–4y´+4y=0 Его общим решением является функция
Дано линейное однородное дифференциальное уравнение y´´–6y´+5y=0, тогда его общее решение имеет вид
Даны уравнения и . Укажите верные для них утверждения
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение является
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение является
Дифференциальное уравнение x2y´=x2+y2 является уравнением
Дифференциальное уравнение x3y´+x2y+2=0 является
Дифференциальное уравнение y´+xy=x3y2 является уравнением ___________ (укажите название)
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид:
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения характеристическое уравнение имеет вид
Для дифференциального уравнения = 0 характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Для системы характеристическое уравнение имеет вид
Завершите условие Уравнение вида будет однородным в том и только том случае, когда и являются однородными функциями _________ ( слово) порядка
Интегральная кривая дифференциального уравнения – это
Корни характеристическое уравнение есть
Нахождение функции , определенной на некотором интервале , имеющей на производную , такую, что для всех и удовлетворяющей условию , где и в точке определена функция , называется задачей
Общее решение дифференциального уравнения в областибудет функция
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения имеет вид
Общее решение дифференциального уравнения xy´´=y´ имеет вид
Общее решение линейного неоднородного дифференциального уравнения имеет вид
Общее решение линейного однородного дифференциального уравнения y´´–16y=0 имеет вид
Общее решение уравнения y´=e–2x имеет вид
Общее решение уравнения y´´+y=x+2 имеет вид
Общее решение уравнения y´´–y´=ex имеет вид
Общий интеграл дифференциального уравнения имеет вид
Общим решением линейного дифференциального уравнения y´´+9y=0 является функция
Общим решением системы дифференциальных уравнений , является
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Определитель Вронского для дифференциального уравнения равен
Порядок дифференциального уравнения – это неизвестной функции
При нахождении общего решения неоднородной системы линейных дифференциальных уравнений -го порядка используют
При решении линейных дифференциальных уравнений с постоянными коэффициентами используют
Рассмотрим уравнение Для этого уравнения верно:
Рассмотрим уравнение Для этого уравнения верно:
Рассмотрим уравнение Для этого уравнения верно:
Рассмотрим уравнение Для этого уравнения верно:
Рассмотрим уравнение Для этого уравнения верно:
Решение дифференциального уравнения второго порядка можно свести к решению дифференциального уравнения первого порядка в двух случаях Выберите их
Решить дифференциальное уравнение – это значит найти
Семейству линий сопоставьте огибающую
Семейству линий сопоставьте огибающую
Семейству линий сопоставьте огибающую
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполнена в области
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполнена в области
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполнена в области
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполняется в области
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполняется в области
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполнена в области
Теорема существования и единственности решения задачи Коши для дифференциального уравнения выполнена в области
Укажите верные для уравнений Клеро и Лагранжа утверждения
Укажите соответствие между типом дифференциального уравнения второго порядка и методом его решения
Укажите соответствия между дифференциальными уравнениями и их характеристическими уравнениями
Укажите соответствия между дифференциальными уравнениями и их частными решениями
Укажите соответствия между дифференциальными уравнениями и корнями их характеристических уравнений
Укажите соответствия между функциями и дифференциальными уравнениями
Укажите соответствия между функциями и дифференциальными уравнениями
Укажите утверждения верные для дифференциального уравнения Лагранжа
Укажите утверждения, верные для дифференциального уравнения Клеро
Установить зависимость вида общего решения дифференциального уравнения от корней соответствующего характеристического уравнения
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальным уравнением и его видом
Установить соответствие между дифференциальными уравнениями первого порядка и их названием
Установить соответствие между линейным однородным дифференциальным уравнением и видом его общего решения
Установить соответствие между линейным однородным дифференциальным уравнением и видом общего решения этого уравнения
Установить соответствие между линейным однородным дифференциальным уравнением и его характеристическим многочленом
Установить соответствие между линейными однородными дифференциальными уравнением и его общим решением
Установить соответствие между характеристическим многочленом и линейным однородным дифференциальным уравнением
Характеристическое уравнение дифференциального уравнения есть
Характеристическое уравнение дифференциального уравнения есть
Характеристическое уравнение дифференциального уравнения есть
Характеристическое уравнение дифференциального уравнения есть
Характеристическое уравнение дифференциального уравнения есть
Характеристическое уравнение дифференциального уравнения есть
Частное решение дифференциального уравнения есть
Частное решение дифференциального уравнения есть
Частное решение дифференциального уравнения есть
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение дифференциального уравнения имеет вид
Частное решение линейного неоднородного дифференциального уравнения второго порядка y´´+4y=ex имеет вид
Частное решение уравнения при есть
Частное решение уравнения при есть
📽️ Видео
Решение однородного дифференциального уравнения. Практическая часть. 11 класс.Скачать
Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать
Частное решение дифференциального уравнения. 11 класс.Скачать
Дифференциальные уравнения. 11 класс.Скачать
Видеоурок "Нахождение частных решений по виду правой части"Скачать
16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать
Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать
2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать
Дифференциальные уравнения с разделенными переменными. 11 класс.Скачать
Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать
Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать
Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать
ЛОДУ 2 порядка c постоянными коэффициентамиСкачать
Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать
ЛНДУ II п. со спец. правой ч. (sin, cos)Скачать
